Celebrating Soft Matter’s 10th Anniversary: Toward jamming by design
Heinrich M.
Jaeger
*
James Franck Institute and Department of Physics, The University of Chicago, 929 East 57th Street, Chicago, IL 60637, USA. E-mail: h-jaeger@uchicago.edu
First published on 20th October 2014
Abstract
In materials science, high performance is typically associated with regularity and order, while disorder and the presence of defects are assumed to lead to sub-optimal outcomes. This holds for traditional solids such as crystals as well as for many types of nanoscale devices. However, there are circumstances where disorder can be harnessed to achieve performance not possible with approaches based on regularity. Recent research has shown opportunities specifically for soft matter. There, the phenomenon of jamming leads to unique emergent behavior that enables disordered, amorphous systems to switch reversibly between solid-like rigidity and fluid-like plasticity. This makes it possible to envision materials that can change stiffness or even shape adaptively. We review some of the progress in this direction, discussing examples where jamming has been explored from micro to macro scales in colloidal systems, suspensions, granular-materials-enabled soft robotics, and architecture. We focus in particular on how the jammed aggregate state can be tailored by controlling particle level properties and discuss very recent ideas that provide an important first step toward actual design of specifically targeted jamming behavior.
Introduction
Jamming is the onset of rigidity in disordered, amorphous systems comprised of many constituent particles that interact via short-ranged repulsive forces. It is a cooperative phenomenon in which slight changes in local particle configuration and connectivity produce a system-spanning transformation of the mechanical properties. Jamming does not rely on temperature like ordinary phase transitions, but instead on local geometric constraints. It therefore applies to athermal systems far from thermodynamic equilibrium. As long as temperature is irrelevant, the key parameters characterizing jamming are the available free volume per particle and the applied shear stress. Jamming occurs when geometric constraints among neighboring particles prevent mobility and the applied stress is too small to cause yielding. Conversely, unjamming and the associated loss of aggregate rigidity occur when the free volume experienced by particles becomes large enough to allow for mobility or when a sufficiently large shear stress is applied to force the system to dilate and yield. An everyday example is a brick of vacuum-packed coffee, jammed into solid-like rigidity by the confining pressure exerted at the bounding interface. Simply removing the confinement by changing the boundary conditions at the interface, but without changing anything within the bulk, allows the material to dilate, unjam, and flow easily.Since jamming only depends on the degree to which particles block each other from rearranging inside a given volume, it does not require any particular particle size or type. There also is no major structural transition associated with jamming: the system is amorphous on either side of the transition. These two aspects have made jamming a candidate mechanism for glassy behavior observed in a wide range of often much more microscopic systems, including foams, colloids, and molecular glass formers.1–4 The jamming transition in macroscopic granular materials appears similarly subtle as far as a structural signature is concerned. At the same time, the change in dynamic response is dramatic: just as decreasing temperature near the glass transition drives up the viscosity by many orders of magnitude over a narrow temperature interval, in macroscopic granular systems changes of less than a percent in packing density suffice to turn a soft, malleable material into a rigidly jammed solid.5
Since its inception, the framework of a jamming phase transition has been used successfully to explain a multitude of behaviors associated with the rigidity onset in amorphous far-from-equilibrium materials, including their anomalous spectrum of normal modes, their dynamic heterogeneity, or their sensitivity to boundary and preparation conditions (for reviews see ref. 6–8). Building on this understanding, more recently a new direction has emerged that exploits jamming as a tool to design structural and dynamic properties of amorphous materials. The focus of this paper is to discuss some of the basic issues and to outline recent approaches toward jamming by design.
The main application appeal of a jamming transition is its ability to transform a material reversibly between flowing and rigid states. The fact that the material on both sides of the transition is highly disordered offers distinct advantages over ordinary crystalline solids in terms of the ability to withstand plastic deformation and dissipate energy, or to self-heal after impact and recover load bearing strength if suitably confined. If picked correctly, dry granular material can quickly and simply be poured or dumped into place, yet the resulting, amorphous particle aggregate is solid-like rigid, can support load and withstand shear. At the same time, a granular aggregate remains highly porous and permeable as well as reconfigurable. On large scales, these features are important, for example, for the construction and functioning of harbor breakwaters or jetties (Fig. 1a), for foundations, or for railroad beds. On smaller scales, they enable a range of unique applications for energy dissipation and vibration isolation, or as shape-adaptive, variable-compliance material.
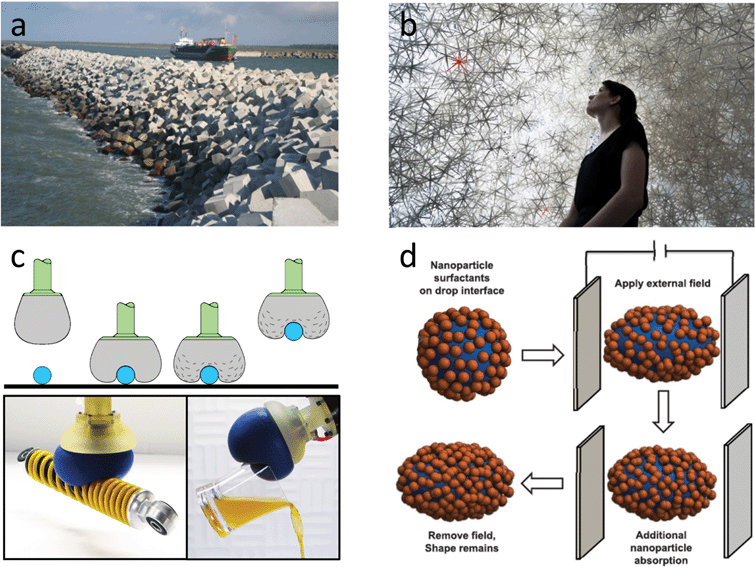 | ||
| Fig. 1 Jamming across a wide range of scales. (a and b) On large, architectural scales suitably shaped objects, jammed by pouring under gravity, stabilize breakwaters and enable domed spaces. Images with permission from BAM Infraconsult bv (a), and from K. Dierichs and A. Menges, ICD, Univ. Stuttgart (b). (c) Vacuum-jammed granular material inside an elastic membrane forms a universal gripper: the unjammed material conforms to the object's surface and establishes a close-fitting, rigid mould when jammed, enabling secure gripping (from left to right in the schematic). Images: switch from gripping heavy coil to fragile glass without needing active feedback. Adapted from ref. 5. (d) Jamming of nanoparticles on the surface of a liquid droplet, used to stabilize non-spherical drop shapes. From ref. 11, reprinted with permission from AAAS. | ||
In concentrated particle suspensions striking non-Newtonian flow behavior such as discontinuous shear thickening has recently been interpreted in terms of a granular jamming scenario,9,10 and the jamming of nanoparticles on the surface of liquid droplets has been used to stiffen the interface and enable non-equilibrium droplet shapes11 (Fig. 1d). Other recent applications have been in the area of soft robotics, including jamming-based robots,12 universal grippers5,13 (Fig. 1c) and flexible manipulators,14,15 tactile user interfaces,16 and new types of adaptive sockets for prostheses.17 In addition, there has been interest in jamming within the architecture and industrial design communities to create structures that can be rapidly deployable, widely changeable, and easily recyclable18–21 (Fig. 1b).
As these examples demonstrate, jamming has been enabling a wide range of applications, some older but many very new, and this is starting to forge connections between researchers and practitioners well beyond the usual realm of soft matter science. The important point to make, however, is that jamming applications so far have only started to explore the full range of possibilities. Much of the work has been limited to readily available particles and to the most basic forms of driving a system into the jammed state. The good news is that any aggregate of hard particles will jam eventually as its confinement is increased; but the bigger question is whether one can go beyond exploration and actually design for a specific target behavior, such as a given packing density for jamming to occur, a target yield stress for unjamming, or even a fully specified stress strain curve.
When we think of materials “by design”, we are envisioning a process that gets us from desired properties to requirements for the constituent components. Beyond its inherent difficulty, such a process for far-from-equilibrium systems constitutes a major intellectual challenge. The key reason is that now the target no longer is a thermodynamically favored ‘ground state.’ Instead, in a jammed material the aggregate behavior depends on the local connectivity and the ‘architecture’ of a contact network that is quenched into one of a myriad highly disordered, metastable configurations. Together with the wide range of possible particle shapes this allows for tremendous structural diversity and a very rich set of dynamic responses. Compared to regular lattice structures this also makes it significantly more challenging to predict how the overall, aggregate behavior is affected by the local, particle-level properties and packing arrangements.
Given these challenges, prior approaches have focused mainly on prediction or verification of aggregate behavior for ingredients that were given a priori, or on exploration by trial and error. Actual design, however, requires more: to develop and implement strategies that can tackle the inverse problem, namely to identify the microscale ingredients that will yield targeted macroscale outcomes (Fig. 2). In the science and engineering literature this is often termed ‘inverse design’, a misnomer that does not acknowledge the fact that true design by its very nature involves a top-down, macro to micro flow of considerations, starting from the desired end result.
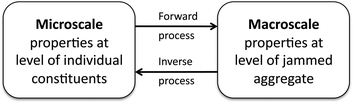 | ||
| Fig. 2 Jamming by design involves an inverse process that starts with macroscale target properties to identify microscale constituents. | ||
This review will first discuss some of the basic aspects of jamming insofar as they are relevant for applications and then show how jamming has enabled a range of innovative new approaches to create materials and structures that can adaptively change their stiffness or lock in a particular overall, macroscopic shape. Given that most of the jamming-enabled applications so far have used only the simplest of constituent particles, we next review recent results on tailoring the structural and dynamic properties of jammed systems by changing particle-level properties. This then leads to a discussion of a methodology for actual design and, beyond that, to how one can use the same methodology also for discovery of new material properties.
Jamming phase transition
In the limit where thermal energies are not important, the jamming transition is controlled by the average packing fraction ϕ and the applied shear stress τ. As the packing fraction is increased, and thereby the free volume per particle is decreased, there will be a critical density of particles at ϕJ such that a sufficiently large number of direct contacts among neighbors allow for mechanical stability of the aggregate as a whole, i.e., enable non-zero values for bulk and shear moduli; further increase in ϕ enables the aggregate to withstand larger shear stress before yielding and becoming unjammed (Fig. 3).6,7,22For frictionless, monodisperse spheres ϕJ corresponds to a packing density of ∼0.64 by volume, associated with amorphous configurations termed random close packing (RCP) or maximally random jammed packing (this is correct for infinite quench rates, and the precise value of ϕJ depends somewhat on how the packing is compressed into the jammed state23,24). With friction, mechanically stable sphere packings can exist in a range of packing densities extending to about 0.55, often called the random loose packing (RLP) limit, depending on the preparation procedure.25,26 Furthermore, by applying shear to initially fragile configurations in the regime between RLP and ϕJ, structural rearrangements inside the material build up a strong network of contact forces between neighboring particles, which spans the material and produces a robust shear jammed state (green region in Fig. 3, right panel) extending to ϕS.22,27,28
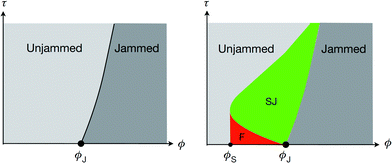 | ||
| Fig. 3 Jamming phase diagrams for frictionless (left) and frictional (right) systems. The two key parameters are the packing fraction ϕ and the applied shear stress τ. The shear-jammed region is labeled SJ; F denotes fragile configurations. From ref. 22, reprinted by permission from Macmillan Publishers Ltd. | ||
A simple way of appreciating the difference between the two jamming phase diagrams in Fig. 3 is to consider dilation. Frictionless spheres can be sheared past one another up to densities of ϕJ without requiring dilation. But for frictional particles to shear at ϕJ or slightly below, the system must dilate. The associated structural reorganization, and in particular the formation of force chains, causes the particles to jam against the confining boundaries as long as the overall volume is fixed. In this view, the onset of shear-induced rigidity emerges due to ‘frustrated dilation’. The width of the shear-jammed regime in Fig. 3 then depends on whether configurations exist below ϕJ that dilate upon shear. Note that this is not the same as asking only for mechanically stable configurations, which might simply collapse when sheared.26 The packing fraction ϕS where shear-jamming sets in therefore depends on both the frictional properties of the particles and their geometry. In the presence of attractive interactions or cohesion, mechanically stable packings can exist already at very low densities and ϕJ can decrease considerably.29,30
The onset of jamming as a function of packing density in the limit of vanishing shear, i.e., at ϕJ along the horizontal axis in Fig. 3, exhibits features that are reminiscent of phase transitions in thermodynamic systems, but at the same time differ in ways that make jamming unique.4,6,7 In particular, ϕJ plays the role of a critical point and quantities such as the bulk modulus, B, and the shear modulus, G, exhibit power law scaling with distance Δϕ = ϕ − ϕJ > 0 from the critical point. However, while G vanishes continuously as ϕJ is approached from above, B approaches a finite value and then drops discontinuously.
The resulting large ratio B/G in the marginally jammed state just above ϕJ signals that this state is much more susceptible to shear than to isotropic compression, behaving like a liquid in the limit that Δϕ approaches zero. Conversely, as Δϕ is increased and the aggregate is jammed more deeply, B/G decreases and the material behaves more like an ordinary solid also under shear, eventually exhibiting features similar to brittle solids, such as highly localized failure zones (shear bands).
The important point is that this wide range of response, all the way from liquid- to solid-like behavior, can be controlled without tuning any of the interactions among the constituent particles inside the bulk of the material. Instead, it can be controlled by the conditions at the outer, bounding surface, specifically by confining pressure (which sets Δϕ) and applied stress.
A couple remarks are in order. First, driving an unjammed system through the jamming transition and deep into the jammed state will lock in, or quench, a particular configuration. But before that happens and while the system is still traversing the marginally jammed regime, it responds to locally applied stresses in a highly nonlocal manner through an extended network of contact forces between neighboring particles, which in turn drive particle rearrangements. Adaptive response therefore needs to exploit this marginally jammed regime. Second, in many cases the non-negligible weight of individual particles implies that any aggregate at rest is going to be already in at least a lightly jammed state without need for further confinement, simply due to gravity (‘gravity jammed’). In this regard, dispersions of particles in a liquid, such as colloids or suspensions, offer the opportunity to start in the unjammed state at rest, as long as settling is prevented or can be ignored.
Jamming-based applications and devices
Soft robotics
There are a number of areas where new jamming-based applications have emerged. One of these is the field of soft robotics.12,31–35 Ordinary robots are largely made from hard components and materials that cannot change their physical form or change their compliance. In this context, jamming-enabled soft robotics provides a promising means to achieve special functionality.12,31The jamming transition itself does not do work and therefore cannot be used to induce movement. However, by using jamming to harden or soften certain parts of a robot selectively, one can activate degrees of freedom where needed. One of the first completely soft robots capable of moving and morphing was the JamBot,36 a grapefruit-size ‘soccer ball’, whose surface was segmented into roughly a dozen jammable cells, so that inflating or deflating the interior produced controlled shape changes (Fig. 4a–c). The fact that each JamBot cell was filled with granular material provided stiffness in the jammed state that goes well beyond what is possible with other soft, pneumatic robot systems.34,38,39
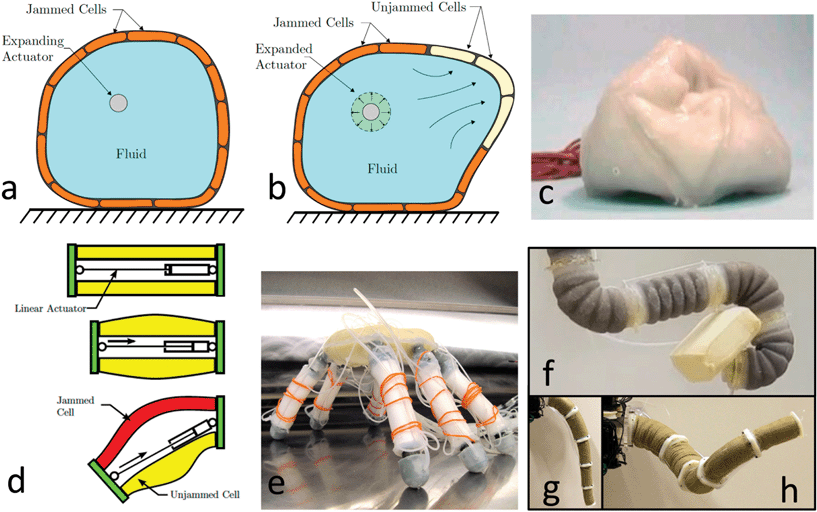 | ||
| Fig. 4 Jamming-based soft robotic systems. (a and b) Cross-sectional sketch of JamBot operation. From ref. 12. (c) JamBot in contracted state (evacuated interior).36 Image: frame from video.37 (d) Combination of linear actuator and jamming cells to add bending motion. From ref. 12. (e) Soft hexapod robot using one linear actuator plus four jamming cells as in (d) for each leg. Image: A. Mozeika, with permission. (f–h) Highly articulated manipulator, picking up a brick (f), unjammed (g), and jammed in corkscrew configuration (h). © 2012 IEEE. Reprinted with permission from ref. 15. | ||
While the jamming cells in a JamBot redirect the effect of volume change by a central actuator element, the same concept can also be used to redirect linear movement and thereby activate additional degrees of freedom. For example, surrounding a linear (McKibben-type) actuator with jamming cells can redirect the back-and-forth movement to add bending, thus turning one degree of freedom into three. This has been used to drive legged robots or enable locomotion of worm-type robots12 (Fig. 4d and e).
A second class of jamming-enabled robotic devices have been grippers and manipulators. In their simplest form, such grippers consist of an airtight elastic membrane filled with granular material (Fig. 1c). When pressed against an object in the unjammed state, the gripper easily conforms to the object's surface; jamming the gripper, for example by evacuating the air inside the membrane and thus strongly confining the granular material, then transforms it into a close-fitting mould that can pick up the object through a combination of friction, geometric interlocking and, for non-porous surfaces, suction.5,13,40 This type of gripper has the ability to pick up objects whose surfaces are very complex. In fact, it excels with surfaces that have protruding parts, a major difficulty for grippers using multi-fingered hands, mainly because manipulating the fingers appropriately involves a considerable amount of (visual or sensor-based) feedback and processing. By contrast, the jamming gripper can work in open-loop mode, i.e., without any feedback, and all ‘processing’ is done by the material itself. In other words, by driving the gripper through the jamming transition, the material self-adapts into the appropriate configuration, using its extremely large number of internal degrees of freedom.
Jamming grippers can easily handle unfamiliar, odd-shaped as well as fragile objects without reprogramming and therefore offer tremendous potential across a wide range of robotic operations where a large number of different objects have to be picked up and handled. Recent applications have included packing of consumer electronics,41 sorting of fresh fruit,42 or repositioning of obstacles on a locomotion test terrain.43 One potential vulnerability in applications might be the cut or puncture resistance of the elastic membrane, but recent work has shown how this can be resolved with advanced self-healing materials,44,45 an approach also used in the first commercially available jamming grippers.46
The fact that the stiffness of jamming-based systems can be changed over a wide range by varying the degree of confinement is advantageous in a number of other contexts as well. An innovative use of the gripper employs the device as an adaptive prosthesis socket.17 Here the variable compliance allows for automatic form fitting at low cost, an aspect particularly important when access to medical specialists is not available. Another application is as a compliance-adjustable foot sole for bipedal robots walking on uneven ground.47 Similar jamming technology has also found use in highly articulated manipulators. One of these has been an elephant-trunk-type system15 (Fig. 4f–h), while others are more focused on medical applications, such as endoscopes or flexible arms for minimally invasive surgery.14,48
Jamming-enabled controllable stiffness has recently also been employed for new types of tactile or haptic user interfaces. In these systems either the user manipulates a lightly jammed, malleable medium in order to input three-dimensional information, or the user's hands sense local deformations or stiffness changes of the medium, similar to reading Braille.16,49
Architecture
On large, architectural scales jamming has been utilized in two ways. First, vacuum jamming of granular media has been employed for creating large customized formwork (‘vacuumatics’).19–21 One particularly interesting application of this approach are reconfigurable, shapeable moulds for the casting of concrete into highly curved ‘free form’ shapes, with the added potential for easy surface texturing (Fig. 5a). Closely related are the ‘deflateables’,50 where the same concept of fabricating light-weight yet rigid structures by vacuum jamming was used for façade elements and even small bridges (Fig. 5c), with the difference being that the deflateables typically employed a regular lattice of constituent elements inside the airtight membrane. | ||
| Fig. 5 Jamming applications in architecture. (a) Freeform concrete casting fabricated with a vacuum-jammed mould (‘vacuumatics’19). Image: F. Huijben, TU Eindhoven, with permission. (b) Gravity-jammed dome structure made from ‘tumbling units’. From ref. 48. (c) Vacuum-jammed bridge (‘deflateables’50). Image: U. Knaack, TU Delft, with permission. (d) Robotic pouring of gravity-jammed wall structure (‘aggregate architecture’18). Image: K. Dierichs and A. Menges, ICD, Univ. Stuttgart, with permission. | ||
Second, jamming has been applied successfully to the construction of load-bearing structures formed by random assembly of interlocking particles that effectively self-confine and jam under gravity and thus do not require internal bonding or fasteners nor a confining membrane. One of the earliest to explore the resulting low-density, visually complex configurations for their architectural potential was Kentaro Tsubaki with his ‘tumbling units’ (Fig. 5b).51 This concept has been developed further into ‘aggregate architecture’ by Karola Dierichs and Achim Menges (Fig. 1b and 5d).18
The raw materiality of jammed granular aggregates, their inherent randomness coupled with their free-form potential, and the fact that these systems effectively compute their own stable configurations in response to applied (and potentially changing) mechanical loads, has led to much recent interest in the architecture community.52,53 In addition, since the constituent elements connect solely by interlocking and/or friction, such structures are not only formed and taken apart very quickly, but the particles can be recycled for immediate reuse. This also opens up intriguing possibilities for construction using robotic assembly18,54 (Fig. 5d).
Dynamic response and energy dissipation
So far we have discussed (quasi-)static jamming. A different class of applications exploits the unique dynamic response to rapidly applied loads. Jammed granular materials are excellent acoustic absorbers due to their highly porous and irregular structure in combination with dissipative, frictional particle interactions, and they are finding increased use for indoor as well as outdoor noise mitigation.55,56 In addition, jammed materials dampen structure-borne sound and vibrations, making them simple yet efficient “sound deadeners”.57,58The compression of an initially lightly jammed system by a piston or impacting object will lead to propagating densification fronts that behave like shocks and are highly effective in dissipating the impact energy. In 2D systems such shocks have been investigated numerically59–61 (Fig. 6a) and the associated evolution of the network of contact stresses can be imaged with single particle resolution using birefringence techniques62 (Fig. 6b–d). While the jammed network of particles takes up the majority of the stress in the process of undergoing rapid structural reconfigurations, the interstitial fluid, either a gas (air) or a liquid, can contribute significantly to the response. This happens when the permeability of the aggregate becomes small or when capillary effects induce significant confining stresses at the boundaries. Fig. 6e–f shows how this can affect the response to impact, a few milliseconds after a steel sphere (black) has been dropped onto a loosely packed bed of dry particles whose small diameter (50 μm) limits the air permeability.63,64 Since the interstitial gas cannot escape fast enough it works against any changes (expansion as well as contraction) in local void space. As a consequence, under ambient conditions the build-up of a large compaction front ahead of the sphere is avoided, enabling significant penetration beyond what is shown in the figure. By contrast, at reduced air pressure the impact into a jammed system of fine particles generates a dramatic front that quickly decelerates the sphere (Fig. 6f).63
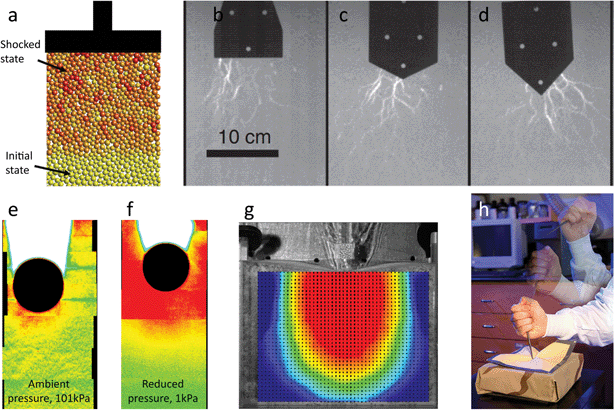 | ||
| Fig. 6 Dynamic response of jammed systems to rapidly applied loads. (a) Simulation of propagating 2D shock front when piston compresses lightly jammed initial state. Adapted from ref. 59. (b–d) Experimental visualization of dynamically reconfiguring networks of force chains, for three different impactor shapes, when a jammed 2D system of discs is impacted. Adapted from ref. 62. (e–f) Impact of steel sphere (12 mm diam.) into a 3D bed of frictional particles initially barely jammed (ϕ = 0.51, yellow-green color) imaged by high-speed X-ray imaging, 10 ms after impact. Compaction front (orange-red color) is much smaller when interstitial gas is present (101 kPa). Adapted from ref. 63. (g) Impact into quasi-2D layer of dense suspension. PIV overlay shows dynamically jammed region (orange-red) penetrating into initially unjammed region (blue). Adapted from ref. 68. (h) Kevlar fabric impregnated with dense suspension provides enhanced stab protection (‘liquid armor’). Images (a–d): reprinted with permission from ref. 59 and 62. © 2012, 2014 APS. Image (h) Univ. Delaware, UDel Research online magazine 2(2), with permission. | ||
Closely related are dynamic jamming fronts.65 These start on the unjammed side of the transition, i.e., in the ‘sonic vacuum’ where particles do not yet contact directly, and by compressing the system drive it into a jammed state. Jamming fronts have been observed in collisions of dense granular gas clusters66,67 and they can occur as well in dense suspensions of micron-sized particles in liquids.10,65,68,69 In all of these cases, impact at the free surface generates rapidly propagating fronts that transform fluid-like, unjammed material in front of them into solid-like, transiently jammed regions behind them (Fig. 6g). These impact-induced jammed regions can exert normal stresses sufficiently large to support the weight of grown persons running across deep pools filled with material that appears liquid at rest, such as ϕ ∼ 0.45 suspensions of cornstarch particles in water.10
Under steadily applied shear, dense suspensions (and also dry granular materials) can exhibit strongly non-Newtonian behavior whereby the shear stress increases nearly discontinuously by orders of magnitude beyond a critical shear rate. This so-called discontinuous shear thickening (DST) occurs at packing densities below ϕJ and is associated with frictional contacts among particles that establish a network capable of transmitting stresses from one shearing boundary to the other.9,10,70
DST differs from the jamming fronts in several ways. In particular, being a steady state phenomenon, it requires strongly confining boundaries, provided either by hard walls or the capillary (Laplace) pressure from particles protruding at a suspension–air interface.10,71 Without such confinement, the system will simply dilate. DST therefore has been associated with ‘frustrated dilation’.10 Alternatively, DST might be viewed as a dynamically reconfiguring shear-jammed state9 (however, any steady-state flow is necessarily beyond yielding and thus technically unjammed). Still, the key point is that the presence of an interstitial fluid introduces rate dependence, via the permeability of the aggregate and the viscosity of the fluid, as a new tunable parameter for both jamming fronts and DST.
For many applications, the difference between these two effects does not really matter as they likely occur in concert. For example, in ‘liquid armor’, a few layers of Kevlar fabric are impregnated with a dense suspension of hard particles72–74 (Fig. 6h), resulting in a personal protection system that is highly flexible under ordinary wearing conditions. When impacted or stabbed, it provides extraordinary puncture resistance due to quickly propagating jamming fronts in combination with DST in the interstices between the shearing fibers. Thick layers of suspension without fiber reinforcement, by contrast, will develop cracks if the impact exceeds the yield stress of the jammed solid.75
An important aspect of suspensions is that jamming can also be controlled by electric or magnetic fields. Similar to what happens during shear jamming, upon the application of an E- or B-field the particles in a suspension that was initially below ϕJ and unjammed are reorganized into a network of system-spanning, stress-bearing chains of induced dipoles. For low packing fractions this is simply a reinterpretation of the mechanism behind electro- or magneto-rheological (yield stress) fluids; however, more concentrated systems of this type, typically with ϕ > 0.3, behave very much like frictional or granular systems so that field-induced jamming may be the more appropriate scenario.76
Tailoring the jammed state at the particle level
In practically all of the applications just discussed, the link between the properties of the particles and that of the jammed aggregate was established by trial and error. As a first step toward jamming by design, i.e., achieving specific desired properties, it is therefore important to understand how jamming is affected by changes at the particle level.The behavior in the jammed state depends critically on the number and type of contacts between neighboring particles. This in turn is controlled by particle shape and particle properties such as their surface friction and their inherent elastic modulus. Shape-mediated particle interactions, in particular, lead to opportunities to generate jammed aggregates with special properties. At the same time, new technical capabilities have emerged, including 3D printing and non-invasive imaging techniques, which for the first time make experiments possible to investigate the role of particle shape systematically. This is particularly timely because of the recent computational progress in modeling packings of non-spherical particles.
Quite generally, the two aspects one might want to tune are the structural properties and the mechanical response. As we saw earlier, for random packings of spheres that are frictionless or that have been mechanically agitated to effectively mobilize friction, jamming occurs at ϕJ ∼ 0.64, while with friction, and depending on the preparation protocol, packings of purely repulsive spheres can be mechanically stable down to around 0.55.26 In order to tune the packing density at which jamming first sets in one can go beyond spheres, where there has been much recent progress concerning the maximum achievable packing densities in random aggregates, together with local particle configurations and correlations among neighboring particles.77 This includes particle shapes such as Archimedean and Platonic solids,78–83 ellipsoids, cuboids, or ‘superballs’,84–90 cylinders, cones, and frustums of different aspect ratios,90–92 as well as various types of particles constructed from overlapping disks or spheres.86,94–102
Properties such as the permeability and filtration capability of jammed particle aggregates depend not only on the average packing density but on the geometry of the local void space, in particular the network of ‘necks’ connecting the voids. This is a well-researched problem for sphere packings and various types of soil. On the other hand, less is known for jammed systems of shape-controlled non-spherical particles and the availability of such particles could open up new opportunities.
Similarly, detailed knowledge has been sparse concerning the mechanical response of packings of non-spherical particles, including sound propagation and heat transport, and with few exceptions the focus has been on particles with a convex shape. In the last few years, however, increasing attention has been paid to particles that are highly non-convex (or are sufficiently flexible so they can assume a concave shape during the packing process).89,103–112 Significant concavity allows for interlocking (‘geometrical friction’) or even entanglement. While non-convex particles with sharp bends or large protrusions tend to pack less densely than convex shapes, such interlocking can also enhance mechanical strength. This suggests that shapes could be found that optimize trade-offs between several desirable attributes of the jammed aggregate, such as maximized porosity together with high yield stress and/or high stiffness. However, general design rules to identify such shapes for amorphous packings do not exist yet (the next section discusses first approaches toward this goal).
As Fig. 7 shows, for given confining pressure, particle shape can indeed be used to tune and optimize the aggregate response within factors of two or three as far as properties like compressive modulus or yield stress are concerned.113 Still, simple shape variations do not produce dramatic changes in aggregate properties. This holds for convex shapes such as Platonic and Archimedean solids as well as non-convex shapes such as ‘jacks’ (hexapods with arms of various length) and ‘dolos’ (H-shaped with one side rotated 90 degrees), two particle types used in huge sizes for breakwaters103,114 (Fig. 1a). Furthermore, changes in confining pressure are seen to induce changes in relative performance among different shapes, i.e., there typically is no one shape that performs better in all situations. This highlights the complexity of the problem and the importance of accounting for preparation and boundary conditions when attempting to optimize.
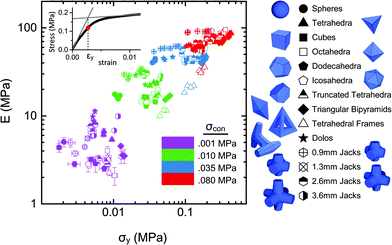 | ||
| Fig. 7 Relationship between compressive modulus E and yield stress σy in jammed aggregates, for 14 different particle shapes (symbols) and 4 confining pressures σcon (colors). Several independent measurements per shape and pressure are shown. Inset: extraction of yield stress from intersection of asymptotic behavior of stress–strain curves. Adapted from ref. 113. | ||
To the extent that the particle shapes used to compile Fig. 7 represent a sufficiently wide range of geometries, the data coverage defines a region of typical material response to applied compressive stress. We can now ask whether different particle types or shapes might allow us to reach not only further into the unpopulated areas of Fig. 7, but also discover qualitatively different behavior. For example, we know from work on granular chains, i.e., ‘granular polymers’ made from flexibly connected spheres, that entanglement can lead to significant self-confinement.108,110,115 As a result, already at very low applied confining pressure (a few kPa) chain aggregates can exhibit extremely high yield strengths (several MPa), far to the right of the data clusters shown in Fig. 7. Such aggregates will have a small modulus, but excel in terms of their low packing density (up to almost a factor two smaller than single particle aggregates105) and high toughness.
Designing the jammed state
Up to now we have been exploring properties of the jammed state for given constituent ingredients. As we discussed in the introduction, this is not the same as actual design, which by its very nature involves an inverse process: it starts from a desired performance goal for the jammed aggregate as a whole and then works backwards to identify the properties of the constituent ingredients required to reach that goal (Fig. 2). There are at least four reasons why this is difficult:• The first is that as the number of control parameters increases, the set of possible combinations grows exponentially. For jammed systems, even if aspects such as preparation and confining conditions as well as the particles' material and surface friction are fixed, shape alone is an essentially inexhaustible parameter.
• Second, especially for materials formed under non-equilibrium conditions, a critical additional aspect of design may be identifying the most appropriate boundary conditions and/or the processing path, including the initial conditions.
• Third, the mapping from the space of desired aggregate behaviors to the space of particle-level properties or processing conditions does not have to be unique. In other words, there can be a multitude of design solutions to a given design problem.
• Finally, to make a design-based solution valuable it should do more than represent a single answer to a single inverse problem. What we are looking for in a useful design is that it provides a path toward solving similar problems without having to go through the full inverse process. Ultimately we would like to obtain more general outcomes, termed here design rules, that apply to whole classes of related inverse problems.
Given this complexity in the absence of established design processes for jammed systems, simple trial and error clearly is not the best design strategy. And since several of the above issues apply very generally to the design of any complex system or material whether jamming-based or not, there has been considerable interest in developing automated, computer-based approaches to solving inverse problems of this type. A recent review of inverse methods for material design was written by Jain and coworkers.116
Finding input parameters that produce the desired output is a search and optimization problem. In high-dimensional search spaces and for very rugged (or very flat) underlying ‘search scapes’ gradient-based methods often have difficulties. To circumvent this, a powerful approach to such optimization instead unleashes a whole swarm, or ‘population,’ of trials, selects the best performing ones, mutates them and repeats the process, similar to evolution in biology. Over the last decade these methods have undergone major improvement and, for the type of optimization discussed here, their current champions are known as evolutionary strategies117,118.
Inverse methods using various types of artificial evolution have been applied to find crystal structures in materials made from atoms119,120 as well as colloids.121,122 They have been used to optimize organic photovoltaics123 or the stress–strain behavior parameters in alloys,124 for assembly planning of stochastically reconfigurable robotic systems,125 automatic design and manufacture of robotic life forms,126 as well as directed assembly of nanoscale patterns with thin films of block-copolymers.127–129
However, despite their potential, these methods have so far not been used much within the context of granular or jammed systems. Earlier exceptions include genetic design of particulate microstructure,130 identification of parameters in constitutive models,131 and the application of genetic algorithms for modeling concrete.132 Recently, more advanced evolutionary strategies have been applied to finding the appropriate shape of particles in random packings of compound particles comprised of bonded spheres (‘granular molecules’).133,134
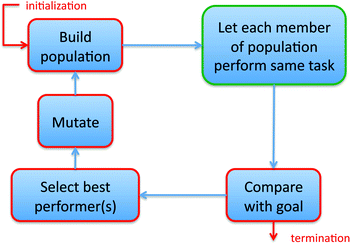
The basic architecture of an optimizer using evolutionary algorithms is shown in Fig. 8. It is a computational framework that provides input parameters for a large set (‘population’) of virtual experiments conducted in parallel via simulation, and improves the input over successive generations of virtual experiments until it reaches the targeted goal. Note that this process can proceed essentially in black-box fashion, with details about the underlying physics contained only in the engine that runs the virtual experiments (labeled ‘tasks’ in Fig. 8), each of them a standard ‘forward’ simulation. The only requirements are a metric to determine when the target has been reached, and a parameterization of the particle-scale properties that allows for appropriate mutations such that the next generation of input to the virtual experiments has a chance to explore the search space widely. In highly performing optimizers, such as the covariance matrix adaptation evolutionary strategy (CMA-ES),118 the selection of input for the next generation of trials is based on statistical sampling that starts with wide-ranging exploration and then homes in on promising regions.
A particular advantage of this approach is that initial and boundary conditions are automatically included as part of the forward simulations. As we saw in the last section, this is critically important when asking for optimal particle shapes, since those shapes are likely to change for different preparation conditions or confining pressures.
As a typical problem of this type, consider the question which particle shape forms the densest random packing when poured under gravity (for simplicity we limit ourselves to shapes that can be formed by bonding up to 10 spheres of arbitrary radii; Fig. 9). The shape identified by the optimizer depends strongly on the protocol: spheres for the case that the particles are frictional, and trimers for frictionless or vibrated packings.134 In the latter case, the trimers take advantage of statistical likelihoods for void spaces that can be filled by the two smaller ‘ears’ on each particle, an effect discovered and exploited by the optimizer without having been programmed in. On the other hand, the loosest packings are always formed by rod-like molecules (Fig. 9a).
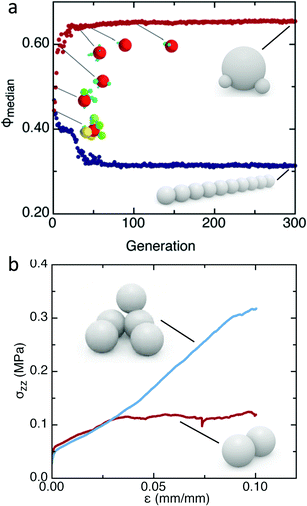 | ||
| Fig. 9 Particle shapes identified by evolutionary algorithm as optimal for given design task. (a) Find densest (top) and loosest (bottom) packing density when poured under gravity. Friction was assumed to be mobilized, corresponding to vibrating or tapping. The search process was started with a granular molecule containing 10 rigidly bonded spheres of random size and configuration. Adapted from ref. 134. (b) Find smallest granular molecule exhibiting strain stiffening in triaxial test. In this task, all spheres had the same size. For comparison, results from a packing comprised of dimers are shown in red. Adapted from ref. 133. | ||
The same evolutionary strategy has been applied successfully to finding shapes that lead to optimized dynamic properties, such as maximum stiffness or softness under compressive loading,133 and in principle could be tasked with optimizing any other aspect of the stress–strain curve, including design of specific failure behavior past yielding. Other aggregate properties that could be included in the design are permeability to liquid flow or energy absorption on impact. One can also easily imagine extending the method to include different types of interactions among contacting particles (e.g., local adhesion) or use other approaches besides bonded spheres for building up arbitrary particle shapes.
An important consequence is that the method can work with design targets that lie outside the envelope of known structural or dynamic behaviors. In other words, the optimizer can be used as a tool for discovery of new behavior. A first discovery of this type has been the smallest rigidly bonded granular molecule that, in aggregate, exhibits strain stiffening. The associated stress–strain curve with its increasing slope is not just quantitatively but qualitatively different from ordinary particulate matter, which weakens under compressive strain. The result is the remarkably asymmetric 5-sphere molecule shown in Fig. 9b, just large enough to interlock strongly.
While the optimizer delivers as final output one specific solution to one specific inverse problem, along the way it generates a myriad of trial solutions that can be thought of as solutions to related problems. However, there is no guarantee that the resulting mapping between problem space and solution space is smooth in the sense that small changes in desired target will result in small changes in the required particle-scale properties (in fact, in jammed systems, the large number of meta-stable configurations implies that shapes looking very differently can have almost identical packing density). A large set of individual solutions certainly is useful, but ideally we are looking for more generally valid design rules that allow us to interpolate smoothly in solution space.
One way to establish such rules is to use the optimizer to identify solutions to the extreme limits of a given class of target problems, such as the particle shapes that jam into the densest or the loosest configuration under given preparation conditions, and then devise a smooth interpolation in shape (this interpolation can be based on other considerations, such as ease of fabrication of the individual particles). As long as this interpolation meets the already identified extreme limits it is guaranteed to cover the full accessible parameter range in target parameter space. A proof of principle of this approach was recently demonstrated for the inverse packing problem.134
Outlook
Why would one want to use jamming, a process so inherently coupled to structural disorder, as a basis for the (rational) design of structures or materials? As this overview showed, jamming not only provides a means to transform matter quickly and reversibly from a fluid- into a solid-like state, but the resulting rigid structures can be robust and highly defect tolerant, reconfigurable and adaptive to external load changes.The wide range of jamming-enabled applications that recently have emerged is an indication of some of the unique opportunities for jamming by design. At the same time, actual design of jammed systems poses challenges that connect to forefront issues in materials science and are just beginning to be tackled, in particular the application of inverse methods to highly disordered systems far from equilibrium.
The topic of jamming by design originally came up in a discussion about the possibility of using fundamental insights from jamming to create amorphous aggregate materials with new kinds of properties. In this regard, inverse methods go beyond design and offer new possibilities for discovery. Of course, as with discovery by other means, inverse methods such as those based on evolutionary algorithms only can provide the evidence that a particular solution exists; they do not spell out why. Keeping this in mind, the evolutionary approach nevertheless has the potential to introduce a paradigm shift in the way the rational design of amorphous granular structures is approached.
The similarities in the dynamic behavior near the rigidity threshold discovered over the last several years among dry granular materials and dense suspensions or colloids strongly suggests that a jamming/unjamming scenario based on the local packing geometry and resulting particle connectivity might be applicable to wide classes of materials. At this stage, there are exciting opportunities to go beyond the current level of understanding, which has focused on the onset or demise of aggregate rigidity as a function of packing fraction, but left open many questions about the dynamic response to stress, in particular the loading-rate dependence of jamming. In granular systems such rate dependence emerges from the characteristic time scales associated with local particle rearrangement and/or deformations. In many dry granular materials, such rate dependence is thought to become important only for fast loading rates. As we saw, this is no longer the case when the flow of the interstitial fluid (gas or liquid) needs to be considered. Dense suspensions of particles therefore are a system in which it is possible to finely tune the rate of feedback between local microstructure changes and dynamics. This also opens up new possibilities by using non-Newtonian liquids as the interstitial medium, such as electro-rheological fluids, for further levels of control that allow for active feedback.
New capabilities to fabricate more complex particle shapes, via chemical synthesis, lithographic means or rapid 3D prototyping, have opened up the parameter space for design. For example, with template-based methods such as PRINT135 particles with dimensions from a few dozen nanometers to a few hundred microns can be fabricated in bulk quantities. Shape control provides an exciting path toward engineering specific, crystalline packing arrangements.136 Jamming exploits the same particle geometry to produce amorphous structures under conditions far from equilibrium. One area where this is likely to become increasingly important is additive manufacturing. Here, the need to deposit material rapidly often prevents careful, deliberate particle placement; yet a packing with tightly controlled particle contacts is required in order for the resulting aggregate to exhibit the desired strength after fusing or sintering.
The availability of optimized designed particles would make it possible to overcome a number of bottlenecks currently limiting the use of granular materials and open up new uses. This might include high-porosity high-toughness materials for medical implants that can be poured into place during minimal incision surgery, shock absorbing materials that have designed stress–strain characteristics to protect sensitive equipment, head-conforming helmet interiors for better impact protection, or particles designed for specific settling characteristics to minimize, or tune, compaction.
Going beyond the examples highlighted above, a very interesting direction is the use of inverse methods for optimizing the material processing path, such as the sequence of preparation steps for the jammed aggregate (including any initial agitation or compaction) or of applying boundary conditions (including confining pressure). In the simplest situation both the desired end result and the constituent ingredients are given, and the problem consists of finding the most efficient sequence of processing steps to reach the target. However, in many real world applications processing path and constituent properties are interdependent, and one would want to optimize both. Traditionally, such coupling has been difficult to take into account and we can expect large payoffs for automated inverse methods.
Given the computational power of inverse methods, more complex design goals are coming within reach, making it possible to optimize with respect to multiple, and possibly competing, goals. In architecture as well as for many engineering applications, an example might be to find the most porous yet stiffest structure under given boundary conditions. For soft robotics applications a goal might be to maximize the rigidity in the jammed state while minimizing it when unjammed.
Finally, while this review focused on macroscopic granular materials and (colloidal) suspensions as prototypical jammable systems, the issues are much broader. Similar behavior is observed in many other systems trapped in metastable configurations far from equilibrium, and similar questions apply about how to bias the selection of these metastable states such that the result approximates the desired behavior.
Acknowledgements
I would like to thank Sid Nagel for many discussions, including those that laid the foundation for this article, Sean Keller for introducing me to the work by several of the architects mentioned, Bob Behringer and Marc Miskin for feedback on drafts, and Kieran Murphy for invaluable help with finalizing the manuscript. Parts of this work were supported by the NSF through CBET-1334426 and through its MRSEC program via DMR-0820054, by ARO through W911NF-12-1-0182, as well as by the University of Chicago's Big Questions Incubator.References
- A. J. Liu and S. R. Nagel, Jamming is not just cool any more, Nature, 1998, 396, 21–22, DOI:10.1038/23819.
- M. E. Cates, J. P. Wittmer, J. P. Bouchaud and P. Claudin, Jamming, force chains, and fragile matter, Phys. Rev. Lett., 1998, 81, 1841–1844, DOI:10.1103/physrevlett.81.1841.
- A. J. Liu and S. R. Nagel, Jamming and rheology: constrained dynamics on microscopic and macroscopic scales, Taylor & Francis, London, 2001 Search PubMed.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Jamming at zero temperature and zero applied stress: the epitome of disorder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306, DOI:10.1103/physreve.68.011306.
- E. Brown, N. Rodenberg, J. Amend, A. Mozeika, E. Steltz, M. R. Zakin, H. Lipson and H. M. Jaeger, Universal robotic gripper based on the jamming of granular material, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18809–18814, DOI:10.1073/pnas.1003250107.
- A. J. Liu and S. R. Nagel, The Jamming Transition and the Marginally Jammed Solid, Annu. Rev. Condens. Matter Phys., 2010, 1, 347–369, DOI:10.1146/annurev-conmatphys-070909-104045.
- M. van Hecke, Jamming of soft particles: geometry, mechanics, scaling and isostaticity, J. Phys.: Condens. Matter, 2010, 22, 033101, DOI:10.1088/0953-8984/22/3/033101.
- C. Reichhardt and C. J. O. Reichhardt, Aspects of jamming in two-dimensional athermal frictionless systems, Soft Matter, 2014, 10, 2932–2944, 10.1039/c3sm53154f.
- R. Seto, R. Mari, J. F. Morris and M. M. Denn, Discontinuous shear thickening of frictional hard-sphere suspensions, Phys. Rev. Lett., 2013, 111, 218301, DOI:10.1103/physrevlett.111.218301.
- E. Brown and H. M. Jaeger, Shear thickening in concentrated suspensions: phenomenology, mechanisms, and relations to jamming, Rep. Prog. Phys., 2014, 77, 046602, DOI:10.1088/0034-4885/77/4/046602.
- M. M. Cui, T. Emrick and T. P. Russell, Stabilizing Liquid Drops in Nonequilibrium Shapes by the Interfacial Jamming of Nanoparticles, Science, 2013, 342, 460–463, DOI:10.1126/science.1242852.
- E. Steltz, A. Mozeika, J. Rembisz, N. Corson and H. M. Jaeger, Jamming as an Enabling Technology for Soft Robotics, Proc. SPIE 7642, Electroactive Polymer Actuators and Devices (EAPAD), 2010, p. 764225, DOI:10.1117/12.853182.
- J. R. Amend, E. M. Brown, N. Rodenberg, H. M. Jaeger and H. Lipson, A Positive Pressure Universal Gripper Based on the Jamming of Granular Material, IEEE Trans. Robot., 2012, 28, 341–350, DOI:10.1109/tro.2011.2171093.
- M. Cianchetti, T. Ranzani, i. Gerbon, T. Nanayakkara, K. Althoefer, P. Dasgupta and A. Menciassi, Soft Robotics Technologies to Address Shortcomings in Today's Minimally Invasive Surgery: The STIFF-FLOP Approach, Soft Robotics, 2014, 1, 122–131, DOI:10.1089/soro.2014.0001.
- N. Cheng, M. B. Lobovsky, S. J. Keating, A. M. Setapen, K. I. Gero, A. E. Hosoi, and K. D. Iagnemma, Design and Analysis of a Robust, Low-cost, Highly Articulated Manipulator Enabled by Jamming of Granular Media, in Proceedings of 2012 IEEE International Conference on Robotics and Automation (ICRA), St. Paul, Minnesota, 2012, pp. 4328–4333 DOI:10.1109/ICRA.2012.6225373.
- S. Follmer, D. Leithinger, A. Olwal, N. Cheng and H. Ishii, Jamming user interfaces: programmable particle stiffness and sensing for malleable and shape-changing devices, in Proceedings of the 25th annual ACM symposium on User interface software and technology, Cambridge, Massachusetts, USA, ACM, 2012, pp. 519–528 DOI:10.1145/2380116.2380181.
- E. Tsai, A. Hammond, and J. Hill, The BETH Project (Beneficial Technologies for Health): prosthetic socket for custom fit without custom fabrication, available at http://globalchallenge.mit.edu/teams/view/308, web page accessed Jan. 1, 2014.
- K. Dierichs and A. Menges, Aggregate Structures: Material and Machine Computation of Designed Granular Substances, Architect. Des., 2012, 82, 74–81, DOI:10.1002/ad.1382.
- F. Huijben and F. van Herwijnen, Vacuumatics; shaping space by "freezing" the geometry of structures, Proc. Int'l Conference on Tectonics: Making Meaning 2007, Eindhoven, The Netherlands, 2007, pp. 1–11 Search PubMed.
- F. Huijben and F. van Herwijnen, Vacuumatics: vacuumatically prestressed (adaptable) structures, in Proc. 6th International Conference on Computation of Shell and Spatial Structures IASS-IACM 2008 “Spanning Nano to Mega”, Cornell University, Ithaca, NY, ed. J. F. Abel and J. R. Cooke, Multi Science Publishing, Brentwood, UK, 2008 Search PubMed.
- F. Huijben, F. van Herwijnen and R. Nijsse, Vacuumatics 3D-Formwork Systems: Customised Free-Form Solidification, in Structural Membranes 2009 (International Conference on Textile Composites and Inflatable Structures), ed. E. Onate and B. Kröplin, Stuttgart, 2009, pp. 1–4 Search PubMed.
- D. Bi, J. Zhang, B. Chakraborty and R. P. Behringer, Jamming by Shear, Nature, 2011, 480, 355–358, DOI:10.1038/nature10667.
- P. Chaudhuri, L. Berthier and S. Sastry, Jamming Transitions in Amorphous Packings of Frictionless Spheres Occur over a Continuous Range of Volume Fractions, Phys. Rev. Lett., 2010, 104, 165701, DOI:10.1103/physrevlett.104.165701.
- M. P. Ciamarra, A. Coniglio and A. de Candia, Disordered jammed packings of frictionless spheres, Soft Matter, 2010, 6, 2975–2981, 10.1039/c001904f.
- G. Y. Onoda and E. G. Liniger, Random Loose Packings of Uniform Spheres and the Dilatancy Onset, Phys. Rev. Lett., 1990, 64, 2727–2730, DOI:10.1103/physrevlett.64.2727.
- M. Jerkins, M. Schröter, H. L. Swinney, T. J. Senden, M. Saadatfar and T. Aste, Onset of mechanical stability in random packings of frictional spheres, Phys. Rev. Lett., 2008, 101, 018301, DOI:10.1103/physrevlett.101.018301.
- S. Sarkar, D. P. Bi, J. Zhang, R. P. Behringer and B. Chakraborty, Origin of Rigidity in Dry Granular Solids, Phys. Rev. Lett., 2013, 111, 068301, DOI:10.1103/physrevlett.111.068301.
- M. Grob, C. Heussinger and A. Zippelius, Jamming of frictional particles: a nonequilibrium first-order phase transition, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 050201, DOI:10.1103/physreve.89.050201.
- G. Lois, J. Blawzdziewicz and C. S. O'Hern, Jamming transition and new percolation universality classes in particulate systems with attraction, Phys. Rev. Lett., 2008, 100, 028001, DOI:10.1103/physrevlett.100.028001.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Jamming phase diagram for attractive particles, Nature, 2001, 411, 772–775, DOI:10.1038/35081021.
- H. Lipson, Challenges and Opportunities for Design, Simulation, and Fabrication of Soft Robots, Soft Robotics, 2013, 1, 21–27, DOI:10.1089/soro.2013.0007.
- S. Kim, C. Laschi and B. Trimmer, Soft robotics: a bioinspired evolution in robotics, Trends Biotechnol., 2013, 31, 23–30, DOI:10.1016/j.tibtech.2013.03.002.
- D. Trivedi, C. D. Rahn, W. M. Kierb and I. D. Walker, Soft robotics: Biological inspiration, state of the art, and future research, Applied Bionics and Biomechanics, 2008, 5, 99–117, DOI:10.1080/11762320802557865.
- F. Ilievski, A. D. Mazzeo, R. E. Shepherd, X. Chen and G. M. Whitesides, Soft Robotics for Chemists, Angew. Chem., Int. Ed., 2011, 50, 1890–1895, DOI:10.1002/anie.201006464.
- C. Majidi, Soft Robotics: A Perspective—Current Trends and Prospects for the Future, Soft Robotics, 2013, 1, 5–11, DOI:10.1089/soro.2013.0001.
- E. Steltz, A. Mozeika, N. Rodenberg, E. Brown and H. M. Jaeger, JSEL: Jamming Skin Enabled Locomotion, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2009), 2009, pp. 5672–5677, DOI:10.1109/Iros.2009.5354790.
- http://youtu.be/SbqHERKdlK8, available at web page accessed 30/10/2014.
- R. F. Shepherd, F. Ilievski, W. Choi, S. A. Morin, A. A. Stokes, A. D. Mazzeo, X. Chen, M. Wang and G. M. Whitesides, Multigait soft robot, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20400–20403, DOI:10.1073/pnas.1116564108.
- S. A. Morin, R. F. Shepherd, S. W. Kwok, A. A. Stokes, A. Nemiroski and G. M. Whitesides, Camouflage and Display for Soft Machines, Science, 2012, 337, 828–832, DOI:10.1126/science.1222149.
- Y. Jiang, J. R. Amend, H. Lipson and A. Saxena, Learning hardware agnostic grasps for a universal jamming gripper, in IEEE International Conference on Robotics and Automation (ICRA) 2012, IEEE, 2012, pp. 2385–2391 DOI:10.1109/ICRA.2012.6225049.
- M. Rooker, A. Angerer, J. Capco, C. Heindl, A. Olarra, E. Fuentes, C. Wögerer, and A. Pichler, Flexible Grasping of Electronic Consumer Goods, in Robotics in Smart Manufacturing (Proc. Int. Workshop WRSM 2013 & FAIM 2013), Springer Verlag, Berlin, 2013, pp. 158–169 DOI:10.1007/978-3-642-39223-8_15.
- C. Blanes, M. Mellado, C. Ortiz and A. Valera, Technologies for robot grippers in pick and place operations for fresh fruits and vegetables, Spanish. J. Agr. Res., 2011, 9, 1130–1141, DOI:10.5424/sjar/20110904-501-10.
- F. Qian, K. Daffon, T. Zhang and D. I. Goldman, An Automated System for Systematic Testing of Locomotion on Heterogeneous Granular Media, in Nature-Inspired Mobile Robotics: 16th Int. Conf. on Climbing and Walking Robots and the Support Technologies for Mobile Machines (CLAWAR 2013, Sydney, Australia), ed. K. J. Waldron, M. O. Tokhi and G. S. Virk, World Scientific, Singapore, 2013, pp. 547–554, DOI:10.1142/9789814525534_0069.
- R. F. Shepherd, A. A. Stokes, R. M. D. Nunes and G. M. Whitesides, Soft Machines that are Resistant to Puncture, and that Self Seal, Adv. Mater., 2013, 25, 6709–6713, DOI:10.1002/adma.201303175.
- N. G. Cheng, A. Gopinath, L. Wang, K. Iagnemma and A. E. Hosoi, Thermally tunable, Self-healing composites for soft robotic applications, Macromol. Mater. Eng., 2014, 299, 1279–1284, DOI:10.1002/mame.201400017.
- http://www.empirerobotics.com, available at web page accessed 30/10/2014.
- A. Najmuddin, Y. Fukuoka and S. Ochiai, Experimental development of stiffness adjustable foot sole for use by bipedal robots walking on uneven terrain, in 2012 IEEE/SICE International Symposium on System Integration (SII), IEEE, 2012, pp. 248–253 DOI:10.1109/SII.2012.6426940.
- A. J. Loeve, O. S. van de Ven, J. G. Vogel, P. Breedveld and J. Dankelman, Vacuum packed particles as flexible endoscope guides with controllable rigidity, Granular Matter, 2010, 12, 543–554, DOI:10.1007/s10035-010-0193-8.
- A. A. Stanley, J. C. Gwilliam, and A. M. Okamura, Haptic Jamming: A Deformable Geometry, Variable Stiffness Tactile Display using Pneumatics and Particle Jamming, in IEEE World Haptics Conference (Daejeon, Korea, 2013), IEEE, 2013, pp. 25–30 DOI:10.1109/WHC.2013.6548379.
- U. Knaack, T. Klein and M. Bilow, Deflateables/Imagine 02, 010 Publishers, Rotterdam, The Netherlands, 2008 Search PubMed.
- K. Tsubaki, in Matter: Material Processes in Architectural Production, ed. G. P. Borden and M. Meredith, Routledge Press, Taylor & Francis Books, London, 2011, pp. 187–203 Search PubMed.
- P. Ball, Material Witness Material Computation, Nat. Mater., 2012, 11, 362, DOI:10.1038/nmat3321.
- A. Menges, Material Computation: Higher Integration in Morphogenetic Design Introduction, Architect. Des., 2012, 82, 14–21, DOI:10.1002/ad.1374.
- F. Gramazio and M. Kohler, Made by Robots: Challenging Architecture at the Large Scale, Architect. Des., 2014, 84 DOI:978-1-118-53548-6.
- N. N. Voronina and K. V. Horoshenkov, A new empirical model for the acoustic properties of loose granular media, Appl. Acoust., 2003, 64, 415–432, DOI:10.1016/s0003-682x(02)00105-6.
- T. Brunet, X. Jia and P. Mills, Mechanisms for acoustic absorption in dry and weakly wet granular media, Phys. Rev. Lett., 2008, 101, 138001, DOI:10.1103/physrevlett.101.138001.
- C.-J. Hsu, D. L. Johnson, R. A. Ingale, J. J. Valenza, N. Gland and H. A. Makse, Dynamic Effective Mass of Granular Media, Phys. Rev. Lett., 2009, 102, 058001, DOI:10.1103/physrevlett.102.058001.
- J. Valenza, C.-J. Hsu, R. Ingale, N. Gland, H. A. Makse and D. L. Johnson, Dynamic effective mass of granular media and the attenuation of structure-borne sound, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 051304, DOI:10.1103/physreve.80.051304.
- L. R. Gomez, A. M. Turner, M. van Hecke and V. Vitelli, Shocks near jamming, Phys. Rev. Lett., 2012, 108, 058001, DOI:10.1103/physrevlett.108.058001.
- L. R. Gomez, A. M. Turner and V. Vitelli, Uniform shock waves in disordered granular matter, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041302, DOI:10.1103/physreve.86.041302.
- S. Ulrich, N. Upadhyaya, B. van Opheusden and V. Vitelli, Shear shocks in fragile networks, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20929–20934, DOI:10.1073/pnas.1314468110.
- A. H. Clark, A. J. Petersen and R. P. Behringer, Collisional model for granular impact dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012201, DOI:10.1103/physreve.89.012201.
- J. R. Royer, B. Conyers, E. I. Corwin, P. J. Eng and H. M. Jaeger, The role of interstitial gas in determining the impact response of granular beds, Europhys. Lett., 2011, 93, 28008, DOI:10.1209/0295-5075/93/28008.
- J. R. Royer, E. I. Corwin, P. J. Eng and H. M. Jaeger, Gas-mediated impact dynamics in fine-grained granular materials, Phys. Rev. Lett., 2007, 99, 038003, DOI:10.1103/Physrevlett.99.038003.
- S. R. Waitukaitis, L. K. Roth, V. Vitelli and H. M. Jaeger, Dynamic jamming fronts, Europhys. Lett., 2013, 102, 44001, DOI:10.1209/0295-5075/102/44001.
- J. C. Burton, P. Y. Lu and S. R. Nagel, Energy Loss at Propagating Jamming Fronts in Granular Gas Clusters, Phys. Rev. Lett., 2013, 111, 188001, DOI:10.1103/physrevlett.111.188001.
- J. C. Burton, P. Y. Lu and S. R. Nagel, Collision Dynamics of Particle Clusters in a Two-dimensional Granular Gas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062204, DOI:10.1103/physreve.88.062204.
- I. R. Peters and H. M. Jaeger, Quasi-2D dynamic jamming in cornstarch suspensions: visualization and force measurements, Soft Matter, 2014, 10, 6564–6570, 10.1039/c4sm00864b.
- S. R. Waitukaitis and H. M. Jaeger, Impact-activated solidification of dense suspensions via dynamic jamming fronts, Nature, 2012, 487, 205–209, DOI:10.1038/nature11187.
- N. Fernandez, R. Mani, D. Rinaldi, D. Kadau, M. Mosquet, H. Lombois-Burger, J. Cayer-Barrioz, H. J. Herrmann, N. D. Spencer and L. Isa, Microscopic mechanism for the shear-thickening of non-Brownian suspensions, Phys. Rev. Lett., 2013, 111, 108301, DOI:10.1103/physrevlett.111.108301.
- A. Fall, F. Bertrand, G. Ovarlez and D. Bonn, Yield stress and shear banding in granular suspensions, Phys. Rev. Lett., 2009, 103, 178301, DOI:10.1103/physrevlett.103.178301.
- D. P. Kalman, R. L. Merrill, N. J. Wagner and E. D. Wetzel, Effect of Particle Hardness on the Penetration Behavior of Fabrics Intercalated with Dry Particles and Concentrated Particle-Fluid Suspensions, ACS Appl. Mater. Interfaces, 2009, 1, 2602–2612, DOI:10.1021/am900516w.
- A. Srivastava, A. Majumdar and B. S. Butola, Improving the impact resistance performance of Kevlar fabrics using silica based shear thickening fluid, Mater. Sci. Eng., A, 2011, 529, 224–229, DOI:10.1016/j.msea.2011.09.021.
- J. L. Park, B. I. Yoon, J. G. Paik and T. J. Kang, Ballistic performance of p-aramid fabrics impregnated with shear thickening fluid; Part II - Effect of fabric count and shot location, Text. Res. J., 2012, 82, 542–557, DOI:10.1177/0040517511420765.
- M. Roché, E. Myftiu, M. C. Johnston, P. Kim and H. A. Stone, Dynamic Fracture of Nonglassy Suspensions, Phys. Rev. Lett., 2013, 110, 148304, DOI:10.1103/PhysRevLett.110.148304.
- C. S. Orellana, J. He and H. M. Jaeger, Electrorheological response of dense strontium titanyl oxalate suspensions, Soft Matter, 2011, 7, 8023–8029, 10.1039/c1sm05565h.
- A. Baule and H. A. Makse, Fundamental challenges in packing problems: from spherical to non-spherical particles, Soft Matter, 2014, 10, 4423–4429, 10.1039/c3sm52783b.
- F. Y. Fraige, P. A. Langston and G. Z. Chen, Distinct element modelling of cubic particle packing and flow, Powder Technol., 2008, 186, 224–240, DOI:10.1016/j.powtec.2007.12.009.
- A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray and S. C. Glotzer, Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra, Nature, 2009, 462, 773–777, DOI:10.1038/nature08641.
- S. Torquato and Y. Jiao, Dense packings of the Platonic and Archimedean solids, Nature, 2009, 460, 876–879, DOI:10.1038/Nature08239.
- A. Jaoshvili, A. Esakia, M. Porrati and P. M. Chaikin, Experiments on the random packing of tetrahedral dice, Phys. Rev. Lett., 2010, 104, 185501, DOI:10.1103/PhysRevLett.104.185501.
- J. Baker and A. Kudrolli, Maximum and minimum stable random packings of Platonic solids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 061304, DOI:10.1103/physreve.82.061304.
- M. Neudecker, S. Ulrich, S. Herminghaus and M. Schröter, Jammed Frictional Tetrahedra are Hyperstatic, Phys. Rev. Lett., 2013, 111, 028001, DOI:10.1103/physrevlett.111.028001.
- P. W. Cleary and M. L. Sawley, DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge, Appl. Math. Model., 2002, 26, 89–111, DOI:10.1016/s0307-904x(01)00050-6.
- A. Donev, R. Connelly, F. H. Stillinger and S. Torquato, Underconstrained jammed packings of nonspherical hard particles: Ellipses and ellipsoids, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051304, DOI:10.1103/physreve.75.051304.
- C. F. Schreck, N. Xu and C. S. O'Hern, A comparison of jamming behavior in systems composed of dimer- and ellipse-shaped particles, Soft Matter, 2010, 6, 2960–2969, 10.1039/c001085e.
- G. W. Delaney and P. W. Cleary, The packing properties of superellipsoids, Europhys. Lett., 2010, 89, 34002, DOI:10.1209/0295-5075/89/34002.
- R. F. Shepherd, J. C. Conrad, T. Sabuwala, G. G. Gioia and J. A. Lewis, Structural evolution of cuboidal granular media, Soft Matter, 2012, 8, 4795–4801, 10.1039/c2sm06829j.
- S. Torquato and Y. Jiao, Organizing principles for dense packings of nonspherical hard particles: Not all shapes are created equal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 011102, DOI:10.1103/physreve.86.011102.
- R. Ni, A. P. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Phase diagram of colloidal hard superballs: from cubes via spheres to octahedra, Soft Matter, 2012, 8, 8826–8834, 10.1039/C2sm25813g.
- A. Wouterse, S. R. Williams and A. P. Philipse, Effect of particle shape on the density and microstructure of random packings, J. Phys.: Condens. Matter, 2007, 19, 406215, DOI:10.1088/0953-8984/19/40/406215.
- A. Wouterse, S. Luding and A. P. Philipse, On contact numbers in random rod packings, Granular Matter, 2009, 11, 169–177, DOI:10.1007/s10035-009-0126-6.
- J. Zhao, S. X. Li, P. Lu, L. Y. Meng, T. Li and H. P. Zhu, Shape influences on the packing density of frustums, Powder Technol., 2011, 214, 500–505, DOI:10.1016/j.powtec.2011.09.013.
- D. O. Potyondy and P. A. Cundall, A bonded-particle model for rock, Int. J. Rock Mech. Min. Sci., 2004, 41, 1329–1364, DOI:10.1016/j.ijrmms.2004.09.011.
- T. Pöschel and T. Schwager, Computational granular dynamics: models and algorithms, Springer-Verlag, Berlin, 2005 Search PubMed.
- D. O. Potyondy, Simulating stress corrosion with a bonded-particle model for rock, Int. J. Rock Mech. Min. Sci., 2007, 44, 677–691, DOI:10.1016/j.ijrmms.2006.10.002.
- M. Kodam, R. Bharadwaj, J. Curtis, B. Hancock and C. Wassgren, Force model considerations for glued-sphere discrete element method simulations, Chem. Eng. Sci., 2009, 64, 3466–3475, DOI:10.1016/j.ces.2009.04.025.
- C. Salot, P. Gotteland and P. Villard, Influence of relative density on granular materials behavior: DEM simulations of triaxial tests, Granular Matter, 2009, 11, 221–236, DOI:10.1007/s10035-009-0138-2.
- B. Saint-Cyr, J. Y. Delenne, C. Voivret, F. Radjai and P. Sornay, Rheology of granular materials composed of nonconvex particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041302, DOI:10.1103/physreve.84.041302.
- F. Ludewig and N. Vandewalle, Strong interlocking of nonconvex particles in random packings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051307, DOI:10.1103/physreve.85.051307.
- C. L. Phillips, J. A. Anderson, G. Huber and S. C. Glotzer, Optimal Filling of Shapes, Phys. Rev. Lett., 2012, 108, 198304, DOI:10.1103/physrevlett.108.198304.
- A. Baulea and H. A. Makse, Fundamental challenges in packing problems: from spherical to non-spherical particles, Soft Matter, 2014, 10, 4423–4429, 10.1039/c3sm52783b.
- H. F. Burcharth, K. d'Angremond, J. W. van der Meer and Z. Liu, Empirical formula for breakage of Dolosse and Tetrapods, Coastal Eng., 2000, 40, 183–206, DOI:10.1016/s0378-3839(00)00010-7.
- S. Remond, J. L. Gallias and A. Mizrahi, Simulation of the packing of granular mixtures of non-convex particles and voids characterization, Granular Matter, 2008, 10, 157–170, DOI:10.1007/s10035-007-0082-y.
- L. N. Zou, X. Cheng, M. L. Rivers, H. M. Jaeger and S. R. Nagel, The packing of granular polymer chains, Science, 2009, 326, 408–410, DOI:10.1126/science.1177114.
- S. A. Galindo-Torres, F. Alonso-Marroquin, Y. C. Wang, D. Pedroso and J. D. M. Castano, Molecular dynamics simulation of complex particles in three dimensions and the study of friction due to nonconvexity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 060301, DOI:10.1103/physreve.79.060301.
- I. Malinouskaya, V. V. Mourzenko, J. F. Thovert and P. M. Adler, Random packings of spiky particles: Geometry and transport properties, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 011304, DOI:10.1103/physreve.80.011304.
- L. M. Lopatina, C. J. O. Reichhardt and C. Reichhardt, Jamming in granular polymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011303, DOI:10.1103/physreve.84.011303.
- J. de Graaf, R. van Roij and M. Dijkstra, Dense Regular Packings of Irregular Nonconvex Particles, Phys. Rev. Lett., 2011, 107, 155501, DOI:10.1103/physrevlett.107.155501.
- E. Brown, A. Nasto, A. G. Athanassiadis and H. M. Jaeger, Strain-stiffening in random packings of entangled granular chains, Phys. Rev. Lett., 2012, 108, 108302, DOI:10.1103/physrevlett.108.108302.
- N. Gravish, S. V. Franklin, D. L. Hu and D. I. Goldman, Entangled Granular Media, Phys. Rev. Lett., 2012, 108, 208001, DOI:10.1103/physrevlett.108.208001.
- L. Y. Meng, S. X. Li, P. Lu, T. Li and W. W. Jin, Bending and elongation effects on the random packing of curved spherocylinders, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061309, DOI:10.1103/physreve.86.061309.
- A. G. Athanassiadis, M. Z. Miskin, P. Kaplan, N. Rodenberg, S. H. Lee, J. Merritt, E. Brown, J. Amend, H. Lipson and H. M. Jaeger, Particle shape effects on the stress response of granular packings, Soft Matter, 2014, 10, 48–59, 10.1039/c3sm52047a.
- S. Gurer, E. Cevik, Y. Yuksel and A. R. Gunbak, Stability of tetrapod breakwaters for different placing methods, J. Coastal Res., 2005, 21, 464–471, DOI:10.2112/00079.1.
- M. Laso, N. C. Karayiannis, K. Foteinopoulou, M. L. Mansfield and M. Kroger, Random packing of model polymers: local structure, topological hindrance and universal scaling, Soft Matter, 2009, 5, 1762–1770, 10.1039/b820264h.
- A. Jain, J. A. Bollinger and T. M. Truskett, Inverse methods for material design, AICHE J., 2014, 60, 2732–2740, DOI:10.1002/aic.14491.
- A. E. Eiben and J. E. Smith, Introduction to evolutionary computing, Springer, New York, 2003 Search PubMed.
- N. Hansen, S. D. Müller and P. Koumoutsakos, Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES), Evol. Comput., 2003, 11, 1–18, DOI:10.1162/106365603321828970.
- A. O. Lyakhov and A. R. Oganov, Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 092103, DOI:10.1103/physrevb.84.092103.
- A. R. Oganov, A. O. Lyakhov and M. Valle, How Evolutionary Crystal Structure Prediction Works-and Why, Acc. Chem. Res., 2011, 44, 227–237, DOI:10.1021/ar1001318.
- E. Bianchi, G. Doppelbauer, L. Filion, M. Dijkstra and G. Kahl, Predicting patchy particle crystals: Variable box shape simulations and evolutionary algorithms, J. Chem. Phys., 2012, 136, 214102, DOI:10.1063/1.4722477.
- L. Filion and M. Dijkstra, Prediction of binary hard-sphere crystal structures, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 046714, DOI:10.1103/physreve.79.046714.
- N. M. O'Boyle, C. M. Campbell and G. R. Hutchison, Computational Design and Selection of Optimal Organic Photovoltaic Materials, J. Phys. Chem. C, 2011, 115, 16200–16210, DOI:10.1021/jp202765c.
- R. Taouche and N. Rouag, Optimization of stress-strain behavior parameters by genetic algorithms method: Application to soft-matrix two-phase alloys, Comput. Mech., 2003, 30, 297–302, DOI:10.1007/s00466-002-0405-0.
- M. T. Tolley and H. Lipson, On-line assembly planning for stochastically reconfigurable systems, Int. J. Robot. Res., 2011, 30, 1566–1584, DOI:10.1177/0278364911398160.
- H. Lipson and J. B. Pollack, Automatic design and manufacture of robotic lifeforms, Nature, 2000, 406, 974–978, DOI:10.1038/35023115.
- J. Qin, G. S. Khaira, Y. Su, G. P. Garner, M. Miskin, H. M. Jaeger and J. J. de Pablo, Optimizing directed self-assembled morphology, Soft Matter, 2013, 9, 11467–11472, 10.1039/c3sm51971f.
- A. F. Hannon, Y. Ding, W. B. Bai, C. A. Ross and A. Alexander-Katz, Optimizing Topographical Templates for Directed Self-Assembly of Block Copolymers via Inverse Design Simulations, Nano Lett., 2014, 14, 318–325, DOI:10.1021/nl404067s.
- G. S. Khaira, J. Qin, G. P. Garner, S. Xiong, L. Wan, R. Ruiz, H. M. Jaeger, P. F. Nealey and J. J. de Pablo, Evolutionary Optimization of Directed Self-Assembly of Triblock Copolymers on Chemically Patterned Substrates, ACS Macro Lett., 2014, 3, 747–752, DOI:10.1021/mz5002349.
- T. I. Zohdi, Genetic design of solids possessing a random-particulate microstructure, Philos. Trans. R. Soc., A, 2003, 361, 1021–1043, DOI:10.1098/rsta.2003.1179.
- R. Zalewski and M. Pyrz, Experimental study and modeling of polymer granular structures submitted to internal underpressure, Mech. Mater., 2013, 57, 75–85, DOI:10.1016/j.mechmat.2012.11.002.
- K. Sobolev and A. Amirjanov, Application of genetic algorithm for modeling of dense packing of concrete aggregates, Construct Build Mater, 2010, 24, 1449–1455, DOI:10.1016/j.conbuildmat.2010.01.010.
- M. Z. Miskin and H. M. Jaeger, Adapting granular materials through artificial evolution, Nat. Mater., 2013, 12, 326–331, DOI:10.1038/nmat3543.
- M. Z. Miskin and H. M. Jaeger, Evolving design rules for the inverse granular packing problem, Soft Matter, 2014, 10, 3708–3715, 10.1039/c4sm00539b.
- J. P. Rolland, B. W. Maynor, L. E. Euliss, A. E. Exner, G. M. Denison and J. M. DeSimone, Direct Fabrication and Harvesting of Monodisperse, Shape-Specific Nanobiomaterials, J. Am. Chem. Soc., 2005, 127, 10096–10100, DOI:10.1021/ja051977c.
- P. F. Damasceno, M. Engel and S. C. Glotzer, Predictive Self-Assembly of Polyhedra into Complex Structures, Science, 2012, 337, 453–457, DOI:10.1126/science.1220869.
| This journal is © The Royal Society of Chemistry 2015 |