 Open Access Article
Open Access ArticleMethods to determine the pressure dependence of the molecular order parameter in (bio)macromolecular fibres†
Arthur Markus
Anton
*a,
Christof
Gutsche
ab,
Wilhelm
Kossack
a and
Friedrich
Kremer
a
aUniversität Leipzig, Fakultät für Physik und Geowissenschaften, Institut für Experimentelle Physik I, Abteilung Molekülphysik, Linnéstraße 5, D-04103 Leipzig, Germany. E-mail: anton@physik.uni-leipzig.de
bUniversität Leipzig, Medizinische Fakultät, Poliklinik für Zahnerhaltung und Parodontologie, Liebigstraße 12, D-04103 Leipzig, Germany
First published on 17th December 2014
Abstract
The experimental realization and an algorithm for analysing the pressure dependence of the molecular order parameter of specific structural moieties in (bio)macromolecular fibres are described. By employing a diamond anvil cell (DAC) the polarization-dependent IR-transmission and in parallel, using an integrated microscope, the macroscopic orientation of the fibres is determined. This enables one to separate between order and disorder at macroscopic and microscopic scales. Using the example of spider silk the pressure dependence of the molecular order parameter of alanine groups being located within nano-crystalline building blocks is deduced and found to decrease reversibly by 0.01 GPa−1 when varying the external hydrostatic pressure between 0 and 3 GPa.
1 Introduction
Orientation on the molecular scale plays a fundamental role in materials science, for example anisotropic mechanical or optical properties.1–3 This information can be obtained by performing orientation-dependent measurements in combination with externally applied mechanical fields as uniaxial stress or hydrostatic pressure.4–6 In case of the latter, high pressure experiments in spectroscopy are performed routinely, wherefore a diamond anvil cell (DAC) is commonly employed.7–10 Due to its geometrical constraints, resulting from two diamonds pressing against a gasket containing the sample within a small hole (<mm), which itself undergoes deformation during pressure application, performing polarization-dependent studies on a macroscopically oriented sample is a challenging task. Materials, that ensure the alignment of the sample, may affect the measurement by their own (background) signals, and furthermore could hamper hydrostaticity due to their mechanical properties. Additionally, access to the sample compartment from outside is impossible after a first application of pressure. Due to that reasons, Colomban et al. used one thick fibre cut properly to fit into the gasket's bore instead of many thin ones to perform polarized Raman spectroscopy.11 Unfortunately, preparing a thicker, and hence less flexible, sample is not possible in any cases. Recently, Ene et al. published X-ray measurements on spider silk, wherefore these highly flexible fibres exhibiting a diameter of 3–5 μm have to be aligned.12 For that, they used a home build pressure cell employing water as pressure transmitting medium being limited to 0.7 GPa.13 However, methods enabling measurements on aligned highly flexible fibres at elevated or high hydrostatic pressures are rare. In the following, we present two novel and easy to use approaches to transfer gratings of aligned fibres into a DAC. Major ampullate spider silk fibres are employed, because its inherent high anisotropy of a β-sheet specific polyalanine vibration5 and the material's great flexibility, emphasize these fibres to an excellent model system probing geometrical misalignment and evaluating a method's feasibility avoiding geometrical distortions. The grating's deformation upon the application of pressure is detected through measuring the apparent dichroic ratio of a specific IR absorption band, as well as, using optical microscopy. With the help of the latter we separate the influence of the macroscopic deformation of the fibre grating from the pressure-dependent microscopic distribution of transition moments, both having an effect on the IR measurement.2 Experimental
Stainless steel gaskets (250 or 300 μm thick) and synthetic type 2a diamonds with a culet size of 1.0 mm are employed. The gasket's pre-indentation is kept at a minimum to overcome any distortion of the grid; just enough to estimate the diamonds' contact area. According to the culet size, a hole with a diameter of 0.5 mm is drilled into the gasket at the middle of the diamonds' contact area. The spider silk samples are made from major ampullate (drageline) silk of the spider Nephila edulis using the method of forced silking.5 The spiders are reared on a diet of crickets.To produce a grating of aligned fibres the following two techniques are used: (A) for one approach a single thread is reeled around two parallel rods.5 Afterwards, one side of the so produced double-sided grating is glued directly on the gasket's surface covering its bore (Method A, Fig. 1a). For that, two-component glue is employed, because this adhesive provides high mechanical resistance while avoiding the effect of solvents. The free standing side of the double-sided grating is removed, enabling to mount the sample into the DAC and eliminating additional absorption and scattering. Please note that the term grating is chosen in analogy to optical grating and does not represent a crossed arrangement. Instead, the fibres are aligned in a parallel fashion since its displacement is controlled by a computer-operated stage.
(B) An other approach to produce a grating of aligned fibres is winding the thread directly around the gasket covering its hole (Method B, Fig. 1b). For that reason, the edges of the initially circular-shaped gasket are flattened. Nail polish is used to fix the fibres on one side of the gasket before cutting off the other side of the grating. This type of glue is employed, because it exhibits excellent wettability. A gap of at least 1 mm is kept between contact site and sample compartment. In addition, alternative approaches requiring enhanced technological efforts compared to the two afore-mentioned ones are provided in the ESI.†
After the hole within the gasket is covered with a grating of aligned spider silk fibres, paraffin oil is added which reduces light scattering of the fibres without affecting their mechanical properties5 and also acts as pressure transmitting medium.6,14 Hydrostatic pressure is applied by means of a μScopeDAC-HT(G) diamond anvil cell (easyLab) and determined in situ from the pressure-dependent shift of the ruby R1 fluorescence line.15 Infrared spectra are recorded in transmission mode on a Fourier-transform-infrared (FTIR)-spectrometer (FTS 6000, BioRad) equipped with an IR-microscope (UMA-500, BioRad) and a mercury–cadmium–telluride (MCT) detector (Kolmar Technologies) using a spectral resolution of 4 cm−1. The IR-light is linearly polarized before entering the DAC (for details regarding the setup see the ref. 5 and 6).
The difference of the vibrational absorption at ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = 965 cm−1 depending on the IR light's polarization, typical for major ampullate spider silk, is utilized to determine the dichroic ration (cf.eqn (2) and molecular order parameter ESI S2) of the β-sheet polyalanine nanocrystals embedded in an glycine-rich amorphous, glassy matrix.5,16 As long as one employs a grating of parallel fibres the dichroic ratio of this arrangement is identical to that of a single fibre and one is able to extract information of the microscopic orientation of the IR transition moments.1,5 In case the spider silk grating is deformed and the fibres' alignment is distorted, the outcome of the IR measurement depends on the microscopic orientation of the IR transition moments, as before, but also on the macroscopic geometrical orientation of the fibres. To evaluate the latter and to separate its influence on the IR measurements from the pressure-dependent microscopic orientation, we make use of optical microscopy as independent technique complimentary to IR spectroscopy.
= 965 cm−1 depending on the IR light's polarization, typical for major ampullate spider silk, is utilized to determine the dichroic ration (cf.eqn (2) and molecular order parameter ESI S2) of the β-sheet polyalanine nanocrystals embedded in an glycine-rich amorphous, glassy matrix.5,16 As long as one employs a grating of parallel fibres the dichroic ratio of this arrangement is identical to that of a single fibre and one is able to extract information of the microscopic orientation of the IR transition moments.1,5 In case the spider silk grating is deformed and the fibres' alignment is distorted, the outcome of the IR measurement depends on the microscopic orientation of the IR transition moments, as before, but also on the macroscopic geometrical orientation of the fibres. To evaluate the latter and to separate its influence on the IR measurements from the pressure-dependent microscopic orientation, we make use of optical microscopy as independent technique complimentary to IR spectroscopy.
3 Results and discussion
After producing a grating of aligned fibres and transferring it into the DAC, the sample and the gasket are deformed as the pressure is applied for the first time resulting in a loss of the fibres' alignment (Fig. 2). Despite a clearly visible deterioration, certain areas with fibres in parallel can still be found. On expense of signal-to-noise ratio and measurement time, the region of interest (ROI) of the focusing optics can be reduced resulting in a more-pronounced spectral dichroism and finally a larger order parameter. This argument is valid for both Method A and B described above. | ||
| Fig. 2 A scheme illustrating how to determine the macroscopic, geometrical orientation of the spider silk fibres (here after subsequent pressure cycles). A micrograph is divided up into equally sized squares (50 × 50 pixel) in which the orientation angle with respect to vertical orientation is estimated. The bright square indicates the 250 × 250 μm2 ROI of the IR microscope. A histogram is compiled corrected for locating the mean at 0°, as automatically performed when applying eqn (1) on the measured spectra. The solid line indicates an optional fit assuming a sum of two Gaussian distribution functions. The obtained parameters can be found in Table 1. | ||
Especially when using Method B, it is noteworthy that due to the insufficient pre-indentation, the gasket's bore expands with rising pressure,10,17 causing an elliptical shape of the hole. This deformation is a result of the gasket's asymmetric shape and affects the previously cut edges, because of a lack of material at these sites. At (2.0 or 2.7 ± 0.2) GPa (derived from the externally applied membrane pressure) the hole enlarges as wide as the pressure is not preserved anymore. Large expansion of the bore can lead to damage on the diamonds,10 however, in both of our experiments performed using Method B, the diamonds remained intact.
For estimating the geometrical distribution of the fibres, a micrograph of the sample compartment is divided into equal square regions, where the fibres are in parallel and their orientation angle relative to a fixed direction can be estimated (Fig. 2). Afterwards, a histogram of orientation angles modelling the fibres arrangement within the image plane is compiled. The heights of the histogram bars are corrected to overcome any deviation of the fibre length, and consequently the sample volume, within a square region depending on the orientation angle (h = h0/cos(θ)). Additionally, it is possible to fit a Gaussian function (or a sum of those) to the histogram enabling a continuous description of the fibres' distribution.
To specify the alignment of the sample fibres in a more refined way, polarization-dependent FTIR spectra are recorded and corrected for the (also pressure-dependent) paraffin absorption. For that a polarization-independent peak at 890 cm−1 is used as a measure for the sample's paraffin content. Especially in case of this sample arrangement, the volume of the pressure transmitting medium is significantly higher than for other measurements (≈100× compared to former experiments5,6), resulting in an enhanced background signal. As a consequence of refractive index mismatch and birefringent properties of spider silk, clear interference patterns are evident in the paraffin background spectra which has to be reassessed, while those are absent in case of the spider silk measurements. After subtraction of a linear baseline from the paraffin-corrected spectra, the well separated polyalanine peak is modelled with a pseudo-Voigt function, as proposed by Stancik and Brauns.18 Afterwards, the maximum absorbance Amax appearing at a polarization angle Ω is determined through fitting eqn (1) to the data:
A(ϕ) = −log10[10−Amax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(ϕ − Ω) + 10−Amin cos2(ϕ − Ω) + 10−Amin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(ϕ − Ω)], sin2(ϕ − Ω)], | (1) |
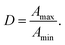 | (2) |
Note that we are focusing on the dichroic ratio as physical quantity instead of the order parameter, because to calculate the latter all three values of the absorbance strength relative to the principle axes has to be known, but only two of them can be measured directly when the sample is inside the DAC. Consequently, assumptions has to be made to work out the molecular order parameter based on the measured dichroic ratio, which are well justified in case of rotational symmetric fibres (see ESI S1†).
In case the spider silk fibres are aligned and form a grating (reeled around two parallel rods) a dichroic ratio of DrefA = 22.4 ± 0.5 or DrefB = 20.1 ± 0.5 (SrefA = 0.88 ± 0.01, SrefB = 0.86 ± 0.01) can be found (Fig. 3a). In case the sample is prepared using Method A, a deteriorated dichroism becomes evident (Fig. 3b) and the dichroic ratio decreases to DA = 5.5 ± 1.1 when closing the pressure cell, due to the sample grating's misalignment. A measurement uncertainty for fitting the integrated absorbance of 5% is estimated, resulting in a total uncertainty of 20% for the dichroic ratio of samples under load. The reference samples are not concerned here. During the application of hydrostatic pressure DA is reduced further, but the initial value is restored during relaxation without any indication of hysteresis or persistent deterioration (Fig. 3g). Performing a second measurement cycle might detect additional plastic deformations, which are absent in our study.
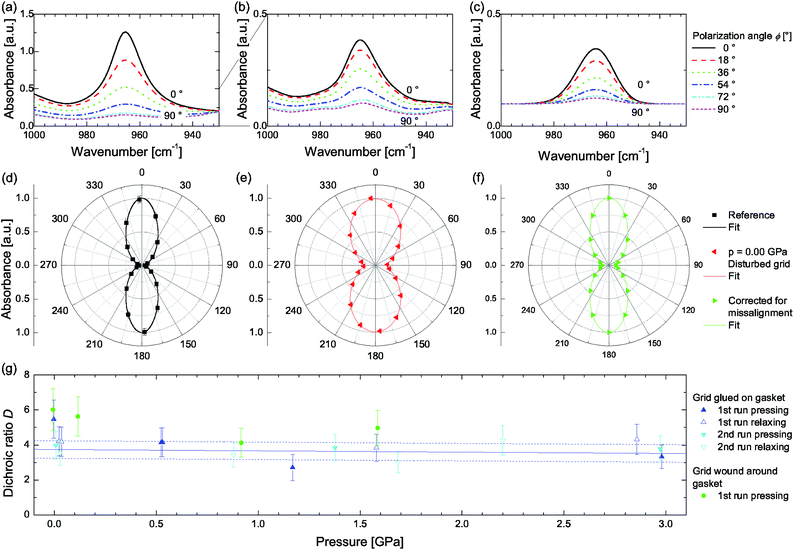 | ||
| Fig. 3 Polarization-dependent spectra showing IR-dichroism of the band located at 965 cm−1 representing the alanine moiety (a) for a fresh, native reference sample (wound around rods), (b) after closing the DAC at 0.00 GPa, and (c) recalculated by correcting for the geometrical distortion of the grating. (d–f) Polar representation of (a)–(c) normalized to 1 along with fits according to eqn (1). (g) Apparent dichroic ratio D depending on the applied hydrostatic pressure. The blue line represents a linear fit, while the dashed lines correspond to D ± 0.5. | ||
In case of Method B the dichroic ratio appears to be slightly reduced when the thread is wound directly around the gasket (DrefB = 17.3 ± 0.5, SrefB = 0.84 ± 0.02) compared to winding around rods (see above). This reduction is caused by exchanging rods exhibiting a circular cross section, where the thread can cling to their smooth surface, by a flattened, 300 μm thick gasket with sharp edges. Despite the fact that the hole of the gasket has a diameter of 500 μm, whereas the microscope's ROI amounts to 250 × 250 μm2, it is not possible to excluded it as additional optical element deteriorating the measurement conditions. However, similar to Method A, DB is reduced upon closing the cell due to geometrical distortions of the grating to DB = 6.0 ± 1.2, exhibiting a slightly larger value compared to DA. A possible explanation might be found in the sample preparation. In Method A the grating is glued on the gasket's surface resulting in a gap due to the adhesive, whereas in Method B the thread is in direct contact to the gasket's surface. This gab may cause a stronger misalignment, and hence, a lowered dichroism.
To estimate the reversible change of the dichroic ratio in the range from 0 to 2.98 GPa a linear function is fitted to the measured values of D which results in a slope of aA = (−0.07 ± 0.14) GPa−1 and an intercept of bA = 3.74 ± 0.23. In that way one is able to separate the decrease of the apparent dichroic ratio, due to geometrical misalignment from closing the DAC, and its variation as a result of hydrostatic pressure.
To model the molecular order parameter of a rotationally symmetric fibre (or a grating of the fibres in parallel) we introduce the second Legendre polynomial as a definition of the molecular order parameter19
 | (3) |
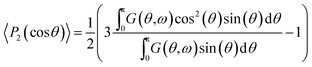 | (4) |
Note that averaging (〈…〉) over all illuminated molecules is inherent in IR absorption measurements. Assuming a Gaussian shaped dipole distribution density G(θ) with its central moment θ0 located at 0° (as derived from polarization measurements on fibres in parallel5) and a certain distribution width ω0,
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, ω)〉 and D (ESI S2†) one is able to obtain the width of the microscopic dipole distribution as ω0 = 12.0°, 12.7°, and 13.6°.1 Note that the second term (θ(2)0 = θ(1)0 + 180°) results from periodic boundary conditions and has nothing to do with mathematical derivative. Normalization to 1 is maintained when integrating G(θ) from θ = 0° to 180°.
θ, ω)〉 and D (ESI S2†) one is able to obtain the width of the microscopic dipole distribution as ω0 = 12.0°, 12.7°, and 13.6°.1 Note that the second term (θ(2)0 = θ(1)0 + 180°) results from periodic boundary conditions and has nothing to do with mathematical derivative. Normalization to 1 is maintained when integrating G(θ) from θ = 0° to 180°.
Furthermore, to model the system composed of rotationally symmetric fibres forming a disturbed grating it is useful to describe it through the microscopic distribution of the molecular transition dipole moments within one fibre G(θ) convolved with the geometrical (macroscopic) distribution of the fibres Ḡ(ϑ, ϕ). The microscopic dipole distribution is handled as stated in the former paragraph. The geometrical distribution of the fibres is deduced from a micrograph of the fibres' arrangement within the sample compartment as describe above. Additionally, we assume that the grating's deformation, and hence geometrical distortion, mainly take place within a plane parallel to the diamonds' surfaces (xz plane). This is justified, because the grating is in direct contact to one diamond at which it is supported. Due to the deformation, rotational symmetry, as in case of fibres in parallel orientation along the z direction, is not adequate anymore. To handle the asymmetry, Ḡ(ϑ, ϕ) is separated into two terms: one describes the fibres' orientation within the xz plane and is assigned to cos2(ϕ) (x direction), the other is assigned to sin2(ϕ) and describes the geometry in the yz plane (y direction). In case there would be no difference between the dipole distributions in the two directions (Ḡx = Ḡy) one is able to apply sin2(ϕ) + cos2(ϕ) = 1 with the result that Ḡ(θ, ϕ) is independent of ϕ and the system exhibits rotational symmetry. Because the dipole distribution within the yz plane is much less affected by geometrical distortions than within the xz plane, the former can be treated analogously to the undisturbed case, wherefore Ḡy is modelled by a Dirac delta function δ(ϑ) resulting in 1 during the convolution process. Thus, we define
| Ḡ(ϑ, ϕ) = Ḡx(ϑ)cos2(ϕ) + Ḡy(ϑ)sin2(ϕ) | (6) |
 | (7) |
| Ḡy(ϑ) = δ(ϑ − 0). | (8) |
Ñ(ϑi) represents the counts of the histogram N(ϑi) according to the fibre segment's direction ϑi ∈[−30°, −25°, …, +30°] corrected for the angle-dependent sample volume within one square region Ñ(ϑi) = N(ϑi)/cos(ϑi).
After equating the principle axes of the microscopic (fibre fixed) and macroscopic (geometrical) coordinate systems (θ = ϑ) and performing the convolution (ESI S3†) one obtains the dipole distribution density of the geometrical disturbed grating ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (θ, ϕ) which allows for the determination the absorbance strength with respect to the principle axes (Axx, Ayy, and Azz) and, hence, the dichroic ratio, as well as, order parameter values.1
(θ, ϕ) which allows for the determination the absorbance strength with respect to the principle axes (Axx, Ayy, and Azz) and, hence, the dichroic ratio, as well as, order parameter values.1
 | (9) |
 | (10) |
 | (11) |
The parameter C represents measurement-dependent values (C = E02μ02N) as the electric field strength or the transition dipole moment, as well as a normalization constant ( ). When calculating the dichroic ratio within the xz plane,
). When calculating the dichroic ratio within the xz plane,
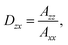 | (12) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (θ, ϕ) deduced from the microscopic description G(θ|θ0 = 0°, ω0 = 13.6°) convolved with the fibre orientation Ḡ(ϑ, ϕ) as derived form the micrograph and the histogram, the apparent dichroic ratio can be obtained as Dzx = 7.2. It is evident, that this value is higher than the ratio found in case of the spectral measurements indicating a less oriented sample as presumed. Alternatively, using the fitted Gaussian function results in Dzx = 4.5 underestimating the fibres alignment, as already evident in the not-matching wings of the distribution function (Fig. 2 and ESI S4†).
(θ, ϕ) deduced from the microscopic description G(θ|θ0 = 0°, ω0 = 13.6°) convolved with the fibre orientation Ḡ(ϑ, ϕ) as derived form the micrograph and the histogram, the apparent dichroic ratio can be obtained as Dzx = 7.2. It is evident, that this value is higher than the ratio found in case of the spectral measurements indicating a less oriented sample as presumed. Alternatively, using the fitted Gaussian function results in Dzx = 4.5 underestimating the fibres alignment, as already evident in the not-matching wings of the distribution function (Fig. 2 and ESI S4†).
So far, we have demonstrated that the spectral dichroism as derived from IR measurements can be treated as convolution of the microscopic transition dipole distribution within a single fibre and the macroscopic, geometrical distribution of the fibres inside the DAC in fair agreement (20% accuracy) to the measured values. The outcome of the IR experiment depends on both, the microscopic and the macroscopic distribution, whereas optical microscopy can only be used to determine the macroscopic one. By comparing the IR and microscopy measurements, information of the microscopic distribution can be obtained. Hereafter we discuss possible factors that can influence the deviation of D and Dzx and derive the change of the microscopic transition moment distribution in dependence on hydrostatic pressure.
Associated with recalculating the dichroic ratio we try to correct the measured dichroism. For that purpose, we fix the geometrical distribution Ḡ(ϑ, ϕ) while comparing the dichroic ratio depending on a variable microscopic distribution width ω0 with the measured values. Despite the integration during calculating the absorbance values (eqn (9)–(11)) is limiting the determination of an analytical inverse function, the dichroic ratio depending on the expectation θ0 and the width ω0 of the underlying microscopic distribution shows a strict monotonic dependence. Thus, it is handled as an injective transformation and an inverse function exists on a confined region, even when not expressible analytically.21 Hence, parameterization of this dependence allows for backward determination. Taking ω0 = 18.1° a value of D = 5.5 similar to the on deduced from the spectral measurements is achieved (Fig. 3f). In the former it is shown, that closing the DAC while misaligning the grating at ambient pressure reduces the dichroic ration to a greater extend than the application of hydrostatic pressure afterwards. Thus, an increase of the microscopic distribution width of 33% of the value of the undisturbed cases is not reasonable. That is why, we believe the origin of the deviation between the calculated and the measured values lies solely in geometry.
Basing on the reasons that are reduce the dichroic ratio we investigate the influence of the fibre orientation. For that purpose, we introduce a model function representing the fibres' (mis-)alignment within the xz plane by replacing Ḡx (eqn (7)) with
 | (13) |
Assuming a geometrical distribution as described by eqn (6), (8) and (13) and using ω0 = 13.6° and ω1 = 18.9° one obtains a dichroic ratio of D = 5.5, in accordance with our measurements, and an apparent order parameter of S = 0.68 (eqn S1†). For comparison, the application of eqn S2† would result in S = 0.60 clearly underestimating the ordering of the sample, because the separation between x and y direction is not done.
Taking the parameters aA and bA as derived from fitting a linear dependence on the apparent dichroic ratio under hydrostatic pressure (Fig. 3g) we are able to correlate the varying dichroic ratio during pressure application with an altered microscopic dipole distribution width. Note that for estimating the parameters of Table 2 we assume a preserved geometry during pressing and relaxing runs, as indicated by micrographs, and a linear dependence between D and S which, in fact, is not the case over the hole range of possible values, but applicable for the limited range of this experiment.
| ϑ 1 | −22.7° | ω 1 | 14.4° | B 1 | 8434 |
| ϑ 2 | 15.7° | ω 2 | 7.7° | B 2 | 4070 |
| D | ω 0 | ω 1 | S |
|---|---|---|---|
| 3.74 | 13.6° | 24.7° | 0.59 |
| 3.52 | 16.0° | 24.7° | 0.56 |
| Δω0 = 0.8° GPa−1 | ΔS = 0.01 GPa−1 | ||
The clear distinction between the microscopic, rotationally symmetric transition dipole moment distribution density of a single (spider silk) fibre and the asymmetric geometric distribution of the fibres within the DAC allows for correcting the apparent (molecular) order parameter. Assuming a negligible misalignment of the grating within the yz plane (perpendicular to the diamonds' surfaces) compared to the deformation within the xz plane we are able to calculate the value of the molecular order parameter without oversimplifying assumptions, for instance macroscopic rotational symmetry. Although the preserved orientation of the fibres in y direction (along the optical axis) in the current study is well justified, it is still an assumption. Remedy could be provided, for example, by staining the fibres fluorescently and following their trace employing a laser scanning confocal microscope.
4 Conclusion
A method and its experimental realization to carry out pressure dependent measurements on the molecular order parameter of highly anisotropic samples, as fibres of spider silk for instance, is described. When applying hydrostatic pressure the sample in the Diamond Anvil Cell (DAC) becomes unavoidably misaligned. However, through employing image analysis and an appropriate mathematical formalism, the macroscopic disorder of the sample is quantitatively determined. After correcting for the background signal of the pressure transmitting medium (in this study paraffin oil), the pressure dependence of the IR dichroism of a specific absorption band (polyalanine vibration at 965 cm−1) is deduced.In summary, order and disorder at macroscopic and microscopic scales are separated enabling to determine the pressure dependence of the molecular order parameter of the alanine moieties being located within the nano-crystalline building blocks of spider silk. The response of the molecular order parameter to hydrostatic pressure up to a value of 3 GPa is obtained as 0.01 GPa−1.
Acknowledgements
The authors would like to thank Wycliffe Kipnusu, Emanuel Mapesa, and Thomas Michael for their helpful advices on language and mathematics. Financial support by the Deutsche Forschungsgemeinschaft (DFG) Project B5 within SFB/TRR 102 “Polymers under multiple constraints: restricted and controlled molecular order and mobility” and through the Leipzig School of Natural Sciences “Building with Molecules and Nano-Objects” (BuildMoNa) is highly acknowledged.References
- Vibrational Spectroscopy of Polymers: Principles and Practice, ed. P. R. G. Neil, J. Everall and J. M. Chalmers, John Wiley & Sons Ltd., 2007 Search PubMed.
- M. V. Kakade, S. Givens, K. Gardner, K. H. Lee, D. B. Chase and J. F. Rabolt, J. Am. Chem. Soc., 2007, 129, 2777–2782 CrossRef CAS PubMed.
- V. Fasano, M. Baroncini, M. Moffa, D. Iandolo, A. Camposeo, A. Credi and D. Pisignano, J. Am. Chem. Soc., 2014, 136, 14245–14254 CrossRef CAS PubMed.
- Polymer Spectroscopy, ed. A. H. Fawcett, John Wiley & Sons Ltd., 1996 Search PubMed.
- P. Papadopoulos, J. Sölter and F. Kremer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 193–199 CrossRef CAS PubMed.
- A. M. Anton, W. Kossack, C. Gutsche, R. Figuli (Ene), P. Papadopoulos, J. Ebad-Allah, C. Kuntscher and F. Kremer, Macromolecules, 2013, 46, 4919–4923 CrossRef CAS.
- A. Jayaraman, Rev. Mod. Phys., 1983, 55, 65–108 CrossRef CAS.
- A. Jayaraman, Rev. Sci. Instrum., 1986, 57, 1013–1031 CrossRef CAS PubMed.
- D. J. Dunstan and I. L. Spain, J. Phys. E: Sci. Instrum., 1989, 22, 913 CrossRef CAS.
- I. L. Spain and D. J. Dunstan, J. Phys. E: Sci. Instrum., 1989, 22, 923 CrossRef CAS.
- P. Colomban, G. Sagon, M. Lesage and J. M. H. Ramirez, Vib. Spectrosc., 2005, 37, 83–90 CrossRef CAS PubMed.
- R. Ene, C. Krywka, S.-G. Kang, P. Papadopoulos, M. Burghammer, E. D. Cola, M. Müller and F. Kremer, Polymer, 2012, 53, 5507–5512 CrossRef CAS PubMed.
- C. Krywka, C. Sternemann, M. Paulus, M. Tolan, C. Royer and R. Winter, ChemPhysChem, 2008, 9, 2809–2815 CrossRef CAS PubMed.
- J. W. Otto, J. K. Vassiliou and G. Frommeyer, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3253–3263 CrossRef CAS.
- K. Syassen, High Pressure Res., 2008, 28, 75–126 CrossRef CAS.
- R. Ene, P. Papadopoulos and F. Kremer, Soft Matter, 2009, 5, 4568–4574 RSC.
- D. J. Dunstan, Rev. Sci. Instrum., 1989, 60, 3789–3795 CrossRef PubMed.
- A. L. Stancik and E. B. Brauns, Vib. Spectrosc., 2008, 47, 66–69 CrossRef CAS PubMed.
- M. Warner and E. M. Terentjev, Liquid Crystal Elastomers, Oxford University Press, 2003 Search PubMed.
- J. Michl and E. W. Thulstrup, Spectroscopy with polarized light, VHC Publishers, Inc., 1995 Search PubMed.
- Taschenbuch der Mathematik, ed. I. N. Bronstein, K. A. Semendjajew, G. Musiol and H. Mühlig, Verlag Harri Deutsch, Thun and Frankfurt (Main), 2001 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The definition of the molecular order parameter in general and in case of rotation symmetry (S1), the conversion between the molecular order parameter and the dichroic ratio (S2), the convolution of a Gaussian distribution function with a discrete distribution function (S3), and the convolution of two Gaussian functions (S4), as well as, eqn S1 and S2. See DOI: 10.1039/c4sm01142b |
| This journal is © The Royal Society of Chemistry 2015 |

