The boron–boron triple bond in NHC→B≡B←NHC

Abstract

Quantum chemical calculations of the compound B₂(NHC^Me)₂ and a thorough examination of the electronic structure with an energy decomposition analysis provide strong evidence for the appearance of boron–boron triple bond character. This holds for the model compound and for the isolated diboryne B₂(NHC^R)₂ of Braunschweig which has an even slightly shorter B–B bond. The bonding situation in the molecule is best described in terms of NHC^Me→B₂←NHC^Me donor–acceptor interactions and concomitant π-backdonation NHC^Me←B₂→NHC^Me which weakens the B–B bond, but the essential features of a triple bond are preserved. An appropriate formula which depicts both interactions is the sketch NHC^Me⇄B≡B⇄NHC^Me. Calculations of the stretching force constants F_BB which take molecules that have genuine single, double and triple bonds as references suggest that the effective bond order of B₂(NHC^Me)₂ has the value of 2.34. The suggestion by Köppe and Schnöckel that the strength of the boron–boron bond in B₂(NHC^H)₂ is only between a single and a double bond is repudiated. It misleadingly takes the force constant F_BB of OBBO as the reference value for a B–B single bond which ignores π bonding contributions. The alleged similarity between the B–O bonds in OBBO and the B–C bonds in B₂(NHC^Me)₂ is a mistaken application of the principle of isolable relationship.

---

Introduction

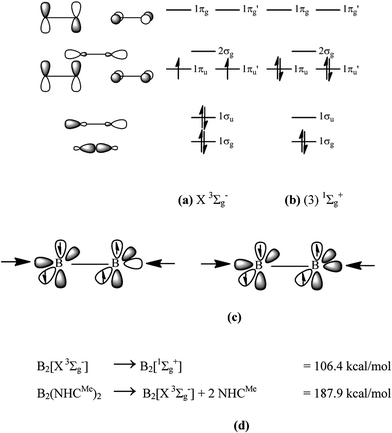
In 2012, Braunschweig and co-workers reported the synthesis of the diboryne compound B₂(NHC^R)₂ where diatomic B₂ binds two N-heterocyclic carbenes (NHC) which carry bulky groups R at nitrogen.¹ The X-ray structure analysis revealed a linear arrangement of the NHC^R ligands to the central B₂ moiety and a very short B–B bond of 1.45 Å which agrees with the standard value for a triple bond (1.46 Å).² An earlier theoretical study that was published in 2011 had predicted that the molecule has very strong bonds which can be interpreted in terms of donor–acceptor interactions NHC^R→B₂←NHC^R where diatomic B₂ is in the highly excited (3) ¹Σ_g⁺ singlet state rather than in the X ³Σ_g⁻ ground state (Fig. 1a and b).³

Fig. 1 Schematic diagram of the valence orbitals and orbital occupation of B₂ in (a) X ³Σ_g⁻ ground state and (b) (3) ¹Σ_g⁺ excited state. (c) Schematic representation of the charge donation from the out-of-phase (+,−) and in-phase (+,+) combinations of the ligand lone-pair σ orbitals into the vacant orbitals of B₂ in the ¹Σ_g⁺ excited state. (d) Calculated energies of the excitation energy of B₂ from the ground state to the reference state and bond dissociation energy D_e of B₂(NHC^Me)₂ at BP86/def2-TZVPP.

Charge donation from the ligands takes place into the empty 1σ_u MO (out-of-phase +,− donation) and the 2σ_g MO (in-phase +,+ donation) which is schematically shown in Fig. 1c. In addition to the σ-donation NHC^R→B₂←NHC^R, π-backdonation NHC^R←B₂→NHC^R may occur from the occupied 1π_u and 1π_u′ orbitals which would weaken the B≡B triple bond. An energy decomposition analysis was carried out in 2013 which suggests that 2/3 of the total orbital interactions comes from NHC^R→B₂←NHC^R σ-donation and 1/3 comes from NHC^R←B₂→NHC^R π-backdonation.⁴ Thus, the bond order for the B–B can be expected between 2 and 3 while the triple bond character is retained in the diboryne whose bonding situation is properly sketched with the formula NHC^R⇄B≡B⇄NHC^R.

Very recently, Köppe and Schnöckel (KS) published in this journal a reinterpretation of the boron–boron bond in NHC^R→B₂←NHC^R where they question the assignment of a triple bond.⁵ Using thermodynamic arguments and a correlation of force constants, KS suggest that the strength of the boron–boron bond in NHC→B₂←NHC is only between a single and a double bond and that the molecule should better become described with traditional resonance structures. The conclusion of KS was made on the basis of selected experimental and calculated results. The authors write that their results ‘…generates a new interpretation which is in contrast to the triple bond donor–acceptor description visualized by arrows and which casts a critical light on the interpretation of any NHC “stabilized” molecule’. The statement was made without reference to the previous quantum chemical studies of B₂(NHC^R)₂^3,4,6 nor to any other theoretical work about NHC stabilized molecules.⁷

We studied the paper by KS⁵ very carefully and noticed several flaws in their arguments which cast severe doubts on their conclusions. In the following we critically discuss the approach and the conclusions of the authors. Our counter arguments are presented in the same order as in the paper by KS.

Thermodynamic view

KS begin their discussion with a lengthy description of the energy which is required for the formation of B₂ in the excited (3) ¹Σ_g⁺ state (which is denoted as B₂* in their paper) from solid boron in a gas-phase reaction which is irrelevant for the discussion of the bonding situation and for the formation and stability of the compound. The compound NHC^R→B₂←NHC^R was prepared by Braunschweig by reacting NHC^R→(B₂Br₄)←NHC^R with sodium naphthalenide in THF solution which gives the product molecule via debromination reaction.¹ It is well known that molecules which have a large positive heat of formation can be isolated as stable compounds in straightforward reactions if the electronic structure is favourable.⁸ KS arrive at the conclusion: “Therefore, nobody would conclude that B₂* is stabilized in solid boron!”. But nobody ever claimed that solid boron would do that! What has been claimed is the significant stabilization of B₂* through strong donor–acceptor interactions with NHC ligands.^3,4,6

KS make the statement that the arrows in the formula NHC→B₂←NHC “suggest only a weak donor (NHC)–acceptor (B₂*) interaction in which the bonding of the educt is still visible”. But it was already shown in 2013³ that the donor–acceptor interactions NHC→B₂←NHC are very strong, which should be expected in light of the low-lying vacant orbitals of B₂* (Fig. 1). The strong interactions do not lead to major changes in the structures of the donor and acceptor species which is easy to understand. The two vacant σ orbitals in B₂* are bonding and antibonding, respectively, which roughly cancel the impact of the donor–acceptor interactions on the B–B bond length. The slightly longer B–B distance in NHC^R→B₂←NHC^R (1.45 Å) than in free B₂* (1.40 Å) is caused by π-backdonation from B₂ to the NHC ligands. The geometry changes of the NHC ligands in NHC^R→B₂←NHC^R are likewise rather small, because they involve mainly the carbene lone-pair orbital. Thus, the structure and stability of NHC→B₂←NHC are in full accord with the bonding situation of a B≡B moiety which is stabilized by strong σ-donation of and π-backdonation to the NHC ligands.

Determination and discussion of the force constants in NHC→B₂←NHC

The main argument in the paper by KS against a triple bond character in NHC^R→B₂←NHC^R rests on the force constants of the B–B stretching mode. The authors first discuss several molecules which may be used as reference for a B–B single bond. They choose OBBO as candidate, because it would “have a BB bonding situation similar to 1 with a linear X–B–B–X moiety” where 1 stands for NHC^R→B₂←NHC^R. In order to underpin the connection between OBBO and 1 the authors refer to the isolobal relationship OCH₂. Then they write that “the Lewis formula O=B–B=O is in accordance with the values of the BB and BC force constants”.

There are two major flaws in the above arguments. One flaw concerns the suggestion that the boron–boron bond in OBBO is a single bond.⁹ There are two orthogonal π components in the BO moieties which conjugate over the BB fragment. Using OBBO as template for a B–B single bond ignores the contribution of B–B π-bonding. Note that the authors suggest a Lewis structure O=B–B=O for the molecule which has an electron sextet at boron. The second flaw is the suggestion that the isolobal relationship OCH₂ may be used to indicate a similar bonding situation in OBBO and NHC^R→BB←NHC^R. CH₂ has an electronic (³B₁) triplet ground state which is 9.0 kcal mol⁻¹ below the (¹A₁) singlet state.¹⁰ Methylene is isolobal with oxygen atom, because both species have a triplet state and a similar shape and energy.¹¹ In contrast, NHC has a singlet ground state which is 85 kcal mol⁻¹ below the triplet state.¹² It means that the electronic structure and the chemical reactivity of the carbene carbon atom of NHC are very different from CH₂, which is common knowledge in chemistry.¹³ A pertinent example which demonstrates the large difference between the two carbenes is given by the compounds where they bind to a single carbon atom. C(CH₂)₂ is the parent allene H₂C=C=CH₂ which has a linear structure with C=C double bonds and perpendicular CH₂ planes. C(NHC)₂ is a carbone CL₂ which features two donor–acceptor bonds L→C←L to a carbon atom which retains two electron lone pairs.¹⁴ The carbodicarbene C(NHC^Me)₂ has a bond angle (NHC^Me)–C–(NHC^Me) of 132° ¹⁵ which is similar to the isolobal carbodiphosphorane C(PPh₃)₂ which has a bond angle of 135°.¹⁶ The first carbodicarbenes C(NHC^R)₂ were recently synthesized by Bertrand and by Fürstner.¹⁷ It is obvious that the isolobal relationship OCH₂ does not hold for NHC.

We searched for a molecule which possesses a genuine B–B single bond. The vast experimental information which has been accumulated about boron compounds clearly shows that boron atoms in stable molecules have at least partially filled four valence AOs which makes the search for an experimental value of species with a B–B single bond futile. We therefore looked for a model compound with a genuine B–B single bond that can be calculated with an accuracy that rivals experimental values. A suitable species is planar H₂B–BH₂ where the p(π) orbitals of boron are vacant. The planar (D_2h) structure is a transition state for the rotation about the B–B bond of B₂H₄ which has a perpendicular (D_2d) equilibrium structure. The B–B bond in the D_2d energy minimum structure has been calculated to be much shorter (1.623 Å) than in the planar form (1.752 Å) which is due to significant hyperconjugation that was estimated from the energy difference between the D_2d and D_2h structures (17.3 kcal mol⁻¹).¹⁸ The reported B–B bond length of 1.65 Å for OBBO which is much shorter than the single bond in planar B₂H₄ (1.752 Å) indicates a substantial degree of B–B π-bonding which makes the molecule unsuitable as reference for a single bond.

We calculated the force constant for the B–B stretching mode in planar H₂B–BH₂ and took the value of F_BB = 2.49 mdyn Å⁻¹ as reference value for a B–B single bond. A related molecule with a genuine B=B double bond is HBBH in the (³Σ_g⁻) triplet state which has a B–B σ bond and two singly occupied B–B π orbitals. The calculated force constant for the B–B stretching mode is F_BB = 5.38 mdyn Å⁻¹ which is taken as reference value for a B=B double bond. The reference value for a B≡B triple bond comes from the calculated force constant for the (3) ¹Σ_g⁺ state of B₂ which has the value of F_BB = 7.62 mdyn Å⁻¹. The B–B force constants in mdyn Å⁻¹ of the hydroboranes for a single bond (2.49; planar B₂H₄), double bond (5.38, triplet B₂H₂) and triple bond (7.62; (3) ¹Σ_g⁺ B₂) exhibit the same ratio 1 : 2 : 3 as the force constants F_CC for the C–C bonds in the analogous hydrocarbons which were given by KS as 4.4 (C₂H₆), 9.1 (C₂H₄) and 15.6 (C₂H₂).⁵ The regular increase of the force constant is at first sight a bit surprising, since the additional components of the multiple bonds are π bonds which are weaker than σ bonds. Along with the addition of π bonding, there is a concomitant change in the hybridisation of the σ bond which enhances the overall bonding and leads to the approximate relation 1 : 2 : 3.¹⁹

Fig. 2 shows a correlation diagram between the force constants and the bond orders of the reference compounds H₂B–BH₂ (planar), HB=BH (³Σ_g⁻) and B₂ ((3) ¹Σ_g⁺) which exhibits a linear correlation coefficient of R² = 0.995. The calculated force constant F_BB = 3.5 for OBBO suggests a bond order of 1.36, which indicates a significant contribution of π bonding. The force constant F_BB = 6.0 which was calculated by KS for NHC→B₂←NHC now indicates an effective bond order for the B–B bond of 2.34. This is in agreement with the classification as a molecule which has a B≡B triple bond that is weakened by π-backdonation. The assignment of the much lower bond order of 1.5 for the complex which was suggested by KS is misleading, because it arbitrarily uses a bond order of 1.0 for OBBO, which neglects the π contribution to the B–B bond.

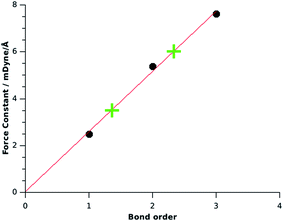Fig. 2 Correlation between the force constants F_BB for boron–boron single, double and triple bonds (•) and the values for OBBO and B₂(NHC^Me)₂ (+).

Bonding analysis of NHC→B₂←NHC

The above discussion provides information about the relative strength of the B–B bond in the complex NHC^R→B₂←NHC^R compared with reference compounds which were chosen by KS (OBBO) and by us (planar H₂BBH₂, triplet HBBH and (3) ¹Σ_g⁺ B₂) which, however, does not give insight into the nature of the bonding. Quantitative information is available form EDA-NOCV²⁰ (Energy Decomposition Analysis²¹ combined with Natural Orbitals for Chemical Valence²²) calculations. The advantage of the recently developed EDA-NOCV method over the EDA procedure which we used in our earlier bonding analysis⁴ of NHC^Me→B₂←NHC^Me is, that the orbital interactions are broken down to a sum of pairwise contributions which provides detailed information about the strength of specific pairs of orbitals. The results give a complete picture of the bonding between the interacting fragments which can be connected with classical bonding models of chemistry. A helpful feature of the EDA-NOCV method is, that the results of the calculations can not only numerically be expressed but that the impact of the pairwise orbital interactions on the electronic structure can also graphically be visualized. Details of the calculations are given in ESI.‡ For further information about the EDA-NOCV method²³ and recent examples we refer to the literature.²⁴

Table 1 gives the numerical data of the EDA-NOCV calculations of the complex NHC^Me→B₂←NHC^Me for the interactions between the acceptor (3) ¹Σ_g⁺ B₂ (for the choice of the latter excited state of B₂ see ref. 4) and the donor (NHC^Me)₂ at the geometry of the complex. The instantaneous interaction energy ΔE_int = −307.5 kcal mol⁻¹ is very large and overcompensates the electronic excitation energy of B₂ of 106.4 kcal mol⁻¹. The interaction energy ΔE_int comprises the Pauli repulsion ΔE_Pauli (259.0 kcal mol⁻¹) and the binding interactions which comes from the Coulombic attraction ΔE_elstat (−252.3 kcal mol⁻¹) and the covalent (orbital) term ΔE_orb (−314.2 kcal mol⁻¹). The EDA-NOCV calculations suggest that the donor–acceptor bonds NHC^Me→B₂←NHC^Me have a slightly more covalent (55.5%) character than electrostatic character (44.5%).

Table 1 Results of the EDA-NOCV calculations for NHC^Me→B₂←NHC^Me at BP86/TZ2P using the fragments B₂[(3) ¹Σ_g⁺] and (NHC^Me)₂ as interacting species. All energy values in kcal mol⁻¹. Calculated NBO partial charge of B₂ in e

Interacting fragments	B2(NHC^Me)2
	B2[(3) ^1Σg^+] and (NHC^Me)2
a The value in parenthesis gives the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb. b The value in parenthesis gives the percentage contribution to the total orbital interactions ΔEorb.
ΔEint	−307.5
ΔEPauli	259.0
ΔEelstat^a	−252.3 (44.5%)
ΔEorb^a	−314.2 (55.5%)
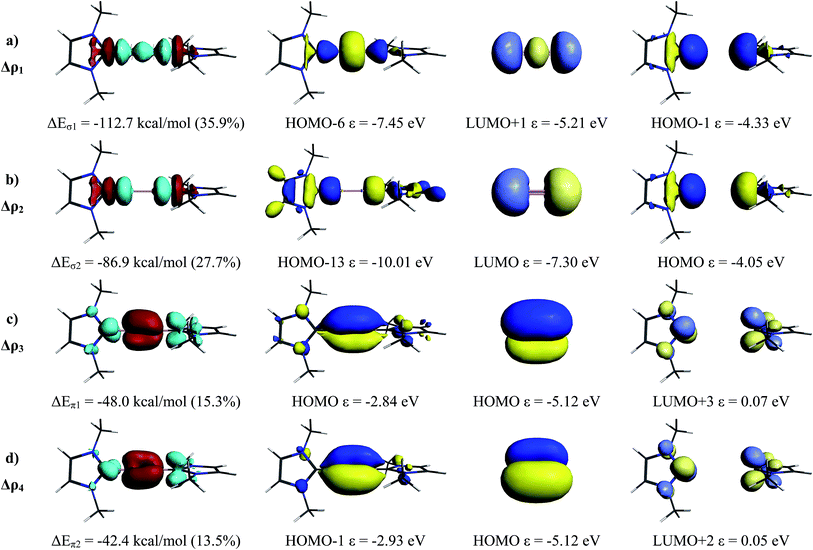
ΔEσ1 L→(B2)←L (+,+) donation^b	−112.7 (35.9%)
ΔEσ2 L→(B2)←L (+,−) donation^b	−86.9 (27.7%)
ΔEπ1 L←(B2)→L π-backdonation^b	−48.0 (15.3%)
ΔEπ2 L←(B2)→L π′-backdonation^b	−42.4 (13.5%)
ΔErest	−24.2 (7.7%)
q(B2)	−0.36

---

The breakdown of the orbital term ΔE_orb into pairwise contributions between occupied and vacant MOs of the fragments provide quantitative insight into the σ-donation NHC^Me→B₂←NHC^Me and π-backdonation NHC^Me←B₂→NHC^Me. The associated charge flow can be visualized through the deformation densities Δρ₁ − Δρ₄ that are shown in Fig. 3, left column. The colour code indicates the direction of the charge flow red→blue. The occupied and vacant orbitals which are connected to the deformation densities are displayed in the three columns at the right side of Fig. 3. There are strongly stabilizing contributions from the in-phase (+,+) NHC^Me→B₂←NHC^Me σ-donation into the LUMO + 1 of (3) ¹Σ_g⁺ B₂ (ΔE_σ1 = −112.7 kcal mol⁻¹) while the out-of-phase (+,−) donation into the energetically lower-lying LUMO is a bit smaller (ΔE_σ2 = −86.9 kcal mol⁻¹) which is due to the better overlap of the former (+,+) donation. There two contributions of the NHC^Me←B₂→NHC^Me π-backdonation are clearly smaller (ΔE_π1 = −48.0 kcal mol⁻¹ and ΔE_π2 = −42.4 kcal mol⁻¹) than the σ-donation. Since both components, σ-donation and π-backdonation significantly contribute to the bonding, a more appropriate notation for the bonding interactions is the formula NHC^Me⇄B≡B⇄NHC^Me. Since the π-backdonation weakens the boron–boron bond, a smaller bond order below 3 but above 2 is expected, which is in agreement with the effective bond order of 2.34 that was derived from the force constants.

Fig. 3 Plot of the interacting donor and acceptor orbitals and calculated eigenvalues ε of (NHC^Me)₂ and (¹Σ_g⁺) B₂ (right two columns) and matching MOs of the complex NHC^Me→B≡B←NHC^Me (second column from the left). Plot of the deformation densities Δρ with connected stabilization energies ΔE of the four most important orbital interactions in B₂(NHC^Me)₂ which indicate the associated charge flow red→blue.

The numerical results of the EDA-NOCV calculations and the graphical display of the deformation densities together with the molecular orbitals provide a bridge between heuristic bonding models of chemistry and a quantum chemical analysis of the electronic structure of the investigated complex. The calculated energy values are not observable data, but they arise from an unambiguously defined partitioning scheme which is not very sensitive to the level of theory. The value of the EDA-NOCV method lies in the fact that it establishes a quantitative classification scheme where comparisons can be made with related compounds. Explanations for experimental findings and predictions for new compounds can be made for different ligands L and atoms E in complexes L→E₂←L as well as for compounds L→E←L by considering the electronic states of E₂ or E and the donor strength of L. This has been shown for numerous complexes of atoms E of group 13,^3,4,6,25 group 14^14,15,26 and group 15.^8c,27 The same approach has recently been used to predict stable beryllium compounds L→Be₂←L.²⁸

We would like to make a comment on the use of the different notations which were used by KS and by us for describing the bonding situation in B₂(NHC^R)₂ (see Scheme 1). The two formulas are not just different writing styles but they refer to different bonding situations between B₂ and the NHC^R moieties. The notation with arrows NHC^Me⇄B≡B⇄NHC^Me indicates heterolytic cleavage of dative bonds while the notation with dashed lines as suggested by KS suggests conjugation over electron-sharing bonds which cleave homolytically. The latter description is appropriate for molecules such as 1,2-butadiene where rupture of the C–C bonds yields radicals. Cleavage of the B–NHC^R bonds gives closed-shell fragments. Recognizing the difference between the two types of bonding has led to the discovery of carbones CL₂ as a peculiar class of organic compounds and related systems which exhibit unusual geometries and reactivities and to the prediction of novel compounds.²⁹

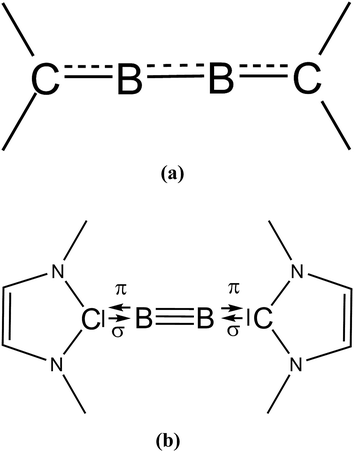Scheme 1 Bonding situation in B₂(NHC)₂ which were suggested (a) by Köppe and Schnöckel and (b) by us.

Finally, we want to point out that two recent papers by Braunschweig just appeared where the strength of the B–B triple bond in the original diboryne B₂(NHC^R)₂ and in the slightly changed species B₂(NHC^R′)₂ with slightly less bulky substituents R′ than R has experimentally been assessed.³⁰ One paper shows that the observed B–B stretching modes of the Raman spectra nicely fit into the established trend of the C≡C and N≡N stretching frequencies of alkynes and dinitrogen.^30a The second paper reports ¹¹B–¹¹B spin–spin (J) coupling constants which indicate that the bonding description in terms of a triple bond is justified.^30b Thus, theory and experiment agree that B₂(NHC^R)₂ contains has significant boron–boron triple bond character.

Summary and conclusion

The results of this work can be summarized as follows. The calculated data and the thorough bonding analysis of the compound B₂(NHC^Me)₂ provide convincing evidence for the appearance of significant boron–boron triple bond character in the model compound and in the isolated diboryne B₂(NHC^R)₂ of Braunschweig which has an even slightly shorter B–B bond. The bonding situation is best described in terms of NHC^Me→B₂←NHC^Me donor–acceptor interactions and concomitant π-backdonation NHC^Me←B₂→NHC^Me which weakens the B–B bond, but the essential features of a triple bond are preserved. An appropriate formula which depicts both interactions is the sketch NHC^Me⇄B≡B⇄NHC^Me.

Calculations of the stretching force F_BB constants which take molecules that have genuine single, double and triple bonds suggest that the effective bond order of B₂(NHC^Me)₂ has the value of 2.34. The suggestion by Köppe and Schnöckel that the strength of the boron–boron bond in B₂(NHC^H)₂ is only between a single and a double bond which should be described with a Lewis structure that has a σ bond and a delocalized π bond is repudiated. It misleadingly takes the force constant F_BB of OBBO as reference value for a B–B single bond which ignores π bonding contributions. The alleged similarity between the B–O bonds in OBBO and the B–C bonds in B₂(NHC^Me)₂ is a mistaken application of the principle of isolable relationship.

Acknowledgements

We appreciate critical and constructive comments of the referees which were very helpful to improve the paper. This work was supported by the Deutsche Forschungsgemeinschaft.

References

1. H. Braunschweig, R. D. Dewhurst, K. Hammond, J. Mies, K. Radacki and A. Vargas, Science, 2012, 336, 1420.
2. P. Pyykkö, S. Riedel and M. Patzschke, Chem.–Eur. J., 2005, 11, 3511.
3. N. Holzmann, A. Stasch, C. Jones and G. Frenking, Chem.–Eur. J., 2011, 17, 13517.
4. N. Holzmann, A. Stasch, C. Jones and G. Frenking, Chem.–Eur. J., 2013, 19, 6467.
5. R. Köppe and H. Schnöckel, Chem. Sci., 2015, 6, 1199.
6. G. Frenking and N. Holzmann, Science, 2012, 336, 1394.
7. An enlightening example for the specific stabilization of NHC via donor–acceptor interactions and the difference to a normal covalent (electron-sharing) bond has been reported: K. C. Mondal, H. W. Roesky, M. C. Schwarzer, G. Frenking, S. Neudeck, I. Tkach, H. Wolf, D. Kratzert, R. Herbst-Irmer, B. Niepötter and D. Stalke, Angew. Chem., Int. Ed., 2013, 52, 1801.
8. (a) A striking example is the phosphane complex N₂(PPh₃) which was synthesized already in 1964, without the bonding situation being recognized: R. Appel and R. Schöllhorn, Angew. Chem., Int. Ed. Engl., 1964, 3, 805; (b) Recent theoretical studies showed that the compound N₂(PPh₃) which melts at 184–186 °C is thermodynamically unstable toward loss of N₂ by ∼90 kcal mol⁻¹: D. J. D. Wilson, S. A. Couchman and J. L. Dutton, Inorg. Chem., 2012, 51, 7657; (c) The high kinetic stability of N₂(PPh₃) could be explained in terms of strong donor–acceptor interactions between the phosphane donor ligands and N₂ in the doubly excited (1) ¹Γ_g state which has a N–N single bond and two lone pairs at each nitrogen atom: N. Holzmann, D. Dange, C. Jones and G. Frenking, Angew. Chem., Int. Ed., 2013, 52, 3004.
9. One referee pointed out that previous theoretical studies showed already that the assignment of a B–B single bond for OBBO is not appropriate: (a) B. Ruscic, C. A. Mayhew and J. Berkowitz, J. Chem. Phys., 1988, 88, 5580; (b) A. V. Neumukhin and F. Weinhold, J. Chem. Phys., 1993, 98, 1329; (c) M. T. Nguyen, M. H. Matus, V. T. Ngan, D. J. Grant and D. A. Dixon, J. Phys. Chem. A, 2009, 113, 4895.
10. (a) A. R. W. McKellar, P. R. Bunker, T. J. Sears, K. M. Evenson, R. J. Saykally and S. R. Langhoff, J. Chem. Phys., 1983, 79, 5251; (b) D. G. Leopold, K. K. Murray and W. C. Lineberger, J. Chem. Phys., 1984, 81, 1048.
11. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711.
12. D. A. Dixon, K. D. Dobbs, A. J. Arduengo III and G. Bertrand, J. Am. Chem. Soc., 1991, 113, 8782.
13. W. A. Herrmann and C. Köcher, Angew. Chem., 1997, 109, 2256 ( Angew. Chem., Int. Ed. Engl. , 1997 , 36 , 2162 ).
14. G. Frenking and R. Tonner, Pure Appl. Chem., 2009, 81, 597.
15. (a) R. Tonner and G. Frenking, Angew. Chem., Int. Ed., 2007, 46, 8695; (b) R. Tonner, G. Heydenrych and G. Frenking, ChemPhysChem, 2008, 9, 1474; (c) W. Petz, F. Öxler, B. Neumüller, R. Tonner and G. Frenking, Eur. J. Inorg. Chem., 2009, 4507.
16. G. E. Hardy, J. I. Zink, W. C. Kaska and J. C. Baldwin, J. Am. Chem. Soc., 1978, 100, 8001.
17. (a) C. A. Dyker, V. Lavallo, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2008, 47, 3206; (b) A. Fürstner, M. Alcarazo, R. Goddard and C. W. Lehmann, Angew. Chem., Int. Ed., 2008, 47, 3210; (c) M. Alcarazo, W. Lehmann, A. Anoop, W. Thiel and A. Fürstner, Nat. Chem., 2009, 1, 295.
18. A. Szabó, A. Kovács and G. Frenking, Z. Anorg. Allg. Chem., 2005, 631, 1803.
19. For a detailed analysis of the nature of the bonding in nonpolar single, double and triple bonds, see: A. Kovács, C. Esterhuysen and G. Frenking, Chem.–Eur. J., 2005, 11, 1813.
20. (a) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933; (b) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962.
21. (a) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755; (b) K. Morokuma, J. Chem. Phys., 1971, 55, 1236.
22. (a) M. P. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576; (b) M. P. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681.
23. G. Frenking and F. M. Bickelhaupt, The Chemical Bond. 1. Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 121–158.
24. See the following paper and references cited therein: P. Jerabek, H. W. Roesky, G. Bertrand and G. Frenking, J. Am. Chem. Soc., 2014, 136, 17123.
25. (a) N. Holzmann and G. Frenking, Croat. Chem. Acta, 2014, 87, 413; (b) R. Kinjo, B. Donnadieu, M. A. Celik, G. Frenking and G. Bertrand, Science, 2011, 333, 610; (c) M. A. Celik, R. Sure, S. Klein, R. Kinjo, G. Bertrand and G. Frenking, Chem.–Eur. J., 2012, 18, 5676.
26. See the following paper and references cited therein: G. Frenking and R. Tonner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 869.
27. M. A. Celik, R. Sure, S. Klein, R. Kinjo, G. Bertrand and G. Frenking, Chem.–Eur. J., 2012, 18, 5676.
28. S. A. Couchman, N. Holzmann, G. Frenking, D. J. D. Wilson and J. L. Dutton, Dalton Trans., 2013, 42, 11375.
29. G. Frenking, Angew. Chem., Int. Ed., 2014, 53, 6040.
30. (a) J. Böhnke, H. Braunschweig, P. Constandinidis, T. Dellermann, W. C. Ewing, I. Fischer, K. Hammond, F. Hupp, J. Mies, H.-C. Schmitt and A. Vargas, J. Am. Chem. Soc., 2015, 137, 1766; (b) F. A. Perras, W. C. Ewing, T. Dellermann, J. Böhnke, S. Ullrich, T. Schäfer, H. Braunschweig and D. L. Bryce, Chem. Sci., 2015, 6, 3378.

---

Footnotes

† This paper is dedicated to Professor Peter Paetzold on the occasion of his 80th birthday.

‡ Electronic supplementary information (ESI) available: Details of the theoretical calculations and coordinates and energies of the calculated molecules. See DOI: 10.1039/c5sc01504a

---