Open Access Article
Open Access ArticleHow important are dispersion interactions to the strength of aromatic stacking interactions in solution?†
Jungwun
Hwang
,
Brent E.
Dial
,
Ping
Li
,
Michael E.
Kozik
,
Mark D.
Smith
and
Ken D.
Shimizu
 *
*
Department of Chemistry and Biochemistry, University of South Carolina, SC 29208, USA. E-mail: shimizu@mail.chem.sc.edu
First published on 18th May 2015
Abstract
In this study, the contributions of London dispersion forces to the strength of aromatic stacking interactions in solution were experimentally assessed using a small molecule model system. A series of molecular torsion balances were designed to measure an intramolecular stacking interaction via a conformational equilibrium. To probe the importance of the dispersion term, the size and polarizability of one of the aromatic surfaces were systematically increased (benzene, naphthalene, phenanthrene, biphenyl, diphenylethene, and diphenylacetylene). After correcting for solvophobic, linker, and electrostatic substituent effects, the variations due to polarizability were found to be an order of magnitude smaller in solution than in comparison to analogous computational studies in vacuo. These results suggest that in solution the dispersion term is a small component of the aromatic stacking interaction in contrast to their dominant role in vacuo.
Introduction
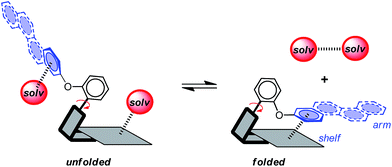
Aromatic stacking interactions play a key role in determining the stability, activity, and utility of many supramolecular processes such as the structure of biopolymers,1–3 host–guest complex stability,4–7 and the selectivity of asymmetric catalysts.8–10 The importance and utility of aromatic stacking interactions have provided the motivation to study the fundamental nature of the interaction and to develop models that can accurately predict their stability trends.11,12 Thus, the influence of variables to the strength of stacking interactions such as charge,13,14 substituent effects,15,16 and solvent effects17,18 has been an active area of research.The goal of this study was to experimentally assess the role that dispersion interactions play in the aromatic stacking interaction in solution using a dynamic small molecule model system (Scheme 1).19–21 Our approach was to systematically vary the size of one of the aromatic surfaces involved in an aromatic stacking interaction. This strategy mirrors that of a computational study by Zeinalipour-Yazdi and Pullman,22 which predicted a dramatic strengthening of the aromatic stacking interaction with increasing size of an aromatic surface due to an increase in the dispersion term.
Attractive London dispersion interactions are weak attractive interactions that can form between both polar and non-polar molecular surfaces.12,23 In the gas-phase, dispersion interactions have been identified as the dominant contributing term for aromatic stacking interactions.24–26 For example, Sherrill's component analysis estimated that the dispersion term comprises 61% of the overall stacking energy for the benzene dimer.27 However, the role of dispersion forces in solution has been much more controversial. Specifically, the dispersion contributions in solution have been proposed to be much smaller.28 The rationale is that there are roughly an equal number of dispersion interactions on either side of the stacking equilibrium (Scheme 1). The aromatic surfaces still form attractive dispersion interactions in the stacking complex. However, solvent molecules form additional dispersion interactions on either side of the binding equilibrium with the uncomplexed aromatic surfaces and with each other.28 Thus, the question is whether the net dispersion interactions on the right-hand side of the equilibrium are stronger than those on the left-hand side of the equilibrium.
The measurement of dispersion interaction in solution has posed a number of experimental challenges.29,30 First, the dispersion contributions are expected to be small, and thus a very sensitive method with sub kcal mol−1 accuracy is required. Second, in contrast to electrostatic or solvent trends, it is difficult to systematically vary the dispersion term of a non-covalent interaction. Third, dispersion interactions are very difficult to differentiate from solvophobic interactions because both scale with increasing size of the aromatic surfaces.31,32 Thus, studies that have observed a correlation between the size of the aromatic surface and the strength of the stacking interaction could be attributed to solvophobic or dispersion effects.33–35
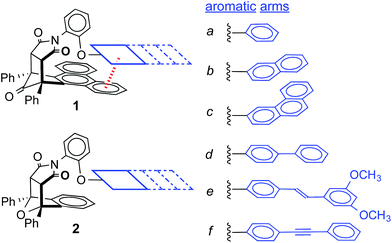
In this study, a small molecule model system was designed to specifically address the above challenges.36,37 First, the model system is an example of a “molecular torsion balance”, which has been demonstrated to provide a very accurate and sensitive measure of non-covalent interactions.37 Variations in the strength of the intramolecular interaction as small as ±0.03 kcal mol−1 can be measured by monitoring their influence on the folded-unfolded equilibrium (Scheme 1).38–41 Second, the dispersion term was systematically varied by increasing the conjugation length and polarizability of one of the interacting surfaces. Dispersion interactions are known to increase with increasing molecular polarizability because dispersion interactions are the result of the electrostatic attraction between polarizable molecular surfaces.22,42,43 Third, the dispersion effects were differentiated from the solvophobic effects by keeping the contact area between the two stacking aromatic surfaces constant. The rigid bicyclic framework of the molecular balances fixes the geometry and contact area of the aromatic surfaces in 1a–f (Fig. 2a). Only the first benzene ring of the aromatic arm, regardless of its size, was in contact with the phenanthrene shelf. Thus, the extended aromatic surfaces in 1b–f did not form any additional stacking or solvophobic interactions.
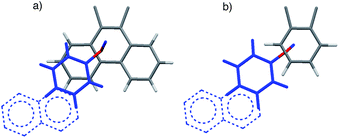 | ||
| Fig. 2 Top views of the aromatic arm (colored blue) and shelf (colored gray) surfaces in the folded conformers of the (a) balance 1a and (b) control balance 2a. The models are based on the crystal structures of an analogue of 1a41 and DFT molecular modelling (M06-2X, 6-31G*)46 for 2a. For viewing clarity, only the aromatic surfaces of the arm and shelf are shown. The extrapolated extended surfaces in arms of b and d are depicted as dotted lines. | ||
An additional advantage of these molecular systems was that the results could be directly compared with computational studies.22,40,44 These computational studies provided theoretical in vacuo benchmarks to compare the magnitudes of our experimentally measured trends in solution. The most similar computational studies were by Zeinalipour-Yazdi and Pullman, which measured the stacking energy of a benzene with aromatic surfaces of varying size.22 The molecular balances performed an analogous comparison as the outer most benzene ring of the phenanthrene shelf forms stacking interactions with the aromatic arms of varying size. In the computational studies, the stacking energies of the benzene unit were found to systematically increase with the increasing size and polarizability of the opposing aromatic surface. A steep linear correlation was predicted between the size of the opposing aromatic surfaces and the stacking energies. This trend is consistent with the dispersion term representing a significant portion of the stacking energy in vacuo. For example, the stacking interaction energy of the benzene–naphthalene complex was 2.3 times larger than the benzene–benzene complex. Similarly, the stacking interaction energy of the benzene–anthracene complex was 3.9 times larger than the benzene–benzene complex.
Results and discussion
Molecular balance design
The rigid bicyclic N-arylimide framework of the molecular balances utilized in this study had been previously employed to study a range of non-covalent interactions such as aromatic stacking, CH–π, and cation–π interactions.38–41 In particular, substituted derivatives of balances 1a were able to accurately measure small differences in the aromatic stacking interactions (<0.05 kcal mol−1) due to substituent effects.45 For the measurement of weak non-covalent interactions, this molecular balance framework has a number of attractive features. First, restricted rotation of the N-arylimide rotor leads to the formation of distinct folded and unfolded conformers that are in equilibrium at room temperature. Second, the bicyclic framework holds the aromatic surfaces of the arm and shelf at different distances in the two conformers. In the folded conformer, the arm and shelf surfaces are in close proximity allowing formation of an intramolecular off-set stacking interaction. In the unfolded conformer, the arm and shelf surfaces are held apart and cannot form a stacking interaction. Thus, the folded/unfolded equilibrium ratio provides a very sensitive measure of variations in the strength of the intramolecular interactions. A strengthening of the intramolecular stacking interactions is evident by a shift in the folded/unfolded ratio towards the folded conformer.We have previously demonstrated that the parent balance 1a with a phenyl arm forms a well-defined off-set stacking interaction in the folded conformer (Fig. 2a).40,41 X-ray and NMR analyses of 1a found that the phenyl arm and phenanthrene shelf adopt a parallel stacking geometry in the folded conformer. The phenyl ring of the arm is in contact with outer most ring of the phenanthrene shelf with an arm centroid-to-shelf plane of 3.75 Å. Furthermore, the proximity of the arm and shelve surfaces and the rigidity of the bicyclic framework do not provide sufficient freedom and space to form the alternative arene–arene geometries such as the perpendicular edge-to-face and T-shaped geometries. The rigidity of the balance framework also ensures that the extended aromatic surfaces of the arms in balances 1b–f (represented as dotted lines in Fig. 2a) should not form additional stacking interactions with the phenanthrene shelf. In addition, the contact area between the arm and shelf surfaces should remain constant despite the variations in the size of the aromatic arms.
We have also confirmed that the parent control balance 2a with the phenyl arm is unable to form an intramolecular stacking interaction in the folded conformer due to its shorter benzene shelf (Fig. 2b).41 The absence of stacking interactions in 2a was confirmed by NMR and modeling studies. Thus, control balances 2a–f should provide a measure of the other factors that influence the folded-unfolded equilibria such as solvent, dipole, linker, and secondary interaction effects. The subtraction of the folding energy of 2 from the folding energy of 1 should isolate the intramolecular stacking energy.
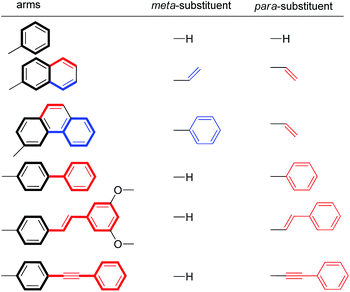
For this study, six balances (1a–f) and six control balances (2a–f) were prepared via previously described synthetic routes.40,41 The six aromatic arms (a–f) include aromatic surfaces of varying size, conjugation length, and polarizability. These aromatic surfaces fell into three groups (Fig. 1). The first was the unsubstituted phenyl arm (a) that had the smallest common aromatic surface. The next were the fused aromatic surfaces with naphthyl and phenanthryl arms (b and c). The last group was the non-fused aromatic surfaces (d–f). These include the biphenyl (d), stilbene (e), and diphenylethynyl (f) arms, which extend the conjugation of the parent phenyl ring from a single substitution point at the para-position.
Verification and measurement of the intramolecular stacking interactions
The formation of the expected intramolecular stacking interactions within the new balances 1b–f was established by comparison of their 1H NMR spectra (CDCl3, 298 K) with those of the parent balance 1a and control balances 2a–f. The NMR analyses were facilitated by a separate set of peaks for the folded and unfolded conformers due to slow exchange on the NMR time scale. The first indication of stacking interactions in 1b–f was the observation of the expected upfield shifts of the aromatic arm and shelf protons. Due to the proximity of the arm and shelf aromatic surfaces in the stacked structure, upfield shifts of up to 1.0 ppm were observed in the folded versus the unfolded conformers. The direction and magnitude of these peak shifts were identical to those observed in the parent stacking phenyl balance 1a.41 By comparison, these same aromatic protons did not display upfield shifts in the folded versus unfolded conformers of control balances 2a–f, which cannot form intramolecular stacking interactions.The formation of stacking interaction was also evident from a comparison of their folding energies. The folded/unfolded ratios of 1a–f and 2a–f and their corresponding folding energies were measured from their peak areas in the 1H NMR spectra (Table 1). The folding energies of the stacking balances 1a–f were consistently stronger (more negative) than the folding energies of the corresponding control balances 2a–f. This was consistent with the stabilization of the folded conformers of 1a–f by the formation of attractive stacking interactions. The intramolecular stacking interactions were estimated from the difference in the folding energies of 1a–f and 2a–f (ΔΔG1–2). The stacking energies ranged from −0.92 to −1.33 kcal mol−1, which were comparable with previous measurements of stacking interactions of benzene surfaces in organic solution.15 Next, the influence of the different sized aromatic arms on the stacking energies was examined. This analysis suggested that the dispersion contributions to the stacking interaction are not dominant in solution. These conclusions were based on two observations. First, the stacking energies in 1a–f were very similar despite the large variations in size of the arm surfaces. The ΔΔG1–2 values spanned a relatively narrow range from −0.92 to −1.33 kcal mol−1. Overall, these variations were an order of magnitude smaller than those predicted by the computational studies.22 For example, the stacking interaction energy of the naphthyl arm in 1b was only 26% greater than the phenyl arm in 1a (−1.16 versus −0.92 kcal mol−1). By comparison, the computational studies predicted a 230% increase in the stacking energies of naphthalene versus benzene surfaces.22
| Arm | ΔG1a | ΔG2a | ΔΔG1–2b | α | ESEd | ΔΔG1–2 − ESEe |
|---|---|---|---|---|---|---|
| a Folding energies (kcal mol−1) measured in CDCl3 at 298 K from the 1H NMR measurement of the folding ratios with an error of ±0.03 kcal mol−1. b Difference in folding energies (kcal mol−1) of balances 1 and 2 with an error of ±0.04 kcal mol−1. c Polarizabilities calculated for the aromatic arm surfaces using Spartan10 (B3LYP, 6-31G*), with units of a.u.3 d The estimated electrostatic substituent effect (ESE) based on the Hammett σmeta parameters and the previously measured ESE for the parent balance 1a.45 See Table S5 and Fig. S19 in the ESI. e Stacking energy corrected for the electrostatic substituent effect with units of kcal mol−1 and an error of ±0.04 kcal mol−1. | ||||||
| a | 0.48 | 1.40 | −0.92 | 48 | 0.00 | −0.92 |
| b | 0.17 | 1.33 | −1.16 | 52 | −0.22 | −0.93 |
| c | −0.08 | 1.26 | −1.33 | 57 | −0.22 | −1.11 |
| d | 0.31 | 1.41 | −1.10 | 55 | 0.00 | −1.11 |
| e | 0.38 | 1.33 | −0.95 | 62 | 0.02 | −0.97 |
| f | 0.29 | 1.33 | −1.05 | 57 | −0.04 | −1.01 |
Second, no clear correlation was observed between the stacking energies and the polarizabilities of the respective arms. The polarizabilities of the aromatic surfaces in the arms were estimated using computational methods (B3LYP, 6-31G*) (Table 1).47 The most polarizable arms such as the diphenyl acetylene and stilbene did not show the strongest stacking energies. More convincingly, a plot of the calculated polarizabilities versus the measured stacking energies (ΔΔG1–2) did not show a clear correlation (Fig. 3). The stacking energies of the different sized arms appeared to strengthen (more negative) with increasing polarizability of the fused arms (b and c). However, an inverse correlation was observed between polarizability and stacking energy for the non-fused arm (d–f).
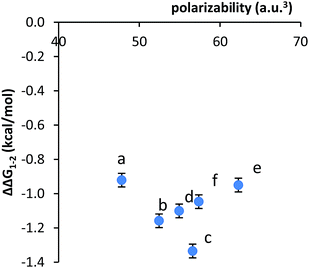 | ||
| Fig. 3 Plot of the correlation between the measured stacking energies (ΔΔG1–2) in balance 1a–f and the polarizability of the aromatic arms a–f. | ||
Explanations for the inability to observe the dispersion contributions to the stacking energy trends
The inability to observe the dispersion of the stacking interaction energies in solution was consistent with the hypothesis that the dispersion contributions would be smaller in solution because of the counter-balancing dispersion interactions of the solvent molecules. However, alternative explanations were also explored. First, the possibility was that the variations in the stacking energies were within the error for the measurement. The standard deviation of the stacking energies was 0.15 kcal mol−1. While this value is small, it is greater than the error for the analysis which was estimated to be ±0.04 kcal mol−1.The second possible explanation was that the variations in the stacking energies were due to electrostatic substituent effects (ESEs). Substituents on aromatic rings have been shown to stabilize and destabilize the aromatic stacking interaction in computational and experimental studies.15,16,48–50 Along these lines, we have previously characterized the electrostatic substituent effects (ESE) of this specific stacking model system.45 This allowed us to estimate the influence of the substituent effects and to test whether the substituent effects can explain the observed minor variations in stacking interaction energies.
To assess the ESEs in this system, the extended conjugation of arms b–f was classified as meta- and/or para-substituents on the core phenyl arm a (Table 2). Arms d–f were treated as monosubstituted phenyl rings. For example, the biphenyl arm in balance 1d was categorized as a phenyl ring with a para-phenyl substituent. The fused naphthyl and phenanthryl arms b and c were treated as disubstituted phenyl rings with one meta- and one para-substituent. The expected stabilizing or destabilizing ESEs were calculated based on the Hammett σmeta parameters for respective substituents in Table 2 and the slopes of the previously measured Hammett plots for this balance system.51 The details of this calculation are provided in the ESI.† For the disubstituted arms (b and c), the ESEs were calculated as the sum of the individual substituent effects. This analysis is based on the recent finding that the substituent effects for stacking interactions are additive.45
The estimated ESEs were able to explain half of the variation in the ΔΔG1–2 values. The ESEs for arms b–f were mostly stabilizing, which was consistent with the observed stronger stacking energies for the extended arms b–f. The vinyl, phenyl, styrene, and phenylacetylene substituents in the arms are all weak electron withdrawing groups with small positive Hammett σmeta values (0.03 to 0.14). Electron withdrawing substituents have been shown to stabilize stacking interactions due to the formation of attractive electrostatic interactions.52 To assess the importance of the substituent effects, the predicted ESE values were subtracted from the measured ΔΔG1–2 values to give a substituent corrected stacking energy (ΔΔG1–2 − ESE). The corrected stacking energies (−0.92 to −1.11 kcal mol−1) had approximately half the variation than the uncorrected stacking energies (−0.92 to −1.33 kcal mol−1).
The third alternative explanation that was examined was that the substituent effects had been obscuring the smaller dispersion effects. To test this possibility, the correlation between the substituent corrected stacking energies and polarizability was examined (Fig. 4). The plot of ΔΔG1–2 − ESE versus polarizability was relatively flat, as the majority of variance had been removed. However, the remaining variance did not show a correlation with the polarizabilities of the aromatic surfaces.
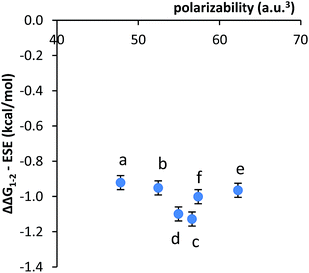 | ||
| Fig. 4 Plot of the correlation between the substituent effects corrected stacking energies (ΔΔG1–2 − ESE) and the polarizability of the aromatic arms a–f. | ||
The final explanation for the inability to observe the dispersion effects was that the experimental design has not properly isolated the stacking energy from the folded-unfolded equilibrium energies. Of particular concern were solvophobic effects, which have been cited as the dominant term for the weak non-covalent interactions of non-polar surfaces in solution.53,54 However, there were two observations that suggested that solvent and solvophobic effects had been effectively isolated in this study. First, relatively small differences in the stacking energies in 1a–f were observed despite the large variation in the size of the aromatic arms. Thus, the geometric constraints in the balance framework appear to have been effective in keeping the surface area contact and solvophobic effects constant for the series. Second, the folding energies of balances 1a–f and 2a–f were measured in two additional solvent systems. The folding energies of balances 1a–f and control balances 2a–f were measured in a more polar, acetone-D6, and a less polar, bromobenzene-D5, solvent (see ESI†). The overall trends and conclusions were analogous to those observed in CDCl3, suggesting that the solvent effects were not the reason for the inability to observe dispersion effects. The uncorrected (ΔΔG1–2) and corrected (ΔΔG1–2 − ESE) stacking energies in these two additional solvents had relatively small variations and did not show any clear correlation with the polarizabilities of the aromatic surfaces (ESI Fig. S22 and 23†).
Conclusions
In this study, we designed a series of molecular torsion balances 1a–f to assess the importance of dispersion interactions to the aromatic stacking interactions in solution. These model systems measured the strength of an intramolecular stacking interaction via changes in a folded-unfolded conformational equilibrium. The contribution of the dispersion term was assessed by systematically varying the size and polarizability of one of the aromatic surfaces and measuring the effect on the stacking energies. Through the use of control systems 2a–f, geometrical constraints, and studies in multiple solvents, the stacking interaction energies were separated from other factors that influence the conformational equilibrium such as solvophobic, dipole, linker, and steric effects.No correlation was observed between the polarizabilities of the aromatic surfaces and the stacking energies. There was relatively little variance in the strengths of the stacking energies despite the wide range in the sizes and conjugation lengths of the aromatic surfaces. These results suggest that the dispersion contributions to the aromatic stacking interaction in solution are relatively minor.
The approach and conclusions of this study nicely complement studies of the origins of alkyl–alkyl interactions in solution.53 Cockroft and co-workers used a perpendicular approach of assessing the contributions of dispersion interactions in solution. Instead of varying the size and polarizability of the interacting surfaces, they systematically varied the solvent environment, which allowed them to measure and subtract out the solvent effects from the overall interaction energy. Although the approach was different, the conclusions were similar to those in this study as the dispersion term of the interaction could not be observed in solution. The majority of the interaction energy was attributed to the solvent and solvophobic effects. A more recent study by Cockroft was able to measure the dispersion contributions to the interaction energy of non-polar surfaces in organic solution. However, the dispersion terms in non-polar organic solvents were small and were on the same order as the solvophobic interactions.55
The conclusion that dispersion interactions do not play a dominant role in stacking interactions in solution is in contrast to computational studies, which have found a dramatic correlation between the stacking energy versus the size and polarizability of an aromatic surface.22 It is important to note that the smaller influences of dispersion interactions in solution is not due to an absence of dispersion interactions. Aromatic surfaces still form attractive dispersion interactions in solution just as they do in vacuo. However, the aromatic surfaces also form dispersion interactions with solvent molecules, which attenuates the overall magnitude of the dispersion term.
Experimental section
Synthesis of balances 1a–f and control balances 2a–f
Balance 1a–f and control balance 2a–f were synthesized as previously described.41 The balances and control balances were prepared by the following general route. First, the phenol corresponding to the arm was reacted with 2-fluoronitrobenzene in an SNAr reaction that formed the diphenyl ether. The nitro-ether was reduced to the amino-ether and then reacted with the endo-bicyclic anhydride to yield the balance or control balance. Specific procedures and characterization data for 1a–f and 2a–f are provided in the ESI.†Measurement of the folding energies
The folded/unfolded ratios were measured by integration of the 1H NMR spectra at 25 °C. The peak areas of the singlets corresponding to the succinimide methine protons were measured by line fitting analysis. The folding energies were calculated from the equation ΔG = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln([folded]/[unfolded]). The error in the folding energies was estimated to be ±0.03 kcal mol−1 based on a conservative estimate of the NMR measured folded/unfolded ratio of ±5%.57
ln([folded]/[unfolded]). The error in the folding energies was estimated to be ±0.03 kcal mol−1 based on a conservative estimate of the NMR measured folded/unfolded ratio of ±5%.57
Acknowledgements
This work was supported by the National Science Foundation Grants CHE 1310139 and CHE 1112431.Notes and references
- K. E. Riley and P. Hobza, Acc. Chem. Res., 2013, 46, 927–936 CrossRef CAS PubMed.
- E. T. Kool, J. C. Morales and K. M. Guckian, Angew. Chem., Int. Ed., 2000, 39, 990–1009 CrossRef CAS.
- B. Heddi and A. T. Phan, J. Am. Chem. Soc., 2011, 133, 9824–9833 CrossRef CAS PubMed.
- F. G. Klarner and B. Kahlert, Acc. Chem. Res., 2003, 36, 919–932 CrossRef PubMed.
- T. H. Webb and C. S. Wilcox, Chem. Soc. Rev., 1993, 22, 383–395 RSC.
- M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438 CrossRef CAS PubMed.
- M. Harmata, Acc. Chem. Res., 2004, 37, 862–873 CrossRef CAS PubMed.
- A. Erkkila, I. Majander and P. M. Pihko, Chem. Rev., 2007, 107, 5416–5470 CrossRef PubMed.
- H. C. Kolb, M. S. Vannieuwenhze and K. B. Sharpless, Chem. Rev., 1994, 94, 2483–2547 CrossRef CAS.
- E. H. Krenske and K. N. Houk, Acc. Chem. Res., 2013, 46, 979–989 CrossRef CAS PubMed.
- E. C. Lee, D. Kim, P. Jurecka, P. Tarakeshwar, P. Hobza and K. S. Kim, J. Phys. Chem. A, 2007, 111, 3446–3457 CrossRef CAS PubMed.
- S. Ehrlich, J. Moellmann and S. Grimme, Acc. Chem. Res., 2013, 46, 916–926 CrossRef CAS PubMed.
- S. Yamada and J. S. Fossey, Org. Biomol. Chem., 2011, 9, 7275–7281 CAS.
- K. Kano, H. Minamizono, T. Kitae and S. Negi, J. Phys. Chem. A, 1997, 101, 6118–6124 CrossRef CAS.
- B. W. Gung, X. W. Xue and H. J. Reich, J. Org. Chem., 2005, 70, 3641–3644 CrossRef CAS PubMed.
- S. L. Cockroft, J. Perkins, C. Zonta, H. Adams, S. E. Spey, C. M. R. Low, J. G. Vinter, K. R. Lawson, C. J. Urch and C. A. Hunter, Org. Biomol. Chem., 2007, 5, 1062–1080 CAS.
- M. S. Cubberley and B. L. Iverson, J. Am. Chem. Soc., 2001, 123, 7560–7563 CrossRef CAS PubMed.
- T. Rehm and C. Schmuck, Chem. Commun., 2008, 801–813 RSC.
- M. L. Waters, Curr. Opin. Chem. Biol., 2002, 6, 736–741 CrossRef CAS PubMed.
- J. Sponer, K. E. Riley and P. Hobza, Phys. Chem. Chem. Phys., 2008, 10, 2595–2610 RSC.
- L. M. da Costa, S. R. Stoyanov, S. Gusarov, P. R. Seidl, J. W. D. Carneiro and A. Kovalenko, J. Phys. Chem. A, 2014, 118, 896–908 CrossRef PubMed.
- C. D. Zeinalipour-Yazdi and D. P. Pullman, J. Phys. Chem. B, 2006, 110, 24260–24265 CrossRef CAS PubMed.
- P. Hobza and J. Sponer, Chem. Rev., 1999, 99, 3247–3276 CrossRef CAS PubMed.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104–112 CrossRef CAS PubMed.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200–10207 CrossRef CAS.
- R. L. Jaffe and G. D. Smith, J. Chem. Phys., 1996, 105, 2780–2788 CrossRef CAS.
- C. D. Sherrill, Acc. Chem. Res., 2013, 46, 1020–1028 CrossRef CAS PubMed.
- C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS PubMed.
- H. J. Schneider, Angew. Chem., Int. Ed., 2009, 48, 3924–3977 CrossRef CAS PubMed.
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 651–669 RSC.
- R. R. Gardner, L. A. Christianson and S. H. Gellman, J. Am. Chem. Soc., 1997, 119, 5041–5042 CrossRef CAS.
- Z. Chen, A. Lohr, C. R. Saha-Moller and F. Wurthner, Chem. Soc. Rev., 2009, 38, 564–584 RSC.
- L. Sebaoun, V. Maurizot, T. Granier, B. Kauffmann and I. Huc, J. Am. Chem. Soc., 2014, 136, 2168–2174 CrossRef CAS PubMed.
- P. Jonkheijm, F. J. M. Hoeben, R. Kleppinger, J. van Herrikhuyzen, A. P. H. J. Schenning and E. W. Meijer, J. Am. Chem. Soc., 2003, 125, 15941–15949 CrossRef CAS PubMed.
- P. F. Duan and M. H. Liu, Langmuir, 2009, 25, 8706–8713 CrossRef CAS PubMed.
- S. Paliwal, S. Geib and C. S. Wilcox, J. Am. Chem. Soc., 1994, 116, 4497–4498 CrossRef CAS.
- I. K. Mati and S. L. Cockroft, Chem. Soc. Rev., 2010, 39, 4195–4205 RSC.
- C. Zhao, R. M. Parrish, M. D. Smith, P. J. Pellechia, C. D. Sherrill and K. D. Shimizu, J. Am. Chem. Soc., 2012, 134, 14306–14309 CrossRef CAS PubMed.
- W. R. Carroll, C. Zhao, M. D. Smith, P. J. Pellechia and K. D. Shimizu, Org. Lett., 2011, 13, 4320–4323 CrossRef CAS PubMed.
- P. Li, C. Zhao, M. D. Smith and K. D. Shimizu, J. Org. Chem., 2013, 78, 5303–5313 CrossRef CAS PubMed.
- W. R. Carroll, P. Pellechia and K. D. Shimizu, Org. Lett., 2008, 10, 3547–3550 CrossRef CAS PubMed.
- P. Hobza, H. L. Selzle and E. W. Schlag, J. Am. Chem. Soc., 1994, 116, 3500–3506 CrossRef CAS.
- M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, J. Am. Chem. Soc., 2002, 124, 10887–10893 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS PubMed.
- J. Hwang, P. Li, W. R. Carroll, M. D. Smith, P. J. Pellechia and K. D. Shimizu, J. Am. Chem. Soc., 2014, 136, 14060–14067 CrossRef CAS PubMed.
- J. Gu, J. Wang, J. Leszczynski, Y. Xie and H. F. Schaefer, Chem. Phys. Lett., 2008, 459, 164–166 CrossRef CAS.
- Calculated polarizabilities were used for the analysis because values for the molar refractivities (MR) of all of the aromatic arm surfaces were not available. The calculated polarizabilities were shown to linearly correlate with the MR for aromatic surfaces, which had literature MR values (see ESI Fig. S18†).
- S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855 CrossRef CAS PubMed.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2003, 107, 8377–8379 CrossRef CAS.
- B. W. Gung, M. Patel and X. W. Xue, J. Org. Chem., 2005, 70, 10532–10537 CrossRef CAS PubMed.
- The Hammett σmeta parameter was used to characterize the ESE meta- and para-substituents. The reason is that the σmeta parameter gives a ‘purer’ measure of the inductive electrostatic substituent effects. The σpara parameter also includes resonance substituent effects. The para- and meta-substituent effects were differentiated based on the use of separate measured Hammett plots to characterize the magnitude of the ESEs.
- S. L. Cockroft, C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Am. Chem. Soc., 2005, 127, 8594–8595 CrossRef CAS PubMed.
- L. Yang, C. Adam, G. S. Nichol and S. L. Cockroft, Nat. Chem., 2013, 5, 1006–1010 CrossRef CAS PubMed.
- D. B. Smithrud and F. Diederich, J. Am. Chem. Soc., 1990, 112, 339–343 CrossRef CAS.
- C. Adam, L. Yang and S. L. Cockroft, Angew. Chem., Int. Ed., 2015, 54, 1164–1167 CrossRef CAS PubMed.
- C. F. R. A. C. Lima, M. A. A. Rocha, L. R. Gomes, J. N. Low, A. M. S. Silva and L. M. N. B. F. Santos, Chem. - Eur. J., 2012, 18, 8934–8943 CrossRef CAS PubMed.
- M. Bauer, A. Bertario, G. Boccardi, X. Fontaine, R. Rao and D. Verrier, J. Pharm. Biomed. Anal., 1998, 17, 419–425 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details; X-ray and 1H/13C NMR data; details of substituent effect analyses and solvent studies. CCDC 1058828-1058830. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc01370d |
| This journal is © The Royal Society of Chemistry 2015 |