Isomerisation of nido-[C₂B₁₀H₁₂]²⁻ dianions: unprecedented rearrangements and new structural motifs in carborane cluster chemistry

Abstract

Dianionic nido-[C₂B₁₀]²⁻ species are key intermediates in the polyhedral expansion from 12- to 13-vertex carboranes and metallacarboranes, and the isomer adopted by these nido intermediates dictates the isomeric form of the 13-vertex product. Upon reduction and metallation of para-carborane up to five MC₂B₁₀ metallacarboranes can be produced (Angew. Chem., Int. Ed., 2007, 46, 6706), the structures of which imply the intermediacy of 1,7-, 3,7-, 4,7-, 7,9- and 7,10-isomers of the nido-[C₂B₁₀]²⁻ species. In this paper we use density functional theory (DFT) calculations to characterise the reduction of closo-C₂B₁₀H₁₂ carboranes and the subsequent isomerisations of the nido-[C₂B₁₀H₁₂]²⁻ dianions. Upon reduction para-carborane initially opens to [1,7-nido-C₂B₁₀H₁₂]²⁻ (abbreviated to 1,7) and [4,7-nido-C₂B₁₀H₁₂]²⁻ (4,7) and isomerisation pathways connecting 1,7 to 7,9, 4,7 to 7,10 and 1,7 to 3,7 have been characterised. For ortho- and meta-carborane the experimental reduction produces 7,9 in both cases and computed pathways for both processes are also defined; with ortho-carborane rearrangement occurs via7,8, whereas with meta-carborane 7,9 is formed directly. The 7,9 isomer is the global minimum nido-structure. The characterisation of these isomerisation processes uncovers intermediates that adopt new structural motifs that we term basket and inverted nido. Basket intermediates feature a two-vertex basket handle bridging the remaining 10 vertices; inverted nido intermediates are related to known nido species, in that they have 5- and 6-membered belts, but where the latter, rather than the former, is capped, leaving a 5-membered open face. These new intermediates exhibit similar stability to the nido species, which is attributed to their relation to the 13-vertex docosahedron through the removal of 5-connected vertices. Isomerisation pathways starting from nido geometries are most often initiated by destabilisation of the cluster through a DSD process causing the 3-connected C⁷ vertex to move into a 4-connected site and a neighbouring B vertex to become 3-connected. The ensuing rearrangement of the cluster involves processes such as the pivoting of a 4-vertex diamond about its long diagonal, the pivoting of two 3-vertex triangles about a shared vertex and DSD processes. These processes are all ultimately driven by the preference for carbon to occupy low-connected vertices on the open 6-membered face of the resulting nido species.

---

Introduction

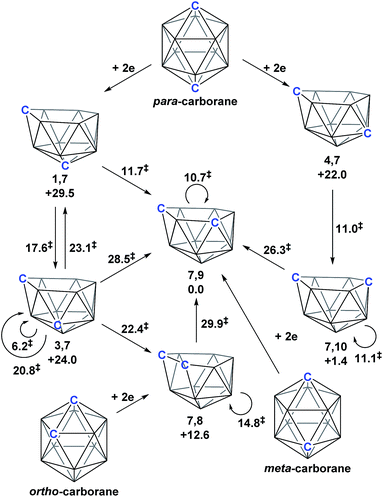
As predicted by Wade's Rules,¹ the addition of a skeletal electron pair (SEP) to a closo polyhedron (with [n + 1] SEPs, where n is the number of vertices) results in the formation of the corresponding nido cluster ([n + 2] SEPs). A key synthetic route that relies upon this is the polyhedral expansion method, whereby 2-electron reduction of a closo precursor (normally a 12-vertex carborane) results in the formation of a nido fragment, which can then be capitated with a {BR} or {M} fragment. Application of this method led to both the first 13-vertex metallacarborane² and the first 13-vertex carborane.³ In 2007 we showed that the polyhedral expansion of a single carborane precursor, [1,12-Ph₂-1,12-closo-C₂B₁₀H₁₀], with {M} = {Ru(p-cymene)} led to the formation of five isomeric supraicosahedral metallacarboranes of the form RuC₂B₁₀ (Fig. 1).⁴ This implies the presence of five isomeric nido fragments following reduction, i.e.1,7-, 3,7-, 4,7-, 7,9- and [7,10-Ph₂-7,10-nido-C₂B₁₀H₁₀]²⁻. A concurrent computational study on [1,12-closo-C₂B₁₀H₁₂] (para-carborane) suggested the first nido-fragments formed upon reduction were [1,7-nido-C₂B₁₀H₁₂]²⁻ (termed 1,7 in the following) and [4,7-nido-C₂B₁₀H₁₂]²⁻ (4,7). At the time, the further isomerisation of these species to the remaining nido species was not considered, however computing these directly provided relative energies, H (enthalpies, 0 K) of +29.5, +24.0, +22.0 and +1.4 kcal mol⁻¹ for 1,7, 3,7, 4,7 and 7,10 respectively, all relative to 7,9 at 0.0 kcal mol⁻¹. In contrast, related experimental studies adopting ortho- or meta-carborane precursors show that 7,9 is the only nido species formed.^2,5–7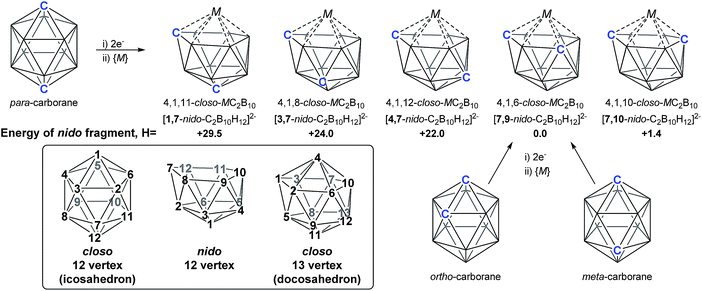

Fig. 1 Results of polyhedral expansion of 12-vertex carboranes to 13-vertex metallacarboranes. For para-carborane {M} = {Ru(p-cymene)}, {C} = {CPh} relating to ref. 4; for ortho-carborane, e.g. {M} = {Ru(p-cymene)} or {CoCp}, {C} = e.g. {CH}.^2,5 Computed energies of [nido-C₂B₁₀H₁₂]²⁻ species given relative to 7,9 in kcal mol⁻¹. See inset for formal numbering.

The thermal rearrangement of 12-vertex closo (hetero)boranes has been the subject of continued investigation. Starting from ortho-carborane, the conversion to meta-carborane at 450 °C and then to para-carborane at 700 °C has been known for over 50 years and indeed was the route to their first syntheses.^8–10 The processes involved in their rearrangement have been studied for many years, both theoretically^11–16 and experimentally through labelling studies.^17–19 In 1966, Lipscomb¹³ introduced the diamond-square-diamond (DSD) mechanism (Scheme 1a), while in the same year, Zakharkin and Kalinin¹⁶ suggested the triangular face rotation (TFR) mechanism, which can also be described as three concerted DSD processes (Scheme 1b). The DSD process in particular has since been recognised as key to carborane rearrangement. Wales¹⁵ adopted an eigenvector following method to map the potential energy surface of C₂B₁₀H₁₂ at the Hartree–Fock (HF) level. Multi-step DSD-derived processes were found to dominate, however two TFR-type pathways were also located. High symmetry processes involving multiple simultaneous DSDs (e.g. the hextuple DSD process leading to a cuboctahedral geometry suggested by Lipscomb¹³) were discounted due to their unfeasibly high activation energies. Later studies also demonstrate an energetic preference for low symmetry processes.^11,12,14 Wales also ruled out the closo-nido-closo rearrangement pathway, which requires opening of the cage to a high energy pseudo-nido intermediate.

Scheme 1 Neutral (hetero)borane isomerisation processes (a) DSD and (b) TFR.

More recently, Brown and McKee¹¹ showed, through density functional theory (DFT) calculations, that a single step TFR process was favoured in the ortho- to meta-carborane isomerisation, while a two-step DSD pathway was preferred for isomerisation from meta- to para-carborane. Brown and McKee had discounted a two-step pathway from ortho- to meta-carborane, due to a high initial barrier between ortho-carborane and the intermediate involved. We later showed that the equivalent intermediate was formed upon the oxidation of 7,9 and characterised a lower energy process to form ortho-carborane, in agreement with experiment.¹² Most recently, Sugden and co-workers¹⁴ investigated both of these isomerisation pathways through ab initio molecular dynamics (DFT-MD) adopting the PBE functional.

In stark contrast, few computational studies have involved reduced 12-vertex carboranes, despite the isomeric form of the reduced species ultimately dictating the isomer of the supraicosahedral product. McKee et al.²⁰ computed 7,9 directly, through HF calculations, for comparison with plausible protonated [nido-C₂B₁₀H₁₃]⁻ structures. Later, Hermansson and co-workers²¹ showed in a study of the electron affinities of carboranes (also at the HF level) that sequential addition of two electrons to meta-carborane resulted in 7,9, while geometries produced from reduction of ortho- and para-carborane showed only minor distortions and did not resemble nido fragments. More recently, 12-vertex nido carboranes and (bis)carboranes have featured in our investigations of the aforementioned oxidation of 7,9 to ortho-carborane,¹² the room-temperature C–C activation of an arene at a 13-vertex metallacarborane,²² co-production of isomeric 13-vertex cobaltacarboranes from polyhedral expansion of a tethered carborane precursor²³ and in the rational design of derivatives of 7,9 stabilised towards aerial oxidation.²⁴

Herein we report a computational study of the isomerisation processes that follow from the initial 2e reduction of para-carborane and formation of 1,7 and 4,7, revealing pathways interconnecting all five nido fragments inferred experimentally (see Fig. 1). The reduction of ortho-carborane is shown to initially produce 7,8, before rearranging to the experimental product, 7,9. meta-Carborane reduction proceeds to 7,9 directly, where the barrierless rearrangement process is rationalised by relation to the nido isomerisation pathways. In the completion of this work, we uncover and rationalise new dianionic 12-vertex carborane structures which we refer to as basket and inverted nido intermediates and characterise new, unexpectedly complex processes interconnecting nido species, ultimately linking all intermediates to the global minimum, 7,9.

Results

1. Formation of 1,7 and 4,7

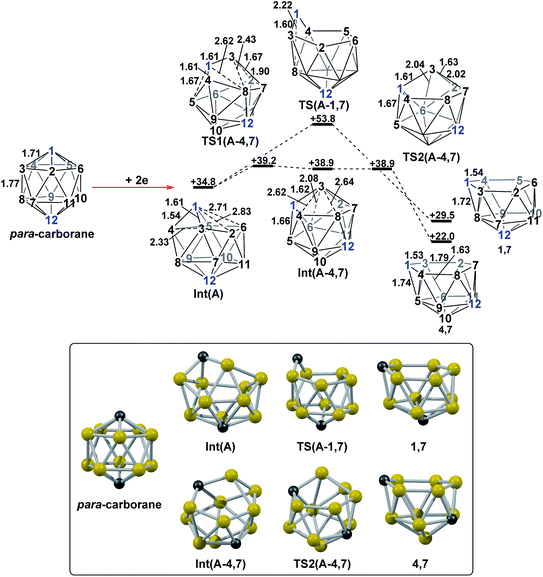
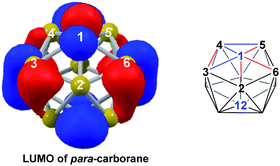
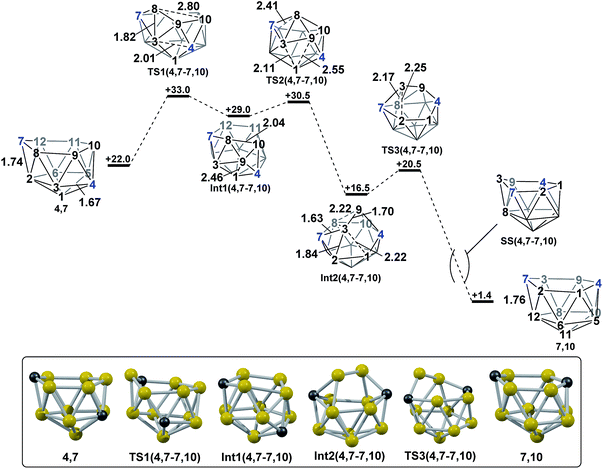
DFT calculations were performed at the BP86/6-31G** level using Gaussian 03 and we report zero-point corrected electronic energies, H, for all computed species relative to 7,9 (see Computational details). In order to model the reduction of para-carborane, first the neutral geometry was optimised, then two electrons were added and the system was re-optimised. This resulted in an initial reduced minimum, Int(A) (H = +34.8 kcal mol⁻¹; Fig. 2). Int(A) features 4-membered (B³–B⁸–B⁴–C¹) and 5-membered (B³–C¹–B⁵–B⁶–B²) open faces and is related to the nido geometry, 1,7, by a DSD process in the C¹–B³–B⁸–B⁴ face. This was characterised by decreasing the C¹⋯B⁸ distance, giving TS(A-1,7) (H = +53.8 kcal mol⁻¹). Through this process, C¹, which is 3-connected in Int(A), becomes 2-connected in the transition state and returns to 3-connected in 1,7, giving a barrier of 19.0 kcal mol⁻¹. Alternatively, movement of B³ across the 5-membered face towards B⁶ in Int(A) gives Int(A-4,7), through a lower barrier of 4.4 kcal mol⁻¹. Int(A-4,7) is topologically equivalent to Int(A) and features 4-membered C¹–B³–B²–B⁶ and 5-membered C¹–B³–B⁷–B⁸–B⁴ faces. We refer to such a topology as a basket intermediate (discussed in detail later) where here C¹ and B³ vertices bridge the remaining 10 vertices in a way that resembles a basket handle. From Int(A-4,7) decreasing the B³⋯B⁶ distance causes the 4-membered face to close viaTS2(A-4,7) (H = +38.9 kcal mol⁻¹) in what is effectively a barrierless process. Thereafter, a DSD process occurs in the C¹–B³–B⁶–B⁵ diamond, breaking the C¹–B⁶ connection and forming the B³–B⁵ connection, allowing C¹ to become 3-connected and furnishing the nido geometry, 4,7. These energy profiles suggest that processes decreasing the number of connections to carbon vertices and increasing the number of connections to boron vertices are favoured. The lower barrier to formation of 4,7 than of 1,7 also suggests that processes involving movement of boron are easier than those involving movement of carbon. This is supported by electronegativity arguments; the radial orbitals of the carbon vertices, being more contracted than those of boron, do not allow stabilisation of higher-connected sites or longer connections. The movement of vertices from the initial para-carborane geometry to give Int(A) can be rationalised by visualisation of the LUMO of para-carborane (Fig. 3). This features a π-antibonding interaction along the C¹–B⁶ connection and a further antibonding interaction between B³ and B⁴. Therefore the 2e occupation of this orbital is consistent with the breaking of these interactions to give a 4-membered C¹–B³–B⁸–B⁴ and a 5-membered C¹–B³–B²–B⁶–B⁵ face in Int(A).

Fig. 2 2e addition to para-carborane followed by isomerisation to the first nido intermediates, 1,7 and 4,7. Numbering of CH vertices (blue) and BH vertices (black) consistent with para-carborane. See inset for key computed structures along the pathways. Selected distances in Å and energies relative to 7,9 in kcal mol⁻¹. H atoms omitted for clarity.

Fig. 3 Left: representation of the LUMO of para-carborane at the BP86/6-31G** level; contour value = 0.05. Right: qualitative schematic shows bonding in blue and antibonding interactions in red. H atoms omitted for clarity.

2. Onward isomerisations of 1,7 and 4,7: general strategies

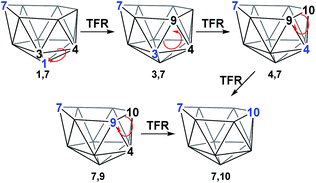
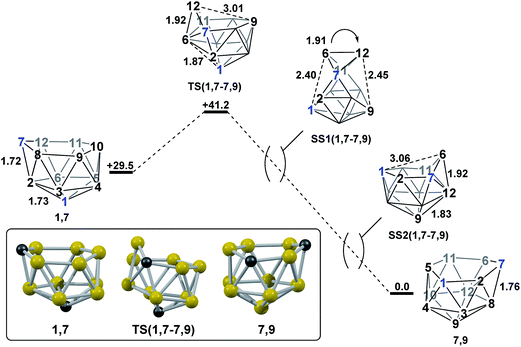
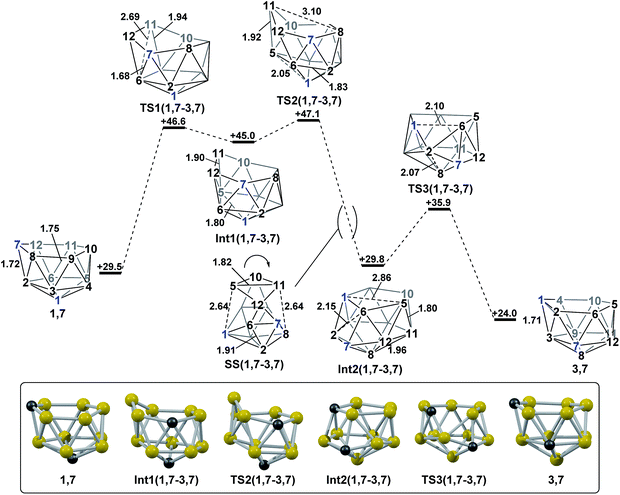
The geometries of 1,7 and 4,7 were considered as starting points towards formation of the remaining nido species, 3,7, 7,9 and 7,10. Initially, we considered the possibility of TFR processes linking nido isomers (Scheme 2); in 1,7, rotation of the C¹–B³–B⁴ triangle could be envisaged to interconvert 1,7 and 3,7 and rotation of the same triangle again, or C³–B⁹–B⁴, would exchange 3,7 and 4,7. Likewise, in 4,7, rotation of the C⁴–B⁹–B¹⁰ triangle could give 7,9 and 7,10. However, attempts to characterise such processes through potential energy surface searching (linear transits) were unsuccessful from either 1,7 or 4,7. Several atoms had to be fixed in position in order to prevent non-targetted rearrangement of the cluster. This suggested that the TFR process, though relevant to closo carborane isomerisation, was higher in energy than other processes available to the more flexible nido species. It was noted that the lowest energy vibrational mode of all nido species computed involves rotation of the 6-membered face above the 5-membered 2–3–4–5–6 belt, where the largest displacement is seen in the 7-position. Taking the lead from the mode-following approach of Wales,¹⁵ we used the transition state (TS) optimisation option in Gaussian 03,²⁵ which follows the lowest energy vibrational mode to a saddle-point on the PES, thus allowing low energy transition states to be sought a priori, direct from selected minima. The present C₂B₁₀H₁₂ clusters (which lack polyatomic exopolyhedral substituents) lend themselves to mode-following since the lowest energy vibrational mode always involves displacement of cluster vertices and so is productive towards cluster rearrangement. Mode-following was therefore always attempted in the first instance for any transition state search (see Computational Details). From 1,7 and 4,7 this revealed surprising and contrasting isomerisation processes, which see rearrangement of 1,7 to 7,9 in a single step and 4,7 to 7,10 in a multi-step process.

Scheme 2 TFR processes considered to interconvert nido geometries.

2.1 Formation of 7,9via isomerisation of 1,7. Mode-following from 1,7 provided a transition state, TS(1,7-7,9) (H = +41.2 kcal mol⁻¹; Fig. 4), connecting 1,7 directly to 7,9, through a barrier of just 11.7 kcal mol⁻¹. TS(1,7-7,9) is formed through a DSD process in the C⁷–B¹²–B⁶–B² diamond and exhibits a 3-connected boron vertex, B¹², which protrudes from the 6-membered open face by 0.81 Å w.r.t. the C⁷–B⁸–B⁹–B¹⁰–B¹¹ least-squares mean plane (for comparison, C⁷ protrudes by 0.28 Å and 0.27 Å from the open faces of 1,7 and 7,9 respectively). Visualisation of the single imaginary vibrational mode of TS(1,7-7,9) sees movement of B¹² relative to the open face, where the B¹²⋯B⁹ distance is 3.01 Å at the transition state geometry. Characterisation of TS(1,7-7,9)via IRC calculations revealed a remarkable and unanticipated process in which the cluster inverts in one step from 1,7, which has a CB₅ 6-membered open face, to 7,9, with a C₂B₄ open face. Fig. 4 shows the isomerisation process, with atom labelling consistent with the formal numbering of 1,7 to allow vertex movement to be followed; two snap-shots, SS1(1,7-7,9) and SS2(1,7-7,9), are shown to further aid in visualising the process and a movie is provided in the ESI.† The initial movement away from TS(1,7-7,9) involves pivoting about the long C⁷⋯B¹¹ diagonal of the C⁷–B⁶–B¹¹–B¹² diamond. SS1(1,7-7,9) illustrates the midpoint of this process. The pivoting continues, opening the C¹–B²–C⁷–B⁶–B¹¹–B⁵ face and closing the C⁷–B⁸–B⁹–B¹⁰–B¹¹–B¹² face of the starting structure. At SS2(1,7-7,9) the original open face has closed to give a geometry resembling a mirror image of TS(1,7-7,9), but with both C-vertices now on the open face. Finally, a barrierless DSD process in the C⁷–B⁶–B¹²–B⁸ diamond moves C⁷ into the 3-connected site to give 7,9.

Fig. 4 Isomerisation from 1,7 to 7,9. Numbering of CH vertices (blue) and BH vertices (black) consistent with 1,7. Inset shows the computed structure of TS(1,7-7,9). Selected distances in Å and energies relative to 7,9 in kcal mol⁻¹. H atoms omitted for clarity.

2.2 Formation of 7,10via isomerisation of 4,7. In contrast, the isomerisation of 4,7 to 7,10 was found to be a multistep process (Fig. 5) which was characterised through sequential mode-following steps. The first transition state, TS1(4,7-7,10) (H = +33.0 kcal mol⁻¹) again gives a low isomerisation barrier of 11.0 kcal mol⁻¹. TS1(4,7-7,10) is related to 4,7 by a single DSD process in the C⁷–B⁸–B³–B² diamond, resulting in a geometry topologically equivalent to TS(1,7-7,9), exhibiting a 3-connected B⁸ vertex protruding from the open face by 0.56 Å. Further distortion of the cluster has also occurred, where the B³–C⁴ connection has lengthened from 1.67 Å to 2.01 Å, producing an open B¹–B³–B⁹–C⁴ diamond. The imaginary mode associated with TS1(4,7-7,10) displays rotation of the B³–B⁸–B⁹ and C⁴–B⁹–B¹⁰ triangles, giving a hinging motion about the shared B⁹ vertex. Towards Int1(4,7-7,10) (H = +29.0 kcal mol⁻¹), this motion further elongates the B³–C⁴ connection to 2.57 Å, shortens the B⁹–B¹ distance to 2.46 Å and sees formation of an incipient B⁸–B¹⁰ connection of 2.04 Å, giving a 5-membered C⁷–B⁸–B¹⁰–B¹¹–B¹² face. Mode-following from Int1(4,7-7,10) gives TS2(4,7-7,10) (H = +30.5 kcal mol⁻¹) in which B⁸ has moved above the open face and the B⁸–B³ and B⁸–B⁹ connections are lengthened, but not broken, from 1.80 Å and 1.68 Å respectively in Int1(4,7-7,10) to 1.90 Å and 1.74 Å respectively in TS2(4,7-7,10). Similarly, the long B¹⋯B³ distance is lengthened further from 1.99 Å in Int1(4,7-7,10) to 2.11 Å in the transition state. From TS2(4,7-7,10) to Int2(4,7-7,10) the movement of B⁸ across the larger face is continued, leading to formation of connections B⁸–B¹² and B⁸–B¹¹ in Int2(4,7-7,10) while breaking the B³–B⁸ and B⁹–B⁸ connections. C₂ symmetric Int2(4,7-7,10) (H = +16.5 kcal mol⁻¹) is a further example of a basket intermediate with two equivalent 5-membered CB₄ faces, where the B³–B⁹ edge comprises the basket handle and the C vertices adopt bridgehead positions, 4 and 7. It is also relatively thermodynamically stable, having a lower energy than the starting nido species, 4,7. However, it is kinetically unstable due to the low barrier to its subsequent rearrangement. Rearrangement of Int2(4,7-7,10) to give a nido fragment is equivalent to that found for Int(A). Mode-following gives TS3(4,7-7,10) (H = +20.5 kcal mol⁻¹), in which the B³–B² connection is lengthened from 1.84 Å to 2.25 Å at the transition state and the B⁹–B⁸ connection shortens to 2.02 Å, giving a structure that closely resembles TS(A-1,7) and TS2(A-4,7). In visualising the IRC calculations from TS3(4,7-7,10) B³ is initially seen to remain 3-connected, however a DSD process in the B³–B⁸–B¹²–C⁷ diamond gives a 3-connected C⁷. Overall this transformation sees 4,7 rearrange to 7,10 where the former C⁴ vertex now adopts the C¹⁰ position and the B³–B⁸–B⁹ triangle is effectively transferred across the open face of the cluster in order for this to be accomplished. The process is exothermic with ΔH = −20.6 kcal mol⁻¹.

Fig. 5 Isomerisation from 4,7 to 7,10. Numbering of CH vertices (blue) and BH vertices (black) consistent with 4,7. Inset shows key computed structures along the pathway. Selected distances in Å and energies relative to 7,9 in kcal mol⁻¹. H atoms omitted for clarity.

2.3 Formation of 3,7via isomerisation of 1,7. The final remaining target nido fragment, 3,7, lies between 1,7 and 4,7 in energy (H = +24.0 kcal mol⁻¹, Fig. 6). It was therefore considered most likely to form in an exothermic process starting from 1,7. As the mode-following approach had previously defined the pathway from 1,7 to 7,9 (and not 3,7) we focussed on the reverse process, from 3,7 to 1,7. In this case, however, the lowest mode led to a facile, degenerate, two-step DSD process that links equivalent forms of 3,7 (ΔH^‡ = 6.2 kcal mol⁻¹; see ESI Fig. S1†). Instead a linear transit shortening the C¹ to B⁶ distance allowed us to locate a new minimum, Int2(1,7-3,7), that was comparable in energy to 1,7 and 3,7. Int2(1,7-3,7) is topologically equivalent to Int1(4,7-7,10). Therefore a process analogous to that linking 4,7 to Int1(4,7-7,10), where two triangle pivot about a shared vertex, was sought through STQN calculations. This resulted in location of TS3(1,7-3,7), through which the C¹–B³–B² and B²–B⁶–C⁷ triangles (as numbered in Fig. 6) pivot about B². The remaining challenge was then to connect Int2(1,7-3,7) to 1,7. Int2(1,7-3,7) features one 5-membered face including C¹. By analogy now with TS(1,7-7,9), it was envisaged that a process pivoting the B¹²–B⁵–B¹⁰–B¹¹ diamond about its long B¹²⋯B¹⁰ diagonal would provide the 1,7 geometry. Such a process, located by decreasing the C¹⋯B⁵ distance with the B⁵–B¹¹ distance frozen, gave TS2(1,7-3,7) (H = +47.1 kcal mol⁻¹). A snap-shot geometry, SS(1,7-3,7) is given in Fig. 6 to illustrate this process, where the B⁵–B¹⁰–B¹¹–B¹² diamond pivots about the long B¹⁰⋯B¹² diagonal. This gives (in the reverse direction) Int1(1,7-3,7) (H = +45.0 kcal mol⁻¹). Mode-following from Int1(1,7-3,7) gave TS1(1,7-3,7) directly, emphasising the ability of this technique to give the lowest energy transition state associated with a minimum, i.e. here locating the lower TS1(1,7-3,7) at ΔH = +1.6 kcal mol⁻¹ rather than the slightly higher TS2(1,7-3,7) at ΔH = +2.1 kcal mol⁻¹ w.r.t. Int1(1,7-3,7). The process linking 1,7 to Int1(1,7-3,7) involves a double-DSD step, where the first DSD (in the C⁷–B²–B⁶–B¹² diamond) has already occurred at TS1(1,7-3,7) and the second furnishes Int1(1,7-3,7). The overall isomerisation process forming 3,7 from 1,7 has a barrier of 17.6 kcal mol⁻¹, corresponding to TS2(1,7-3,7), and is exothermic by ΔH = −5.5 kcal mol.

Fig. 6 Isomerisation from 1,7 to 3,7. Numbering of CH vertices (blue) and BH vertices (black) consistent with 1,7. Inset shows key computed structures along the pathway. Selected distances in Å and energies relative to 7,9 in kcal mol⁻¹. H atoms omitted for clarity.

2.4 Remaining isomerisation pathway; 7,10 to 7,9. At this stage isomerisation processes have been characterised that rationalise the formation of all five nido species targeted. However, for completeness, it is desirable to connect all species to 7,9, the global minimum. 1,7 connects to 7,9 directly, whereas 3,7 connects to 7,9via1,7 and 4,7 connects to 7,9via7,10 (see Discussion section). The remaining isomerisation, from 7,10 to 7,9, is discussed below and shown in Fig. 7. Starting from 7,10, mode-following results in a degenerate process where the 3-connected C⁷ becomes 4-connected and B⁸ and B⁹ (or equivalent B¹² and B¹¹) become 3-connected. This is similar to the initial movement of vertices seen for the formation of 3,7 from 1,7, however here it does not lead to an isomerisation process. A linear transit was therefore adopted, increasing the C⁷–B² distance, to cause a DSD process in the C⁷–B⁸–B²–B¹² diamond. This gave TS1(7,10-7,9) (H = +27.7 kcal mol⁻¹) which leads to a basket intermediate, Int(7,10-7,9) (H = +2.8 kcal mol⁻¹), where C⁷–B¹¹ forms the basket handle. Int(7,10-7,9) is related to 7,9 through a DSD process in the C⁷–B¹¹–B⁶–B¹² diamond, which was characterised through location of TS2(7,10-7,9) (H = +21.4 kcal mol⁻¹). The isomerisation from 7,10 to 7,9 therefore involves two DSD processes, through a basket intermediate, with an overall barrier of 26.3 kcal mol⁻¹.

Fig. 7 Isomerisation from 7,10 to 7,9. Numbering of CH vertices (blue) and BH vertices (black) consistent with 7,9. Inset shows key computed structures along the pathway. Selected distances in Å and energies relative to 7,9 in kcal mol⁻¹. H atoms omitted for clarity.

3. Reductions of ortho- and meta-carborane

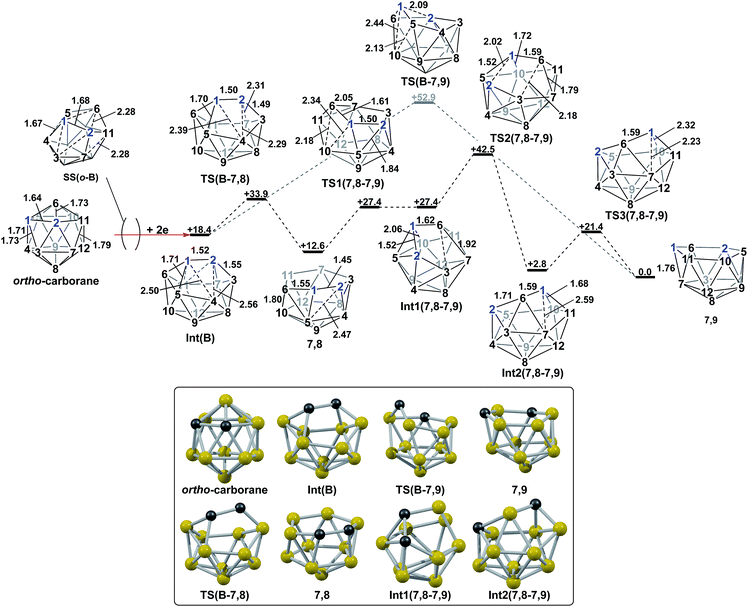
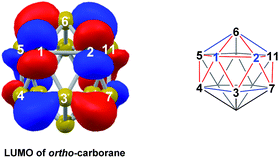
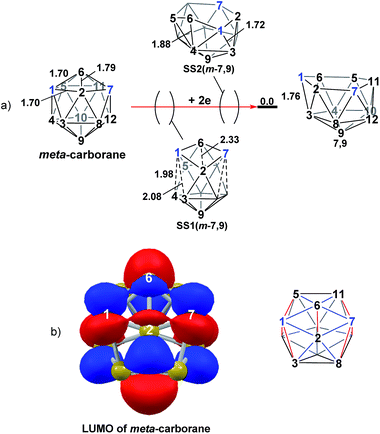
The experimental reductions of ortho- and meta-carborane each lead to 7,9.^2,5–7 Hermansson et al.²¹ showed in a study of carborane electron affinities that, at the HF level of theory, sequential addition of two electrons to meta-carborane produced a 7,9nido geometry, whereas ortho-carborane was only slightly distorted. Through the present DFT calculations, we have now characterised the rearrangement processes undergone by both of these species following 2e reduction, ultimately giving 7,9, which can be rationalised by relating them to the processes seen above. By analogy to the computational treatment of the reduction of para-carborane, 2e were added to the optimised geometry of ortho-carborane and the structure re-optimised as a dianion. This gave Int(B) (H = +18.4 kcal mol⁻¹ above 7,9; Fig. 8). Int(B) is another example of a basket intermediate, where here the geometry is C₂ symmetric and the C¹ and C² vertices form the basket handle. The C¹–C² connection in Int(B) is shortened to 1.52 Å w.r.t. 1.64 Å in ortho-carborane, indicative of single bond character. From Int(B), a basket collapse process was characterised through TS(B-7,9) (H = +52.9 kcal mol⁻¹; see Fig. 8, grey pathway) and involves DSD processes in the C¹–B⁵–B¹⁰–B⁶ diamond (with C¹⋯B¹⁰ and B⁵⋯B⁶ distances of 2.44 Å and 2.58 Å respectively) and breaking of the C¹–C² connection to give 7,9 in a single step. However, this process exhibits a high overall barrier of 34.5 kcal mol⁻¹, consistent with it being dominated by the breaking of a C–C connection with single bond character. An alternative basket collapse process was characterised through mode-following (Fig. 8, black pathway). This pathway initially maintains the C¹–C² connection, giving 7,8 through a low barrier of 15.5 kcal mol⁻¹ in which the C¹–C² connection is shortened still further to 1.45 Å. Mode-following from 7,8 led to a degenerate rearrangement involving a DSD process in the C¹–C²–B⁴–B⁵ diamond (as numbered in Fig. 8), forming a C²–B⁵ connection through a barrier of 14.8 kcal mol⁻¹. Linear transits were therefore conducted to discover a pathway leading to 7,9. A low energy transition state, TS1(7,8-7,9) (H = +27.4 kcal mol⁻¹) was located, and provided a basket intermediate, Int1(7,8-7,9). From here, C¹–C² bond breaking proceeds through TS2(7,8-7,9) at over 10 kcal mol⁻¹ lower than TS(B-7,9) (H = +42.5 kcal mol⁻¹), giving a barrier of 29.9 kcal mol⁻¹ from 7,8. This process leads to Int2(7,8-7,9) at H = +2.8 kcal mol⁻¹, which is identical to Int(7,10-7,9). Therefore the basket collapse process described above to give 7,9 is repeated in this pathway; here forming the C¹–B⁷ connection through a DSD process in the C¹–B¹¹–B⁷–B⁶ diamond of the Int2(7,8-7,9)basket. The nido-7,8 isomer is implicated experimentally in the synthesis if 4,1,2-MC₂B₁₀ species from ortho-carborane, where exopolyhedral hydrocarbyl or silyl tethers connecting the C-vertices ensure the C positions remain adjacent.^3,26,27 With the removable silyl tether metallation with M = {CoCp} leads to the concurrent formation of the expected 4,1,2-MC₂B₁₀ species, but also the 4,1,6-MC₂B₁₀ isomer, indicating that isomerisation of the nido-7,8 fragment to the 7,9 form is possible.²³ The initial strengthening of the C¹–C² connection in Int(B)cf. ortho-carborane contrasts with the 2e addition to 1,2-Ph₂-1,2-closo-C₂B₁₀H₁₀ (towards [7,9-Ph₂-7,9-nido-C₂B₁₀H₁₀]²⁻), where the C¹–C² connection breaks due to a σ-C–C antibonding component in the LUMO orbital of the neutral species.²⁴ In the LUMO of ortho-carborane (Fig. 9a) a π-antibonding interaction is seen between the C vertices, suggesting the connection would indeed be lengthened on occupation of the orbital. Further antibonding interactions are seen between C² and the B³–B⁷ edge and those equivalent by C_2v symmetry (C¹–{B³–B⁴}, C¹–{B⁵–B⁶} and C²–{B⁶–B¹¹}) and along the B⁴–B⁵ (and B⁷–B¹¹) connections. Upon visualising the optimisation an initial lengthening of connections with antibonding interactions was noted (see ESI† for Movie). A snapshot of this (Fig. 8, SS(o-B)) shows the C¹–C² connection initially lengthens from 1.64 Å in ortho-carborane to ca. 1.7 Å. In addition, the distances from the C vertices to B³ and B⁶ and the B⁴–B⁵ and B⁷–B¹¹ connections are also lengthened at SS(o-B). As the optimisation continues the C_2v symmetry is reduced to C₂ by reformation of the C²–B³ (1.55 Å), C¹–B⁵ (1.71 Å) and C¹–C² (1.52 Å) connections in Int(B).

Fig. 8 2e addition to ortho-carborane followed by isomerisation to 7,9 through a one-step pathway (grey) or a multi-step pathway, via7,8 (black). Numbering of CH vertices (blue) and BH vertices (black) consistent with ortho-carborane. Inset shows key computed structures along the pathway. Selected distances in Å and energies relative to 7,9 in kcal mol⁻¹. H atoms omitted for clarity.

Fig. 9 Left: LUMO of ortho-carborane at the BP86/6-31G** level; contour value = 0.05. Right: qualitative schematics show key bonding (blue) and antibonding (red) interactions. H atoms omitted for clarity.

Addition of 2e to meta-carborane led directly to the location of 7,9 (Fig. 10a) (see ESI† for movie). During the optimisation the structure initially distorts with retention of C_2v symmetry, consistent with the population of the LUMO of meta-carborane (Fig. 10b and see snap-shot geometry SS1(m-7,9) in Fig. 10a). Subsequently, B⁶–C⁷ lengthens and the symmetry is lost. At SS2(m-7,9), a B⁶–B⁴ connection is formed and the connections from C⁷ to B⁸, B¹¹ and B¹² have reformed. SS2(m-7,9) is equivalent to SS2(1,7-7,9) (Fig. 4) and indeed undergoes a related DSD process, here in the B³–B⁴–B⁶–C¹ diamond to give 7,9.

Fig. 10 (a) 2e addition to meta-carborane giving 7,9. Numbering of CH vertices (blue) and BH vertices (black) consistent with meta-carborane with selected distances in Å. (b) Left: representation of the LUMO orbital of meta-carborane at the BP86/6-31G** level; contour value = 0.05. Right: qualitative schematic shows bonding in blue and antibonding interactions in red. H atoms omitted for clarity.

Discussion

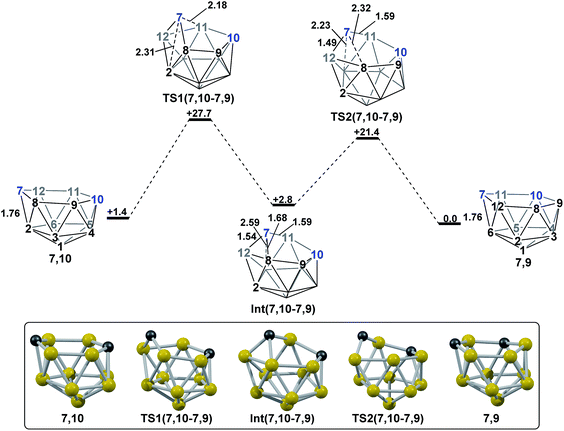
Polyhedral expansion of closo-C₂B₁₀ carboranes with metal fragments produces a range of MC₂B₁₀ species which imply the intermediacy of 1,7-, 3,7-, 4,7-, 7,9- and 7,10-isomers of the nido-[C₂B₁₀]²⁻ species. Here we have used DFT calculations to characterise the isomerisation pathways that link these various nido isomers. Our study has revealed several unusual new intermediates and their unforeseen rearrangement pathways which are categorised and rationalised below.

Following the addition of two electrons to the optimised geometry of para-carborane, 1,7 and 4,7 are formed as the initial nido species (Scheme 3). Thereafter, 1,7 connects to 7,9, through a single transition state, with a barrier of 11.7 kcal mol⁻¹. In contrast, the isomerisation of 4,7 proceeds through a facile multi-step process to form 7,10, but with a similar overall barrier of 11.0 kcal mol⁻¹. The remaining nido species, 3,7, is formed in an alternative 3-step process from 1,7 with a barrier of 17.6 kcal mol⁻¹. In order to connect all nido species to the global minimum, 7,9, additional pathways were sought from 7,10, 3,7 and 4,7. From 7,10, a two-step process was characterised with a barrier of 26.3 kcal mol⁻¹. From 3,7, while a single step process was characterised for isomerisation to 7,9 with a barrier of 28.5 kcal mol⁻¹ (see ESI Fig. S2†) this is higher than the reverse process from 3,7 to 1,7 (above; ΔH^‡ = 23.1 kcal mol⁻¹) and therefore 3,7 likely isomerises to 7,9via 1,7. Similarly, a direct pathway from 4,7 to 7,9 was not found and so formation of 7,9 from 4,7 is thought to proceed through 7,10 (ΔH^‡ = 11.0 kcal mol⁻¹). An additional nido species, 7,8, was found to be formed following 2e addition to ortho-carborane and isomerises to 7,9 through a barrier of 29.9 kcal mol⁻¹. 2e reduction of meta-carborane leads directly to 7,9. Degenerate pathways, where the start and end points of a rearrangement are the same nido species, were characterised for 7,9 (ΔH^‡ = 10.7 kcal mol⁻¹), 7,10 (ΔH^‡ = 11.1 kcal mol⁻¹), two examples for 3,7 (ΔH^‡ = 6.2 kcal mol⁻¹ and 20.8 kcal mol⁻¹) and 7,8 (ΔH^‡ = 14.8 kcal mol⁻¹).

Scheme 3 Interconnection of 12-vertex nido carborane dianions and their relation to 12-vertex closo carboranes. Relative energies of nido species and the barriers associated with rearrangement processes (denoted ^‡) given in kcal mol⁻¹.

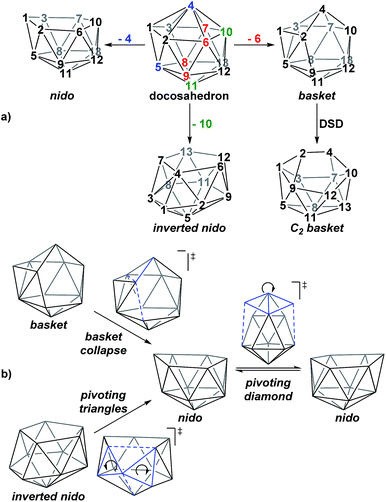
A family of basket intermediates, which are often energetically comparable to conventional nido fragments, were located along several of the characterised pathways. In a basket intermediate, two vertices form a basket handle bridging the remaining 10 vertices, with examples located in this study including Int(A), Int(A-4,7), Int(7,10-7,9), Int1(7,8-7,9) and Int2(7,8-7,9) (all with C₁ symmetry) and Int2(4,7-7,10) and Int(B) (with C₂ symmetry with the CH vertices in the bridgehead positions and basket handle positions respectively). As shown in Scheme 4a, starting from the docosahedron, a C₁-basket may be produced through removal of one of the 5-connected vertices 6–9 (red), with lengthening of the 1–4 distance to produce the requisite 4- and 5-membered faces. The C₂-basket intermediates are related to the relevant C₁-basket by a DSD in the 1–2–5–9 diamond and lengthening of the 3–4 distance. Two additional key intermediates, Int1(4,7-7,10) and Int2(1,7-3,7), we refer to as inverted nido geometries, due to the 6-membered belt of vertices, rather than the 5-membered belt, being capped by a single vertex. The inverted nido motif is derived from the docosahedron by removal of a 5-connected vertex (10 or 11, green). A classical nido geometry is produced through removal of a 6-connected vertex (4 or 5, blue).²⁸ In order to test the validity of this empirical observation, the idealised [B₁₃H₁₃]²⁻ docosahedron was computed, the appropriate vertices removed and the structure re-optimised as [B₁₂H₁₂]⁴⁻ fragments. The nido and inverted nido were located as minima (H = 0.0 and +25.8 respectively; see ESI†). The basket geometry was found to collapse to a nido structure, suggesting the C vertices are required to stabilise the distorted geometry, however, the C₂basket was located as a transition state that exchanges equivalent nido structures (H = +18.6 kcal mol⁻¹; see ESI†).

Scheme 4 (a) Relationship between the docosahedron and nido, basket and inverted nido geometries with numbering consistent with the docosahedron. (b) Processes characterised that interconvert these geometries.

The structural types discussed above tend to access specific rearrangement processes. From nido species, the initial step in the isomerisation is most often to move the 3-connected C⁷ vertex into a 4-connected position. This then triggers movement of the neighbouring vertices resulting in net rotation of the 6-membered belt of vertices above the 5-membered belt. Such processes are also responsible for the degenerate exchanges characterised in 7,8, 7,9 and 7,10. Three additional processes are found (Scheme 4b): a common DSD process by which basket intermediates undergo basket collapse to give nido species (Scheme 4b, upper left); the pivoting of a 4-vertex diamond about its long diagonal to directly exchange nido geometries (Scheme 4b, right; seen in the isomerisations from 1,7 to 7,9, from 1,7 to 3,7 and in the higher energy degenerate process at 3,7 (see ESI, Fig. S1†)) and the pivoting of two triangles about a shared vertex exchanging inverted nido and nido geometries (Scheme 4b lower left; seen in the isomerisations of 4,7 to 7,10 and 1,7 to 3,7).

Conclusions

The rearrangements of dianionic 12-vertex nido-carboranes, [C₂B₁₀H₁₂]²⁻, have been characterised through DFT calculations. para-Carborane rearranges to 1,7 and 4,7 as the first nido species, where experimentally, 1,7, 3,7, 4,7, 7,9 and 7,10 are produced. Isomerisation processes have been characterised connecting 1,7 to 7,9, 4,7 to 7,10, 1,7 to 3,7 and 7,10 to 7,9, thus rationalising the experimental formation of these species and showing how they are interconnected. Reduction of ortho-carborane gives 7,8 as the first nido species which subsequently isomerises to the expected 7,9, while meta-carborane rearranges directly to 7,9. The initial movements of vertices away from closo geometries, following the addition of two electrons, is related to the LUMO of the neutral species.

In the characterisation of these isomerisation processes, where possible through a priori mode-following calculations, a series of common intermediate topologies as well as the unexpectedly complex processes by which they interconnect have been uncovered and rationalised. Basket intermediates (e.g.Int(A), Int(A-4,7), Int2(4,7-7,10), Int(7,10-7,9) and Int(B)) are characterised by a two-vertex basket handle bridging the remaining 10 vertices; inverted nido intermediates (Int1(4,7-7,10) and Int2(1,7-3,7)) exhibit a 5-membered belt and a 6-membered belt capped by the remaining vertex. The geometries of these new intermediates, like nido species themselves, are related to the 13-vertex docosahedron by removal of a single vertex. The pathways through which carborane dianions isomerise, driven by the thermodynamic preference for low-connected C vertices, are most often initiated by movement of the 3-connected C⁷ vertex, common to all nido species, into a 4-connected position through a DSD step, forcing a B vertex into a destabilised 3-connected site and leading to rearrangement of the cluster. Isomerisation continues through processes such as the pivoting of a 4-vertex diamond about its long diagonal. This can directly lead to a nido geometry or produce a basket or inverted nido intermediate. Basket intermediates can undergo a basket collapse process, characterised by DSD steps, giving rise to a nido geometry, while inverted nido intermediates convert to nido geometries through the pivoting of two 3-vertex triangles about a shared vertex.

Computational details

Calculations were performed using Gaussian 03, Revision D.01 employing the BP86 functional^29,30 and 6-31G** basis sets³¹ for B, C and H atoms. Zero-point corrected energies, H, are reported in kcal mol⁻¹ relative to 7,9. Analytical frequency calculations were used to confirm geometries as minima (all positive eigenvalues) or transition states (one negative eigenvalue). Transition states were further characterised through IRC calculations.^32,33 Mode-following calculations used the ‘OPT = TS’ option in Gaussian along with the GDIIS algorithm, where convergence constraints were set to ‘verytight’ in order to force the optimisation to move away from a formally minimum energy starting geometry, itself optimised with default convergence constraints. Synchronous Transit-Guided Quasi-Newton (STQN) calculations were run with the ‘QST2’ option (two intermediate geometries given as input) and the structure generated used as input in a transition state optimisation.

Acknowledgements

We thank the EPSRC for support (DMcK funded by project EP/E02971X/1).

Notes and references

1. K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1.
2. G. B. Dunks, M. M. McKown and M. F. Hawthorne, J. Am. Chem. Soc., 1971, 93, 2541.
3. A. Burke, D. Ellis, B. T. Giles, B. E. Hodson, S. A. Macgregor, G. M. Rosair and A. J. Welch, Angew. Chem., Int. Ed., 2003, 42, 225.
4. S. Zlatogorsky, M. J. Edie, D. Ellis, S. Erhardt, M. E. Lopez, S. A. Macgregor, G. M. Rosair and A. J. Welch, Angew. Chem., Int. Ed., 2007, 46, 6706.
5. M. R. Churchill and B. G. DeBoer, J. Chem. Soc., Chem. Commun., 1972, 1326.
6. G. B. Dunks, R. J. Wiersema and M. F. Hawthorne, J. Am. Chem. Soc., 1973, 95, 3174.
7. T. D. Getman, C. B. Knobler and M. F. Hawthorne, Inorg. Chem., 1990, 29, 158.
8. D. Grafstein and J. Dvorak, Inorg. Chem., 1963, 2, 1128.
9. S. Papetti and T. L. Heying, J. Am. Chem. Soc., 1964, 86, 2295.
10. V. I. Stanko, V. A. Brattsev and Y. V. Gol'tyapin, Zh. Obshch. Khim., 1969, 39, 2686.
11. C. A. Brown and M. L. McKee, J. Mol. Model., 2006, 12, 653.
12. B. W. Hutton, F. MacIntosh, D. Ellis, F. Herisse, S. A. Macgregor, D. McKay, V. Petrie-Armstrong, G. M. Rosair, D. S. Perekalin, H. Tricas and A. J. Welch, Chem. Commun., 2008, 5345.
13. W. N. Lipscomb, Science, 1966, 153, 373.
14. I. J. Sugden, D. F. Plant and R. G. Bell, Chem. Commun., 2013, 49, 975.
15. D. J. Wales, J. Am. Chem. Soc., 1993, 115, 1557.
16. L. I. Zakharkin and V. N. Kalinin, Dokl. Akad. Nauk SSSR, 1966, 169, 590.
17. S. Robertson, D. Ellis, G. M. Rosair and A. J. Welch, Appl. Organomet. Chem., 2003, 17, 518.
18. S. Robertson, D. Ellis, G. M. Rosair and A. J. Welch, J. Organomet. Chem., 2003, 680, 286.
19. S. Robertson, R. M. Garrioch, D. Ellis, T. D. McGrath, B. E. Hodson, G. M. Rosair and A. J. Welch, Inorg. Chim. Acta, 2005, 358, 1485.
20. M. L. McKee, M. Buehl and P. v. R. Schleyer, Inorg. Chem., 1993, 32, 1712.
21. K. Hermansson, M. Wójcik and S. Sjöberg, Inorg. Chem., 1999, 38, 6039.
22. D. Ellis, D. McKay, S. A. Macgregor, G. M. Rosair and A. J. Welch, Angew. Chem., Int. Ed., 2010, 49, 4943.
23. A. McAnaw, M. Elena Lopez, G. Scott, D. Ellis, D. McKay, G. M. Rosair and A. J. Welch, Dalton Trans., 2012, 10957.
24. H. Tricas, M. Colon, D. Ellis, S. A. Macgregor, D. McKay, G. M. Rosair, A. J. Welch, I. V. Glukhov, F. Rossi, F. Laschi and P. Zanello, Dalton Trans., 2011, 40, 4200.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision D.01, Gaussian Inc., Wallingford, CT, USA, 2004.
26. R. McIntosh, D. Ellis, J. Gil-Lostes, K. J. Dalby, G. M. Rosair and A. J. Welch, Dalton Trans., 2005, 1842.
27. J. Zhang, L. Deng, H.-S. Chan and Z. Xie, J. Am. Chem. Soc., 2007, 129, 18.
28. M. A. Fox and K. Wade, Pure Appl. Chem., 2003, 75, 1315.
29. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
30. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
31. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213.
32. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
33. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.

---

Footnotes

† Electronic supplementary information (ESI) available: Movies of the 1,7 to 7,9 isomerisation (17-79_isom.avi), ortho-carborane reduction (ortho-carborane_RED.avi) and meta-carborane reduction (meta-carborane_RED.avi); alternative reaction profiles; computed Cartesian coordinates and energies for all structures. See DOI: 10.1039/c5sc00726g

‡ Present address: School of Chemistry, St Andrews University, North Haugh, St Andrews, Fife, KY16 9ST, UK.

---