Open Access Article
Open Access ArticleTurning it off! Disfavouring hydrogen evolution to enhance selectivity for CO production during homogeneous CO2 reduction by cobalt–terpyridine complexes†
Noémie
Elgrishi
,
Matthew B.
Chambers
and
Marc
Fontecave
*
Laboratoire de Chimie des Processus Biologiques, UMR 8229 CNRS, UPMC Univ Paris 06, Collège de France, 11 Place Marcelin Berthelot, 75231 Paris Cedex 05, France. E-mail: marc.fontecave@college-de-france.fr; Fax: +33 1 44271356; Tel: +33 1 44271360
First published on 18th February 2015
Abstract
Understanding the activity and selectivity of molecular catalysts for CO2 reduction to fuels is an important scientific endeavour in addressing the growing global energy demand. Cobalt–terpyridine compounds have been shown to be catalysts for CO2 reduction to CO while simultaneously producing H2 from the requisite proton source. To investigate the parameters governing the competition for H+ reduction versus CO2 reduction, the cobalt bisterpyridine class of compounds is first evaluated as H+ reduction catalysts. We report that electronic tuning of the ancillary ligand sphere can result in a wide range of second-order rate constants for H+ reduction. When this class of compounds is next submitted to CO2 reduction conditions, a trend is found in which the less active catalysts for H+ reduction are the more selective towards CO2 reduction to CO. This represents the first report of the selectivity of a molecular system for CO2 reduction being controlled through turning off one of the competing reactions. The activities of the series of catalysts are evaluated through foot-of-the-wave analysis and a catalytic Tafel plot is provided.
Introduction
The reduction of carbon dioxide (CO2) is a promising strategy by which to store renewable energy in various fuels with high gravimetric and volumetric densities while also conforming to current infrastructures within most developed societies.1–3 However, catalysts for CO2 reduction are often plagued by lack of selectivity due to the numerous possible CO2 reduction carbon-containing products, as well as the constant competition with proton reduction to H2. The lack of selectivity would subsequently require additional purification and isolation processes in order to obtain the particular product of interest, resulting in increased total system costs. Among various classes of catalysts, molecular ones offer the possibility to synthetically finely tune their structure and reactivity and allow for a deeper understanding of underlying mechanistic pathways, thus paving the way to the rational design of more selective catalysts.4–6 This molecular approach has been favoured recently, with a shift to the study of first row transition metals combined with simple cheap ligands.7–13 However, while most studies have been dealing mainly with catalytic efficiency using empirically selective catalysts,14,15 through comparison of a variety of metal–ligand combinations, rational optimization of the selectivity for a particular product has been generally unexplored in molecular CO2 reduction catalytic systems.We have recently revisited the CO2 reduction chemistry of metal–terpyridine catalytic systems, and reported that the cobalt (Co–tpy) and nickel based catalysts can reduce CO2 to CO and that in the case of cobalt a mixture of H2 and CO is produced.16 The proportions of H2 produced were shown to be easily tuneable through the modulation of the applied potential during bulk electrolysis, motivating our desire to understand the parameters allowing this tuneability. To this end, we sought to investigate the possibility of enhancing selectivity for CO production through the rational inhibition of the hydrogen evolution reaction (HER), with a goal of enhancing the faradic yields observed for CO2 reduction to CO. While seemingly backwards at first, the strategy of suppressing the H2 evolution reaction in order to increase faradic efficiencies for a more chemically challenging reduction has recently been proposed in the course of the study of CO reduction on oxide-derived nanocrystalline copper electrodes in water, but has yet to be extended to molecular-based catalytic systems.17
It is practically challenging to study and optimize CO2 reduction independent of concomitant proton reduction as CO2 reduction typically involves a proton source. Thus in an attempt to better understand the underlying chemical principle leading to the controlled production of a CO/H2 ratio of products, we decided to focus first on understanding the hydrogen evolution reaction as catalysed by Co–tpy, independently of CO2 reduction. To this end, the proton reduction reaction was studied independently as the foot-of-the-wave analysis (FOWA) was performed on Co–tpy as well as on cobalt systems bearing substituted terpyridine ligands (Co–tpyY2X) to allow for tuning of the electronics of the complex. These simple ligand modifications (Scheme 1) are shown to have an impact on the rate constant for H2 evolution from acetic acid in DMF.
Polypyridine cobalt complexes have recently received renewed interest as electrocatalysts for proton reduction.18–20 Here we report for the first time the activity for proton reduction by cobalt terpyridine-based homogeneous systems. We next observed the influence of these modifications on the electro-assisted catalytic reduction of CO2 to CO, focusing on the influence that tuning the electronics of the ligand has on turning off H2 evolution during CO2 reduction to CO. Our findings help understanding the selectivity trends observed, and should allow for future rational ligand modifications to obtain next generation catalysts.
Results and discussion
Cobalt–terpyridine complexes as catalysts for hydrogen evolution
Precedent is scarce for mononuclear cobalt–terpyridine systems catalysing the HER. To our knowledge the only two previous reports of such systems consist of H2 evolution from [Co(tpy)2]2+ embedded in a Nafion® membrane in water21 and a recent report on a Co(tpy)(phen) catalyst grafted on an electrode for H2 evolution from water.22 To study the HER independently from CO2 reduction, in organic media, proton reduction by a class of five different cobalt terpyridine complexes was studied in DMF with acetic acid as the proton source. Acetic acid was chosen as the proton source for its relatively low pKa in organic media (13.5 in DMF), and for its highly negative reduction potential on a bare glassy carbon electrode in organic solvents,23 allowing for the study of Co–tpyY2X on glassy carbon by CV to be virtually unaffected by background H+ reduction at the electrode. Since it is known that variable amounts of water affect the HER on glassy carbon electrode in organic solvent in the presence of acetic acid, a strictly anhydrous DMF solvent was chosen for this study.23,24The structure of the compounds studied is presented in Scheme 1. Compounds 1–5 comprise of a cobalt(II) centre coordinated to two substituted terpyridine ligands. The modifications of the electronic structure occur through substituent groups placed para to the nitrogen atoms so as to minimize perturbation of the steric properties of the compounds around the cobalt atom.
Under an inert atmosphere of argon in anhydrous DMF, compounds 1–5 exhibited the CVs at 50 mV s−1 scan rate presented in Fig. 1. In the interrogated potential range, all of the compounds exhibited two reversible, diffusion-controlled one-electron waves. The first feature is attributed to a CoII/I metal-based reduction, ranging from −1.14 for 1 to −1.34 V vs. Fc+/Fc for 4, and the second feature is assigned to a ligand-based reduction, ranging from −1.92 for 1 to −2.17 V vs. Fc+/Fc for 5. If the parent compound with unsubstituted terpyridine ligands, 3, is taken as a reference point for comparison, as expected, the ligand-based reductions are found at more positive potentials for complexes with more electron-withdrawing substitutions on the terpyridine, (1vs.3). Conversely, the more electron-donating substituent give rise to more negative ligand-based reductions (4 and 5vs.3). The presence of a phenyl ring allowing for electron delocalization explains the relative reduction potentials of 2vs.3. In the case of the metal-based reduction, the redox potentials follow a behaviour consistent with the trend in Hammett parameter of the substituent noted “X” in Scheme 1, indicating that the electronic density on the metal is dictated more strongly by the substituent on the para position of the central pyridine ring in [Co(tpyY2X)2]2+(ESI Fig. S1†).
 | ||
Fig. 1 Cyclic voltammograms under Ar at 50 mV s−1 of 1 mM solutions of compounds 1 ( blue), 2 ( blue), 2 ( green), 3 ( green), 3 ( orange), 4 ( orange), 4 ( red) and 5 ( red) and 5 ( brown) in DMF, TBAPF6 0.1 M, on a glassy carbon electrode. brown) in DMF, TBAPF6 0.1 M, on a glassy carbon electrode. | ||
When treated with increasing amounts of acetic acid, compounds 1–5 exhibit the voltammograms presented in Fig. 2. Contrary to the metal-based reduction where minimal effect is found, the ligand-based reduction showed an enhancement of the cathodic current accompanied by a loss of reversibility, with the cathodic current increasing with the increase of acetic acid concentration. Electron-deficient compound 1 was observed to have the least current enhancement upon treatment with acetic acid whereas 4 and 5 appeared to be the most active. A clear trend was observed in which more cathodic current enhancement was found with cobalt complexes of more electron-donating terpyridine ligands. As the scan rate is increased (50, 100, 250, 500, 750 and 1000 mV s−1) the behaviour persists, with the catalytic current showing very little dependence on scan rate. This behaviour is attributed to catalytic proton reduction, as confirmed by the bulk electrolysis of 3 under similar conditions yielding H2 as the only product in over 80% faradic yield (see ESI Fig. S2†). Thus, as expected, enhancing the nucleophilicity of the Co complex by ligand modification results in redox couples at more negative potentials and in a greater overpotential being required for proton reduction while at the same time favouring protonation, thus enhancing the catalytic activity for hydrogen formation.
On the nature of the active species: mono- or bis-terpyridine?
The initial complex under consideration is [Co(tpy)2](PF6)2 with a full coordination sphere, theoretically unsuitable for substrate binding and activation. Indeed, although there exists one report of a relevant pyridine-coordinated cobalt complex with a coordination number greater than 6, cobalt complexes of such high coordination numbers remain exceedingly rare.25 Therefore, to generate an open coordination site through which catalysis can proceed, two options exist: (a) de-coordination and rotation of either one or two peripheral pyridine rings or (b) loss of an entire terpyridine ligand. Whereas both processes have been speculatively included within catalytic cycles, we favour catalysis occurring through an active species comprising of only one terpyridine ligand due to precedent for a similar structure in an analogous system.26The ability of [Co(tpy)2]2+ to liberate a tpy ligand, in a reaction depicted in eqn (1), has been studied previously and has been shown to have a strong dependence on the nature of the solvent.27,28
 | (1) |
The rate constant for reaction (1) has been measured recently in different solvents, and was shown to be kd = 3.2 10−2 s−1 in conditions similar to those utilized for catalysis within this report (DMF as the solvent).29 Upon reduction of CoII to CoI, the ability should increase and the loss of a tpy ligand become easier. Although the bisterpyridine complex is clearly favoured (we have confirmation that pure synthetic Co(tpy)Cl2 loses its green colour as soon as it is dissolved in a solvent such as DMF and disproportionates – eqn (2)), this precedent clearly suggests the kinetic viability of a monoterpyridine complex, especially upon further reduction.
 | (2) |
In an attempt to glean insights into the redox potential of a possible Co–monotpy species in DMF and identify possible electrochemical features, the evolution of the CV features of various proportions of cobalt dichloride and terpyridine were analysed in order to manipulate the equilibrium presented in eqn (2).
CVs of a 2 mM solution of terpyridine in DMF under argon were initially collected. No signal is observed in the potential range scanned (Fig. 3, black). CoCl2 was then added to this solution to obtain a solution of 2 mM terpyridine with 1 mM of CoCl2 (Fig. 3, blue). Under these conditions, similar to those of our catalytic assays, the cyclic voltammograms were found to be identical to those collected with pre-synthesized Co(tpy)2. Subsequently, additional CoCl2 was added to the electrochemical cell in order to shift the equilibrium depicted in eqn (2) towards a possible Co–monotpy complex.
A new electrochemical feature could be observed at −1.40 V vs. Fc+/Fc when a ratio of CoCl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tpy of 2
tpy of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 was obtained (Fig. 3, green). We have assigned the new electrochemical feature found at −1.40 V vs. Fc+/Fc as the CoII/I couple associated with a Co–monotpy given that it can neither be attributed to Co(tpy)2, CoCl2 nor tpy itself (ESI Fig. S3†). Upon further addition of CoCl2, the new electrochemical feature was observed to increase in intensity while the [Co(tpy)2]2+/[Co(tpy)2]+ feature decreased in intensity.
2 was obtained (Fig. 3, green). We have assigned the new electrochemical feature found at −1.40 V vs. Fc+/Fc as the CoII/I couple associated with a Co–monotpy given that it can neither be attributed to Co(tpy)2, CoCl2 nor tpy itself (ESI Fig. S3†). Upon further addition of CoCl2, the new electrochemical feature was observed to increase in intensity while the [Co(tpy)2]2+/[Co(tpy)2]+ feature decreased in intensity.
Under conditions of the greatest excess of CoCl2 relative to terpyridine tested (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), the small feature assigned to Co(tpy)2 was still present in the mixture, as seen by the presence of the anodic feature of the [Co(tpy)2]2+/[Co(tpy)2]+ couple. This further shows that the preferred state is Co–bistpy, and is consistent with our observation that Co(tpy)2 is the only observable species in the bulk during catalysis under similar conditions.16
2), the small feature assigned to Co(tpy)2 was still present in the mixture, as seen by the presence of the anodic feature of the [Co(tpy)2]2+/[Co(tpy)2]+ couple. This further shows that the preferred state is Co–bistpy, and is consistent with our observation that Co(tpy)2 is the only observable species in the bulk during catalysis under similar conditions.16
A similar experiment was conducted under catalytic conditions, where the height of the catalytic peak was monitored as different ratios of tpy and CoCl2 were added (ESI Fig. S4†). A catalytic peak was observed even in proportions of Co/tpy of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This alone does not discriminate between an active species of 2 or 1 tpy per cobalt since as noted above, 1
1. This alone does not discriminate between an active species of 2 or 1 tpy per cobalt since as noted above, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of Co and tpy will disproportionate to form a part of Co(tpy)2. However, when a second equivalent of terpyridine was added, the catalytic current decreased by 15% (ESI Fig. S4†). Should Co(tpy)2 be the active catalyst, the addition of the 2nd equivalent of tpy would be expected to increase the catalytic current observed. Since the reverse is observed, this experiment supports the idea of an active catalyst containing less than 2 tpy per cobalt centre.
1 mixtures of Co and tpy will disproportionate to form a part of Co(tpy)2. However, when a second equivalent of terpyridine was added, the catalytic current decreased by 15% (ESI Fig. S4†). Should Co(tpy)2 be the active catalyst, the addition of the 2nd equivalent of tpy would be expected to increase the catalytic current observed. Since the reverse is observed, this experiment supports the idea of an active catalyst containing less than 2 tpy per cobalt centre.
From this, and based on our previous study of CO2 reduction by Co–tpy, we conclude that it is likely that the active catalyst for the reduction of protons to hydrogen is comprised of one tpy per cobalt centre.
Possible mechanisms – quantification of the catalytic activity for hydrogen evolution by 1–5
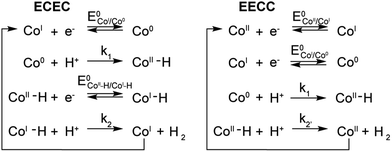
A few potential mechanisms are described below with the initial assumptions that all electron transfers occur at the electrode and a heterolytic mechanism is operative. The two main heterolytic mechanisms are schematically depicted in Scheme 2, without taking into account the localization of the electrons in the complex (i.e.: the species formally denoted Co0 could also be CoIL˙−). In the ECEC mechanism on the left, CoI is reduced to Co0, which undergoes protonation to form a CoII–H. This hydride is not sufficiently hydridic to be protonated efficiently and is reduced to a formally CoI–H. Subsequent protonation of the hydride yields H2 and CoI. The second mechanism, on the right, is an EECC mechanism, where the CoII species is sequentially reduced twice to generate a Co0 which can be protonated to form a CoII–H. In that case the latter is nucleophilic enough to react with a second proton thus forming H2 and CoII.To quantify the rates by which the HER occur for compounds 1–5 using cyclic voltammetry, the foot-of-the-wave analysis (FOWA) developed by Savéant et al. was performed.30FOWA was preferred to the ic/ip analysis that has been classically used in the literature31–33 because of the shape of the CVs observed. In the absence of the classical S-shaped curve with a fixed plateau current and overlapping forward and backward traces, the CVs near the peak are mostly under the influence of other factors, such as substrate consumption and diffusion. To circumvent this and estimate the rate constant for the HER, the CV is modelled near the foot of the wave, where these factors play a smaller role and the shape of the CV is dominated by the catalytic reaction.
It has to be noted that the rate constants determined by means of the FOWA here represent intrinsic rate constants, in the hypothetical scenario where the catalysis is not limited by side phenomena such substrate consumption. As such, there are most probably overestimations of the observed rate constant in bulk electrolyses, where the side phenomena might have a greater influence.
For a reversible homogeneous diffusion controlled one-electron transfer, the current at the peak is given by the Randles–Sevick equation:
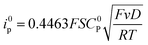 | (3) |
For a multi-step catalytic reaction following the two mechanisms depicted in Scheme 2, namely an EECC and a ECEC (where the second reduction event is easier than the first) where all electron transfers occur at the electrode, the expression of the current is given by the following equation:34,35
 | (4) |
 is the standard potential of the redox couple triggering catalysis.
is the standard potential of the redox couple triggering catalysis.
Since the surface of the electrode used is constant, and assuming that the diffusion coefficient of the complexes involved in the catalytic cycle are comparable, dividing (4) by i0p (eqn (3)) allows for a straightforward determination of kobs without prior need for determination of the diffusion coefficient or the electrochemically accessible surface of the electrode:
 | (5) |
Plotting i/i0p as a function of 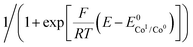 near the foot of the wave gives a linear function at a given scan rate (see ESI Fig. S5†). The observed rate constant kobs can then be extracted from the slope of the linear fit. For both mechanisms considered here kobs = k1 × C0A with k1 the rate constant for the hydride formation reaction and C0A the concentration of acid in the bulk solution. In the case of compounds 1–5, the rate constants were determined using the FOWA with a concentration of acetic acid of 60 mM and the analysis was repeated at 6 different scan rates in the 0.05–1 V s−1 range. The results are shown in Fig. 4.
near the foot of the wave gives a linear function at a given scan rate (see ESI Fig. S5†). The observed rate constant kobs can then be extracted from the slope of the linear fit. For both mechanisms considered here kobs = k1 × C0A with k1 the rate constant for the hydride formation reaction and C0A the concentration of acid in the bulk solution. In the case of compounds 1–5, the rate constants were determined using the FOWA with a concentration of acetic acid of 60 mM and the analysis was repeated at 6 different scan rates in the 0.05–1 V s−1 range. The results are shown in Fig. 4.
As expected, the rate constants are independent of scan rate (Fig. 4). In the case of compound 3, the same analysis was performed at 40 and 20 mM of acetic acid with scan rates of 0.05–1 V s−1 and the rate constant was shown to be independent of acid concentration as expected (ESI Fig. S6†). The average of the values obtained at the 6 different scan rates tested was used as k1: 6400 M−1 s−1 for 5, 1700 M−1 s−1 for 4, 1100 M−1 s−1 for 3, 200 M−1 s−1 for 2 and 100 M−1 s−1 for 1 (data showed in ESI Fig. S7 and 8†). Insights regarding turnover frequencies (TOF) values can then be derived from these numbers using the equation: TOFmax = k1C0A, but only if k1 can be considered rate-limiting. As detailed in the ESI (pp. S15–16†), the evaluation of the CVs for 3 confirms that indeed k1 is rate-determining. Thus maximum intrinsic turnover frequency TOFmax are given in Fig. 4 (right) for a concentration of acetic acid of 1 M. Comparison of the five complexes confirm that the more electron-donating the substituent, the better the catalyst is at hydrogen evolution from acetic acid in DMF in terms of maximal turnover frequency. If the protonation of a cobalt-hydride is invoked in the mechanism for hydrogen evolution, the hydridic nature of the hydride would be dictated by the electronic density on the metal centre. As more electron-donating substituents are on the ligands, the electronic density on the metal is expected to increase, yielding a hydride more reactive towards protonation.
In an effort to benchmark the activity of the complexes towards proton reduction and to compare them to other systems, a catalytic Tafel plot was generated (Fig. 5). The catalytic Tafel plot has been recently proposed by Savéant et al. as an efficient way to compare catalysts without having to depend so heavily on cell geometries used for bulk electrolyses.36 It consists of a plot of the log of TOF as a function of overpotential. As has been demonstrated elsewhere,35 the turnover frequency depends on the applied potential following eqn (6):
 | (6) |
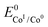 . In order to take into account the overpotential
. In order to take into account the overpotential 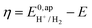 , with
, with  , the apparent redox potential for the reduction of the acid under consideration in the solvent studied, (6) can be reformulated as:
, the apparent redox potential for the reduction of the acid under consideration in the solvent studied, (6) can be reformulated as: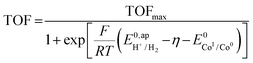 | (7) |
The logarithm of (7) is the equation of the catalytic Tafel plot. The catalytic Tafel plot can be generated from three parameters: TOFmax, 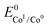 and
and  . We have previously determined TOFmax = k1C0A for a specifically chosen concentration of acetic acid, C0A = 1 M, (Fig. 4, right).
. We have previously determined TOFmax = k1C0A for a specifically chosen concentration of acetic acid, C0A = 1 M, (Fig. 4, right). 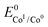 is determined from CVs in the absence of substrate (Fig. 1, ligand based feature, ESI Fig. S1†).
is determined from CVs in the absence of substrate (Fig. 1, ligand based feature, ESI Fig. S1†).  can be calculated using the following thermodynamic relationship (8):
can be calculated using the following thermodynamic relationship (8):
 | (8) |
 the thermodynamic potential for the reduction of protons to hydrogen in the solvent chosen. Following previously reported values, under our conditions
the thermodynamic potential for the reduction of protons to hydrogen in the solvent chosen. Following previously reported values, under our conditions 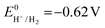 vs. Fc+/Fc, and pKDMFacetic acid = 13.5.37 These values are used to calculate
vs. Fc+/Fc, and pKDMFacetic acid = 13.5.37 These values are used to calculate 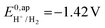 vs. Fc+/Fc.
vs. Fc+/Fc.
This catalytic Tafel plot representation allows for easy interpretation of the catalytic activity, and exemplifies the trade-off between overpotential and TOF of a catalytic system. While there only are a few examples of hydrogen evolution catalysts that have been studied using the FOWA analysis so far,36,38 we believe that this report of catalytic Tafel behaviour will prove useful for future comparative purposes as more catalytic Tafel plots are reported.
Study of complexes 1–5 as catalysts for CO2 reduction to CO
Compounds 1–5 were then assayed for CO2 reduction, in CO2-saturated DMF, with 5% of added water as a proton source to mimic the conditions of the previous report in which mixtures of CO and H2 were generated using compound 3 as a catalyst. The cyclic voltammograms, in Fig. 6, show that compounds 1, 2, 4 and 5 behaved as compound 3:16 two reversible one-electron diffusion-controlled waves under an inert atmosphere, as observed previously in dry DMF, and a strong cathodic current enhancement of the ligand-based system accompanied by loss of reversibility in CO2-saturated solutions. As shown below this corresponds to a catalytic process producing a mixture of CO and H2.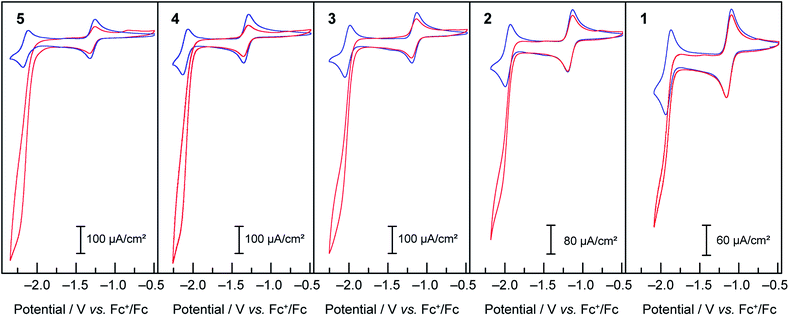 | ||
Fig. 6 Cyclic voltammograms under Ar ( blue) and CO2 ( blue) and CO2 ( red) at 50 mV s−1 of 1 mM solutions of compounds 1–5 in DMF/H2O (95 red) at 50 mV s−1 of 1 mM solutions of compounds 1–5 in DMF/H2O (95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5), TBAPF6 0.1 M. 5), TBAPF6 0.1 M. | ||
As observed during the study of the HER, complexes bearing more electron-donating groups on the ligands exhibit higher current enhancements, as well as a shift of the catalytic activity to more reducing potentials. To evaluate the range of the relative rate constants for CO2 reduction for 1–5, the FOWA was performed on CVs at different scan rates for each catalyst under catalytic conditions. The goal was to obtain an estimate of the maximal possible rate for the CO2 reduction catalytic process. The results of the FOWA (ESI Fig. S9–11†) indicate a range of second-order rate constants across the series from below 50 M−1 s−1 for 1 to over 350 M−1 s−1 for 5. Of importance, these values are upper estimates of the rate constants for CO2 reduction due to the presence of multiple electrochemical processes occurring within the catalytic feature of the CVs. These results give a quantitative description of the greater effect that electronic tuning of the ligand sphere has on proton reduction rates relative to CO2 reduction rates, as the rate constants for H2 evolution from acetic acid for the same catalysts series vary from 100 to over 6000 M−1 s−1. In both cases electron withdrawing groups also decrease the overpotential for the onset of catalysis, albeit at the expense of observed current densities.
To compare the activity of these compounds for the reduction of CO2, bulk electrolyses were performed with a fixed applied current. In order to control the kinetics of the system, a constant current of 300 μA was applied for 4 hours to 1 mM CO2-saturated solutions of compounds 1–5 in DMF/H2O (95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5) with 0.1 M of TBAPF6 as supporting electrolyte. Over the course of the experiment, the potential at the working electrode slowly decreased as all the CoII was reduced to CoI (0.77 C, 43 min), at which point a steady potential was observed, which remained constant throughout the rest of the experiment (ESI Fig. S12†). As expected, the more negative the potential of the ligand-based reduction, the more negative the potential at which the system equilibrated.
5) with 0.1 M of TBAPF6 as supporting electrolyte. Over the course of the experiment, the potential at the working electrode slowly decreased as all the CoII was reduced to CoI (0.77 C, 43 min), at which point a steady potential was observed, which remained constant throughout the rest of the experiment (ESI Fig. S12†). As expected, the more negative the potential of the ligand-based reduction, the more negative the potential at which the system equilibrated.
As was the case for a previous report involving compound 3, the only gaseous products observed were CO and H2.16 The faradic efficiencies for these products are given in Fig. 7. Since a constant current was applied during the experiments, the number of Coulombs passed over time was fixed and the absolute moles of product observed correlates directly to the faradic yields. The systems can thus be compared in terms of faradic yields or moles of product formed alike (ESI Fig. S13†).
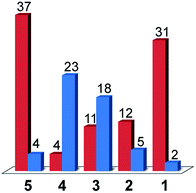
When considering only complexes 1–4, the catalysts that exhibited the lowest activity towards H2 evolution from acetic acid in DMF were found to be the most selective compounds for CO production over H2 evolution under CO2 reduction conditions. From compound 4 to compound 1, the faradic efficiency for CO production rose from 4% to 31%, while the efficiencies for H2 evolution dropped from 23% for 4 to 2% for 1. The strategy of tuning the electronics of the system to turn off hydrogen production thus yielded the results expected with compound 1 being the most selective CO2 reduction catalyst.
We have previously shown using catalyst 3 that the ratios of H2 to CO obtained in CO2 reduction catalytic conditions can be tuned by varying the applied potential.16 More specifically, forcing the system via increasing the overpotential favours H2 production with respect to CO2 reduction by increasing the total amount of H2 generated but virtually un altering the amount of CO generated. Interestingly, considering only complexes 1–4, we show here a similar qualitative behaviour wherein increasing the electron density on the metal centre, now using tpy-derived ligands with increasing electron-donating properties, results in enhanced H2 production thereby decreasing the ratio of CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 generated. Thus, in this particular case, increasing the reducing power of the system, while accelerating both reactions, has a greater effect on H+ reduction than on CO2 reduction in a similar manner as increasing the applied potential of a single system enhanced the amount of H2 generated while having little effect on the total amount of CO generated.
H2 generated. Thus, in this particular case, increasing the reducing power of the system, while accelerating both reactions, has a greater effect on H+ reduction than on CO2 reduction in a similar manner as increasing the applied potential of a single system enhanced the amount of H2 generated while having little effect on the total amount of CO generated.
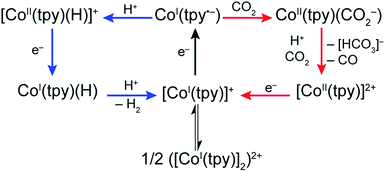
Our present data, together with previous reports, are consistent with a monotpy cobalt complex, CoI(tpy˙−), as the active catalytic intermediate, with product selectivity depending on the competition between reaction with H+ or CO2 (Scheme 3). Understanding the reason for electron-enriched tpy ligands affecting the two reactions so differently requires deep theoretical characterization of the electronic structure of the intermediate species as well as the activation energies of the reactions in both cases which are currently under investigation. However, we suggest that, to a first approximation, differences in coulombic repulsion of transition states can be invoked to explain the larger variations found in CoI(tpy˙−) interactions with H+ relative to interactions with CO2 upon changes in electronic structure of the ligand field. In considering proton reduction, the critical interaction is between a positively charged H+ atom and an electron-rich cobalt centre. As the cobalt centre is made less electron-rich through the incorporation of more electron-withdrawing tpy ligands, the coulombic repulsion between the cobalt centre and the H+ should be increased resulting in a higher activation barrier. In contrast, as CO2 is a neutral substrate, there should be minimal effect on the activation barrier between the cobalt centre and CO2 attributable to the cobalt centre becoming less electron-rich. While simply a first approximation, electronic repulsion forces have proven to significantly contribute to activation barriers for other reactions fully characterized by high level density functional theory.39
Whereas 1–4 clearly correlated to the aforementioned trend between proton reduction rate constants and selectivity for CO2 reduction, 5 surprisingly varied from the trend. The tpy ligand within 5, which includes three tBu groups, is the most electron-rich ligand of the series under study and as a consequence afforded the highest rates of H+ reduction (Fig. 2 and 4). Yet 5 only exhibited a faradic yield of 4% for H2 evolution under CO2 reduction conditions, despite its tremendous activity for hydrogen evolution from acetic acid in DMF. Along with this very small faradic efficiency for H2 production, 5 also exhibits the highest activity towards CO2 reduction to CO. It is tempting to consider that this is related to a steric effect as the functionalization of 5 is unique relative to the other complexes under study, with all three pyridine rings of the tpy ligand modified with larger tBu substituents. We have previously proposed a mechanism for CO2 reduction by 3 implying the formation of inactive dimeric species in the electrocatalytic reaction layer, in agreement with an apparent order in catalyst 3 of 0.5 in bulk electrolysis under electrocatalytic conditions.16 It is thus proposed that increased steric hindrance provided by tBu substituents on the tpy ligand disfavours the formation of the inactive dimer and thus greatly increases the concentration of the catalytically active mononuclear CoI(tpy˙−) intermediate. Accordingly, under CO2 reduction conditions, the reaction order in 5 was observed to be much closer to a traditional first order (ESI Fig. S14†).
However, simply increasing the concentration of a Co monotpy intermediate can only affect product selectivity if the dimeric species can also participate in a selectivity determining step. As mentioned before, the primary selectivity determining step is the relative interaction between CoI(tpy˙−) and either an equivalent of CO2 or an equivalent of H+. The observation of steric hindrance affecting selectivity by disfavouring H+ reduction suggests that the dimeric species can directly enter a proton reduction cycle via protonolysis. While speculative, this observation of a steric effect on product selectivity is unprecedented for CO2 reduction. Typically, the inclusion of functional groups within a ligand sphere to increase steric hindrance has been shown to increase overall rates of catalysis by either disfavouring the formation of inactive species or increasing the overpotential, but has not been shown to affect product selectivity. Despite falling outside the scope of the current manuscript, this report of the unexpected role of steric strain on product selectivity within the Co–tpy system clearly indicates a more complex reaction scheme relevant to selectivity and is motivation to continue to interrogate the role of steric hindrance on selectivity in the future.
Conclusions
In summary, we have reported the catalytic competency of catalysts 1–5 towards two reactions: the reduction of protons to H2, and the parallel reduction of CO2 and water to a mixture of CO and H2. Utilizing preparative scale electrolysis and the foot-of-the-wave analysis on cyclic voltammograms, the faradic yields for proton reduction and corresponding rate constants have been reported. A general trend is observed wherein faster rate constants are obtained with more electron rich ancillary ligands field, however at the expense of larger overpotentials. We have similarly evaluated the faradic yields and rate constants for CO2 reduction for the same series of catalysts and have observed a correlation between higher faradic yields for CO production with lower proton reduction rate constants. This represents the first report of a molecular system for which the selectivity towards CO2 reduction can be rationally optimized through disfavouring the HER. In agreement with this observation, utilizing the foot-of-the-wave analysis, we have demonstrated that electronic modifications to the ancillary ligand field have a much smaller effect on rate constants for CO2 reduction relative to rate constants for proton reduction. The less dramatic effect found for CO2 reduction rate constants upon ligand modifications validates the proposed strategy of “turning off” proton reduction in order to gain enhanced selectivity for carbon containing products for molecular CO2 reduction systems. Whereas transition state electronic repulsion arguments can be made to justify these results, a more thorough theoretical evaluation is currently under pursuit. Finally, we have also observed a novel steric effect on product selectivity through the inclusion of multiple tBu functional groups within the polypyridine ligands. Future work will be focused on better understanding this unique relationship between steric hindrance and product selectivity. We believe that these results and strategy validation are valuable to the rapidly growing area of molecular CO2 reduction catalysts development.Experimental section
General considerations
Unless otherwise noted, all solvents were purchased from Carlo Erba. Hexadistilled mercury was purchased from Ophram and annealed platinum wire was purchased from Alfa Aesar. Anhydrous N,N-dimethylformamide, cobalt(II) chloride, tetra-n-butylammonium hexafluorophosphate (TBAPF6), sodium methoxide, glacial acetic acid, ammonium hexafluorophosphate, 4′-chloro-2,2′:6′,2′′-terpyridine, 4′-(4-chlorophenyl)-2,2′:6′,2′′-terpyridine, 4,4′,4′′-tri-tert-butyl-2,2′:6′,2′′-terpyridine, 4′-(4-methylphenyl)-2,2′:6′,2′′-terpyridine and 2,2′:6′,2′′-terpyridine of the highest purity available were purchased from Sigma-Aldrich and used as received. 4′-Methoxy-2,2′:6′,2′′-terpyridine and compounds 1–5 were synthesized according to modified literature procedures.40–42All electrochemical data were referenced to the potential of the Fc+/Fc couple in the solvent system used and the IUPAC convention was used to report current.
Cyclic voltammetry experiments
All cyclic voltammetry experiments were carried out in a 10 mL single-compartment cell using a 3 mm diameter glassy carbon electrode (from Bio-Logic). The working electrode was polished before each measurement with a 1 μm diamond suspension. A Pt wire counter electrode was used, with a Ag/AgCl, 3 M NaCl reference electrode separated from the solution by a Vycor tip. IR drop was compensated to 85% using the ZIR built-in compensation method of the SP 300 Bio-Logic potentiostat. The supporting electrolyte used was tetrabutylammonium hexafluorophosphate (TBAPF6) at a concentration of 0.1 M. All solutions were thoroughly degassed with argon or CO2 before CVs were recorded.Bulk electrolysis experiments
Bulk electrolysis experiments were carried out in a custom made two-compartment cell (ESI Fig. S15†). The working electrode used was a 1.5 cm diameter pool of mercury, separated from the coiled annealed platinum wire counter electrode by a porous 4 frit, and the Ag/AgCl, 3 M NaCl reference electrode was separated from the solution by a Vycor tip. The supporting electrolyte used was TBAPF6 at a concentration of 0.1 M. The typical volume of solution used in the working compartment of the cell is 8 mL, and the typical headspace volume is 27 mL. A Bio-Logic SP 300 potentiostat connected to a booster card was used to apply a constant potential or constant current. Bulk electrolysis solutions were purged with inert gas (N2) or CO2 for at least 15 min prior to electrolysis and stirred throughout bulk electrolysis experiments.Chemical analysis
H2 and CO evolution were monitored by gas chromatography during bulk electrolyses by periodically sampling 50 μL of headspace. Measurements for H2 were performed by gas chromatography on a Shimadzu GC-2014 equipped with a Quadrex column, a Thermal Conductivity Detector and using N2 as a carrier gas. CO was measured using a Shimadzu GC-2010 Plus gas chromatography, fitted with a Restek Shin Carbon column, helium carrier gas, a methanizer and a Flame Ionization Detector. Gas chromatography calibration curves were made by sampling known volumes of CO and H2 gas respectively. The presence of other CO2 reduction products was assessed following previously reported methods.16Acknowledgements
We acknowledge support from Foundation de l'Orangerie for individual Philanthropy and its donors. This work was supported by the French National Research Agency (ANR, Carbiored ANR-12-BS07-0024-03) and the French State Program ‘Investissements d'Avenir’ (Grants “LABEX DYNAMO”, ANR-11-LABX-0011). N. E. acknowledges the Direction Générale de l'Armement (DGA) for a graduate research fellowship.Notes and references
- T. Faunce, S. Styring, M. R. Wasielewski, G. W. Brudvig, A. W. Rutherford, J. Messinger, A. F. Lee, C. L. Hill, H. deGroot, M. Fontecave, D. R. MacFarlane, B. Hankamer, D. G. Nocera, D. M. Tiede, H. Dau, W. Hillier, L. Wang and R. Amal, Energy Environ. Sci., 2013, 6, 1074 Search PubMed.
- T. R. Cook, D. K. Dogutan, S. Y. Reece, Y. Surendranath, T. S. Teets and D. G. Nocera, Chem. Rev., 2010, 110, 6474 CrossRef CAS PubMed.
- H. Arakawa, M. Aresta, J. N. Armor, M. A. Barteau, E. J. Beckman, A. T. Bell, J. E. Bercaw, C. Creutz, E. Dinjus, D. A. Dixon, K. Domen, D. L. DuBois, J. Eckert, E. Fujita, D. H. Gibson, W. A. Goddard, D. W. Goodman, J. Keller, G. J. Kubas, H. H. Kung, J. E. Lyons, L. E. Manzer, T. J. Marks, K. Morokuma, K. M. Nicholas, R. Periana, L. Que, J. Rostrup-Nielson, W. M. H. Sachtler, L. D. Schmidt, A. Sen, G. A. Somorjai, P. C. Stair, B. R. Stults and W. Tumas, Chem. Rev., 2001, 101, 953 CrossRef CAS PubMed.
- M. Rakowski DuBois and D. L. DuBois, Acc. Chem. Res., 2009, 42, 1974 CrossRef CAS PubMed.
- E. E. Benson, C. P. Kubiak, A. J. Sathrum and J. M. Smieja, Chem. Soc. Rev., 2009, 38, 89 RSC.
- A. J. Morris, G. J. Meyer and E. Fujita, Acc. Chem. Res., 2009, 42, 1983 CrossRef CAS PubMed.
- S. N. Riduan, Y. Zhang and J. Y. Ying, Angew. Chem., Int. Ed., 2009, 48, 3322 CrossRef CAS PubMed.
- C. Federsel, A. Boddien, R. Jackstell, R. Jennerjahn, P. J. Dyson, R. Scopelliti, G. Laurenczy and M. Beller, Angew. Chem., Int. Ed., 2010, 49, 9777 CrossRef CAS PubMed.
- C. Costentin, S. Drouet, M. Robert and J.-M. Saveant, Science, 2012, 338, 90 CrossRef CAS PubMed.
- M. Bourrez, F. Molton, S. Chardon-Noblat and A. Deronzier, Angew. Chem., Int. Ed., 2011, 50, 9903 CrossRef CAS PubMed.
- J. D. Froehlich and C. P. Kubiak, Inorg. Chem., 2012, 51, 3932 CrossRef CAS PubMed.
- J. Agarwal, T. W. Shaw, C. J. Stanton, G. F. Majetich, A. B. Bocarsly and H. F. Schaefer, Angew. Chem., Int. Ed., 2014, 53, 5152 CrossRef CAS PubMed.
- M. L. Clark, K. A. Grice, C. E. Moore, A. L. Rheingold and C. P. Kubiak, Chem. Sci., 2014, 5, 1894 RSC.
- J. A. Keith, K. A. Grice, C. P. Kubiak and E. A. Carter, J. Am. Chem. Soc., 2013, 135, 15823 CrossRef CAS PubMed.
- J. M. Smieja, E. E. Benson, B. Kumar, K. A. Grice, C. S. Seu, A. J. M. Miller, J. M. Mayer and C. P. Kubiak, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15646 CrossRef CAS PubMed.
- N. Elgrishi, M. B. Chambers, V. Artero and M. Fontecave, Phys. Chem. Chem. Phys., 2014, 16, 13635 RSC.
- C. W. Li, J. Ciston and M. W. Kanan, Nature, 2014, 508, 504 CrossRef CAS PubMed.
- A. Call, Z. Codola, F. Acuna-Pares and J. Lloret-Fillol, Chem.–Eur. J., 2014, 20, 6171 CrossRef CAS PubMed.
- M. Nippe, R. S. Khnayzer, J. A. Panetier, D. Z. Zee, B. S. Olaiya, M. Head-Gordon, C. J. Chang, F. N. Castellano and J. R. Long, Chem. Sci., 2013, 4, 3934 RSC.
- S. Varma, C. E. Castillo, T. Stoll, J. Fortage, A. G. Blackman, F. Molton, A. Deronzier and M.-N. Collomb, Phys. Chem. Chem. Phys., 2013, 15, 17544 RSC.
- T. Abe and M. Kaneko, J. Mol. Catal. A: Chem., 2001, 169, 177 CrossRef CAS.
- X. Chen, H. Ren, W. Peng, H. Zhang, J. Lu and L. Zhuang, J. Phys. Chem. C, 2014, 118, 20791 CAS.
- B. D. McCarthy, D. J. Martin, E. S. Rountree, A. C. Ullman and J. L. Dempsey, Inorg. Chem., 2014, 53, 8350 CrossRef CAS PubMed.
- A. E. King, Y. Surendranath, N. A. Piro, J. P. Bigi, J. R. Long and C. J. Chang, Chem. Sci., 2013, 4, 1578 RSC.
- K. A. Gheysen, K. T. Potts, H. C. Hurrell and H. D. Abruna, Inorg. Chem., 1990, 29, 1589 CrossRef CAS.
- D. Inoki, T. Matsumoto, H. Nakai and S. Ogo, Organometallics, 2012, 31, 2996 CrossRef CAS.
- H. P. Bennetto and E. F. Caldin, J. Chem. Soc. A, 1971, 2191 RSC.
- J. Prasad and N. C. Peterson, Inorg. Chem., 1969, 8, 1622 CrossRef CAS.
- I. M. Henderson and R. C. Hayward, J. Mater. Chem., 2012, 22, 21366 RSC.
- C. Costentin, S. Drouet, M. Robert and J.-M. Savéant, J. Am. Chem. Soc., 2012, 134, 11235 CrossRef CAS PubMed.
- S. Kal, A. S. Filatov and P. H. Dinoflo, Inorg. Chem., 2014, 53, 7137 CrossRef CAS PubMed.
- G. P. Connor, K. J. Mayer, C. S. Tribble and W. R. McNamara, Inorg. Chem., 2014, 53, 5408 CrossRef CAS PubMed.
- J. P. Bigi, T. E. Hanna, W. H. Harman, A. Chang and C. J. Chang, Chem. Commun., 2010, 46, 958 RSC.
- E. S. Rountree, B. D. McCarthy, T. T. Eisenhart and J. L. Dempsey, Inorg. Chem., 2014, 53, 9983 CrossRef CAS PubMed.
- C. Costentin and J.-M. Savéant, ChemElectroChem, 2014, 1, 1226 CrossRef CAS.
- V. Artero and J.-M. Savéant, Energy Environ. Sci., 2014, 7, 3808 CAS.
- V. Fourmound, P.-A. Jacques, M. Fontecave and V. Artero, Inorg. Chem., 2010, 49, 10338 CrossRef PubMed.
- D. J. Graham and D. G. Nocera, Organometallics, 2014, 33, 4994 CrossRef CAS.
- L.-P. Wang, Q. Wu and T. Van Voorhis, Inorg. Chem., 2010, 49, 4543 CrossRef CAS PubMed.
- R. S. Gaddie, C. B. Moss and C. M. Elliott, Langmuir, 2013, 29, 825 CrossRef CAS PubMed.
- P. Salvatori, G. Marotta, A. Cinti, E. Mosconi, M. Panigrahi, L. Giribabu, M. K. Nazeeruddin and F. De Angelis, Inorg. Chim. Acta, 2013, 406, 106 CrossRef CAS PubMed.
- J. Chambers, B. Eaves, D. Parker, R. Claxton, P. S. Ray and S. J. Slattery, Inorg. Chim. Acta, 2006, 359, 2400 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sc03766a |
| This journal is © The Royal Society of Chemistry 2015 |