Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational design of molecules for an all-quinone redox flow battery†
Süleyman
Er‡
ab,
Changwon
Suh‡
a,
Michael P.
Marshak
 a and
Alán
Aspuru-Guzik
*a
a and
Alán
Aspuru-Guzik
*a
aDepartment of Chemistry and Chemical Biology, Harvard University, 12 Oxford Street, Cambridge, MA 02138, USA. E-mail: aspuru@chemistry.harvard.edu
bLeiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands
First published on 21st November 2014
Abstract
Inspired by the electron transfer properties of quinones in biological systems, we recently showed that quinones are also very promising electroactive materials for stationary energy storage applications. Due to the practically infinite chemical space of organic molecules, the discovery of additional quinones or other redox-active organic molecules for energy storage applications is an open field of inquiry. Here, we introduce a high-throughput computational screening approach that we applied to an accelerated study of a total of 1710 quinone (Q) and hydroquinone (QH2) (i.e., two-electron two-proton) redox couples. We identified the promising candidates for both the negative and positive sides of organic-based aqueous flow batteries, thus enabling an all-quinone battery. To further aid the development of additional interesting electroactive small molecules we also provide emerging quantitative structure-property relationships.
Introduction
We recently demonstrated that quinones can be used as electroactive materials for stationary energy storage applications by creating an aqueous flow battery (AFB) based on the redox chemistry of the 9,10-anthraquinone-2,7-disulphonic acid (AQDS) and the Br2/Br− couple.1 Replacing expensive redox-active metals in AFBs with abundant, carbon-based molecules, such as quinones, can dramatically lower the cost of electricity storage, because they can potentially be sourced from petroleum or biological sources.1 In contrast with many aqueous inorganic redox couples, such as M3+/2+ (M = V, Cr, or Fe), quinones undergo two-electron redox events in aqueous solution, which can enable quinone-based flow batteries to achieve higher energy densities than the conventional metal-based flow batteries.2 Several previous studies have computationally investigated one-electron redox couples of quinones3–5 yet none of trials were systematically screened for the two-electron two-proton reduction potentials that would occur in the acid electrolyte of an AFB. At present, the compiled data of the experimental reduction potentials of 700 one-electron quinone couples is the most detailed source of information.6 In addition, the experimental aqueous solubility data of quinones is limited to benzoquinone, hydroquinone, and some –SO3H functionalized quinones.7–9The central aim of the present study is to systematically study the redox properties of a library of existing and non-existing quinone and hydroquinone derivatives and to investigate their quantitative structure–property relationships (QSPRs). Here, we use a virtual screening approach10–16 coupled with materials genomic concepts17–19 to allow for the rational design of an all-quinone flow battery.
Quinone–bromide flow batteries have been shown to reduce the cost of electrical energy storage by nearly an order of magnitude,1 and continued improvements in cell voltage and energy density could continue to drive the energy and power cost components down.20 Replacement of bromine with a quinone for the positive electrolyte would enable the use of low-cost storage tank, plumbing, and membrane materials.
Methodology
The combinatorial library of quinones/hydroquinones
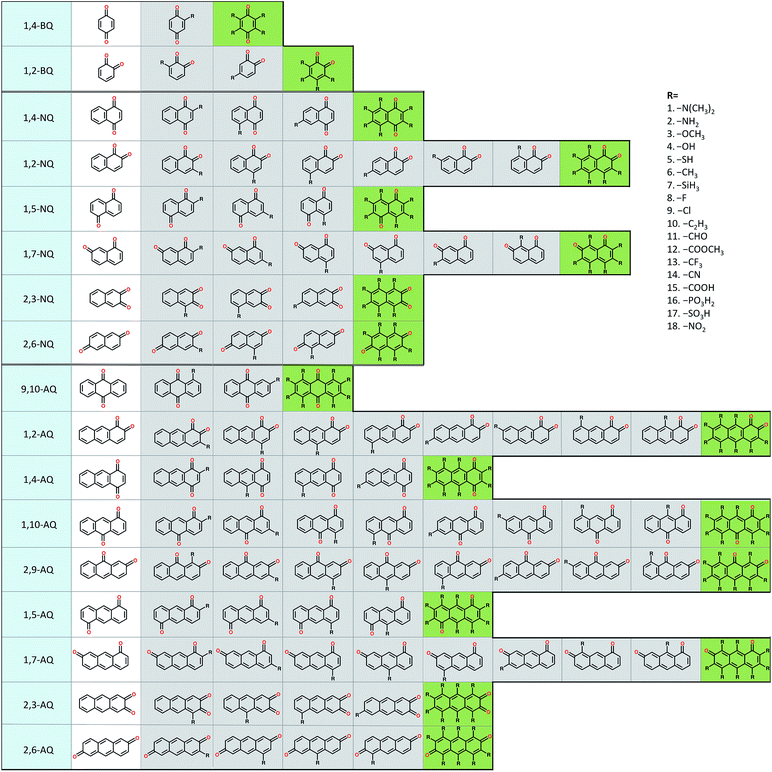
To explore the electrochemical properties of the candidate quinones we generated a virtual library of molecules by altering the core structures of quinones and by decorating quinone cores with interesting chemical substituents. The classes of 1-, 2-, and 3-ring quinone isomers are enumerated according to the position of the ketone groups on the pure quinones. The screening library also covers multiple ring quinone isomers that have the two cyclic ketone groups on different rings. Thus, the combinatorial library of the pure quinones contains 2, 6, and 9 different classes for benzoquinones (BQs), naphthoquinones (NQs), and anthraquinones (AQs), respectively (Fig. 1).We utilized the following R-groups as substituents, –N(CH3)2, –NH2, –OCH3, –OH, –SH, –CH3, –SiH3, –F, –Cl, –C2H3, –CHO, –COOCH3, –CF3, –CN, –COOH, –PO3H2, –SO3H, and –NO2. The position of substituents is known to affect the electrochemistry of quinones significantly.21–24 The effects of the incorporated R-groups on the redox potential (E0) of the quinone couples are investigated in two extreme conditions, i.e., the single and the full substitutions, since E0 and solvation free energy (ΔG0solv) of the intermediately substituted quinones would simply assumed to fall in between these two ends. For single substitutions, we systematically studied all possible substitution sites on a quinone. In the full substitution studies, all hydrogens of a quinone core are substituted with the same R-group. The combinatorial quinone library enumerates a total of 1710 quinone (Q)/hydroquinone (QH2) molecular couples.
High-throughput computational screening
The spatial positioning of the substituted (R) groups that enable new intramolecular hydrogen bonds is known to dramatically influence the calculated total free energies of the molecules.1,25 To accurately predict the ground state of a molecule, such as a quinone functionalized with sterically crowded and rotatable R-groups, it is useful to study many different conformers with quantum chemical methods. Taking into account of a trade-off between number of conformers (accuracy) and available computing power (resources), for our computational screening we generated a minimum of three low-energy conformers for each of the Q (oxidized) and the QH2 (reduced) molecules using a generic force field.26,27 Thus, the screening library contains more than 10000 virtual quinone derivatives in their Q and QH2 three-dimensional gas phase forms. The structural optimization of all of the conformers was carried out within the framework of the density functional theory (DFT). The DFT total energies of the fully optimized molecules are used to predict the E0 of the Q/QH2 couples. As a descriptor of solubility in aqueous media, we also utilized the optimized structures of the quinones to calculate the ΔG0solv. The entire high-throughput (HT) computational screening approach comprised approximately 33000 DFT simulations.The E0 of all of the Q/QH2 couples existing in the virtual library are predicted using the theoretical approach of the previous study.1 It is known that at low pHs, the reduction of a quinone to its hydroquinone requires two electrons and two protons.24 In a recent study, we confirmed the 2e−/2H+ process for the reduction of chemically functionalized 9,10-anthraquinones to 9,10-anthrahydroquinones.1 Accordingly, here, we assume that the reduction of a quinone is a single-step reaction involving a two-electron two-proton process.
Using E0 = −(nF)−1ΔHf + b, where n is the number of electrons, F is the Faraday constant, and b is a constant, we directly correlate the experimentally measured E0 of Q/QH2 couples in aqueous solutions to that of the heat of formation of hydroquinones at 0 K, ΔHf, from the quinones and the hydrogen gas.28 The calculation of ΔHf is based on the following reaction, where the two electrons and the two protons are replaced by a hydrogen molecule.
| Q + H2 → QH2 | (1) |
At T = 0 K, the calculation of ΔHf requires DFT total energies of quinones in their oxidized and reduced gas phase forms as well as the total energy of a hydrogen molecule. Because the entropies of reduction of quinones are found to be very similar, we neglected the entropy contributions on the free energies.28 As a training set for our calibration model, we utilized the experimental data on aqueous redox Q/QH2 couples29 and their DFT computed energies. ESI, Fig. S1† shows the robustness of the calibration model in predicting the E0 for a diverse set of quinones in different chemical solvents. The developed calibration model, based on the linear correlation (R2 = 0.974)1 between the calculated ΔHf and the measured E0(exp), provides an accelerated way to predict the E0(theo) for the 1710 Q/QH2 couples in the virtual library of quinones. A total of 10308 quinone and hydroquinone conformers were used as input structures for the DFT geometry optimizations, and the conformers with the lowest DFT total energies are then used to predict their ΔHf, which in turn are used to estimate E0 and ΔG0solv.
DFT calculations were carried out using the Perdew–Burke–Ernzerhof (PBE) functional of the generalized gradient approximation (GGA),30 the projector augmented wave (PAW) method,31,32 a plane-wave basis set, and the conjugate gradient (CG) algorithm, as implemented in the Vienna Ab initio Simulation Package (VASP).33,34 A cubic box of 25 Å along with the Γ-point sampling was used. The plane-wave kinetic energy cut-off was set at 500 eV. The convergence was assumed to be reached when the total remaining forces on the atoms were less than 10−2 eV Å−1.
In support of future synthesis efforts, it is desirable to identify the water soluble quinones. However, solubility is a complex function of crystal packing energy described by enthalpy of sublimation, cavitation energy, and solvation energy for interactions between solvent and solute.35 A major challenge is the determination of sublimation energy which is an arduous task due to the lack of well-defined structures and highly accurate periodic calculations.36 Palmer et al.'s work illustrates the difficulty in predicting solubility, even when using high-level theoretical calculations.37
In the current HT study, we treat the ΔG0solv as a descriptor of solubility in aqueous media. The ΔG0solv of the newly generated compounds is calculated by using the DFT ground state wave functions (PBE/6-31G**) and a Poisson–Boltzmann solvation model.38–40 This offers a compromise between the speed and the accuracy for our calculations. The ΔG0solv of a compound is the difference between the total energy of the solvated form and the total energy of the gas phase form. Thus, a negative value of ΔG0solv relates to a quinone with good aqueous solubility. We calculated ΔG0solv only for the oxidized form of quinones, since they would expected to be less soluble than their respective hydroquinones in water.
Results and discussion
Distributions of E0 and ΔG0solv of the screened virtual library
The distribution of the predicted E0 values between the Q/QH2 redox couples for the entire list of compounds existing in the virtual chemical library is shown in Fig. 2. By choosing Q/QH2 couples below 0.2 V for the negative and above 0.9 V for the positive sides of AFB, a practical battery voltage greater than 0.7 V is obtained. Based on the average E0 values, the 9,10-AQ derived quinones are found to be most suitable for the negative side of AFBs, whereas the 1,2-BQ, 2,3-NQ, and 2,3-AQ derivatives are found to be appropriate for the positive side of AFBs.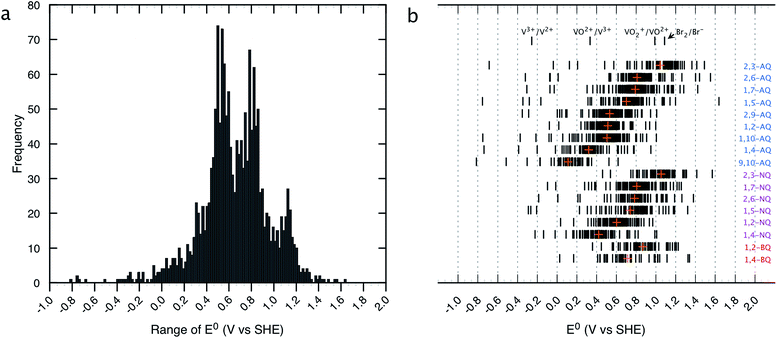 | ||
| Fig. 2 Distribution of HT screened quinone/hydroquinone redox couples. (a) A histogram of theoretically predicted E0 (V vs. SHE). Number of bins and width of the histogram are 130 and 0.1 V, respectively. (b) E0 windows for the different classes of quinones. The orange crosses show the mean values of E0 for each class. Redox potentials of the conventional inorganic AFB redox couples are noted for comparison.43 | ||
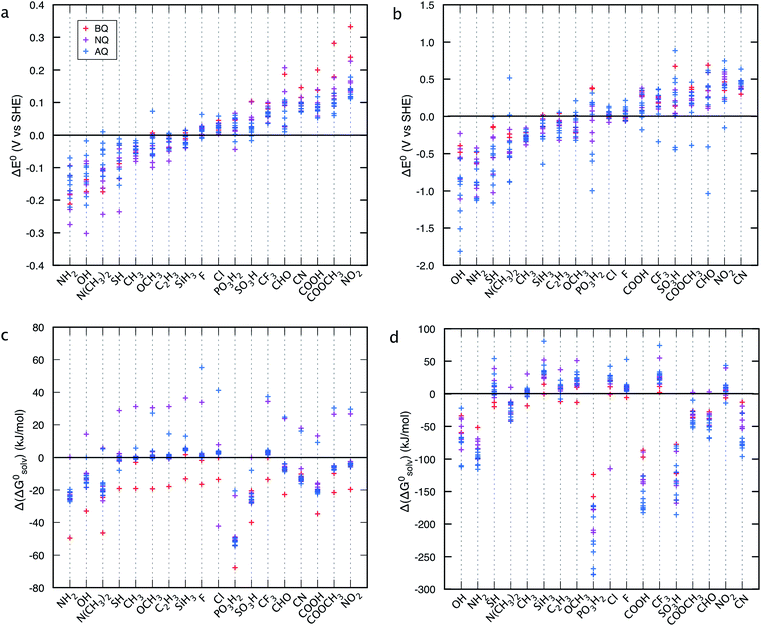
Fig. 3 shows that irrespective of the number of rings, functionalization of the quinones with the electron-donating groups (EDGs), such as –OH and –NH2, decreases the electron affinity of the compounds and results in low E0 values. Functionalization of quinones with electron-withdrawing groups (EWGs), such as –SO3H, –PO3H2, and –NO2, shows an opposite effect and results in high E0 values.21Fig. 3 also shows that substituting quinone core hydrogens with any R-group lowers the ΔG0solv of the majority of the molecules. Thus, as a first approximation, we expect that the functionalized molecules would be more soluble than their parent quinone compounds. As shown in Fig. 3, for quinones of all sizes, incorporating the –OH, –NH2, –COOH, –SO3H, and –PO3H2 groups into the pure quinone backbones significantly decrease the ΔG0solv, and therefore these groups are predicted to increase the aqueous solubility the most. In particular, the hydrogen bonding ability, acidity, and polarity of the –SO3H and –PO3H2 groups are especially well-suited to achieve high aqueous solubility.1,41,42
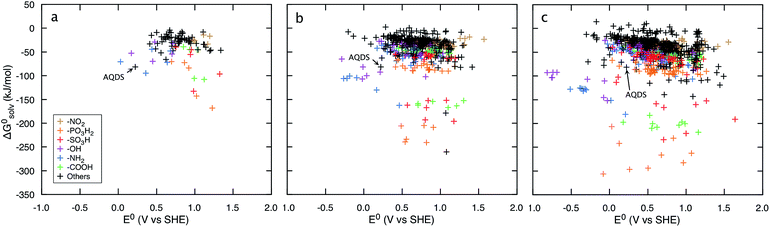 | ||
| Fig. 3 Redox-solubility maps of quinones of different sizes. E0 and ΔG0solv distributions of (a) BQs, (b) NQs, and (c) AQs. The functional groups that effectively tune the E0 and ΔG0solv are highlighted in color. AQDS molecule, which was successfully used for the negative side of an aqueous flow battery due to its low value of E0 (0.222 V: calculated and 0.213 V: measured) as well as a high aqueous solubility (greater than 1 M at pH 0),1 is marked as reference point. | ||
Structure–property relationships of quinones/hydroquinones
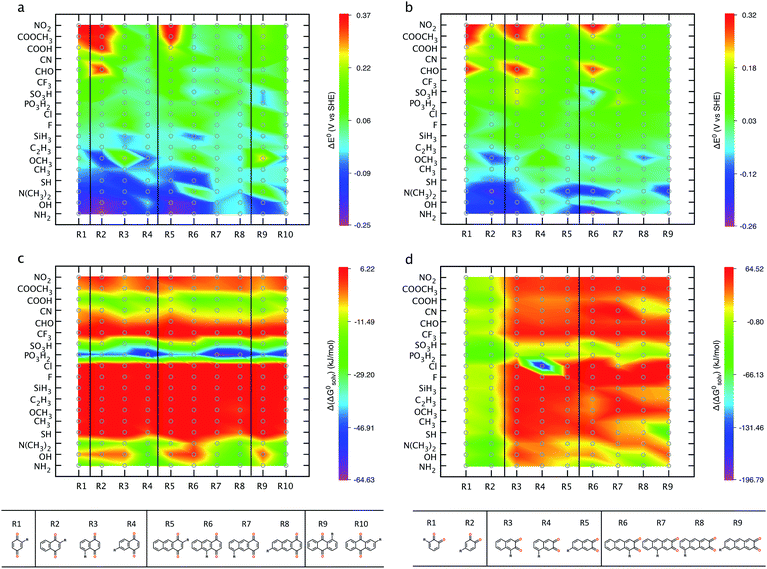
Structure–property relationships (SPRs) are useful for identifying the relationships between the new quinones and their chemical properties.8 SPRs provide beneficial information for fine-tuning the key properties of the candidate materials beyond the scope of the virtual library. In the present study, SPRs are identified quantitatively (i.e., QSPRs) and they suggest: (i) general relationships between the core structures of different classes of quinones, the type of substituents, the positions of substituents, and their predicted properties; and (ii) the key substituents and their positions with respect to redox behaviors in a given quinone library.Fig. 4 shows the change in theoretically predicted redox potentials (ΔE0) and solvation free energies (Δ(ΔG0solv)) with respect to the pure parent quinones, after the quinones are functionalized with the R-groups. A positive value of ΔE0 shows an increase in the redox potential, whereas a negative value of Δ(ΔG0solv) shows an increase in the solubility. The calculation methodology is given in ESI, Fig. S2.†Fig. 4a and b show the ΔE0 between the possible isomers of BQs, NQs, and AQs and their 18 different R-group functionalized forms. Fig. 4a shows the ΔE0 when the quinone/hydroquinone couples are decorated with a single R-group. For the parent quinones with multiple core hydrogen atoms that can be substituted in turn with a unique R-group, the ΔE0 shows the mean value of the change in E0 for all the possible substitutions.
Similarly, Fig. 4b shows the ΔE0 when the quinone/hydroquinone couples are functionalized fully via the substitution of all the quinone core hydrogens for the same R-group. The R-groups in the abscissa of Fig. 4 are ordered according to increasing mean value of ΔE0 of the same R-group substituted Q/QH2 molecules.
When compared to single substitutions, wider windows of E0 and ΔG0solv are achieved by substituting all of the quinone core hydrogens with R-groups (Fig. 4b and d). As shown in Fig. 4c and d the side chains of –OH, –NH2, –COOH, –SO3H, and –PO3H2 are useful in increasing the water solubility of the quinones. The ordering of functional groups correlates with the nature of EDGs and EWGs, and trends from molecular induction theories and Hammett parameters.44 EDGs, such as –OH and –NH2, decrease the E0 significantly when compared to their parent quinones with no side chains. Conversely, EWGs, such as –SO3H, –PO3H2, and –NO2 are useful in increasing the E0.
Fig. 5 provides a thorough investigation of the gross features of single R-group functionalized quinones. As shown in Fig. 5a and b irrespective of the class of quinone, EDGs groups, such as –OH, –NH2, and –N(CH3)2, are effective in decreasing the E0, whereas EWGs, such as –COOH, –CHO, –PO3H2, –COOCH3, –SO3H, –CF3, –CN, and –NO2 are useful in increasing the E0. The effects of EDGs on decreasing the E0 are particularly notable for the class of 1,5-NQ, whereas the effects of EWGs on increasing the E0 are remarkable especially for both of the two classes of BQs.
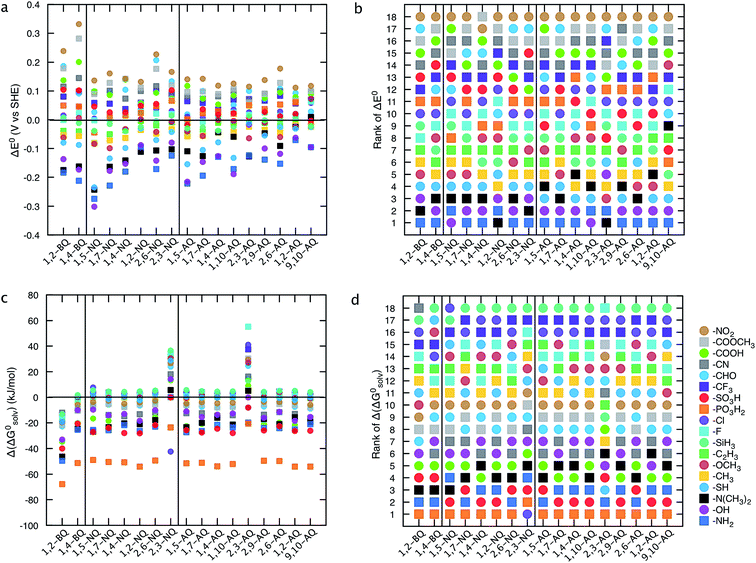 | ||
| Fig. 5 Effects of single R-group substitutions on tuning the redox potential and the solubility of different quinone classes. (a) Change in redox potential, ΔE0, (c) change in solvation free energy, Δ(ΔG0solv) for only a single R-group functionalized quinones. The mean values are reported when the functional group is substituted in turn with different core hydrogens of a parent quinone. (b and d) Ranking of substituents in affecting the E0 and ΔG0solv. The ranking is based on the efficiency of R-groups on decreasing the E0 (b) or ΔG0solv (d). The results of the fully functionalized quinones are shown in ESI, Fig. S3.† | ||
Functionalization of quinones with –PO3H2, –SO3H, –NH2, and –N(CH3)2 groups is expected to increase the predicted solubility of all quinone classes (Fig. 5c). Due to the simple solvation model employed and the fact that solid-state structures are not considered, the solubility predictions are qualitative, yet serve as a guiding tool for experimental synthesis. Fig. 5b and d show the ranking of the R-groups in decreasing the redox potential and increasing the solubility of the parent quinones. The HT analysis of the effects of R-group substitutions on the E0 and ΔG0solv shown in Fig. 5 effectively captures the features of R-group functionalization for each different class of quinones and provides a valuable primary guide for the future synthesis of the new compounds.
A critical factor in tuning the electrochemical properties of quinones is the position of the substituted groups on the quinone backbones.4,22,23 As a paradigmatic example, Fig. 6 shows the position effects on the E0 and the (ΔG0solv) of the R-group functionalized para- and ortho-quinones of multiple rings. Fig. 6a shows that –NH2 and –OH functional groups are efficient in decreasing the redox potential. Our further investigation of the position of the newly incorporated side groups shows that the E0 is remarkably affected by the distance between the newly substituted units and the cyclic ketone units of parent quinones.
As shown in Fig. 6a, incorporation of –NH2 or –OH into the para-quinones lowers the E0 with the following order: R2 ≫ R3 > R4 in 1,4-NQ, R5 ≫ R6 > R7 ∼ R8 in 1,4-AQ, and R9 > R10 in 9,10-AQ. A similar positional dependency of E0 is evident for the –NH2 and –OH substituted ortho-quinones (Fig. 6b). In agreement with a previous experimental study,45 the substitution of –OH groups adjacent to the ketone decreases E0 more effectively than their substitution with remote benzenoid ring hydrogens. Similarly, the effects of –CHO, –CN, –COOH, –COOCH3, and –NO2 groups on increasing the redox potential are increased when these groups are substituted for the quinone hydrogens adjacent to the ketone units, such as R2 in 1,4-NQ, R5 in 1,4-AQ, and R9 in 9,10-AQ (Fig. 6a), and similarly for ortho-quinones R1 in 1,2-BQ, R3 in 2,3-NQ, and R6 in 2,3-AQ (Fig. 6b).
Fig. 6c shows that for para-quinones, the substitutions of –NH2, –OH, –N(CH3)2, –PO3H2, –SO3H, and –COOH groups are predicted to improve the solubility, especially when they are placed further away from the cyclic ketone units of the parent quinones. Functionalization of the positions R4 in 1,4-NQ, R7 and R8 in 1,4-AQ, and R10 in 9,10-AQ, are predicted to have the greatest effect in decreasing the solvation free energies (i.e., augmented solubility). As shown in Fig. 5c, substitutions of most R-groups in 2,3-NQ and 2,3-AQ increase the value of ΔG0solv, thus the positional effects on the ΔG0solv are not clearly visible (Fig. 6d).
In an effort to guide future work on small organic molecule based AFBs, here, we summarize the key findings of our HT screening and QSPR analysis. First, we identified 104 Q/QH2 couples with E0 lower than 0.2 V vs. SHE, and 304 Q/QH2 couples with E0 higher than 0.9 V vs. SHE. As a reference data, the full list of interesting candidate molecules is given in ESI, Table S1.† Using the key findings of our HT screening, QSPR analysis, and our own chemical intuition of some of the expected behaviors of substituted quinones, such as the stability in water solution and the synthetic feasibility, we identified a shorter list of compounds. We also focused on compounds that have solvation free energy below a certain threshold (i.e. <−81.5 kJ mol−1, that is the calculated value of AQDS's solvation free energy in water.1) As a result, we shortlisted 31 quinones with redox potentials < 0.2 V and 28 quinones with > 1.0 V. These highly promising molecules are marked with an asterisk in ESI, Table S1.† Second, the class of 9,10-AQs is a suitable target for the negative side of an AFB cell, whereas the classes of 1,2-BQs, 2,3-NQs, and 2,3-AQs are more appropriate for the positive side of the cell (Fig. 1b). Third, utilizing EDGs (–OH and –NH2) decreases E0 of the pure quinones, thus making them more attractive for the negative side of an AFB. In contrary, utilizing EWGs (–SO3H, –PO3H2, and –NO2) increases E0 of the parent quinones, thus making them more attractive for the positive side of an AFB (Fig. 4a and b). Fourth, the effects of EDGs, such as –NH2 and –OH, in decreasing the E0 are increased when these groups are positioned close to the quinone ketone groups. Similarly, the effects of EWGs, such as –NO2, –COOCH3, –COOH, –CN, and –CHO, in increasing the E0 are increased when they are positioned close to the ketone groups (Fig. 6a and b). Fifth, substitutions of hydrophilic groups such as –OH, –NH2, –COOH, –SO3H, and –PO3H2 are predicted to increase the solubility. In general, full substitutions are more useful than single substitutions in improving the water solubility (Fig. 4c and d). The highly substituted quinones may have relatively lower synthetic accessibility due to steric hindrance. Last, good aqueous solubility can be achieved by substituting quinone hydrogens that are far from the quinone ketone groups with hydrophilic functional groups, such as –SO3H, and –PO3H2 (Fig. 6c and d).
Stability of molecules for energy storage
Given the huge number of organic molecules to be screened, we utilized HT computational screening strategies to reduce the search space of substituted quinones in this study. The ultimate goal of this study is to discover promising molecules for long-term energy storage. Stability is important not only to prevent chemical loss for long cycle life, but also because reaction with the electrode can compromise the electrode's conductivity and surface area.From a system's point of view, the use of quinones offers an advantage in stability over current flow battery technologies, because the quinone can exhibit minimal membrane crossover.1 On the other hand, the use of oxidizing quinones generates the possibility for decomposition reactions such as polymerization and oxidation of the carbon backbone. These limitations can be mitigated by replacing C–H groups adjacent to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups (vulnerable to oxidation) with groups such as C–R, where R is hydroxyl, sulfonyl, amino, or carboxyl.
O groups (vulnerable to oxidation) with groups such as C–R, where R is hydroxyl, sulfonyl, amino, or carboxyl.
From the computation point of view, predicting the stability of a molecule is challenging because of the many possible decomposition reactions and products. These sort of computations can be implemented in HT screening by identifying and screening for indicators of reactivity, which would initially be identified through experiments. One way that the stability of a molecule can be quantified is by calculating the rate at which it goes over the lowest barrier separating it from its isomerization or dissociation products. Alternatively, comparison of the frontier orbitals (i.e. the highest occupied molecular orbital, HOMO, and the lowest unoccupied molecular orbital, LUMO) or Fukui functions46 of the new molecules with those of stable quinones (such as AQDS) could predict their reactivity with electrophiles and nucleophiles, because—to a first approximation—the reactivity will be governed by the energies of these orbitals. Decomposition pathways due to solvent pH effects and electrical bias are also important future research directions.
Conclusions
We demonstrate the use of robust HT theoretical calculations as a fast screening tool for the discovery and the future design of potentially interesting quinone molecules for organic-based AFBs. The QSPR analysis presented in this study underlies the use of AQDS/AQDSH2 organic couple at the negative side of an AFB in our recent study.1 In this study, the predicted E0 values of Q/QH2 redox couples serve as a pivotal reference data for the target electrochemical window of a full-cell organic AFB. Moreover, the key finding that functionalization near to the ketones impacts reduction potential and away from the ketone improves solubility will be critical to further tuning the properties of new quinone electrolytes. The identification of over 300 quinones with a predicted reduction potential above 0.7 V and the refined list of synthetically feasible quinones should lead the way to a high-performance all-quinone flow battery, which is predicted to vastly reduce the cost of electrical energy storage.Author contributions
SE and CS contributed equally to this work. AAG conceived the project. SE and CS carried out the research, with direction from AAG. SE and CS were responsible for the generation of candidate materials library, theoretical screening of the candidate materials, and managing of results. SE and CS carried out the structural analysis of the top candidates with contributions from MPM. MPM's input was crucial for experimental assessment and for keeping a close loop with experimental parameters. SE and CS wrote the manuscript with contributions from MPM and AAG.Acknowledgements
This work was partially funded by means of the U.S. DOE ARPA-E award # DE-AR0000348. S.E. performed work as part of the Fellowships for Young Energy Scientists program of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organization for Scientific Research (NWO). The computing time was provided by Harvard FAS Research Computing, the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by U.S. NSF grant # ACI-1053575, and the Center for Functional Nanomaterials, Brookhaven National Laboratory, which is supported by the U.S. DOE, Office of BES, under contract # DE-AC02-98CH10886. We thank Roy G. Gordon and Michael J. Aziz for helpful discussions.Notes and references
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. P. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198 CrossRef CAS PubMed.
- R. F. Service, Science, 2014, 344, 352–354 CrossRef CAS PubMed.
- M. Namazian and M. L. Coote, J. Phys. Chem. A, 2007, 111, 7227–7232 CrossRef CAS PubMed.
- X. Zhu and C. Wang, J. Org. Chem., 2010, 75, 5037–5047 CrossRef CAS PubMed.
- J. Bachman, L. Curtiss and R. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860 CrossRef CAS PubMed.
- P. Wardman, J. Phys. Chem. Ref. Data, 2011, 18, 1637–1755 CrossRef PubMed.
- F. S. Granger and J. M. Nelson, J. Am. Chem. Soc., 1921, 43, 1401–1415 CrossRef CAS.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. K. Surya Prakash and S. R. Narayanan, J. Electrochem. Soc., 2014, 161, A1371–A1380 CrossRef CAS PubMed.
- T. Tomai, S. Mitani, D. Komatsu, Y. Kawaguchi and I. Honma, Sci. Rep., 2014, 4, 3591 Search PubMed.
- J. Hachmann, R. Olivares-Amaya, A. Jinich, A. Appleton, M. Blood-Forsythe, L. Seress, C. Román-Salgado, K. Trepte, S. Atahan-Evrenk, S. Er, S. Shrestha, R. Mondal, A. Sokolov, Z. Bao and A. Aspuruk, Energy Environ. Sci., 2014, 7, 698–704 CAS.
- E. Pyzer-Knapp, H. Thompson, F. Schiffmann, K. Jelfs, S. Chong, M. Little, A. Cooper and G. Day, Chem. Sci., 2014, 5, 2235–2245 RSC.
- D. Musumeci, C. A. Hunter, R. Prohens, S. Scuderi and J. F. McCabe, Chem. Sci., 2011, 2, 883–890 RSC.
- B. Seger, I. Castelli, P. Vesborg, K. Jacobsen, O. Hansen and I. Chorkendorff, Energy Environ. Sci., 2012, 7, 2397–2413 Search PubMed.
- C. E. Wilmer, M. Leaf, C. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- J. K. Nϕrskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- http://www.whitehouse.gov/blog/2011/06/24/materials-genome-initiative-renaissance-american-manufacturing, accessed 15 November 2014.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- G. L. W. Hart, Nature, 2012, 491, 674–675 CAS.
- M. Carbajales-Dale, C. J. Barnhart and S. M. Benson, Energy Environ. Sci., 2014, 7, 1538–1544 CAS.
- Y. Song and G. R. Buettner, Free Radical Biol. Med., 2010, 49, 919–962 CrossRef CAS PubMed.
- P. Manisankar and S. Valarselvan, Ionics, 2012, 18, 679–686 CrossRef CAS PubMed.
- D. Ajloo, B. Yoonesi and A. Soleymanpour, Int. J. Electrochem. Sci., 2010, 5, 459–477 CAS.
- P. S. Guin, S. Das and P. Mandal, Int. J. Electrochem., 2011, 816202 CAS.
- R. Qu, H. Liu, M. Feng, X. Yang and Z. Wang, J. Chem. Eng. Data, 2012, 57, 2442–2455 CrossRef CAS.
- S. L. Mayo, B. D. Olafson and W. A. Goddard III, J. Phys. Chem., 1990, 94, 8897–8909 CrossRef CAS.
- Marvin 6.1.0, ChemAxon, http://www.chemaxon.com Search PubMed.
- M. J. S. Dewar and N. Trinajstic, Tetrahedron, 1969, 25, 4529–4534 CrossRef CAS.
- J. R. T. J. Wass, E. Ahlberg, I. Panas and D. J. Schiffrin, J. Phys. Chem. A, 2006, 110, 2005–2020 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- C. A. Lipinski, F. Lombardo, B. W. Dominy and P. J. Feeney, Adv. Drug Delivery Rev., 2001, 46, 3–26 CrossRef CAS.
- D. S. Palmer, J. L. McDonagh, J. B. O. Mitchell, T. van Mourik and M. V. Fedorov, J. Chem. Theory Comput., 2012, 8, 3322–3337 CrossRef CAS.
- D. S. Palmer, A. Llinàs, I. Morao, G. M. Day, J. M. Goodman, R. C. Glen and J. B. O. Mitchell, Mol. Pharmaceutics, 2008, 5, 266–279 CrossRef CAS PubMed.
- D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, B. Honig, M. Ringnalda and W. A. Goddard III, J. Am. Chem. Soc., 1994, 116, 11875–11882 CrossRef CAS.
- B. Marten, K. Kim, C. Cortis and R. A. Friesner, J. Phys. Chem., 1996, 100, 11775–11788 CrossRef CAS.
- The Jaguar 8.0 program and the Schrödinger suite, 2012 Search PubMed.
- E. M. Thurman, Organic Geochemistry of Natural Waters, Kluwer Academic Publishers, Hingham, 1985, p. 94 Search PubMed.
- S. Li, Z. Zhou, H. Abernathy, M. Liu, W. Li, J. Ukai, K. Hase and M. Nakanishi, J. Mater. Chem., 2006, 16, 858–864 RSC.
- Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef CAS PubMed.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- J. B. Conant and L. F. Fieser, J. Am. Chem. Soc., 1924, 46, 1858–1881 CrossRef CAS.
- P. Geerlings, F. D. Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The list of computationally predicted candidate quinone molecules with interesting redox properties. See DOI: 10.1039/c4sc03030c |
| ‡ Authors with equal contribution to this work. |
| This journal is © The Royal Society of Chemistry 2015 |