Open Access Article
Open Access ArticleStepwise isolation of low-valent, low-coordinate Sn and Pb mono- and dications in the coordination sphere of platinum†
Holger
Braunschweig
*a,
Mehmet Ali
Celik
a,
Rian D.
Dewhurst
a,
Magdalena
Heid
a,
Florian
Hupp
a and
Sakya S.
Sen
b
aInstitut für Anorganische Chemie, Julius-Maximilians-Universität Würzburg, Am Hubland, 97074 Würzburg, Germany. Web: http://www-anorganik.chemie.uni-wuerzburg.de/Braunschweig/E-mail: h.braunschweig@uni-wuerzburg.de
bCSIR-National Chemical Laboratory, Pashan, Pune 411008, India
First published on 15th October 2014
Abstract
Synthetic access to low-coordinate Pb mono- and dications is in general impeded due to their poor solubility and highly electrophilic nature. However, the electrophilicity of these cations can be tamed by attaching them to electron-rich transition metals. Following this principle we have isolated low-valent Pb mono- ([(Cy3P)2Pt–PbCl]2[AlCl4]2, 8a) and dications ([(Cy3P)2Pt(Pb)][AlCl4]2, 11) in the coordination sphere of platinum. The same approach then has been implemented for the isolation of analogous low-valent Sn mono- (7a) and dications (10). An energy decomposition analysis (EDA-NOCV) was performed to investigate the nature of Pt–Pb and Pb–Cl bonding in [(Cy3P)2Pt(PbCl2)] (2), 8a and 11. The results show that the Pt–Pb bonds in 8a and 11 are electron-sharing in nature, whereas that of the precursor 2 is a dative bond. The breakdown of attractive interactions in 2, 8a and 11 reveals that the ionic interactions in the analyzed Pt–Pb and Pb–Cl bonds are always stronger than the covalent interactions, except for the Pb–Cl bond in 8a. The calculated D3 dispersion energies show that dispersion interactions play a key role in the thermodynamic stability of 2, 8a and 11.
Introduction
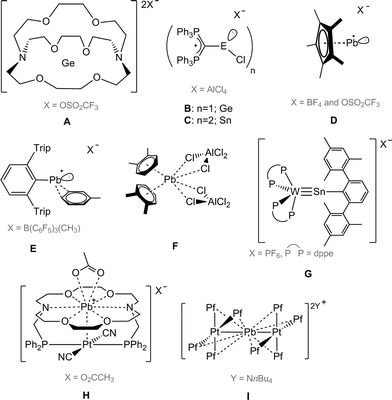
Following the isolation of a series of cations of composition [(C5Me5)E:]+ (E = Si–Pb) by Jutzi and co-workers,1 the synthesis and structural elucidation of divalent group 14 cations and dications has become a subject of considerable current interest. Recent isolation of a Ge(II) dication encapsulated within a cryptand (A, Scheme 1) by Baines et al. and carbodiphosphorane-stabilized [GeCl]+ (B) and [(SnCl)2]2+ (C) accentuates the ongoing growth of the chemistry of tetrylene(ii) cations.2,3 Much of this interest stems from the fact that the central atom in these salts carries two unoccupied valence orbitals as well as a lone pair of electrons. Such an electronic description suggests ambiphilicity, making them potentially interesting candidates for noninnocent (i.e. both σ-donating and π-accepting) ligation to transition metals – a topic of great interest for catalysis. Accordingly, the successful synthesis of divalent group 14 cations has required the design of new synthetic strategies based upon sterically-demanding neutral (cryptand, N-heterocyclic carbene, carbodiphosphorane) or monoanionic (β-diketiminate, cyclopentadienyl, N-isopropyl-2-(isopropylamino)troponimine, cyclophane, etc.) ligands, the utilization of counteranions, and solvents with low nucleophilicity in order to avoid their coordination to the cation. Noteworthy in this context is the work of the groups of Baines, Driess, Jones, Müller, Krossing, and others who have reported a plethora of such species.4–13In stark contrast to the foregoing, only a handful of low-coordinate lead(II) cations have been experimentally realized. Their isolation at ambient temperature is hindered by the highly electrophilic nature of these species. Jutzi and Nöth reported the first cationic Pb(II) compounds of the type [η5-Cp*Pb]+X− (D) (X = BF4 and OSO2CF3).14 Following this, Power published the synthesis of a lead(II) cation supported by a bulky terphenyl substituent (E), which is weakly coordinated by a toluene molecule.15 Very recently, Fulton and co-workers isolated two more Pb(II) cations stabilized by bulky β-diketiminato ligands.16 Apart from these, a few dications of lead have been realized through σ- or π-donating (N–, O–, or S–) atoms or by chelating ligands such as tmeda, bipyridine etc.17–19 Higher-coordinate lead(II) dications with weak arene interactions stabilized by chloride anions are also known,20,21 for example [(1,2-C6H4Me2)2Pb(AlCl4)2] (F).22 However, such stabilization occurs at the expense of the degree of the cationic character of the Pb atom, thus leading to an increase in its coordination number (six to eight). As a result, such species cannot be classified as low-coordinate cations. In order to realize a [LPb-Cl]+ or [LPb]2+ moiety, the use of a neutral ligand such as N-heterocyclic carbenes, carbodiphosphoranes or others seems logical, as they do not contribute to the formal charge or oxidation state of the central atom. However, to the best of our knowledge, reports of cationic lead(II) compounds containing such ligands have thus far not appeared (Scheme 1).
It was only recently that Filippou et al. reported another approach, in which the coordination sphere of late transition metals was employed to stabilize germanium(II)23 and tin(II) cations. Thereby, complexes such as [(Ph2PCH2CH2PPh2)2WSn–C6H3-2,6-Mes2][PF6] (G),24 as well as the molybdenum plumbylidyne complex trans-[Br(Me3P)4MoPb(C6H3-2,6-Trip2)] (Trip = 2,4,6-iPr3-C6H2),25 among others, were isolated. A few lead(II) dications in the coordination sphere of a late transition metal have been reported, albeit stabilized by chelating N-, and O-donor ligands (phenanthroline and diaza-18-crown-6)26 such as [(CH3CO2)Pb(crown-P2)Pt(CN)2][(O2CCH3)] (H),27 or [{Pt(C6F5)4}2(Pb)][nBu4N]2 (I) showing interaction with numerous fluorine atoms.28
Our aim was to establish a transition metal scaffold that would stabilize low-coordinate Sn(II) and Pb(II) cations and dications. Consequently, we turned our attention towards the electron-rich, coordinatively unsaturated complex [(Cy3P)2Pt] (1) as it (i) has shown an impressive ability to stabilize reactive main-group species, such as diborenes,29 cationic boryl and borylene complexes,30–33 and iminoboryl, oxoboryl, and alkylideneboryl complexes;34–38 and (ii) is now well-established as a strong and synthetically-convenient transition metal Lewis base.39–46
Results and discussion
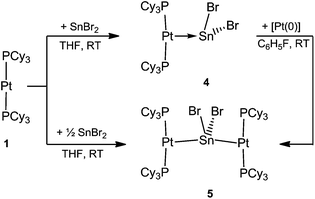
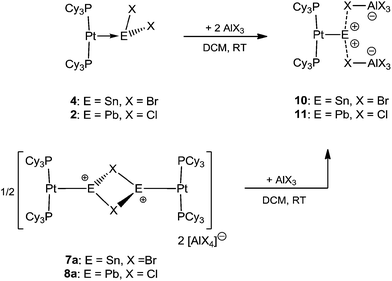
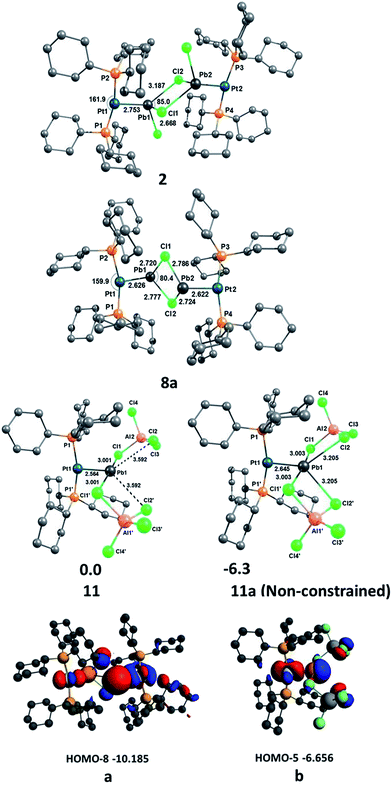
As part of our recent work to delineate the concept of metal-only Lewis Pairs (MOLPs),39–46 we recently reported the mono- and diplatinum plumbylene complexes [(Cy3P)2Pt–PbCl2]2 (2) and [{(Cy3P)2Pt}2PbCl2] (3).47 By qualitative inspection of the calculated frontier orbitals of these complexes, we had surmised the existence of σ donation both from Pt to Pb and from Pb to Pt, a phenomenon we described as synergic σ-donation.47 Subsequent DFT calculations indicated that similar bonding patterns exist in transition metal complexes containing multiple bonds between Group 10/14 elements.48 The qualitative EDA calculations done in this work, however, call this description into question (vide infra).In order to synthesize the analogous stannylene complex, we reacted stoichiometric amounts of tin(II) bromide with 1, which resulted in the formation of [(Cy3P)2Pt–SnBr2] (4) in near-quantitative yields. Likewise, the diplatinum species [{(Cy3P)2Pt}2SnBr2] (5) can be readily synthesized by addition of two equivalents of 1 to SnBr2 (Scheme 2).
The progress of the reactions was indicated by their color change from colorless (1) to violet-red (4) and purple-red (5), respectively. The 31P{1H} NMR spectra of the complexes revealed sharp singlets at δ = 49.7 ppm (1JP–Pt = 3421 Hz) for 4 and at δ = 50.7 ppm (1JP–Pt = 4197 Hz) for 5, which are slightly upfield-shifted in comparison to that of 1 (δ = 62.3 ppm, 1JP–Pt = 4164 Hz). All attempts to detect 119Sn{1H} NMR resonances failed, presumably due to an increased electric field gradient and large chemical shift anisotropy at the 119Sn site.49,50 The 195Pt{1H} NMR spectrum of 4 and 5 reveal triplets at δ = −4903 ppm (1JP–Pt = 3421 Hz) and at δ = −5239 ppm (1JP–Pt = 4197 Hz), respectively. The frequencies of the resonances and the change in the coupling constants is in accordance with those of previously reported plumbylene analogues.47
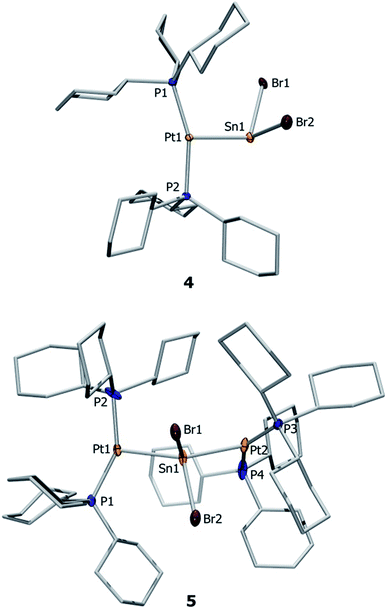
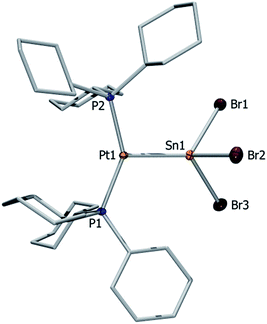
Both complexes 4 and 5 exhibit T-shaped geometry around the platinum center (Fig. 1). In contrast to the heavier lead analogue 2, compound 4 is not dimeric. The metal–metal distances dMM are compared with the sum of the experimentally derived radii of the atoms involved, ∑covrad, as sourced from a survey of the Cambridge Crystallographic Database. The resulting ratio, a useful tool for comparison of different dative bond lengths, is denoted drel.46 The Pt–Sn distances of the monoplatinum complex 4 (Pt1–Sn1 2.605(1) Å, drel = 0.947) and the diplatinum complex 5 (Pt1–Sn1 2.643(1) Å, drel = 0.961; Pt2–Sn1 2.657(1) Å, drel = 0.966) are very similar, and very similar drel values have been observed in the heavier lead analogues (2: drel = 0.968, 3: drel = 0.981, 0.989) and other known tin(II) halide-bridged transition metal complexes e.g. [{(Me3P)3ClRh}2(μ-SnCl2)] (6) (drel = 0.965, 0.968).47,51 The Pt–Sn–Pt angle of 5 (139.0(1)°) matches well with the diplatinum Pb complex 3 (140.1(1)°) and Marder's dirhodium species (142.5(1)°).51 Characteristic NMR and structural data for the neutral and cationic stannylene and plumbylene complexes are summarized in Table 1.
| Substance | 31P{1H}a | 1 J P–Pt | Pt–Mc | M–Xc |
|---|---|---|---|---|
| a δ in ppm. b Coupling constants in Hz. c Distances in Å. | ||||
| [(Cy3P)2Pt(PbCl2)] (2)47 | 48.3 | 3450 | 2.730(1) | 2.619(1), 3.139(1) |
| [{(Cy3P)2Pt}2PbCl2] (3)47 | 50.4 | 4032 | 2.767(1), 2.789(1) | 2.628(1), 2.616(1) |
| [(Cy3P)2Pt(SnBr2)] (4) | 49.7 | 3421 | 2.605(2) | 2.654(1), 2.626(2) |
| [{(Cy3P)2Pt}2SnBr2] (5) | 50.7 | 4197 | 2.643(1), 2.657(1) | 2.674(1), 2.661(1) |
| [(Cy3P)2Pt(SnBr)][AlBr4] (7a) | 49.9 | 3130 | ||
| [(Cy3P)2Pt(SnBr)][BArCl4] (7b) | 49.4 | 3104 | 2.524(1) | 2.780(1), 2.821(1) |
| [(Cy3P)2Pt(PbCl)][AlCl4] (8a) | 46.6 | 3099 | 2.603(1) | 2.769(3), 2.822(3) |
| [(Cy3P)2Pt(PbCl)][BArCl4] (8b) | 46.7 | 3115 | ||
| [(Cy3P)2Pt(Sn)][AlBr4]2 (10) | 52.1 | 3021 | 2.502(1) | 3.155(1), 3.264(1), 2.956(1) |
| [(Cy3P)2Pt(Pb)][AlCl4]2 (11) | 47.5 | 2950 | 2.564(1) | |
| [N(nBu)4][(Cy3P)2Pt(SnBr3)] (16) | 56.5 | 4634 | 2.604(1) | |
| [(Cy3P)2Pt(PbCl)(4-Me-C5H4N)][AlCl4] (17) | 47.1 | 3350 | ||
| [(Cy3P)2Pt(PbI)][AlCl4] (18) | 45.5 | 3130 | 2.619(1) | 2.917(2), 3.092(2) |
| [(Cy3P)2Pt(PbClBr)] (19) | 48.2 | 3520 | ||
Synthesis of low-valent Sn and Pb monocations
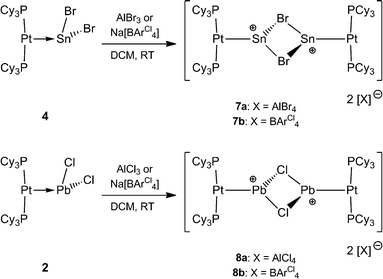
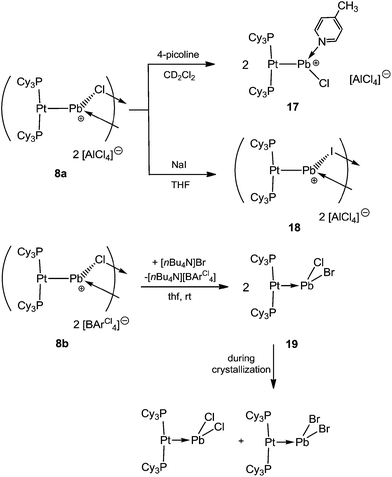
It was envisaged that divalent group 14 MOLPs may act as ideal precursors for the synthesis of low-coordinate group 14 cations, via halide abstraction. Stoichiometric addition of AlBr3 or Na[BArCl4] [ArCl = 3,5-Cl2-C6H3] to monoplatinum stannylene complex 4 and plumbylene complex 2 resulted in new cationic complexes [(Cy3P)2Pt(SnBr)]2[X]2 (7a = AlBr4, 7b = BArCl4), and [(Cy3P)2Pt–PbCl]2[X]2 (8a = AlBr4, 8b = BArCl4) (Scheme 3). In order to prevent halogen exchange between the MOLPs and aluminium halides, AlBr3 was chosen as halide abstracting agent for bromostannylene 4, and AlCl3 for the chloroplumbylene 2.All of these cations were characterized by multinuclear NMR spectroscopy and X-ray structural analysis. For all complexes, the 31P{1H} NMR spectrum shows a sharp singlet flanked by 195Pt satellites (7a: δ = 49.3 ppm, 1JP–Pt = 3097 Hz; 7b: δ = 49.4 ppm, 1JP–Pt = 3104 Hz; 8a: δ = 46.6 ppm, 1JP–Pt = 3100 Hz; 8b: δ = 46.7 ppm, 1JP–Pt = 3115 Hz). In comparison to the precursor there is almost no change of the chemical shift value (4: δ = 49.6 ppm, 1JP–Pt = 3421 Hz; 2: δ = 48.3 ppm, 1JP–Pt = 3450 Hz). However, the decrease of the 31P–195Pt coupling constants is a strong indicator of the formation of cationic complexes, as similar decreases were observed during the formation of platinum-boryl cations of the form trans-[(Cy3P)2Pt(MeCN){BBr(NMe2)}][BArF4] (9).52 The 27Al NMR spectrum reveals a broad singlet at δ = 80.8 ppm which is quite common for a tetrahedral aluminate.53 All attempts to detect 119Sn{1H}, 207Pb{1H}, or 195Pt{1H} NMR resonances of 7a,b and 8a,b (and, in fact, all of the complexes prepared herein) failed despite the use of wide spectral widths. This is presumably due to increased electric field gradient and large chemical shift anisotropy at the heavy tetrel element site, in addition to the extensive coupling with other NMR-active nuclei.49,50,54,55 This is in line with the well-documented difficulties in detecting 11B NMR signals in related cationic borylene complexes of the form [(Cy3P)2Pt(BRLn)]+ (n = 0, 1).30,32,33,52
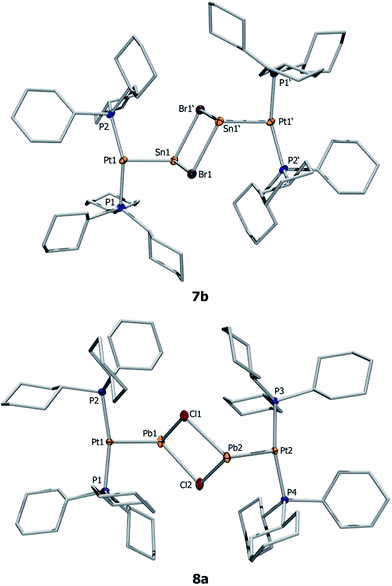
Orange crystals of 7a/b were grown by diffusion of hexanes into a CH2Cl2 solution at −40 °C and were analyzed by single-crystal X-ray diffraction. As the dication of 7a is centrosymmetric and the dications of 7a/b are identical, only the structural features of 7b are discussed here. Complex 7b features a slightly distorted T-shaped geometry around the platinum atom (Fig. 2). In the solid-state structure, the borate anion and tin cation are clearly separated, the shortest Sn⋯Cl(WCA) distance being 4.020(1) Å (WCA = weakly coordinating anion). This is not only longer than the longest Sn⋯Cl(WCA) distance in C (3.527 Å), but also than the sum of their van der Waals radii (3.92 Å).56 The Pt–Sn distances in 7b (2.524(2) Å) are significantly shorter than that of the starting material (4: 2.605(2) Å).
The X-ray-derived structural features of 8a are discussed here and the structural features of 8b are provided in the ESI.† Complex 8a crystallizes in the orthorhombic space group Pca21 (Fig. 2). In the solid-state structure of 8a, the tetrachloroaluminate anion and lead atoms are loosely associated, the shortest Pb⋯Cl(WCA) distance being 3.420(1) Å, which is much shorter than the sum of their van der Waals radii (3.77 Å).56 This long contact is in contrast to 7a, the cation of which shows complete separation from its WCA ([BArCl4]−). The complex features a slightly distorted T-shaped geometry around the platinum atom. As in the previous case, the Pt–Pb bonds (2.603(1) Å) are shorter than those of the precursor (2: 2.730(1) Å).
Synthesis of low-valent Sn and Pb dications
Naked divalent dications of tetrel elements are presumably far too unstable to be isolated. However, we reasoned that abstraction of two chlorides from 2 or 4 may provide simple, monocoordinate, low-valent Sn or Pb dications if the strongly Lewis basic nature of the metal center can be harnessed to partly relieve the electron deficiency of such a dication. The greater extent of Pt–M (M = Sn, Pb) σ donation in 7a and 8a over that in 4 and 2 might provide enough electronic stabilization to attenuate the reactivity of the M dication and allow its isolation. Addition of two equivalents of AlBr3 to 4 and AlCl3 to 2 resulted in the formation of the loosely-associated salts [(Cy3P)2Pt(Sn)][AlBr4]2 (10) and [(Cy3P)2Pt(Pb)][AlCl4]2 (11) (Scheme 4). Alternatively, halide abstraction from 7a and 8a using stoichiometric amounts of AlBr3 or AlCl3 also led to the desired dicationic species 10 and 11, respectively.The 31P{1H} NMR spectrum of compound 10 reveals a sharp singlet with 195Pt satellites at δ = 52.9 ppm (1JP–Pt = 2993 Hz), marginally downfield from that of 4 (δ = 49.7 ppm, 1JP–Pt = 3421 Hz). In contrast to 10, the low-valent Pb dicationic complex 11 exhibits a resonance (δ = 47.5 ppm, 1JP–Pt = 2950 Hz) marginally upfield of that of 2. However, the decrease of the coupling constants from the neutral species as well as from 7a/8a indicates the formation of a dicationic species. The 27Al NMR spectra of 10 and 11 reveal broad singlets at δ = 80.8 and 103.6 ppm, respectively, indicating a tetrahedral aluminate.53 No 119Sn{1H} or 207Pb{1H} NMR resonances were detected despite several attempts.
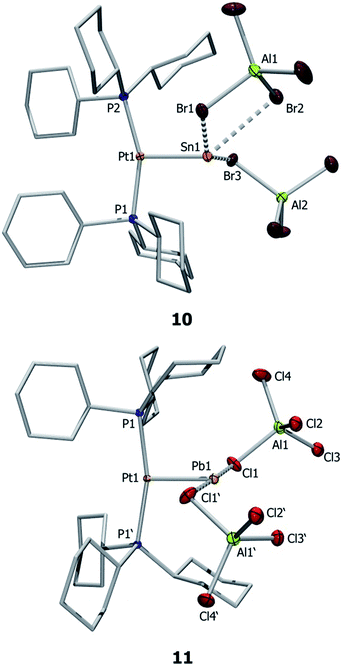
Single crystal X-ray diffraction studies of complex 10 confirmed the distorted T-shaped geometry around its platinum centre (Fig. 3) – a common feature of MOLPs involving [PtL2] Lewis bases.39–46 The Pt–Sn bond of this dicationic complex is even shorter than that of the monocationic complex (10: 2.502(1) Å; 7b: 2.524(1) Å). The tin center is weakly coordinated by three bromide atoms of two aluminate counteranions, with a Sn⋯Br(WCA)avg distance of 3.055(5) Å, markedly shorter than the sum of their van der Waals radii (4.0 Å).56 The shortest Sn–Br distance in 10 (2.956(1) Å) is significantly longer than regular Sn–Br bond lengths (ca. 2.59 Å).57 The published arene-stabilized, chlorine-bridged tin monocations [η6-(C6H6)2SnCl(AlCl4)]2 (12),58 and [η6-(C6Me6)SnCl(AlCl4)]4 (13)59 also possess bonds that are shorter than sum of their van der Waals radii (3.496(2) Å vs. 3.92 Å).56,57
Similar structural features are also observed in the case of 11 (Fig. 3), which exhibits a distorted T-shaped geometry around its platinum centre. The Pt–Pb bond length of 11 (2.564(1) Å) is 0.04 Å shorter than that in 8a and is shorter than typical Pt–Pb bonds. For example, the Pt–Pb distances in the metallocryptate [Pt2(P2phen)3Pb][ClO4]2 are 2.747(1) and 2.733(1) Å, indicating an attractive metallophilic interaction rather than Lewis acid–base interactions.26 The Pt–Pb distance in the complex [(AcO)Pb(crown-P2)Pt(CN)2][(O2CCH3)] (H) (3.313(2) Å) is long enough to raise questions about the existence of bonding between these two entities.27 Another Pt–Pb compound, [nBu4N]2[{Pt(C6F5)4}2(Pb)] (I), shows interactions between the Pb center and the endo fluorine atoms.28 The Pb center in 11 also exhibits weak interactions with two aluminate anions (Pb⋯Cl(WCA)avg 3.001(1) Å), leading to a pseudo-T-shaped geometry at the Pb atom.56 We cannot disregard two additional Pb⋯Cl interactions with the [AlCl4]− anions (3.592(1) Å), which although long are nevertheless shorter than the sum of the van der Waals radii (3.77 Å).56 Our calculations also showed that these interactions persist even in the gas phase, provided non-constrained calculations were used. The Pb⋯Cl interaction is considerably shorter than those in 8a (3.420(1) Å) but significantly longer than the Pb–Cl single bond length (2.300(4) Å) reported for LPbCl [L = HC(CMeNAr)2 (Ar = 2,6-iPr2C6H3)] (14).60 The distance is in the same range as other weak Pb⋯Cl interactions, e.g. in the arene-stabilized lead(II) dications [(1,2-C6H4Me2)2Pb (AlCl4)2] (F) (2.969(1) Å) or [(C6H6)2Pb][AlCl4]2 (15) (2.854(8)–3.218(9) Å).20,22
We subsequently attempted exchange of the donor fragment [(Cy3P)2Pt] from the dication 11. Upon addition of aromatic donor ligands (benzene and fluorobenzene), no exchange reaction was observed. Likewise, no exchange was observed upon addition of the strong N-donor ligand DMAP.
Synthesis of a stannyl anion
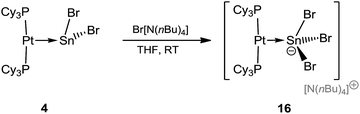
After the isolation of low-valent tin mono- and dications by halide abstraction from 4, we sought to conversely add another halide to form anionic tin compounds. The preparation of the anionic species [NnBu4][(Cy3P)2Pt(SnBr3)] (16) is shown in Scheme 5.The stoichiometric addition of [NnBu4]Br to 4 resulted in the formation of an anionic complex containing a formal Pt–Sn dative bond, along with a tetrabutylammonium countercation, [NnBu4][(Cy3P)2Pt(SnBr3)] (16), in good yields (80%). Such additions of bromide anions to tin(II) compounds, yielding anionic tin(II) salts, are known in cases where the tin atom is ligated by main group donors, but are unknown in cases where the Lewis base is a transition metal fragment.61,62 The 31P{1H} NMR spectra of 16 reveals a sharp singlet at δ = 56.2 ppm (1JP–Pt = 4634 Hz), slightly upfield in comparison to that of precursor 4δ = 49.7 ppm (1JP–Pt = 3421 Hz), while the coupling constant increased by ∼1200 Hz, indicating a significantly modified chemical environment around the Sn atom. As in previous cases, all attempts to detect 119Sn{1H} NMR resonances failed.49,50
Red crystals of 16 were analyzed by single-crystal X-ray diffraction (Fig. 4), displaying a Pt–Sn distance (2.604(1) Å) nearly identical to that of its precursor (2.605(2) Å). As expected, the Sn atom is strongly pyramidalized. The average Sn–Br distance in the stannyl anion (2.69 Å) is longer than the average Sn–Br distance (2.63 Å) in 4, presumably due to the introduction of another Br, which increases the steric demand at the Sn center.
Reactivity of low-valent Pb cations
Cationic species are known to form adducts with Lewis bases,3 prompting us to study the reaction of 8a with 4-picoline. This reaction afforded the 4-picoline-coordinated low-valent Pb cation [{(Cy3P)2Pt}PbCl(4-pic)][AlCl4] (17) (Scheme 6). Although all attempts to grow X-ray quality single crystals for diffraction analysis failed, the formation of 17 was clearly demonstrated from its 31P{1H} NMR spectrum (17: δ = 47.1 ppm; 1JP–Pt = 3370 Hz), which showed an increase of the coupling constant with respect to that of the starting material (8a: δ = 46.6 (1JP–Pt = 3100 Hz) ppm). Additionally, we were able to see the respective picoline resonances, with appropriate integration, in the 1H and 13C{1H} NMR spectra, slightly shifted with respect to free picoline.To further investigate the reactivity of our cationic plumbylene complexes we attempted halide exchange reactions. Addition of NaI to a THF solution of 8a led to a halide exchange reaction at the Pb atoms and isolation of the new dinuclear dicationic complex [(Cy3P)2Pt(PbI)]2[AlCl4]2 (18) (Scheme 6). The 31P{1H} NMR spectrum of 18 reveals a sharp singlet at δ = 45.5 ppm (1JP–Pt = 3130 Hz). Single crystal X-ray determination showed the same constitution as compound 8a. The Pt–Pb and Pb–I bond lengths in 18 are 2.61(1) Å and 2.917(1)/3.092(1) Å, respectively (see ESI†). All bond lengths are slightly elongated with respect to the chloro precursor 8a, as expected due to the larger covalent radius of iodide.56
In contrast to 8a, the reaction between 8b and [NnBu4]Br in THF resulted in a MOLP containing a lead atom with mixed halogens [(Cy3P)2Pt–PbClBr] (19) instead of a putative halogen exchange product (Scheme 6). Despite the absence of structural evidence, the formation of 19 was apparent from the 31P{1H} and 195Pt{1H} NMR spectra, which show a singlet at δ = 48.6 ppm (1JP–Pt = 3520 Hz) and a triplet at δ = −3950 ppm, respectively. These data show very little difference to those of the dichloro analogue 2 (31P: δ = 48.3 (1JPt–P = 3450 Hz) ppm, 195Pt: δ = −4025 ppm). During crystallization from toluene, a disproportionative halide exchange takes place, leading to the formation of two neutral species, [(Cy3P)2Pt–PbX2] (X = Cl, Br), which were confirmed by X-ray structure analysis as well as by 31P{1H} NMR spectroscopy. This serendipitous finding serves as further evidence for the formation of complex 19.
DFT calculations on the PtPb complexes 2, 8a and 11
In order to gain a deeper understanding of the bonding situation in the PtPb complexes 2, 8a and 11, quantum chemical calculations were carried out at the RI-D3(BJ)-BP86 level using def2-TZVP for the non-metal atoms and def2-QZVP for the Pt and Pb atoms.63–67 The optimized geometries of the complexes are shown in Fig. 5, including the most important bond lengths and bond angles. The calculated bond lengths agree well with the experimental bond lengths when the intermolecular dispersion interactions, and especially the damping factor (BJ), have been taken into account, as its importance has been previously reported by Grimme.68 A constrained geometry optimization was performed for 11 to further analyze the Pt–Pb bond because its non-constrained optimization converged to a structure in which two chloride atoms Cl2 and Cl2′ are bound to Pb1 (11a, Fig. 5). This is presumably a result of the absence of crystal packing effects, as the chloride atoms are presumably stabilized by the dielectric field created by the positively charged protons on the cyclohexyl groups of the surrounding molecules. We discuss the interaction of Cl2 and Cl2′ with Pb1 in detail in the bond analysis section below.NBO analysis69 shows that the Pt atom always carries a negative charge in these complexes (−0.483, −0.420 and −0.485e in 2, 8a and 11, respectively), which means there is a significant charge donation from the ligands to Pt, especially from the strong PCy3 donor ligands. However, the partial charges of the Pb atoms are always positive (1.174, 1.124 and 1.070e in 2, 8a and 11, respectively), and remain relatively constant upon successive halide abstraction and increase of net positive charge. This suggests that build-up of positive charge created by the removal of halides from Pb is effectively compensated by the connected groups, which, given the relatively constant charge on Pt, presumably stems from the short contacts with nearby halides.
We investigated the nature of the Pt–Pb bonding in the complexes 2, 8a and 11 with an energy decomposition analysis (EDA-NOCV)70 using two different fragmentation patterns, D and E. D describes donor–acceptor interactions whereas E describes an electron sharing bonding scheme between the Pt and Pb fragments. The EDA-NOCV data given in Table 2 suggest that the Pt–Pb bond in 2 is dative in nature, whereas those of 8a and 11 are electron-sharing bonds. The ΔEorb value of 2 in model D (−65.7 kcal mol−1), where both the singlet state of [(Cy3P)2Pt] and [PbCl2–PbCl2–Pt(PCy3)2] were used as interacting fragments, has a weaker interaction than model E (ΔEorb = −117.7 kcal mol−1), where doublet states of [(Cy3P)2Pt]+ and [PbCl2–PbCl2–Pt(PCy3)2]− were used as interacting fragments. Here we applied the rule that the best description of a chemical bond comes from the interacting fragments that give the weakest orbital interaction (ΔEorb), as suggested by Frenking based on his work on carbodiphosphoranes in which the same charge and spin states of the fragments were compared,71 in addition to his other work in which different charge and spin states of the fragments were compared for the analysis of M–E (M = Fe, Ru, Os; E = C–Sn)72 and E–C bonds (E = Be, B+, C2+, N3+, O4+).73 The ΔEorb values of 8a (−107.3 kcal mol−1) and 11 (−117.4 kcal mol−1) in model E are significantly lower than those of 8a (−127.5 kcal mol−1) and 11 (−131.4 kcal mol−1) in model D. Therefore, the Pt–Pb bonds in 8a and 11 are electron-sharing in nature, whereas that of 2 is a dative bond. This difference in bonding upon halide abstraction suggests that the electron pair donated by Pt to Pb in 2 is converted to a fully-covalent bonding σ orbital in 8a and 11. The analysis of the Kohn–Sham molecular orbitals reveals that the HOMO-8 of 8a (a, Fig. 5) and HOMO-5 of 11 (b, Fig. 5) both exhibit σ orbitals formed from a d orbital of Pt and a p orbital of Pb.
| Compound | 2 | 2 | 8a | 8a | 11 | 11 |
|---|---|---|---|---|---|---|
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEdisp + ΔEorb. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. c D: donor–acceptor bonding model; E: electron sharing bonding model. | ||||||
| Fragmentation pattern | Dc | Ec | Dc | Ec | Dc | Ec |
| Fragment 1 | [(Cy3P)2Pt] | [Cy3P]2Pt+ | [(Cy3P)2Pt] | [(Cy3P)2Pt]+ | [(Cy3P)2Pt] | [(Cy3P)2Pt]+ |
| Fragment 2 | [PbCl2–PbCl2–Pt(PCy3)2] | [PbCl2–PbCl2–Pt(PCy3)2]− | [PbCl–PbCl–Pt(PCy3)2]2+ | [PbCl–PbCl–Pt(PCy3)2]+ | [Cl4Al–Pb–AlCl4] | [Cl4Al–Pb–AlCl4]− |
| ΔEint | −68.3 | −176.0 | −128.1 | −77.1 | −120.5 | −163.9 |
| ΔEPauli | 146.9 | 169.5 | 173.7 | 192.9 | 200.5 | 249.7 |
| ΔEelstata | −104.7 (48.7%) | −183.1 (53.0%) | −124.2 (41.2%) | −112.7 (41.7%) | −139.9 (43.6%) | −246.5 (59.6%) |
| ΔEdispa | −44.7 (20.8%) | −44.7 (12.9%) | −50.1 (16.6%) | −50.1 (18.5%) | −49.8 (15.5%) | −49.8 (12.0%) |
| ΔEorba | −65.7 (30.5%) | −117.7 (34.1%) | −127.5 (42.2%) | −107.3 (39.7%) | −131.4 (40.9%) | −117.4 (28.4%) |
| ΔEσb Pt → Pb | −32.6 (49.6%) | — | −65.1 (51.1%) | — | −60.2 (45.8%) | — |
| ΔEσb Pt–Pb | — | −87.2 (74.1%) | — | −67.5 (62.9%) | — | −70.1 (59.7%) |
| ΔEπ‖b Pt → Pb | −7.1 (10.8%) | −2.4 (2.0%) | −9.7 (7.6%) | −10.6 (9.9%) | −9.7 (7.4%) | −17.2 (14.7%) |
| ΔEπ⊥b Pt → Pb | −4.8 (7.3%) | −4.8 (4.1%) | −15.4 (12.1%) | −6.2 (5.8%) | −25.4 (19.3%) | −6.4 (5.5%) |
| ΔEσb Pb → Pt | −3.8 (5.8%) | — | −5.3 (4.2%) | — | −4.0 (3.0%) | — |
| Restb | −17.4 (26.5%) | −23.3 (19.8%) | −32.0 (25.0%) | −23.0 (21.4%) | −32.1 (24.5%) | −23.6 (20.2%) |
| ΔEprep | 12.9 | 5.1 | 37.5 | 17.3 | 52.9 | 12.3 |
| −De | −55.4 | −170.9 | −90.6 | −59.8 | −67.6 | −151.6 |
We have analyzed the Pb–Cl bonding in 2, 8a and 11 with the EDA-NOCV method using singlet [(Cy3P)2Pt–PbCl2] for 2, singlet [(Cy3P)2Pt–PbCl]+ for 8a and singlet [(Cy3P)2Pt–Pb]2+ and [AlCl4⋯AlCl4]2− for 11 as interacting fragments. The EDA-NOCV results (Table 3) show that the orbital (covalent) interactions ΔEorb are stronger (−67.7 kcal mol−1) than the electrostatic (ionic) interactions ΔEelstat (−48.7 kcal mol−1) in 8a. However, the electrostatic interactions are stronger in 2 (−43.0 kcal mol−1) and 11 (−257.6 kcal mol−1) than the corresponding orbital interactions in 2 (−26.6 kcal mol−1) and 11 (−69.9 kcal mol−1) (Table 3). The breakdown of ΔEorb into contributions from orbitals having different symmetry reveals that the dominant contribution comes from Cl → Pb σ-donation. The Pb → Cl σ backdonation is very weak for 8a (11.1%) and almost negligible for 2 (4.9%) and 11 (1.7%). The crystal structure of 11 shows two additional Pb1⋯Cl2 and Pb1⋯Cl2′ short contacts (3.592 Å) and non-constrained gas phase optimization (11a, Fig. 5) converged to a structure in which these short contacts strengthen (3.205 Å), the structure thereby becoming similar to the structure of [(1,2-C6H4Me2)2Pb][AlCl4]2 (F) reported by Frank et al.22 According to the EDA-NOCV method, the sum of the orbital interaction energies of the two Pb1⋯Cl2 and Pb1⋯Cl2′ contacts is very weak (11.9 kcal mol−1), indicating that each of these contacts has a roughly 6.0 kcal mol−1 orbital interaction energy. These two chloride atoms in the crystal are presumably stabilized by the positively charged protons on the cyclohexyl groups of the surrounding molecules. In the absence of crystal packing effects, Pb1⋯Cl2 and Pb1⋯Cl2′ interactions strengthen and the non-constrained gas phase optimized geometry 11a becomes similar to the aforementioned structure reported by Frank et al. The bond dissociation energies decrease to −4.7 kcal mol−1 for 2 and +25.3 kcal mol−1 for 8a without including dispersion energies, which shows the importance of introducing the dispersion interactions.68 It is clear that dispersion interactions have a strong effect on the thermodynamic stability of 2 and 8a, as mentioned in the analysis of the Pt–Pb bonds above, as was also pointed out by Power et al.74
| Compound | 2 | 8a | 11 |
|---|---|---|---|
| a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEdisp + ΔEorb. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. | |||
| Fragment 1 | [(Cy3P)2Pt–PbCl2] | [(Cy3P)2Pt–PbCl]+ | [(Cy3P)2Pt–Pb]2+ |
| Fragment 2 | [(Cy3P)2Pt–PbCl2] | [(Cy3P)2Pt–PbCl]+ | [AlCl4⋯AlCl4]2− |
| ΔEint | −40.5 | −29.9 | −290.2 |
| ΔEPauli | 61.1 | 129.7 | 76.3 |
| ΔEelstata | −43.0 (42.3%) | −48.7 (30.5%) | −257.6 (70.3%) |
| ΔEdispa | −32.0 (31.5%) | −43.2 (27.1%) | −39.1 (10.7%) |
| ΔEorba | −26.6 (26.2%) | −67.7 (42.4%) | −69.9 (19.0%) |
| ΔEσb Cl → Pb | −13.6 (51.1%) | −39.1 (57.8%) | −25.8 (36.9%) |
| ΔEσb Pb → Cl | −1.3 (4.9%) | −7.5 (11.1%) | 1.2 (1.7%) |
| ΔEπ⊥b Cl → Pb | −1.5 (5.6%) | −7.1 (10.5%) | 2.0 (2.9%) |
| ΔEσb (Cl2, Cl6) → Pb | — | — | −11.9 (17.0%) |
| Restb | −10.2 (38.3%) | −14.0 (20.7%) | −29.0 (41.5%) |
| ΔEprep | 3.8 | 12.0 | 50.4 |
| −De | −36.7 | −17.9 | −239.8 |
Conclusions
In this paper, we have sequentially abstracted halide ions from dihalostannylene and plumbylene complexes, leading first to dicationic dinuclear complexes and then to unprecedented low-valent dicationic complexes containing Pt–Sn and Pt–Pb bonds. The reactivity of a number of the neutral and cationic complexes with halide salts and Lewis bases was also probed. The EDA-NOCV data reveal that the Pt–Pb bond is electron-sharing in nature in 8a and 11, whereas it is a dative bond in 2. The EDA-NOCV data also reveal that the ionic interactions in Pt–Pb bond are always stronger than the covalent interactions in 2, 8a and 11. Ionic interactions also predominate in the Pb–Cl bonds of 2 and 11, but not 8a. The calculated D3 intramolecular dispersion energies in the analysis of Pt–Pb and Pb–Cl bonds indicate that dispersion forces have an important effect on the thermodynamic stability of 2, 8a and 11.Computational details
Geometry optimizations of the complexes were carried out at BP86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66 level using a mix basis set of def2-TZVP67 for nonmetals and def2-QZVP67 for Pt and Pb, as implemented in Turbomole 6.5.75 DFT-D3
66 level using a mix basis set of def2-TZVP67 for nonmetals and def2-QZVP67 for Pt and Pb, as implemented in Turbomole 6.5.75 DFT-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 64 was used to include van der Waals forces including the Becke–Johnson damping (BJ).65 The geometry optimizations were performed without geometry constraints for 2, 8a and 11a. However, a constrained geometry optimization has also been performed for 11 where P1, P1′, Pt1, Pb1, Cl1, Cl2, Cl4, Cl1′, Cl2′ and Cl4′ (Fig. 5) were frozen to their X-ray structure positions, as the non-constrained geometry optimization converged to a structure (11a) in which two chloride atoms were bound to the Pb1 atom. The NBO69 charges were calculated at the same level of theory. All complexes were characterized as minima by calculation of vibrational frequencies. The resolution-of-identity (RI)63 method was used for the calculations.
64 was used to include van der Waals forces including the Becke–Johnson damping (BJ).65 The geometry optimizations were performed without geometry constraints for 2, 8a and 11a. However, a constrained geometry optimization has also been performed for 11 where P1, P1′, Pt1, Pb1, Cl1, Cl2, Cl4, Cl1′, Cl2′ and Cl4′ (Fig. 5) were frozen to their X-ray structure positions, as the non-constrained geometry optimization converged to a structure (11a) in which two chloride atoms were bound to the Pb1 atom. The NBO69 charges were calculated at the same level of theory. All complexes were characterized as minima by calculation of vibrational frequencies. The resolution-of-identity (RI)63 method was used for the calculations.
The calculations for the energy decomposition analysis (EDA-NOCV)70 were carried out with the program package ADF 2013.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 at BP86 in conjunction with a triple-ζ-quality basis set TZ2P77 where relativistic effects are considered with the ZORA approximation.78 The RI-D3(BJ)-BP86/def2-TZVP + def2-QZVP optimized geometries were used for the EDA-NOCV calculations. The effect of dispersion interactions on EDA-NOCV were estimated using the D3 dispersion correction including BJ damping. This level of theory is denoted D3(BJ) + BP86/TZ2P//RI-D3(BJ)-BP86/def2-TZVP + def2-QZVP. In the EDA the bond dissociation energy, De, of a molecule (AB) is divided into the preparation energy ΔEprep and the intrinsic interaction energy ΔEint:
76 at BP86 in conjunction with a triple-ζ-quality basis set TZ2P77 where relativistic effects are considered with the ZORA approximation.78 The RI-D3(BJ)-BP86/def2-TZVP + def2-QZVP optimized geometries were used for the EDA-NOCV calculations. The effect of dispersion interactions on EDA-NOCV were estimated using the D3 dispersion correction including BJ damping. This level of theory is denoted D3(BJ) + BP86/TZ2P//RI-D3(BJ)-BP86/def2-TZVP + def2-QZVP. In the EDA the bond dissociation energy, De, of a molecule (AB) is divided into the preparation energy ΔEprep and the intrinsic interaction energy ΔEint:
| ΔE (= −De) = ΔEint + ΔEprep | (1) |
The intrinsic interaction energy ΔEint is further divided into four main components:
| ΔEint = ΔEelstat + ΔEdisp + ΔEPauli + ΔEorb | (2) |
The ΔEelstat parameter corresponds to the quasiclassical electrostatic interaction energy between the fragments calculated by means of the frozen electron density distribution of the fragments in the geometry of the molecules. ΔEdisp accounts for the intramolecular dispersion energy. ΔEPauli refers to the repulsive interactions between the fragments, which include destabilizing interactions between occupied orbitals and any steric repulsion. The stabilizing orbital interaction term ΔEorb is calculated in the final step of the energy partitioning analysis when the Kohn–Sham orbitals relax to their optimal form.
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft. SSS thanks the AvH foundation for a postdoctoral fellowship.Notes and references
- P. Jutzi, F. Kohl, P. Hofmann, C. Krueger and Y.-H. Tsay, Chem. Ber., 1980, 113, 757 CrossRef CAS.
- P. A. Rupar, V. N. Staroverov and K. M. Baines, Science, 2008, 322, 1360 CrossRef CAS PubMed.
- S. Khan, G. Gopakumar, W. Thiel and M. Alcarazo, Angew. Chem., Int. Ed., 2013, 52, 5644 CrossRef CAS PubMed.
- M. Driess, S. Yao, M. Brym and C. van Wullen, Angew. Chem., Int. Ed., 2006, 45, 6730 CrossRef CAS PubMed.
- B. Rhodes, J. C. W. Chien and M. D. Rausch, Organometallics, 1998, 17, 1931 CrossRef CAS.
- T. Probst, O. Steigelmann, J. Riede and H. Schmidbaur, Angew. Chem., Int. Ed. Engl., 1990, 29, 1397 CrossRef.
- J. Li, C. Schenk, F. Winter, H. Scherer, N. Trapp, A. Higelin, S. Keller, R. Pottgen, I. Krossing and C. Jones, Angew. Chem., Int. Ed., 2012, 51, 9557 CrossRef CAS PubMed.
- A. Schäfer, F. Winter, W. Saak, D. Haase, R. Pöttgen and T. Müller, Chem.–Eur. J., 2011, 17, 10979 CrossRef PubMed.
- T. Müller, Adv. Organomet. Chem., 2005, 53, 155 CrossRef.
- P. A. Rupar, V. N. Staroverov, P. J. Ragogna and K. M. Baines, J. Am. Chem. Soc., 2007, 129, 15138 CrossRef CAS PubMed.
- P. A. Rupar, R. Bandyopadhyay, B. F. T. Cooper, M. R. Stinchcombe, P. J. Ragogna, C. L. B. Macdonald and K. M. Baines, Angew. Chem., Int. Ed., 2009, 48, 5155 CrossRef CAS PubMed.
- F. Cheng, A. L. Hector, W. Levason, G. Reid, M. Webster and W. Zhang, Angew. Chem., Int. Ed., 2009, 48, 5152 CrossRef CAS PubMed.
- P. Jutzi, A. Mix, B. Rummel, W. W. Schoeller, B. Neumann and H. G. Stammler, Science, 2004, 305, 849 CrossRef CAS PubMed.
- P. Jutzi, R. Dickbreder and H. Nöth, Chem. Ber., 1989, 122, 865 CrossRef CAS.
- S. Hino, M. Brynda, A. D. Phillips and P. P. Power, Angew. Chem., Int. Ed., 2004, 43, 2655 CrossRef CAS.
- M. J. Taylor, A. J. Saunders, M. P. Coles and J. R. Fulton, Organometallics, 2011, 30, 1334 CrossRef CAS.
- A. M. Orlova, I. B. Sivaev, V. L. Lagun, S. B. Katser, K. A. Solntsev and N. T. Kuznetsov, Russ. J. Coord. Chem., 1996, 22, 110 CAS.
- J. M. Harrowfield, H. Miyamae, B. W. Skelton, A. A. Soudi and A. H. White, Aust. J. Chem., 2002, 55, 661 CrossRef CAS.
- M. Kadarkaraisamy, D. P. Engelhart, P. N. Basa and A. G. Sykes, J. Coord. Chem., 2010, 63, 2261 CrossRef CAS.
- A. G. Gash, P. F. Rodesiler and E. L. Amma, Inorg. Chem., 1974, 13, 2429 CrossRef CAS.
- V. N. Kokozay and A. V. Sienkiewicz, Polyhedron, 1995, 14, 1547 CrossRef CAS.
- W. Frank and F. G. Wittmer, Chem. Ber., 1997, 130, 1731 CrossRef CAS.
- A. C. Filippou, P. Portius and A. I. Philippopoulos, Organometallics, 2002, 21, 653 CrossRef CAS.
- A. C. Filippou, A. I. Philippopoulos and G. Schnakenburg, Organometallics, 2003, 22, 3339 CrossRef CAS.
- A. C. Filippou, A. I. Philippopoulos, P. Portius and G. Schnakenburg, Organometallics, 2004, 23, 4503 CrossRef CAS.
- V. J. Catalano, B. L. Bennett and B. C. Noll, Chem. Commun., 2000, 1413 RSC.
- A. L. Balch, E. Y. Fung, J. K. Nagle, M. M. Olmstead and S. P. Rowley, Inorg. Chem., 1993, 32, 3295 CrossRef CAS.
- R. Uson, J. Fornies, L. R. Falvello, M. A. Uson and I. Uson, Inorg. Chem., 1992, 31, 3697 CrossRef CAS.
- H. Braunschweig, A. Damme, R. D. Dewhurst and A. Vargas, Nat. Chem., 2013, 5, 115 CrossRef CAS PubMed.
- H. Braunschweig, K. Radacki and K. Uttinger, Angew. Chem., Int. Ed., 2007, 46, 3979 CrossRef CAS PubMed.
- H. Braunschweig, K. Radacki, D. Rais and D. Scheschkewitz, Angew. Chem., Int. Ed., 2005, 44, 5651 CrossRef CAS PubMed.
- H. Braunschweig, K. Radacki and K. Uttinger, Organometallics, 2008, 27, 6005 CrossRef CAS.
- H. Braunschweig, P. Brenner, R. D. Dewhurst, J. O. C. Jimenez-Halla, T. Kupfer, D. Rais and K. Uttinger, Angew. Chem., Int. Ed., 2013, 52, 2981 CrossRef CAS PubMed.
- H. Braunschweig, K. Radacki, D. Rais and K. Uttinger, Angew. Chem., Int. Ed., 2006, 45, 162 CrossRef CAS PubMed.
- H. Braunschweig, T. Kupfer, K. Radacki, A. Schneider, F. Seeler, K. Uttinger and H. Wu, J. Am. Chem. Soc., 2008, 130, 7974 CrossRef CAS PubMed.
- H. Braunschweig, K. Radacki and A. Schneider, Science, 2010, 328, 345 CrossRef CAS PubMed.
- J. Brand, H. Braunschweig and S. S. Sen, Acc. Chem. Res., 2014, 47, 180 CrossRef CAS PubMed.
- J. Brand, H. Braunschweig, F. Hupp, A. K. Phukan, K. Radacki and S. S. Sen, Angew. Chem., Int. Ed., 2014, 53, 2240 CrossRef CAS PubMed.
- H. Braunschweig, K. Gruss and K. Radacki, Angew. Chem., Int. Ed., 2009, 48, 4239 CrossRef CAS PubMed.
- H. Braunschweig, K. Gruss and K. Radacki, Angew. Chem., Int. Ed., 2007, 46, 7782 CrossRef CAS PubMed.
- H. Braunschweig, K. Gruss and K. Radacki, Inorg. Chem., 2008, 47, 8595 CrossRef CAS PubMed.
- H. Braunschweig, P. Brenner, P. Cogswell, K. Kraft and K. Schwab, Chem. Commun., 2010, 46, 7894 RSC.
- H. Braunschweig, K. Radacki and K. Schwab, Chem. Commun., 2010, 46, 913 RSC.
- H. Braunschweig, P. Cogswell and K. Schwab, Coord. Chem. Rev., 2011, 255, 101 CrossRef CAS PubMed.
- J. Bauer, H. Braunschweig, P. Brenner, K. Kraft, K. Radacki and K. Schwab, Chem.–Eur. J., 2010, 16, 11985 CrossRef CAS PubMed.
- J. Bauer, H. Braunschweig and R. D. Dewhurst, Chem. Rev., 2012, 112, 4329 CrossRef CAS PubMed.
- H. Braunschweig, A. Damme, R. D. Dewhurst, F. Hupp, J. O. C. Jimenez-Halla and K. Radacki, Chem. Commun., 2012, 48, 10410 RSC.
- W. H. Liao, P. Y. Ho and M. D. Su, Inorg. Chem., 2013, 52, 1338 CrossRef CAS PubMed.
- R. R. Sharp, J. Chem. Phys., 1972, 57, 5321 CrossRef CAS PubMed.
- R. R. Sharp and J. W. Tolan, J. Chem. Phys., 1976, 65, 522 CrossRef CAS PubMed.
- D. M. Chan and T. B. Marder, Angew. Chem., Int. Ed., 1988, 27, 442 CrossRef.
- N. Arnold, H. Braunschweig, P. Brenner, J. O. C. Jimenez-Halla, T. Kupfer and K. Radacki, Organometallics, 2012, 31, 1897 CrossRef CAS.
- Z. Cerny, J. Machacek, J. Fusek, B. Casensky, O. Kriz and D. G. Tuck, J. Chem. Soc., Dalton Trans., 1998, 1439 RSC.
- R. M. Hawk and R. R. Sharp, J. Chem. Phys., 1974, 60, 1009 CrossRef CAS PubMed.
- R. M. Hawk and R. R. Sharp, J. Chem. Phys., 1974, 60, 1522 CrossRef CAS PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806 CrossRef CAS PubMed.
- B. Cordero, V. Gomez, A. E. Platero-Prats, M. Reves, J. Echeverria, E. Cremades, F. Barragan and S. Alvarez, Dalton Trans., 2008, 2832 RSC.
- H. Schmidbaur, T. Probst, B. Huber, O. Steigelmann and G. Müller, Organometallics, 1989, 8, 1567 CrossRef CAS.
- H. Schmidbaur, T. Probst, B. Huber, G. Müller and C. Krueger, J. Organomet. Chem., 1989, 365, 53 CrossRef CAS.
- A. Jana, S. P. Sarish, H. W. Roesky, C. Schulzke, A. Doering and M. John, Organometallics, 2009, 28, 2563 CrossRef CAS.
- D. Weber, S. H. Hausner, A. Eisengraeber-Pabst, S. Yun, J. A. Krause-Bauer and H. Zimmer, Inorg. Chim. Acta, 2004, 357, 125 CrossRef CAS.
- S. Baba Haj, M. Schuermann, L. Iovkova-Berends, S. Herres-Pawlis and K. Jurkschat, Organometallics, 2012, 31, 4716 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Ohm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 242, 652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- D. Heitmann, T. Pape, A. Hepp, C. Mück-Lichtenfeld, S. Grimme and F. E. Hahn, J. Am. Chem. Soc., 2011, 133, 11118 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- (a) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962 CrossRef CAS; (b) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- R. Tonner and G. Frenking, Chem.–Eur. J., 2008, 14, 3260 CrossRef CAS PubMed.
- P. Parameswaran and G. Frenking, Chem.–Eur. J., 2009, 15, 8807 CrossRef CAS PubMed.
- M. A. Celik, G. Frenking, B. Neumüller and W. Petz, ChemPlusChem, 2013, 78, 1024 CrossRef CAS.
- C.-Y. Lin, J.-D. Guo, J. C. Fettinger, S. Nagase, F. Grandjean, G. J. Long, N. F. Chilton and P. P. Power, Inorg. Chem., 2013, 52, 13584 CrossRef CAS PubMed.
- TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, Karlsruhe, 2013, http://www.turbomole.com.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- J. G. Snijders, E. J. Baerends and P. Vernoojs, At. Data Nucl. Data Tables, 1982, 26, 483 CrossRef.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and synthetic procedures, characterisation data, computational details, and crystallographic methods employed in this work are given. CCDC 1002025–1002028 and 1023363–1023368. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc02948h |
| This journal is © The Royal Society of Chemistry 2015 |