Relationship between negative thermal expansion and lattice dynamics in a tetragonal PbTiO₃–Bi(Mg_1/2Ti_1/2)O₃ perovskite single crystal

Abstract

A range of compelling information on the thermal expansion behavior and lattice dynamics of a novel ferroelectric perovskite-type 0.62PbTiO₃–0.38Bi(Mg_1/2Ti_1/2)O₃ single crystal has been revealed by means of temperature-dependent X-ray diffraction and polarized Raman scattering. X-ray diffraction analysis suggests a strong ferroelectricity and structural change (tetragonal to cubic) upon heating. The A₁(1TO) soft mode, associated with the order parameter spontaneous polarization displacement, abnormally shifts downward and vanished, indicating the change in polar nanoregions and phase transition. Both the temperature dependent unit cell volume and frequency of the soft mode confirm the correlation between spontaneous polarization and negative thermal expansion. The experimental evidence of spontaneous volume ferroelectrostriction will further help in understanding the relationship between the structure and optical properties of perovskite-type ferroelectric oxides.

---

1 Introduction

In recent years, complex mixed-ion ferroelectric materials have been extensively investigated in order to achieve optimum properties as well as to understand the underlying factors for property tweaking.^1–4 PbTiO₃ (PT)-based perovskite compounds are important multifunctional materials, which have been investigated in the last half century due to their controllable physical properties, such as ferroelectric, piezoelectric, optical, and electric properties.^5–8 Most recently, the research hotspot of PbTiO₃–BiMeO₃ ferroelectrics, where Me can be a single cation of valency +3 (e.g. Sc³⁺, In³⁺ and Fe³⁺)^9–14 or a mixture of cations with an average valence of +3 (e.g. Zn_1/2Ti_1/2, Mg_1/2Ti_1/2, and Ni_1/2Ti_1/2),^6,15–18 have stimulated much interest. Their excellent optoelectronic/piezoelectric properties and high Curie temperature (T_C) are the key parameters in piezoelectric devices for applications with a stable structure and performance under specific temperature conditions.

A significant alternative system of PbTiO₃–BiMeO₃ is involved in PbTiO₃–Bi(Mg_1/2Ti_1/2)O₃ (PT–BMT), which has being considerably studied due to its good performances such as high T_C, low cost, low thermal expansion, and other good properties.^3,13,19–21 In particular, the morphotropic phase boundary (MPB) of xPT–(1 − x)BMT ceramics is in the range of 0.36 ≤ x ≤ 0.38, with a relatively high T_C of about 700 K and piezoelectric coefficient d₃₃ above 200 pC N⁻¹.³ In order to avoid the redundant phase transition and improve the stability in a wide temperature range, we have systematically investigated the piezoelectric properties of tetragonal phase 0.62PT–0.38BMT single crystals, which can be considered as novel piezoelectric materials for high-performance actuators and transducers.²¹ According to the lattice dynamical theory and experiments, the A₁(1TO) soft mode in PT-based solid solutions is considered to be proportional to the parameter spontaneous polarization P_S.¹³ Especially in a PT-based ferroelectric system, where polarization is determined by the degree of local distortions, it is crucial to understand the structural behavior at the atomic level.²² Therefore, further investigation is necessary in order to illustrate the physical mechanism between the lattice dynamics and negative thermal expansion (NTE) of a 0.62PT–0.38BMT crystal. Up to now, a small amount of information could be found on the vibration behavior of a PT–BMT system, which is attributed to the difficult growth technology of pure perovskite BMT. Fortunately, the 0.62PT–0.38BMT crystals were successfully grown using a high-temperature solution method.²¹

In this work, we present the results from temperature dependent polarized Raman scattering experiments complemented by X-ray diffraction data, which depict the features regarding the local structure of the 0.62PT–0.38BMT single crystal. The anomalies were discussed according to the results of the unit cell volume and A₁(1TO) soft mode as a function of temperature. The results provide evidence of a consistent correlation between thermal expansion and P_S displacement.

2 Experimental details

The 0.62PT–0.38BMT powder and single crystals were grown using the flux-Bridgman method. Details about the crystal growth, microstructure and characterization can be found elsewhere.²¹ Structural analysis was undertaken using temperature-dependent X-ray diffraction (XRD), which was carried out using a Bruker D8 Discover High Resolution XRD in the temperature range from 300 to 873 K (TCU100 Temperature Control Unit, LNC Nitrogen Suction Equipment, Anton Paar). The temperature dependent Raman scattering was recorded on heating using a Jobin-Yvon LabRAM HR 800 micro-Raman spectrometer with the frequency range of 10–1000 cm⁻¹ and a THMSE 600 heating/cooling stage (Linkam Scientific Instruments) in the temperature range from 80 to 850 K. The crystals were excited using a 632.8 nm He–Ne laser and recorded in back-scattering geometry in parallel 〈x|zx|y〉 (VH) and perpendicular 〈x|zz|y〉 (VV) polarization configurations. The laser beam was focused through a 50× microscope with a working distance of 18 mm. An air-cooled charge coupled device (CCD) (−70 °C) with a 1024 × 256 pixels front illuminated chip was used to collect the scattered signal dispersed on 1800 grooves per mm grating with a resolution better than 1 cm⁻¹. The measured spectra have been treated with the Bose–Einstein phonon occupation factor and fitted with Lorentzian functions to determine the scattering information.^23–25

3 Results and discussion

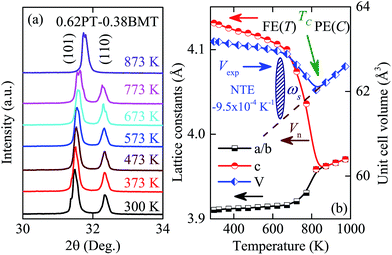
Room temperature (RT) XRD patterns of the 0.62PT–0.38BMT powder ground from the single crystals are shown in Fig. 1a and b. The single perovskite phase can be obtained according to the diffraction peaks, which is in good agreement with PDF #06-0452 and other literature.^6,13,16 The typical tetragonal symmetry can be characterized by the splitting of the (001) and (002) peaks at 22° and 44°, respectively. No impurity phases, such as Bi₁₂TiO₂₀ and Bi₄Ti₃O₁₂ phases, are observed in the composition presented here. The slight splitting of the (001) and (100) peaks from the 0.62PT–0.38BMT crystal can be found in Fig. 1b, indicating that the habitual faces of the grown crystals are {001}. The c/a ratio of the 0.62PT–0.38BMT single crystal is 1.061, which is much larger than that of PT–BMT in the MPB regions because the composition largely deviates from its MPB.²¹ Note that the c/a ratio of a single crystal is much larger than that of ceramics, suggesting a higher ferroelectricity and P_S.⁶

Fig. 1 The XRD patterns of the 0.62PT–0.38BMT powder, compared with the PDF card # 06-0452. The insert shows the XRD pattern of the 0.62PT–0.38BMT single crystal along the habitual face at room temperature.

High temperature XRD measurements were performed to identify the phase transition and the change of lattice parameters. Fig. 2(a) shows a typical transition of the tetragonal phase 0.62PT–0.38BMT crystal. The large splitting of the two diffraction peaks (101) and (110), representing the tetragonal phase, reduces with increasing temperature. When the temperature approaches above T_C (about 800 K), the two peaks merge into one, signifying that the cubic phase is dominant. Fig. 2(b) shows the lattice parameters [a(b) axis and c axis] and unit cell volume (abc) of the 0.62PT–0.38BMT system as a function of temperature. In the temperature range of 300–800 K, the c axis continually decreases while the a(b) axes slightly increase with increasing temperature. The unit cell volume, which is highly correlated with the change in ferroelectricity, contracts and reaches a minimum at T_C. Therefore, the temperature dependence of the XRD results demonstrates that the ferroelectric to paraelectric phase transition (FE–PE) of the 0.62PT–0.38BMT crystal is located at ∼800 K. Furthermore, it is interesting to find that temperature strongly affects the c axis of the 0.62PT–0.38BMT crystal when compared with the a(b) lattice parameters. Therefore, the unit cell volume is dominated by the c axis, which is also a common character for PT-based compounds.⁶

Fig. 2 (a) The transition of the (101) and (110) diffraction peaks of the 0.62PT–0.38BMT crystal with temperature. (b) Temperature dependence of the lattice parameters and unit cell volume of the 0.62PT–0.38BMT crystal. FE(T) and PE(C) mean ferroelectric tetragonal phase and paraelectric cubic phase, respectively. Note that the error bars are smaller than the symbol size.

According to the first-principle calculations and experimental results,⁴ the relatively small temperature dependence of the a(b) lattice parameters is related to the fact that the B-site Ti/Mg cation is more strongly covalent with four neighboring O2 oxygens in the ab plane than the two O1 oxygens (O1–Ti–O1) along the c axis. The stiff Ti–O2 bonds make compression and elongation in the ab plane energetically unfavorable, while the bonds of the O1–Ti–O1 unit along the c axis (the polar direction) are soft.^4,8 As shown in Fig. 2(b), 0.62PT–0.38BMT exhibits a very weakened NTE in the tetragonal phase. The volume coefficient of thermal expansion (CTE) α_V can be defined by the equation: . Where V_TC and V_RT are the unit cell volume at T_C and RT, respectively. In a lower temperature range (RT to 673 K), the unit cell volume shows little dependence on temperature with an average CTE of α_V = −7.3 × 10⁻⁴ K⁻¹. However, it contracts dramatically at elevated temperature with α_V = −3.5 × 10⁻³ K⁻¹ (673 to 800 K). The results demonstrate that the unit cell volume shrinks in the tetragonal phase but with a different slope as a function of temperature, which is similar to the results of the polar c axis length. The NTE in PT can be attributed to the thermal fluctuation of the cubic configurations in the tetragonal matrix.²⁶ The average CTE in the temperature range from RT to 800 K is α_V = −9.5 × 10⁻⁴ K⁻¹. Moreover, a high positive thermal expansion (PTE, α_V = −3.7 × 10⁻³ K⁻¹) could be found beyond the temperature of 800 K, indicating a structural phase transition.

It is known that two factors contribute to the unit cell volume of the ferroelectric phase: anharmonic lattice phonon vibration and ferroelectric order.⁶ With decreasing temperature, the contribution from the factor of anharmonic lattice phonon vibration decreases. Thus the nominal unit cell volume (V_n) should normally contract, which can be described using the Debye–Grüneisen model.^6,27 As shown in Fig. 2(b), V_n below T_C, which is only determined by anharmonic lattice phonon vibrations, should be the extrapolation from the high-temperature paraelectric phase to the low-temperature ferroelectric one. However, the experimental unit cell volume (V_exp) of PT–BMT actually shows an abnormal increase with decreasing temperature below T_C, signifying that the contribution from the ferroelectric order is simultaneously enhanced. The deviation of the unit cell volume from V_n to V_exp may be ascribed to the ferroelectric volume effect, which can be quantitatively described by spontaneous volume ferroelectrostriction (SVFS) using the equation: ω_s = (V_exp − V_n)/V_n × 100%.²⁸ As shown in Fig. 2(b), the value of SVFS for 0.62PT–0.38BMT is ω_s = 8.0% at RT, which gradually decreases with increasing temperature, and reaches zero at T_C (800 K). The mechanism of SVFS can be used to explain the phenomenon of NTE in the 0.62PT–0.38BMT crystals. It is known that the large ferroelectric polarization of PT-based compounds originates from the unique strong hybridization of the Pb 6s and O 2p orbitals, which stabilizes the large tetragonal distortion. This can be attributed to a stronger ferroelectric activity of A-site ions of Pb and Bi with a higher P_S displacement value of 0.45 Å and 0.80 Å, respectively. Therefore, there is strong coupling between P_S and NTE, which can be preliminarily characterized by the lattice dynamics results as follows.

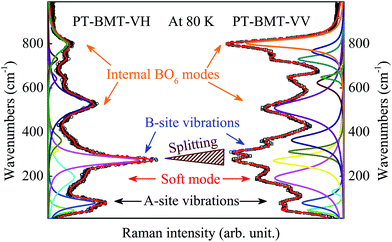
Raman spectroscopy is a sensitive technique for investigating structure modifications and phonon modes, which can give information on the changes of lattice vibrations and ferroelectricity.^25,29 For the tetragonal P4mm structure of 0.62PT–0.38BMT,¹⁶ a total of 8 optical lattice modes are predicted: Γ_P4mm = 3A₁ + 4E + B₁.^30,31 The simultaneous infrared and Raman activity produces additional splitting of each A₁ and E mode into longitudinal-optical and transverse-optical components, so that, up to 15 modes should be visible for the P4mm unit cells. However, the scattering efficiency from some of these modes may be weak, and, generally in PT-based materials, scattering contributes only by increasing the width of neighboring modes with a higher intensity. For the above reasons, all the Raman modes in PT-based materials are convoluted into three main observable peaks, and a complete assignment of the underlying phonon modes has never been reported.

Fig. 3 shows the polarized Raman spectra of the 0.62PT–0.38BMT single crystal at a representative temperature of 80 K. Spectral deconvolution was performed according to 13 Lorentzian peak functions by means of a best-fitting algorithm. The spectrum is consistent with previous reports of ABO₃-type ferroelectric materials, and can be linked to a tetragonal crystal structure. The three main regions can be distinguished in the spectrum; each of them has a relationship with different kinds of vibration in the lattice: (i) low frequency below 150 cm⁻¹, which can be associated with the vibrations of the perovskite A-site, involving Pb and Bi ions. According to the assignment of a PT single crystal,³¹ the Raman phonon modes at about 80 and 131 cm⁻¹ can be assigned to the E(1TO) and E(1LO) phonon modes, respectively. The presence of such distinct modes in the frequency range suggests possible cation ordering at the A-site. (ii) The frequency range of 150–450 cm⁻¹, which is related to the Ti–O/Mg–O stretching vibrations. In particular, the mode with the highest intensity in the VH geometry, at about 276 cm⁻¹, has been assigned as the B₁ + E mode, closely related to the strength of the Ti/Mg–O bond. The splitting of the Ti/Mg–O modes is found in the VV geometry, which is believed to correspond to a typical ferroelectric material.³² The A₁(1TO) soft mode at about 190 cm⁻¹ consists of displacements of the BO₆ octahedron relative to the Pb/Bi ions parallel to the P_S direction (c-axis). The ferroelectric soft mode is highly associated with the behavior dependence on temperature and will be discussed later in the present work. (iii) High frequency bands above 450 cm⁻¹ have all been associated with BO₆ vibrations, namely the breathing and stretching modes of the oxygen octahedra. It should be emphasized that the Pb-based ferroelectrics with aliovalent chemistry on the B site such as 0.62PT–0.38BMT exhibit relatively strong Raman scattering near 680–850 cm⁻¹, in contrast to the A-site complex with homovalent chemistry on the B site, such as (Na_0.5Bi_0.5)TiO₃–7%BaTiO₃ and (K_0.5Na_0.5)NbO₃–5%LiNbO₃.^33,34 The Raman scattering near 680–850 cm⁻¹ has been proven to arise from the symmetrical BO₆ stretching in a double-perovskite structure, which generates the A₁ mode in the cubic Fm3̄m structure. The local-scale doubling of the perovskite unit cell is attributed to the existence of a local-scale NaCl-type chemical B-site order even in compounds with no long-range B-site chemical order. The Raman spectra suggest a certain degree of local B-site chemical order for the 0.62PT–0.38BMT single crystal with simultaneous A-site and B-site doping.

Fig. 3 The polarized VH and VV Raman spectra of the 0.62PT–0.38BMT single crystal at a low temperature of 80 K. The peak assignment is based on the comparison with other perovskite-type ferroelectric oxides. The individual vibrational mode is fitted by using a Lorentz profile.

To further understand the relationship between lattice dynamics and NTE behavior for the 0.62PT–0.38BMT crystal, Fig. 4 presents the temperature dependence of the polarized Raman spectra in the temperature range from 80 to 850 K. With increasing temperature, the peak position and intensity of the polarized Raman phonon modes present a decreasing trend, while the broadening of the phonon modes is observed in the whole temperature range, which is similar to other ferroelectric materials.²⁹ It should be pointed out that the lowest intensity for all the phonon modes occurs at the temperature range of 600–700 K (marked by the dashed rectangles). A similar anomaly range can be found from the XRD results (different CTE values). Note that the change of the polarized Raman spectra above 700 K demonstrates that there are some minor structural changes in the tetragonal phase structure of the PT–BMT crystal. This phenomenon can be ascribed to the influence of the dynamics of the polar nanoregions (PNRs) and SVFS mechanism.

Fig. 4 Temperature evolution of Raman intensities for the 0.62PT–0.38BMT single crystal. The dashed rectangles mark the temperature ranges of the most pronounced changes.

The temperature dependence of the Raman phonon modes from the VV geometry is shown in Fig. 5. In the absence of any phase transition, one would expect steady phonon softening upon heating. However, in the case of the 0.62PT–0.38BMT crystal, one clear anomaly is visible at about 670 K. It should be emphasized that the reason for the anomaly is quite different from the phase transition temperature at about 800 K as determined using the XRD pattern and dielectric permittivity.²¹ The anomaly is an abrupt change in the wavenumber (softening of the phonon modes) that takes place in the A-site-related modes at about 670 K. The A₁(1TO) soft mode varies linearly as a function of temperature, which can be described using a harmonic model: . Where ω is the vibration frequency, k is the force constant related to the Pb/Bi–BO₆ bond strengths, and m* is the reduced mass of the soft mode. Furthermore, temperature dependent polarization can also be indicated by the variation of four short Pb/Bi–O2 bonds, since the Pb atom forms covalent bonds only with the four nearest-neighbor oxygens.^8,13 The Pb/Bi–O2 bonds elongate as a function of temperature for PT-based ferroelectric materials, suggesting a weakened Pb/Bi–O2 interaction followed by decreasing P_S displacement. The decreased P_S displacement of Pb/Bi introduces the centroids of Pb/Bi and BO₆ further, resulting in the decreased force constant k. On the other hand, with increasing temperature, the reduced P_S displacement makes the anharmonic potential energy shallow. As a result, the transition energy between excited states is reduced, and accordingly the vibration frequency ω of the soft mode is weakened. The tetragonality (c/a) in the PT–BMT single crystal could indicate NTE, since c/a is correlated with the lattice distortion. With increasing temperature up to T_C, the larger decrease of c/a for PT–BMT results in strong NTE, which is demonstrated in Fig. 2(b). The temperature dependence of c/a is strongly coupled with the Raman-active soft mode (i.e. NTE and P_S displacement) as shown by comparison of Fig. 2(b) and 5(b). Thus, it is apparent that there is a strong coupling interaction between P_S and NTE as determined using the soft mode and XRD patterns.

Fig. 5 (a) Temperature dependence of optical phonon frequencies for the ferroelectric tetragonal phase 0.62PT–0.38BMT single crystal. Note that the shaded parts approximately correspond to the temperature range of the changes in the phonon frequencies. (b) The phonon frequency of the A₁(1TO) soft mode as a function of temperature for the 0.62PT–0.38BMT crystal. The solid lines indicate the different decrements of the soft mode with temperature. The insert shows the vibration for the soft mode, which is associated with spontaneous polarization along the c-axis.

It is well-known that the PNRs are believed to play an important role in lead-based ferroelectric materials. Note that below the so-called Burns temperature (T_B), the temperature at which PNRs appear, the refractive index n, lattice parameters, unit cell volume V, or reciprocal dielectric permittivity 1/ε, begin to deviate from the linear changes of high temperatures.³⁵ The frequency of the soft mode actually shows an abnormal increase with decreasing temperature (at about 670 K), as shown in Fig. 5(b), indicating some structural changes. In the whole temperature range, two different slopes of lines are observed, which can be attributed to the variation of the soft mode frequency induced by the local P_S inside the PNRs. The d_A1(1TO)/d_T above and below T_B is about −0.011 and −0.030 cm⁻¹ K⁻¹, respectively. Similar abnormal results were found by Zhang et al.¹⁷ and Bokov et al.³⁵ using thermal expansion and dielectric measurements. The varying tendency of the A₁(1TO) soft mode frequency with temperature agrees well with the PNRs in Pb-based ferroelectrics, in which the unit cell volume deviates from the linear thermal expansion at T_B according to the XRD results in Fig. 2(b). Furthermore, as the temperature cools down from T_B, the effect of SVFS is evident due to the frozen PNRs.²⁸ Therefore, the NTE behavior of ferroelectrics is sensitive to spontaneous polarization displacement, which could be reflected by the A₁(1TO) soft mode. The present lattice dynamics observations further support the results demonstrated by the temperature dependent XRD measurements.

4 Conclusions

To summarize, with the detailed analysis of temperature dependent XRD and polarized Raman scattering results for the tetragonal 0.62PT–0.38BMT single crystal, we present clear experimental evidence for the mechanisms of NTE and P_S in structural phase transition driven by temperature. The T_C is found to be at about 800 K, which is suitable for high temperature piezoelectric devices. Furthermore, the major finding is that the lattice parameter, unit cell volume and frequency of the soft mode behavior in the tetragonal phase have abnormal shifts at about 670 K, which can be linked to the appearance of polar nanoregions and T_B. The present results show that the negative thermal expansion of the PT–BMT single crystal is correlated to its ferroelectricity and spontaneous polarization. The current study presents a novel method to characterize the relationship between the NTE and P_S of perovskite ferroelectric materials.

Acknowledgements

This work was financially supported by the Major State Basic Research Development Program of China (Grant No. 2013CB922300 and 2011CB922200), Natural Science Foundation of China (Grant No. 11374097 and 61376129), Projects of Science and Technology Commission of Shanghai Municipality (Grant No. 15JC1401600, 14XD1401500, 13JC1402100, and 13JC1404200), and the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning.

References

1. I. Grinberg, V. R. Cooper and A. M. Rappe, Nature, 2002, 419, 909.
2. D. D. Khalyavin, A. N. Salak, N. P. Vyshatko, A. B. Lopes, N. M. Olekhnovich, A. V. Pushkarev, I. I. Maroz and Y. V. Radyush, Chem. Mater., 2006, 18, 5104.
3. C. A. Randall, R. Eitel, B. Jones, T. R. Shrout, D. I. Woodward and I. M. Reaney, J. Appl. Phys., 2004, 95, 3633.
4. R. E. Cohen, Nature, 1992, 358, 136.
5. D. W. Wang, M. S. Cao and S. J. Zhang, J. Am. Ceram. Soc., 2012, 95, 3220.
6. J. Chen, L. Hu, J. X. Deng and X. R. Xing, Chem. Soc. Rev., 2015, 44, 3522.
7. X. B. Li, X. Y. Zhao, B. Ren, H. S. Luo, W. W. Ge, Z. Jiang and S. Zhang, Scr. Mater., 2013, 69, 377.
8. Y. Kuroiwa, S. Aoyagi, A. Sawada, J. Harada, E. Nishibori, M. Takata and M. Sakata, Phys. Rev. Lett., 2001, 87, 217601.
9. L. Zhang, Z. Xu, L. H. Cao and X. Yao, Mater. Lett., 2007, 61, 1130.
10. S. P. Zhang, X. H. Wang, J. L. Zhu, C. Q. Jin, H. L. Gong and L. T. Li, Scr. Mater., 2014, 82, 45.
11. F. F. Wang, L. L. Fan, Y. Ren, J. Chen and X. R. Xing, Appl. Phys. Lett., 2014, 104, 252901.
12. L. Zhang, Z. Xu, Z. R. Li, S. Xia and X. Yao, J. Electroceram., 2008, 21, 605.
13. J. Chen, K. Nittala, J. S. Forrester, J. L. Jones, J. Deng, R. B. Yu and X. R. Xing, J. Am. Chem. Soc., 2011, 133, 11114.
14. V. F. Freitas, O. A. Protzek, L. A. Montoro, A. M. Goncalves, D. Garcia, J. A. Eiras, R. Guo, A. S. Bhalla, L. F. Cótica and I. A. Santos, J. Mater. Chem. C, 2014, 2, 364.
15. T. Sebastian, I. Sterianou, D. Sinclair, A. Bell, D. Hall and I. Reaney, J. Electroceram., 2010, 25, 130.
16. A. Upadhyay and A. K. Singh, J. Appl. Phys., 2015, 117, 144102.
17. Q. Zhang, Z. R. Li and Z. Xu, Mater. Lett., 2011, 65, 3143.
18. L. B. Kong, T. S. Zhang, J. Ma and F. Boey, Prog. Mater. Sci., 2008, 53, 207.
19. P. H. Hu, J. Chen, X. Y. Sun, J. X. Deng, X. Chen, R. B. Yu, L. J. Qiao and X. R. Xing, J. Mater. Chem., 2009, 19, 1648.
20. T. Leist, J. Chen, W. Jo, E. Aulbach, J. Suffner and J. Rödel, J. Am. Ceram. Soc., 2012, 95, 711.
21. J. F. Liu, X. X. Chen, G. S. Xu, D. F. Yang, Y. F. Tian and X. Zhu, CrystEngComm, 2015, 17, 5605.
22. C. M. Foster, M. Grimsditch, Z. Li and V. G. Karpov, Phys. Rev. Lett., 1993, 71, 1258.
23. A. Dubroka, J. Humlíček, M. V. Abrashev, Z. V. Popović, F. Sapiña and A. Cantarero, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224401.
24. K. Datta, A. Richter, M. Göbbels, R. B. Neder and B. Mihailova, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 024107.
25. K. Jiang, W. W. Li, X. G. Chen, Z. N. Zhan, L. Sun, Z. G. Hu and J. H. Chu, J. Raman Spectrosc., 2012, 43, 583.
26. H. Z. Fang, Y. Wang, S. L. Shang and Z.-K. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024104.
27. F. Sayetat, P. Fertey and M. Kessler, J. Appl. Crystallogr., 1998, 31, 121.
28. J. Chen, F. F. Wang, Q. Z. Huang, L. Hu, X. P. Song, J. X. Deng, R. B. Yu and X. R. Xing, Sci. Rep., 2013, 3, 02458.
29. J. Z. Zhang, W. Y. Tong, J. J. Zhu, J. Y. Xu, Z. H. Duan, L. P. Xu, Z. G. Hu, C. G. Duan, X. J. Meng, Z. Q. Zhu and J. H. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085201.
30. M. D. Fontana, H. Idrissi, G. E. Kugel and K. Wojcik, J. Phys.: Condens. Matter, 1991, 3, 8695.
31. G. Burns and B. A. Scott, Phys. Rev. B: Solid State, 1973, 7, 3088.
32. J. Fu and R. Zuo, Acta Mater., 2013, 61, 3687.
33. T. Huang, S. Guo, L. P. Xu, C. Chen, Z. G. Hu, H. S. Luo and J. H. Chu, J. Appl. Phys., 2015, 117, 224103.
34. L. P. Xu, K. Jiang, J. Z. Zhang, G. S. Xu, Z. G. Hu and J. H. Chu, Appl. Phys. Lett., 2015, 106, 122901.
35. A. A. Bokov and Z. G. Ye, J. Mater. Sci., 2006, 41, 31.

---