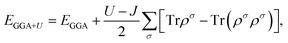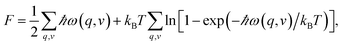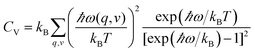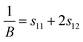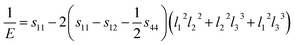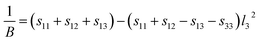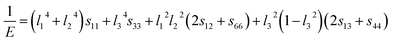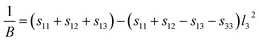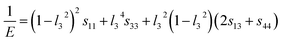Effect of carbon content and electronic strong correlation on the mechanical and thermodynamic properties of ytterbium carbides

Abstract

The mechanical and thermodynamic properties of four ytterbium carbides with increasing carbon content have been examined using ab initio calculations based on density functional theory. In order to describe the strong on-site Coulomb repulsion among localized 4f electrons, generalized gradient approximation plus a Hubbard parameter (GGA + U) formalisms have been adopted for the exchange correlation term. The elastic constants of YbC, Yb₂C₃, YbC₂, and YbC₆ are related to Hubbard U. The bulk modulus B, shear modulus G, and Young's modulus E are evaluated through Voigt–Reuss–Hill approximation. Among the four ytterbium carbides, YbC₆ yields the largest B, G, and E, and YbC₂ exhibits relatively soft and ductile characteristics. Mechanical anisotropy was estimated using several anisotropic indexes and factors. The anisotropic property of E of four ytterbium carbides is more evident than that of B. A phonon calculation reveals the thermodynamic stability of YbC₂ and YbC₆, which is consistent with experimental observations.

---

1. Introduction

Metal carbides have been extensively investigated from both experimental and theoretical points of view because of their unique magnetic and electrical properties for electronic applications.^1–4 Rare-earth carbides have been commonly used as model systems to probe structure–property relationships because of their structural diversity. C atoms play a principal role in the structural diversity of rare-earth carbides. The C-to-metal atomic ratio in rare-earth carbides exhibits a broad range, for instance, the C-to-metal atomic ratios of CeC and EuC₆ are 1 and 6, respectively.^5–7 The C atoms in rare-earth carbides also exist in various forms, such as three-dimensional networks, two-dimensional layered structures, and C–C dumbbell units. Two-dimensional C layers are implicated in superconducting graphite intercalation compounds (GICs). The combination of the graphene and intercalated sheets is accounted for superconductivity because neither graphite nor pure metal exhibits a high T_c.⁸ It is reported that the C–C dumbbell distance is correlated with T_c of rare-earth carbides superconductors.⁹ The C–C distance in the C₂ dumbbell at approximately 1.30 Å shows the highest T_c among rare-earth carbides. The C₂ dumbbell is also found in RE_xT_yC₂ carbides, where RE denotes a rare-earth metal and T denotes a transition metal. C₂ and T form a quasi-one-dimensional linear TC₄ unit embedded in matrix RE cations. It is found that the medium-frequency C₂ vibrations drive the high T_c in Sc₃CoC₄.¹⁰ Furthermore, C₂ dumbbell dimer unit could transfer to two-dimensional graphite sheets under pressure, such as in Ca–C systems.^11–13

The past decade has been seen intense efforts directed at studies of the structures and properties of ytterbium carbides. The ytterbium–carbon systems are significantly different from those of lightweight rare-earth carbide systems, which have well defined dicarbides, Pu₂C₃-type sequicarbides, and NaCl-type monocarbides.^14,15 However, NaCl-type monocarbides with a stoichiometric ratio of 1 : 1 has yet to be determined in Yb–C systems. Yb₃C is characterized by a C-deficient NaCl-type structure.¹⁴ Although Yb₂C₃ with a body-centered cubic Pu₂C₃-type structure can be prepared at high pressures, the thermodynamic stability of this compound under ambient conditions remains elusive.¹⁶ Similar to lightweight rare-earth carbides, YbC₂ assumes a tetragonal CaC₂-type structure.¹⁷ Surprisingly, the lattice parameters of YbC₂ are different from other rare-earth dicarbides. The lattice parameters of rare-earth carbides decrease regularly with increasing of atomic number of metal atoms, by contrast, the lattice parameters of YbC₂ lie between those of HoC₂ and ErC₂.¹⁴ The interest of ytterbium carbides is in part fueled by the discovery of superconductivity in YbC₆ with T_c of 6.5 K.¹⁸ Two mechanisms have been proposed to understand the superconductivity of GICs, including YbC₆. Csányi et al. proposed an unconventional exciton or plasmon-mediated pairing mechanism.¹⁹ Later, a conventional BCS phonon-mediated mechanism has also been suggested; in this mechanism, interlayer bands display a sufficiently strong coupling with both in-plane intercalant and out-of-plane graphite phonon modes to allow for a relatively high T_c.^20,21

4f electrons play a pivotal role in understanding the electronic and thermodynamic properties of rare-earth compounds; however, conventional density function theory (DFT), which uses conventional exchange-correlation potential, such as local density functional approximation (LDA) or generalized gradient approximation (GGA), has failed to describe the ground state properties of systems containing 4f electrons because of their strong on-site Coulomb repulsion. An effective modification of pure DFT which calls LDA/GGA + U (U is the Hubbard energy) scheme^22–24 can be used to obtain considerable improvement with respect to the LDA or GGA results. In fact, DFT + U calculations have been performed to explore the electronic properties of ytterbium compounds. Including localized 4f orbitals in the LDA + U method results in the downward rigid shift of the energy of the filled 4f bands in YbC₆.²⁵ The more recently studies of novel correlated topological insulator YbB₆ reveals that the 4f band moves to a higher energy and does not cross the 5d band when turning on the Hubbard parameter U; this findings is consistent with experimental data.²⁶

Although numerous studies on the structural and electronic properties of individual ytterbium carbide have been performed, theoretical studies on ytterbium carbides, especially mechanical and thermodynamic properties with respect to carbon contents have been rarely conducted. In addition, the effects of electronic strong correlation on ytterbium carbides have been sparsely visited. In this work, four representative ytterbium carbides with increasing carbon contents (YbC, Yb₂C₃, YbC₂, and YbC₆) were selected to systematically examine their mechanical and thermodynamic properties through ab initio GGA + U calculations.

2. Computational methods

The ab initio calculations were performed within the framework of DFT as implemented in the Vienna Ab-initio Simulation Package (VASP).²⁷ The all-electron projector augmented wave (PAW)²⁸ pseudopotential for Yb and C from the VASP pseudopotential library were used. The electron wave function was expanded in plane waves up to a cutoff energy of 550 eV. The k-point meshes²⁹ in the full edge of the Brillouin zone (BZ) are sampled of 2π × 0.02 Å⁻¹. Iteration relaxation of atomic positions and cell volume was stopped when the forces generally acting on the atoms were found to be smaller than 0.01 eV Å⁻¹. With this criterion, the change in total energy between successive steps was less than 0.01 meV per cell. The exchange and correlation energy was assessed by GGA in the scheme of Perdew–Burke–Ernzerhof (PBE).³⁰ The strong on-site Coulomb repulsion among the localized Yb 4f electrons was described by the DFT + U method^22,24 developed by Dudarev et al.²³ In this scheme, the total GGA energy functional is defined as:
where ρ^σ is the density matrix of f states with spin σ, U and J are the spherically averaged screened Coulomb energy and exchange energy, respectively. Since only the difference between U and J is significant, thus we will henceforth label them as one single parameter U for simplicity, In the subsequent calculations, the parameter U varies from 1 to 5, and U = 0 means turning off the Hubbard U term.

Phonon calculations were performed by supercell approach and finite displacement method.³¹ From finite displacements, the Hellmann–Feynman atomic forces computed at the optimized supercell by VASP code were transferred to the PHONOPY code^32,33 to construct the dynamical matrix. Diagonalization of the dynamical matrix gives phonon frequencies and their corresponding density of states. In the interpolation of the constants for calculating the phonon dispersion, 3 × 3 × 3, 2 × 2 × 2, 3 × 3 × 3, and 2 × 2 × 1 supercells with k-point mesh of 2π × 0.02 Å⁻¹ were used for YbC, Yb₂C₃, YbC₂ and YbC₆ respectively. Thermodynamic properties can be determined by phonon calculations using the quasiharmonic approximation (QHA).³³ The phonon contribution to the Helmholtz free energy F is given by:

where ω(q, v) is the phonon frequency at wave vector q and band v, and T is the temperature. k_B and ℏ are the Boltzmann constants and the reduced Planck constants, respectively. The heat C_V and S are given by
and
respectively.

3. Results and discussion

3.1 Equilibrium structural properties

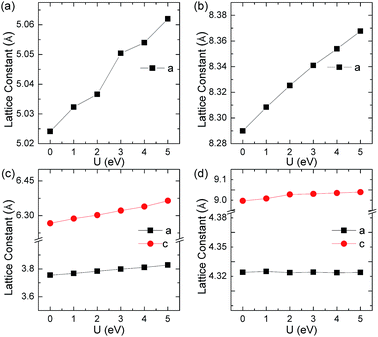
YbC with a stoichiometric ratio of 1 : 1 adopts an ordered cubic NaCl-type structure (space group Fm3̄m), in which Yb atoms assume Na positions and C atoms occupy Cl positions, as shown in Fig. 1(a). The Yb atoms form a close-packed structure, whereas the C atoms enter octahedral interstices. The lattice constant a of YbC with various Hubbard U values are presented in Fig. 2(a). The lattice constants display a ladder shape as Hubbard U values increase. When Hubbard U is turned off, the calculated lattice constant a reaches 5.024 Å, which is the smallest value. At Hubbard U = 5 eV, the lattice constant a is 5.062 Å. Ytterbium sequicarbides, Yb₂C₃, assumes a cubic Pu₂C₃-type crystal structure (space group I4̄3d) with eight formula units (fu) in a conventional cell. The Yb atoms are aligned along the [111] direction, and the C atoms form dumbbell-shaped dimers occupying the voids in the bisphenoids of the Yb substructure. The calculated lattice constant a as a relationship of Hubbard U is shown in Fig. 2(b). The calculated lattice constant a of 8.290 Å at Hubbard U = 0 eV is 2.7% larger than the experimental value of 8.073 Å.¹⁶ Furthermore, the calculated C–C distances slightly decrease as Hubbard U value increases, from 1.314 Å at Hubbard U = 0 eV to 1.303 Å at Hubbard U = 5 eV. However, the difference between the calculated C–C distances with various Hubbard U values within 0.2% and the C–C dimer distances of Yb₂C₃ are close to the experimental value of 1.313 Å.¹⁶

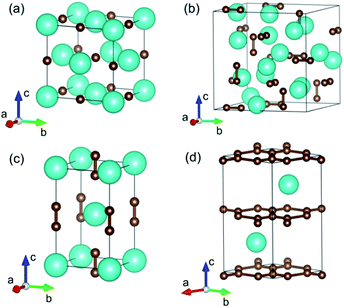Fig. 1 Crystal structures of (a) YbC, (b) Yb₂C₃, (c) YbC₂, and (d) YbC₆. The large and small spheres represent Yb and C atoms, respectively.

Fig. 2 Lattice constants as a function of Hubbard U for (a) YbC, (b) Yb₂C₃, (c)YbC₂, and (d) YbC₆.

YbC₂ crystallizes in a body-centered tetragonal CaC₂-type structure (space group I4/mmm), in which the C atoms exist in the form of a C–C dimer similar to that in Yb₂C₃. The C–C dimers oriented parallel to the c axis are six-fold coordinated by Yb atoms forming an elongated octahedron. As the Hubbard U increases from 0 eV to 5 eV, the lattice constants a and c increase by 1.9% and 1.6%, respectively. The calculated C–C dimer distances in YbC₂ with various Hubbard U remain almost unchanged and reach the experimental value of 1.293 Å.¹⁷ Moreover, it is noteworthy that the C–C dimer distance in other Pu₂C₃- and CaC₂-type rare-earth carbides is approximately 1.3 Å, such as 1.298 Å in Y₂C₃,³⁴ 1.2942 Å in La₂C₃,³⁵ 1.2888 Å in YC₂,³⁶ and 1.303 Å in LaC₂.³⁷ This result indicates that the C–C dimer distance shows a weak dependence on the choice of metal atoms in these crystals.

Thus, it is not unexpected that the C–C dimer distances in Yb₂C₃ and YbC₂ change slightly with various Hubbard U because the Hubbard U correction is added on the 4f electrons of the Yb atoms. YbC₆, a famous kind of GICs, presents an AαAβ stacking where A corresponds to C layers and α and β represent the Yb intercalant layers. Interestingly, the lattice constant c significantly increases when Hubbard U increases; by contrast, the lattice constant a seems unaffected to Hubbard U and is approximately equals to 4.340 Å, which is close to the experimental value of 4.320 Å^6,7 and the theoretical value of 4.340 Å.³⁸ In fact, the lattice parameters a slightly differs in other GICs, such as 4.29 Å of NdC₆, and 4.314 Å of EuC₆.^6,7

3.2 Elastic constants and polycrystalline moduli

The elastic constants of a solid link the mechanical and dynamical behaviors and provide important information regarding the nature of the forces operating in the solids, such as stability and stiffness. The independent elastic constants of YbC, Yb₂C₃, YbC₂ and YbC₆ with various Hubbard U values are calculated from the strained structures, and the relationship between independent elastic constants and Hubbard U values is plotted in Fig. 3. There are three independent elastic constants for cubic YbC and Yb₂C₃, i.e., C₁₁, C₁₂, and C₄₄. The elastic constants of YbC and Yb₂C₃ decrease as Hubbard U increases except C₁₂ of YbC. The elastic constant C₁₂ of YbC first falls to 40.1 GPa at Hubbard U = 3 eV and then rises to 50 GPa at Hubbard U = 5 eV, forming a valley at Hubbard U = 3 eV, as shown in Fig. 3(a). For the relatively low-symmetry tetragonal YbC₂ and hexagonal YbC₆, there are six independent elastic constants. Similar to the elastic constants of YbC and Yb₂C₃ systems, most of the elastic constants of YbC₂ and YbC₆ decrease when Hubbard U increases. The elastic constant C₃₃ of YbC₂ and YbC₆ decreases by approximately 23% and 14% from Hubbard U = 0 eV to 5 eV, respectively. Interestingly, the elastic constant C₁₃ of YbC₂ and YbC₆ initially decreases and then increases as Hubbard U increases. The elastic constant C₁₁ of YbC₆ is the largest among the elastic constants of the four ytterbium carbides; in particular, C₁₁ of YbC₆ is 719 GPa and 713 GPa at Hubbard U = 0 and 5 eV, respectively. Moreover, the elastic constant C₆₆ of YbC₆ remains unchanged at 314 GPa with Hubbard U, as shown in Fig. 3(d). When the independent elastic constants are obtained, the intrinsic mechanical stability of the structure at various Hubbard U = 0, 1, 3 and 5 eV can be verified by the Born–Huang lattice dynamical theory. The criteria to determine the mechanical stability of cubic, tetragonal and hexagonal crystals are depicted as follows:³⁹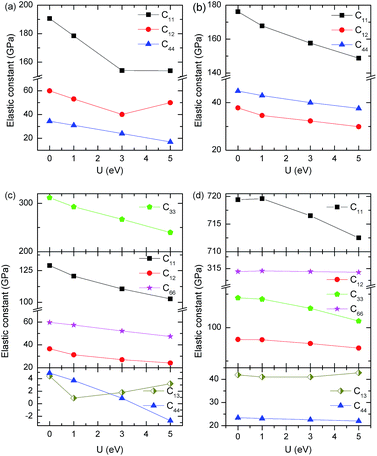

Fig. 3 Dependence of the elastic constants on Hubbard U for (a) YbC, (b) Yb₂C₃, (c) YbC₂, and (d) YbC₆.

Cubic phase (for YbC and Yb₂C₃):

C₁₁ − C₁₂ > 0, C₁₁ + 2C₁₂ > 0, C₄₄ > 0.

Tetragonal phase (for YbC₂):

C₁₁ > |C₁₂|, (C₁₁ + 2C₁₂)C₃₃ > 2C₁₃², C₄₄ > 0, C₆₆ > 0.

Hexagonal phase (for YbC₆):

C₁₁ > |C₁₂|, (C₁₁ + 2C₁₂)C₃₃ > 2C₁₃², C₄₄ > 0.

After these criteria are verified, the four ytterbium carbides with various Hubbard U values satisfy the criteria of mechanical stability except tetragonal YbC₂ with Hubbard U = 5 eV where C₄₄ is negative. Specially, it is worth noticing that the NaCl-type YbC is mechanically stable, although this carbide has not been synthesized successfully.

Mechanical properties are mainly determined by the quantity including bulk modulus B, Young's modulus E, shear modulus G, Pugh's ratio B/G and Poisson's ratio ν. Among these mechanical quantities, B and G can be obtained by Voigt–Reuss–Hill (VRH) approximation.^40–42 Under the VRH B_V, B_R, G_V, and G_R, where the subscripts V and R represent Voigt and Reuss estimations of B and G, respectively, in different crystal systems can be expressed as follows:

Cubic phase (for YbC and Yb₂C₃):^43,44

B_V = B_R = (C₁₁ + 2C₁₂)/3,

G_V = (C₁₁ − C₁₂ + 3C₄₄)/5,

G_R = 5(C₁₁ − C₁₂)C₄₄/[4C₄₄ + 3(C₁₁ − C₁₂)].

Tetragonal phase (for YbC₂):⁴⁵

B_V = (1/9)[2(C₁₁ + C₁₂) + 4C₁₃ + C₃₃],

B_R = C²/M,

G_V = (1/30)(M + 3C₁₁ − 3C₁₂ + 12C₄₄ + 6C₆₆),

G_R = 15[18B_V/C² + 6/(C₁₁ − C₁₂) + 6/C₄₄ + 3/C₆₆]⁻¹,

M = C₁₁ + C₁₂ + 2C₃₃ − 4C₁₃,

C² = (C₁₁ + C₁₂)C₃₃ − 2C₁₃².

Hexagonal phase (for YbC₆):⁴⁶

B_V = (1/9)[2(C₁₁ + C₁₂) + 4C₁₃ + C₃₃],

B_R = C²/M,

G_V = (1/30)(M + 12C₄₄ + 12C₆₆),

G_R = (5/2)[C²C₄₄C₆₆]/[3B_VC₄₄C₆₆ + C²(C₄₄ + C₆₆)],

M = C₁₁ + C₁₂ + 2C₃₃ − 4C₁₃,

C² = (C₁₁ + C₁₂)C₃₃ − 2C₁₃².

Hence, B and G are given as follows:

B = 1/2(B_R + B_V) and G = 1/2(G_R + G_V).

Once B and G are obtained, E and υ can be defined as follows:

E = 9BG/(3B + G) and υ = (3B – 2G)/[2(3B + G)].

The dependence of B_V, B_R, G_V, and G_R on Hubbard U of YbC, Yb₂C₃, YbC₂, and YbC₆ is shown in Fig. 4. B_V, B_R, G_V, and G_R likely decrease as Hubbard U values increases except B_V and B_R of YbC. B_V and B_R of YbC first decreases from 103.5 GPa at U = 0 eV to 78.1 GPa at U = 3 eV and then increases to 84.7 GPa at U = 5 eV in accordance with the relationship of C₁₁ and C₁₂ as Hubbard U. By contrast, Hubbard U slightly affect B and G of YbC₂ and YbC₆, and this result is consistent with the variation in elastic constants.

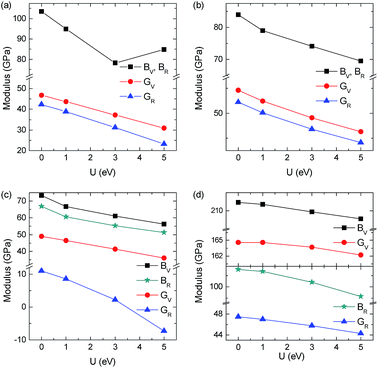Fig. 4 Calculated bulk modulus B and shear modulus G of YbC, Yb₂C₃, YbC₂ and YbC₆ under Voigt and Reuss approximations with various Hubbard U values.

Bulk modulus B is measure of the resistance of a solid to volume change; shear modulus G represents the resistance to plastic deformation; and Young's modulus E denotes the resistance to uniaxial deformation. The calculated B, G, and E of the four ytterbium carbides with Hubbard U = 3 eV are listed in Table 1. Among the four ytterbium carbides, YbC₆ yields the largest B of 155.9 GPa, G of 104.8 GPa, and E of 256.7 GPa. This result indicates that YbC₆ is stiffer than the three other ytterbium carbides. On the contrary, YbC₂ exhibits the smallest B of 58.2 GPa, G of 21.7 GPa, and E of 58.0 GPa. B of YbC₂ is only approximately one-third of that of YbC₆. Hardness and ductile will not coexist in a material. The ductile or brittle properties of materials can be related empirically to Pugh's ratio B/G. If B/G > 1.75, materials are ductile; otherwise, materials are brittle.⁴⁷ The smallest B/G of 1.49 observed in YbC₆ indicates brittleness. The largest B/G of 2.68 is detected in YbC₂; this finding shows that YbC₂ is relatively soft and ductile. Poisson's ratio ν generally quantifies the stability of a solid against shear deformation. For ductile materials, ν is approximately 0.33.⁴⁸ The ductility of YbC₂ is confirmed by the calculated ν of 0.33. Interestingly, B and G of YbC and Yb₂C₃ yield the same order of magnitude; however, B/G of YbC and Yb₂C₃ is more or less 1.75; thus, these carbides exhibit different degrees of brittleness.

Table 1 Bulk modulus B, shear modulus G, Young's modulus E, Pugh's ratio B/G, and Poisson ratio ν calculated with VRH approximations of YbC, Yb₂C₃, YbC₂ and YbC₆ at Hubbard U = 3 eV

	B (GPa)	G (GPa)	E (GPa)	B/G	ν
YbC	78.1	34.2	89.6	2.28	0.309
Yb2C3	74.1	47.9	118.2	1.55	0.240
YbC2	58.2	21.7	58.0	2.68	0.334
YbC6	155.9	104.8	256.7	1.49	0.226

---

3.3 Elastic anisotropy

Anisotropic behaviors should be estimated on the basis of fundamental and technological aspects because known crystals are elastically anisotropic. Several indexes, including the percent anisotropy (A_B and A_G) and shear anisotropic factors (A₁, A₂, and A₃) have been developed to evaluate elastic anisotropy.⁴⁹ The percent anisotropy in compressibility and shear are defined as follows:

A_B = (B_V − B_R)/(B_V + B_R)

and

A_G = (G_V − G_R)/(G_V + G_R),

respectively. For a completely isotropic system, A_B and A_G are 0, and the deviation from 0 measures the degree of elastic anisotropy. As shown in Table 2, the percent anisotropies in the shear A_G of high-symmetry cubic YbC and Yb₂C₃ systems are 0.0877 and 0.0240, respectively; whereas A_B equals 0 because of the same B_V and B_G. YbC₆ possesses the largest A_B of 0.3455 and a moderate A_G of 0.5268, whereas YbC₂ yields the largest A_G of 0.8989. This result indicates that YbC₂ displays a large anisotropy in shear. It is should be noted that A_G of the four ytterbium carbides is larger than A_B, suggesting that these carbides are slightly anisotropic in compressibility.

Table 2 Percent anisotropy (A_B and A_G) and shear anisotropic factors (A₁, A₂, and A₃) of YbC, Yb₂C₃, YbC₂, and YbC₆ at Hubbard U = 3 eV

	AB	AG	A1	A2	A3
YbC	0	0.0877	0.4211	0.4211	0.4211
Yb2C3	0	0.0240	0.6385	0.6385	0.6385
YbC2	0.0490	0.8989	0.0095	0.0095	1.2488
YbC6	0.3455	0.5628	0.1207	0.1207	0.9997

---

Shear anisotropic factors correspond to the degree of anisotropy in the bonding between atoms in different planes. A₁ of the (100) shear planes between [011] and [010] directions, A₂ of the (010) shear planes between [101] and [001] directions, and A₃ of the (001) shear planes between [110] and [010] directions are defined as follows:

A₁ = (4C₄₄)/(C₁₁ + C₃₃ − 2C₁₃),

A₂ = (4C₅₅)/(C₂₂ + C₃₃ − 2C₂₃),

and

A₃ = (4C₆₆)/(C₁₁ + C₂₂ − 2C₁₂).

The three indexes must be identical for a completely isotropic system, and any deviation from unity corresponds to the degree of shear anisotropy. A₁, A₂, and A₃ are identical in YbC and Yb₂C₃ because of the shear isotropy of cubic structure. A₁ of YbC₂ is smaller than that of YbC₆, indicating that YbC₂ behaves more (100) shear anisotropically than YbC₆. A₃ of 0.9997 of YbC₆ demonstrates the almost isotropic property of (001) shear planes between [110] and [100] directions.

A three-dimensional surface construction of B and E, along with their projections on specific planes, is plotted to describe the anisotropy of the mechanical moduli of the four ytterbium carbides. The reciprocal of B and E are defined as follows:⁵⁰

Cubic phase (for YbC and Yb₂C₃):

Tetragonal phase (for YbC₂):

Hexagonal phase (for YbC₆):

where l₁, l₂, and l₃ are the direction cosines in various systems, and s_ij is elastic compliance constant obtained using the GGA + U scheme with Hubbard U = 3 eV.

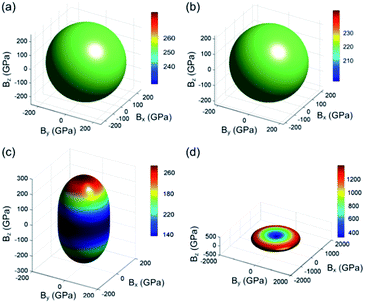
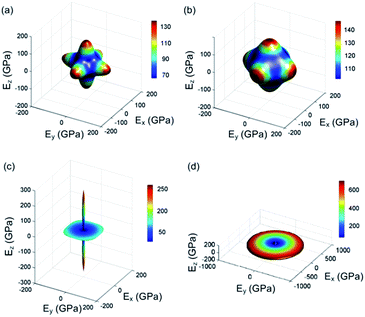
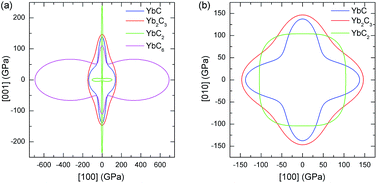
The surface constructions of B of YbC, Yb₂C₃, YbC₂, and YbC₆ are displayed in Fig. 5, and their B projections on the (010) and (001) planes are plotted in Fig. 6. The surface constructions of B of YbC and Yb₂C₃ exhibit a perfect sphere, indicating isotropic characteristics because of high-symmetry cubic lattice, see Fig. 5(a) and (b). B of tetragonal YbC₂ and hexagonal YbC₆ shows strong anisotropic features. The surface construction of B of YbC₂ is likely an ellipsoid, see Fig. 5(c), whereas the surface of B of YbC₆ is similar to a disc, see Fig. 5(d). It is worth noticing that these results are in good agreement with the calculated anisotropic factors and indexes listed in Table 2. B projections on the (010) and (001) planes provide further details regarding anisotropic properties. The x axis range is five times larger than the y axis range to display B projections of the four carbides. The B projection on the (010) plane of YbC and Yb₂C₃, resembling an ellipse in Fig. 6(a), should be a circle. The B projection on the (010) plane of YbC₆ exhibits a butterfly shape, showing a strong anisotropic property. B projected on the (001) plane of the four ytterbium carbides is circular, which indicates an isotropic property. Due to the large B of YbC₆, the circular B on the (001) plane is noticeably larger than the three other ytterbium carbides. Fig. 6(b) illustrates only B of YbC, Yb₂C₃, and YbC₂ but excludes B of YbC₆ to show the B projection. The circular area of YbC is slightly larger than that of Yb₂C₃, which is consistent with B listed in Table 1.

Fig. 5 Surface constructions of bulk modulus B of (a) YbC, (b) Yb₂C₃, (c) YbC₂, and (d) YbC₆.

Fig. 6 Bulk modulus B projections on (a) (010) and (b) (001) plane of YbC, Yb₂C₃, YbC₂, and YbC₆.

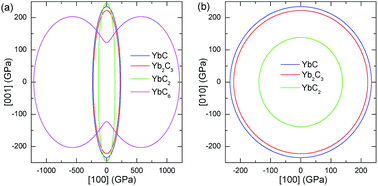
The surface constructions of E of YbC, Yb₂C₃, YbC₂, and YbC₆ are displayed in Fig. 7, and E projections on the (010) and (001) planes are plotted in Fig. 8. The anisotropic property of E of YbC, Yb₂C₃, YbC₂, and YbC₆ is more evident than that of B. The surface constructions of E of YbC and Yb₂C₃ resemble a similar shape, see Fig. 7(a) and (b). E along the [100], [010], and [001] directions are considerably larger than E along other directions, indicating anisotropic features. From Fig. 8(b), it can be seen that E of YbC projection on the (001) plane is smaller than that of Yb₂C₃, which is consistent with that of VRH approximations listed in Table 1. The surface construction of E of YbC₂ is similar to a fishing float with a large value along the [001] direction, showing a strong anisotropic property. The projection of E of YbC₂ exhibits a rounded square, as seen in Fig. 8(b). Similar to the surface construction of B, the surface construction of E of YbC₆ is similar to a disc perpendicular to the [001] direction. Interestingly, E of YbC₆ in the [100] direction is obviously larger than that in the [001] direction, as shown in Fig. 8(a). The projection E on the (001) plane of YbC₆ is a circle but is not shown in Fig. 8(b) because of its large area.

Fig. 7 Surface constructions of Young's modulus E of (a) YbC, (b) Yb₂C₃, (c) YbC₂, and (d) YbC₆.

Fig. 8 Young's modulus E projections on (a) (010) and (b) (001) plane of YbC, Yb₂C₃, YbC₂, and YbC₆.

3.4 Anisotropy in acoustic velocities

The phase velocities of pure transverse and longitudinal modes of YbC, Yb₂C₃, YbC₂, and YbC₆ are investigated from single crystal elastic constants in accordance with the procedure developed by Brugger.^51,52 The symmetry of crystal indicates that pure transverse and longitudinal modes can exist along specific directions: [001], [110], and [111] for a cubic crystal; [001], [110], and [100] for a tetragonal crystal; and [001] and [110] for a hexagonal crystal. In each direction, two transverse modes and one longitudinal mode are involved.⁵³ The calculated sound velocities of ytterbium carbides with Hubbard U = 3 eV are shown in Table 3.

Table 3 Sound velocities (km s⁻¹) along different directions for YbC, Yb₂C₃, YbC₂ and YbC₆ with Hubbard U = 3 eV

		YbC	Yb2C3	YbC2	YbC6
[001]	[001]vl	4.019	4.245	6.101	4.563
	[110]vt1	1.586	2.139	0.354	2.028
[110]	[110]vl	3.847	4.157	4.108	11.419
	[1̄10]vt1	2.445	2.677	2.414	7.562
	[001]vt2	1.586	2.139	0.354	2.028
[111]	[111]vl	3.397	3.817
	[112̄]vt1	2.196	2.510
[100]	[100]vl			3.927
	[010]vt1			2.698
	[001]vt2			0.354

---

In the two cubic phases, the sound velocities of Yb₂C₃ are larger than those of YbC in the [001], [110], and [111] directions. For example, the longitudinal and transverse mode velocities of Yb₂C₃ in the [001] direction are 5.6% and 34.8% larger than those of YbC. The longitudinal and transversemode velocities of the cubic system are proportional to C₁₁ and C₄₄, respectively, and are inversely proportional to the density ρ which is dominated by carbon contents. C₁₁ and C₄₄ of Yb₂C₃ are larger than those of YbC, and the density ρ of Yb₂C₃ is smaller than that of YbC due to the relatively higher carbon contents. This leads to that the average sound velocities of Yb₂C₃ are larger than that of YbC, as shown in Fig. 9. The longitudinal and transverse vibration modes in the [001] direction of YbC₂ are parallel and perpendicular to the C₂ dimer stretching mode. Thus, YbC₂ yields a relatively larger longitudinal mode velocity of 6.10 km s⁻¹ and an extremely low transverse mode velocity of 0.35 km s⁻¹. Moreover, the significant difference between the transverse and longitudinal velocities in the [001], [100], and [110] directions results in relatively low average velocities, as shown in Fig. 9.

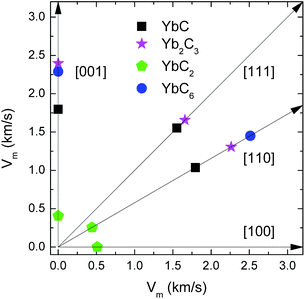Fig. 9 Averaged sound velocities (v_m) in the [100], [001], [110] and [111] directions of YbC, Yb₂C₃, YbC₂, and YbC₆.

The longitudinal mode velocity in the [110] direction of YbC₆ is as high as 11.42 km s⁻¹, whereas two transverse mode velocities along [1̄10] and [001] directions are 7.562 km s⁻¹ and 2.028 km s⁻¹, respectively. The sound velocity is well correlated with the structural characteristics. The longitudinal mode [110]v_l direction is the nearest C–C connecting direction in the six-membered C ring; conversely, the transverse mode [1̄10]v_t1 direction is the second-nearest C–C connecting direction in the six-membered C ring. Furthermore, the large longitudinal mode velocity in the [110] direction corresponds the highest average velocity along the [110] direction among the four ytterbium carbides.

3.5 Thermodynamic properties

The calculated phonon band structures along some high-symmetry directions in Brillouin zone and the phonon projected density of states (PDOS) of YbC₂ and YbC₆ at Hubbard U = 3 eV are displayed in Fig. 10. Phonon calculations established the dynamical stability of YbC₂ and YbC₆ in view of the absence of imaginary frequencies. Additional phonon calculations of YbC and Yb₂C₃ with various Hubbard U parameters and sizes of supercells are performed. The results show that imaginary frequencies exist in their phonon band structures (data not shown here). This finding reveals that YbC and Yb₂C₃ are not thermodynamically stable, which does not coincide with the mechanical stability. This phenomenon is also found in UO₂. The Pnma phase of UO₂ is predicted to be mechanically stable, but is found to be thermodynamically unstable from phonon calculations.⁵⁴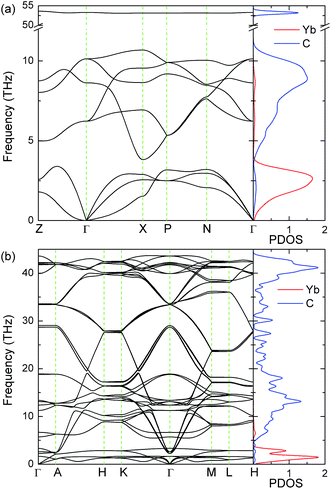

Fig. 10 Phonon band structures and PDOS of (a) YbC₂ and (b) YbC₆ with Hubbard U = 3 eV. The unit of PhDOS is states/THz/fu.

The vibration frequency of the Yb atom is apparently lower than that of the C atom because the Yb atom is considerably heavier than C atom. Thus, the phonon structures of both YbC₂ and YbC₆ can be divided into two major regions. The heavy Yb atoms dominate low-frequency modes below 4 THz, whereas the light C atoms contribute significantly to high-frequency vibrations. Compared with YbC₆, the high-frequency region of YbC₂ shifts upward and reaches approximately 53 THz. It is noteworthy that the flat regions of the phonon dispersion curves of YbC₂ as shown in Fig. 10(a), which correspond to the peaks in the phonon PDOS, indicate the localization of the states, i.e., the high-frequency stretching of C₂ units.

The temperature variations of Helmholtz free energy, entropy, and heat capacity at constant volume of YbC₂ and YbC₆ are shown in Fig. 11. It is noteworthy that the Helmholtz free energy at 0 K does not vanish because of zero-point motion. Helmholtz free energies per fu of YbC₂ and YbC₆ are 20.1 and 90.7 kJ mol⁻¹, respectively. As temperature increases, Helmholtz free energies of YbC₂ and YbC₆ decrease; however, Helmholtz free energy of YbC₆ rapidly decreases, leading to that it intersects with the Helmholtz free energy of YbC₂ at 1350 K. The entropy of YbC₆ is larger than that of YbC₂, and the difference between the entropies of these carbides increases as temperature increases. The heat capacity at constant volume of YbC₆ and YbC₂ is nearly the same below 200 K. At an intermediate temperature range, C_V is governed by atomic vibrations. Above 200 K, C_V of YbC₆ is larger than that of YbC₂. At high temperature, C_V of YbC₂ becomes constant at 75 J mol⁻¹ K, while C_V of YbC₆ reaches 170 J mol⁻¹ K⁻¹.

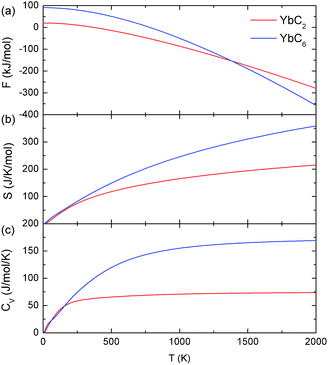Fig. 11 Temperature dependence of (a) Helmholtz free energy (F), (b) entropy (S), and (c) heat capacity at constant volume (C_V) of YbC₂ and YbC₆ with Hubbard U = 3 eV.

4. Conclusions

The mechanical and thermodynamic properties of YbC, Yb₂C₃, YbC₂, and YbC₆ have been investigated with the GGA + U frameworks. The calculated lattice constants of YbC, Yb₂C₃, YbC₂, and YbC₆ are found to increase as Hubbard U values increase. The four ytterbium carbides with various Hubbard U values satisfy the Born–Huang lattice dynamical criteria of mechanical stability except tetragonal YbC₂ with Hubbard U = 5 eV. YbC₆ is stiffer than the three other ytterbium carbides, whereas YbC₂ is softest and most ductile among the four ytterbium carbides. The directional E and B, and shear anisotropic factors indicate the mechanical anisotropic properties of YbC, Yb₂C₃, YbC₂ and YbC₆. The phonon calculation reveals that YbC₂ and YbC₆ are thermodynamically stable, but NaCl-type YbC and Pu₂C₃-type Yb₂C₃ are thermodynamically unstable. These theoretical results are consistent with experimental findings.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants No. 11304269 and 11304268).

References

1. K. A. Gschneider, Rare earth carbides, 1991.
2. M. S. Sselhaus and G. Sselhaus, Adv. Phys., 2002, 51, 1–186.
3. S. Ma, K. Bao, Q. Tao, X. Huang, P. Zhu and T. Cui, RSC Adv., 2014, 4, 63544–63548.
4. D. D. Kumar, N. Kumar, S. Kalaiselvam, R. Radhika, S. Dash, A. K. Tyagi and R. Jayavel, RSC Adv., 2015, 5, 81790–81801.
5. L. Brewer and O. Krikorian, J. Electrochem. Soc., 1955, 103, 701–703.
6. M. E. Makrini, D. Guérard, P. Lagrange and A. Hérold, Physica B+C, 1980, 99, 481–485.
7. M. E. Makrini, D. Guérard, P. Lagrange and A. Hérold, Carbon, 1980, 18, 203–209.
8. M. H. Upton, T. R. Forrest, A. C. Walters, C. A. Howard, M. Ellerby, A. H. Said and D. F. McMorrow, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134515.
9. V. Babizhetskyy, O. Jepsen, R. K. Kremer, A. Simon, B. Ouladdiaf and A. Stolovits, J. Phys.: Condens. Matter, 2014, 26, 025701.
10. C. Zhang, S. T. John, T. Kaori and H. Q. Lin, EPL, 2012, 100, 67003.
11. Y. L. Li, W. Luo, Z. Zeng, H. Q. Lin, H. K. Mao and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9289–9294.
12. Y. L. Li, S. N. Wang, A. R. Oganov, H. Gou, J. S. Smith and T. A. Strobel, Proc. Natl. Acad. Sci. U. S. A., 2015, 6, 6974.
13. Y. L. Li, W. Luo, X. J. Chen, Z. Zeng, H. Q. Lin and R. Ahuja, Sci. Rep., 2013, 3, 3331.
14. F. H. Spedding, K. Gschneidner and A. H. Daane, J. Am. Chem. Soc., 1958, 80, 4499–4503.
15. J. M. Haschke and H. A. Eick, J. Am. Chem. Soc., 1970, 92, 1526–1530.
16. K. A. Gschneidner and F. W. Calderwood, Bull. Alloy Phase Diagrams, 1986, 7, 568–570.
17. M. Atoji and R. H. Flowers, J. Chem. Phys., 1970, 52, 6430–6431.
18. T. E. Weller, M. Ellerby, S. S. Saxena, R. P. Smith and N. T. Skipper, Nat. Phys., 2005, 1, 39–41.
19. G. Csányi, P. B. Littlewood, A. H. Nevidomskyy, C. J. Pickard and B. D. Simons, Nat. Phys., 2005, 10, 1038.
20. I. I. Mazin, Phys. Rev. Lett., 2005, 95, 227001.
21. M. Calandra and F. Mauri, Phys. Rev. Lett., 2005, 95, 237002.
22. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
23. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
24. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
25. I. I. Mazin and S. L. Molodtsov, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 172504.
26. M. Neupane, S. Y. Xu, N. Alidoust, G. Bian, D. J. Kim, C. Liu, I. Belopolski, T. R. Chang, H. T. Jeng and T. Durakiewicz, Phys. Rev. Lett., 2015, 114, 016403.
27. G. Kresse and J. Furthmüler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066.
32. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
33. A. Togo, L. Chaput, I. Tanaka and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174301.
34. T. Mochiku, T. Nakane, H. Kito, H. Takeya, S. Harjo, T. Ishigaki, T. Kamiyama, T. Wada and K. Hirata, Phys. C, 2005, 426–431, 421–425.
35. R. K. Kremer, J. S. Kim, W. H. Xie, V. Babizhetskyy, O. Jepsen, A. Simon, K. S. Ahn, B. Raquet, H. Rakoto and J. M. Broto, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 014516.
36. D. W. Jones, I. J. McColm, R. Steadman and J. Yerkess, J. Solid State Chem., 1984, 53, 376–381.
37. M. Atoji, J. Chem. Phys., 1961, 35, 1950–1960.
38. C. M. Fang, J. Bauer, J. Y. Saillard and J. F. Halet, Z. Naturforsch., 2007, 38, 971–976.
39. F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
40. W. Voigt, Lehrburch der Kristallphysik, Teubner, Leipzig, 1928.
41. A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49.
42. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354.
43. J. Feng, B. Xiao, R. Zhou, W. Pan and D. R. Clarke, Acta Mater., 2012, 60, 3380–3392.
44. X. Gao, Y. Jiang, R. Zhou and J. Feng, J. Alloys Compd., 2014, 587, 819–826.
45. J. P. Watt, J. Appl. Phys., 1986, 60, 3120–3124.
46. J. P. Watt and L. Peselnick, J. Appl. Phys., 1980, 51, 1525–1531.
47. S. F. Pough, Philos. Mag., 1954, 45, 823–843.
48. J. Haines, A. Jm Léger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1–23.
49. P. Ravindran, L. Fast, P. A. Korzhavyi and B. Johansson, J. Appl. Phys., 1998, 84, 4891–4904.
50. J. F. Nye, Physical properties of crystals, Oxford University Press, Oxford, UK, 1985.
51. K. Brugger, J. Appl. Phys., 1965, 36, 768–773.
52. K. Brugger, J. Appl. Phys., 1965, 36, 759–768.
53. J. Feng, B. Xiao, Z. C. Huang, J. C. Chen, C. L. Wan, Z. X. Qu, R. Zhou and W. Pan, Acta Mater., 2010, 72, 1742–1760.
54. B. T. Wang, P. Zhang, R. Lizárraga, I. Di Marco and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 1047.

---