DOI:
10.1039/C5RA22615E
(Paper)
RSC Adv., 2015,
5, 103729-103738
Exploring bridging effect on first hyperpolarizability
Received
28th October 2015
, Accepted 25th November 2015
First published on 26th November 2015
Abstract
A number of tetradehydrodinaphtho[10]annulene derivatives with varying charge transferring conduits between two naphthalene rings have been considered for the theoretical study of electronic structure and first hyperpolarizability. The BHHLYP, CAM-B3LYP and M06-2X methods along with the 6-311++G(d,p) basis set are used to calculate first hyperpolarizability by analytical evaluation of electric dipole second derivative. The results obtained by different methods are found to be consistent. The ground state polarity and the first hyperpolarizability of tetradehydrodinaphtho[10]annulene can be strongly enhanced by suitable modification of acetylene linkages. Using different ring structures containing electronegative atom(s) at the bridging position the extent of the longitudinal charge transfer and the magnitude of first hyperpolarizability can be enhanced strongly. The furan ring and the heteroazulene ring has been found to be the most effective bridging moieties to enhance the magnitude of static first hyperpolarizability. The variation of first hyperpolarizability has been explained satisfactorily in terms of the two state calculated spectroscopic properties.
1. Introduction
Non linear optical (NLO) materials have recently been a major challenging research field because of their potential application in opto electronics, optical computing, dynamic holography, electro-optical, optical switching, optical logic, fluorescence imaging, optical memory, alkali metal cation sensor, optical power limiting and dynamic image processing.1–7 A great deal of research has been devoted to designing various kinds of potential NLO materials the response of which depends on the applied electromagnetic fields of varying frequency, phase etc. The relation between the architecture of a molecule and its non linear response is an important area of research because by understanding the structure–property correlations the NLO property of a material can easily be tuned by selectively varying the structural motif of the molecule.
The use of organic chromophores as NLO materials have significant advantages over the traditional inorganic solids, LiNbO3, KH2PO4, BaTiO3, KTP which exhibit rather poor response property.8 Organic molecules and polymers are promising NLO candidates because of the ease of their structural modifications which help in the efficient design of new molecular systems having high laser damage thresholds, smaller dielectric constant, refractive indices etc. by means of chemical synthetic efforts in conjunction with the computational modelling. The organic molecular species having highly polarizable electronic structure and low-lying charge-transfer excited states, generally, exhibit large NLO coefficients. Most of the second-order NLO-phores, generally have a π-conjugated framework with asymmetrically substituted electron-donor and electron acceptor groups leading to significant longitudinal charge transfer interaction. The NLO property of such molecular systems can be optimized by suitably modifying the structure by introducing donor and acceptor groups9–15 of increasing strength, designing different architecture D–π–A (electron donor–π-bridge–electron acceptor), D–D–π–A (introducing electron donating group as a lateral moiety into the π bridge), D–A–π–A (incorporating additional electron withdrawing moiety into the π bridge as internal acceptor) and also by modifying the π electron system,16 altering bond length parameter,17 modifying charge transfer through space like D–S–A type molecules,18 etc. Doping alkali metal atom in electride system19–21 largely enhances the magnitude of hyperpolarizability. On incorporating different electron deficient and electron rich bridges into the molecular skeleton the intramolecular charge transfer process and the first hyperpolarizability22 can be strongly modulated. Elongated π systems and twisted chromophores are found to exhibit higher first hyperpolarizability.23
In the present work, a number of derivatives of highly delocalized tetradehydrodinaphtho[10]annulene have been considered to find the effect of different bridging conduits on the calculated first hyperpolarizability. The molecule tetrahydrodinaphtho[10]annulene belongs to the sandwich-herringbone type structure exhibiting a π–π stacking interaction.24 The tetradehydrodinaphtho[10]annulene was successfully synthesized, isolated and characterized by Yoshito Tobe25 et al. In the present investigation, we intended to study the effect of structural modification of acetylene bridges of tetradihydronaptho[10]annulene by keeping the same electron donor and electron withdrawing groups at the two ends of naphthalene rings. Our primary concern is to find the precise role of different electronic bridges on the calculated non linear optical properties of tetradehydrodinaphtho[10]annulene derivatives. The present study is expected to reveal a new structure property correlation which will be useful to the experimentalists in the synthetic strategy to design efficient NLO-phores.
2. Computational methods
The ground state geometry of the chosen molecules have been fully optimized at the B3LYP level for the 6-31+G (d,p) basis set. The stability of each structure has been checked by calculating vibrational frequencies of all normal modes at the same level. The calculated frequencies are found to be real which confirm the true minimum in the potential hypersurface. The optimized structures are subsequently used in the calculation of electric response properties. In the presence of external homogeneous electric field of magnitude F0, the induced electric dipole moment of a molecule can be expressed by the following Taylor series expansion| |
 | (1) |
where μ0 is the permanent dipole moment and the coefficients α, β, and γ are called polarizability, first hyperpolarizability and second hyperpolarizability of the molecule, respectively. The vector-part of static dipole first hyperpolarizability (β0) has been calculated by using the following expression,| |
 | (2) |
where βi,s are the components of β vectors lying along the rectangular Cartesian axes. The x-component βx is given by| |
 | (3) |
The components of linear polarizability and first hyperpolarizability of the investigated molecules are evaluated analytically as implemented in Gaussian 09 program.26 The NLO properties are calculated by employing the BHHLYP (50% HF + 50% Becke88 + 50% LSDA exchange and LYP correlation),27 CAM-B3LYP (long range corrected coulombic-attenuating)28 and M06-2X29 functionals for the 6-311++G(d,p) basis set. The BHHLYP and CAM-B3LYP functionals have been used widely for calculation of hyperpolarizabilities. Owing to the lack of experimental and previous theoretical result of hyperpolarizabilities of the investigated molecules, a comparison of the calculated results obtained by the present DFT methods may be useful to find the correct qualitative trend since the magnitude of the calculated hyperpolarizability is generally found to be sensitive to the choice of the DFT functional employed. Among the chosen DFT methods, the CAM-B3LYP functional has been found30,31 to be more reliable for (hyper)polarizability calculation since it can reproduce the results obtained with other correlated ab initio levels. In our previous theoretical work32,33 it has been noted that the use of 6-311++G(d,p) basis set can give nearly identical results of hyperpolarizability as obtained with the Dunning's correlation consistent basis set augmented by higher angular momentum diffuse functions. With regard to the size of the investigated molecules the 6-311++G(d,p) basis set has been considered to be appropriate to obtain reliable results of first hyperpolarizability.
In order to rationalize the variation of static first hyperpolarizability (β) among the chosen molecules the following two state expression34,35 corresponding to the most dominant electronic transition have been invoked.
| |
 | (4) |
The spectroscopic quantities in the above equation are the dipole moment difference (Δμeg), transition energy (ΔEeg) and the oscillator strength [feg =(2me/3ℏ2)μeg2ΔEeg] associated with the electronic transition from the ground state to the predominant charge transfer excited states. The two-state model has been popularly used to optimize10b,36,37 the first-hyperpolarizability of donor–acceptor substituted molecular systems. The spectroscopic parameters Δμeg, feg and ΔEeg are inter-related to each other and are solely controlled by (I) the position and strength of donor and acceptor groups and (II) the nature of the charge transferring bridging moiety.
From the above equation, it seems that the magnitude of first hyperpolarizability should be rather more sensitive to the variation of transition energy compared to the other quantities. The spectroscopic properties of about 20 lowest lying singlet excited states have been calculated by using the time dependent DFT (TDDFT) method consisting of the CAM-B3LYP functional and the 6-311++G(d,p) basis set. The TD-DFT method using the range separated CAM-B3LYP functional can give more accurate results of NLO properties and electronic excitation energies compared to the conventional hybrid functionals.38,39 In order to check the reliability of the TD-CAM-B3LYP method for calculating the spectroscopic quantities for the present molecular system, the λmax value (402 nm) of molecule 1a calculated by using the conductor like polarization continuum model (CPCM) of solvent in the framework of TD CAM-B3LYP/6-311++G(d,p) method for the dichloromethane solvent (ε = 8.93) is compared with the λmax estimated from the UV-VIS spectroscopic result25 obtained in the same solvent. The theoretical result of λmax agrees within 3.5% of the experimental result. Thus the present theoretical results of spectroscopic parameters should be considered reliable.
3. Result and discussion
3.1 Optimized geometrical structures
The optimized ground state structures of tetradehydrodinaphtho[10]annulene and its derivatives are shown in Schemes 1–3. Naphthalene ring substituted with NH2/NO2 groups is denoted as donor naphthalene ring/acceptor naphthalene ring, respectively. Tetradehydrodinaphtho and its derivates having acetylene linker are displayed in Scheme 1. Scheme 2 consists of two five membered rings fused with cyclobutadiene ring (2a and 2b)/furan ring (2c and 2d) as bridging moieties. The structures in Scheme 3 consist of azulene ring (3a and 3b) and heteroazulene ring (with two nitrogen atoms in the larger ring) (3c and 3d) as bridges. In structure 1a the two acetylene moieties deviate from the linearity as indicated by ∠C1C20C19 = 4.9° (Table 1). It is interesting to note that when naphthalene rings are substituted with donor and acceptor groups the bent angle increases by about 0.3° (1b) and 2.8° (1c) with respect to molecule 1a. However, when two consecutive middle carbon atoms of one acetylene moiety are bonded to carbon atoms of parallel acetylene unit forming the fused cyclobutadiene ring as in structures 2a and 2b (Scheme 2) the bent angle becomes larger, ∠C1C20C19 = 161.4° (2a) and ∠C10C11C12 = 160.3° (2b) (Table 1). The corresponding bent angle with fused furan ring increases further, 148.4° (2c) and 148.5° (2d). The dihedral angle between the naphthalene ring and the fused cyclobutadiene ring in molecules 2a (τC9C10C1C20 = 1.9°) and 2b (τC9C10C1C20 = 2.8°) and the same in molecules 2c (0.04°) and 2d (1.9°) indicates that these molecules are nearly planar. However, with azulene ring as the bridging moiety (molecules 3a and 3b) the structures are twisted significantly. As can be seen from Table 1 the two rings of azulene are significantly twisted by 27.9° (3a) and 24.5° (3b). Also the larger ring of azulene fused to the donor naphthalene makes a dihedral angle 19°. However, with heteroazulene ring as a bridging conduit (molecules 3c and 3d, Scheme 3) the structures become almost planar with naphthalene rings on both sides (Table 1).
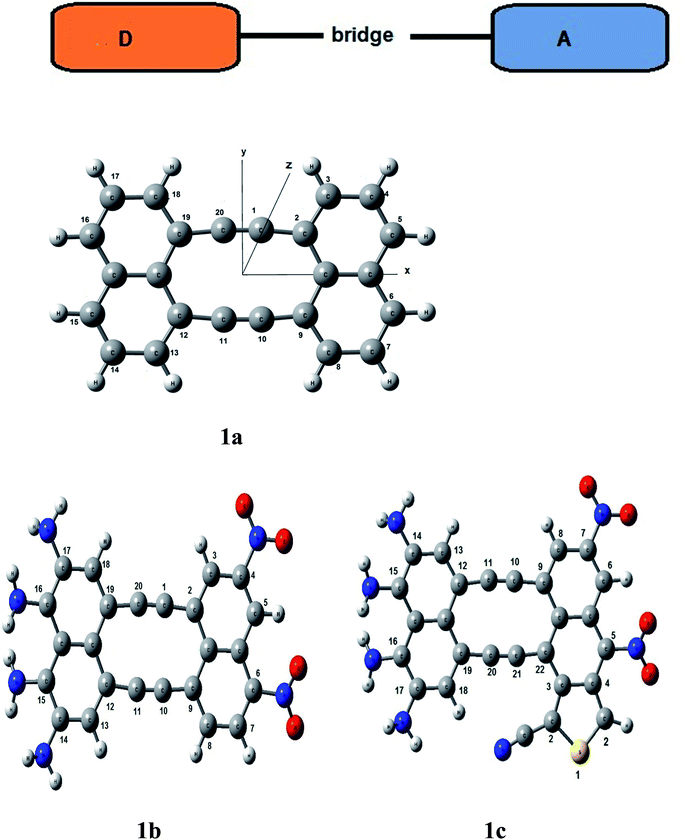 |
| | Scheme 1 Molecules containing acetylene bridging unit. | |
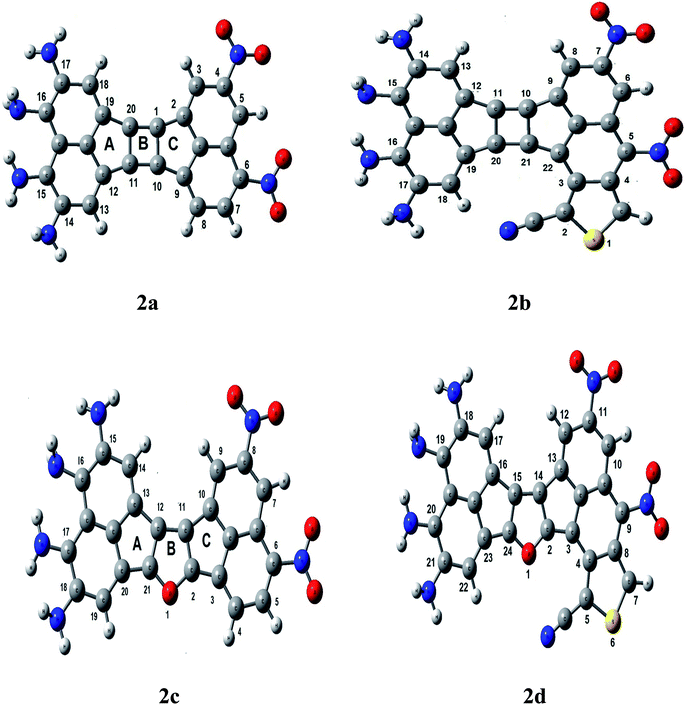 |
| | Scheme 2 Molecules containing cyclobutadiene ring (2a and 2b) and furan ring (2c and 2d) fused with two adjacent cyclo pentadiene rings as bridging units. | |
 |
| | Scheme 3 Molecules containing azulene ring (3a and 3b) and heteroazulene ring (3c and 3d) as bridging units. | |
Table 1 Important bond angles and torsion angles (in degree) of molecules of Schemes 1–3
| Schemes 1 and 2 |
| Molecules |
Angle |
Molecules |
Angle |
| ∠C1C20C19 |
∠C10C11C12 |
| 1a |
175.1 |
1c |
172.3 |
| 1b |
174.8 |
2b |
160.3 |
| 2a |
161.4 |
|
|
| |
∠C11C12C13 |
|
∠C14C15C16 |
| 2c |
148.4 |
2d |
148.6 |
| Scheme 3 |
| Molecules |
τC9C10C1C20 |
Molecules |
τC22C21C10C11 |
| 3a |
27.9 |
3b |
24.5 |
| 3c |
1.4 |
3c |
1.3 |
Let us now find whether the greater bent angle in molecules 2c (vs. 2a) and 2d (vs. 2b) will have any effect on the polarity of the bridging moiety. For this purpose, we compare the electron density distribution at the bridging position of molecules 2a and 2c (Scheme 2). The three segments of the bridge possess NBO charges: +0.126 (A), +0.442 (B) and −1.029 (C) for molecule 2a; −0.676 (A), −0.227 (B) and −0.359 (C) for molecule 2c. This indicates that the extent of longitudinal electron transfer segment A → segment C in 2a enhances significantly while it reduces substantially in molecule 2c. The relatively larger electron population in part A compared to regions B and C of molecule 2c opposes the longitudinal charge transfer which has been reflected by the smaller ground state dipole moment (12.3 D) and larger LUMO–HOMO energy gap (0.064 au) compared to that (19.2 D and 0.060 au) of molecule 2a. Designating the donor substituted naphthalene ring as E and acceptor substituted naphthalene ring as F it has been noted that charge transfer from ring E (+0.230) is much larger with heteroazulene bridge (3c) compared to that (+0.054) with the azulene bridge (3a). This is fairly consistent with the greater accumulation of negative charge in the naphthalene ring F with heteroazulene bridge (−2.116) in contrast to the azulene bridge (−0.622). The greater amount of E → F charge transfer across the heteroazulene bridge is due to the perfect planarity of the later in contrast to the azulene bridge in which case the two rings are twisted. This has been reflected in the NBO calculated net charge on the larger/smaller ring, −0.297/−0.372 (heteroazulene) vs. −0.594/−0.105 (azulene) although the net charge density on each of the bridging moiety is almost equal.
As discussed above the nature of charge transfer interaction of the investigated molecules has been significantly modulated due to the difference of electronic structure of the bridging units. The calculated frontier orbital interaction energy can provide an additional insight. Generally, the energy of a HOMO (LUMO) of a conjugated hydrocarbon increase (decrease) when an electron donor (acceptor) attaches to it. For a given bridge the acceptor strength increases by incorporating the cyano substituted thiophene ring which results in the substantial lowering of LUMO–HOMO energy gap (au) (1c (0.054) vs. 1b (0.072); 2b (0.051) vs. 2a (0.060); 2d (0.048) vs. 2c (0.064); 3b (0.061) vs. 3a (0.076); 3d (0.046) vs. 3c (0.061)).
3.2 Static first hyperpolarizability
For the chosen molecules the prominent charge transfer interaction takes place along the x axis which is reflected in the magnitude of ground state dipole moment (μg) that is almost identical to the x-component (μx). Thus this axial component of polarizability and first hyperpolarizability is taken as the longitudinal component. This is evident from the nearly identical magnitudes of βx and β0 (Tables 2–4). The calculated results of ground state dipole moment and first hyperpolarizability obtained by different DFT methods (BHHLYP, CAM-B3LYP and M062X) are compared in Tables 2–4. The ground state dipole moment obtained by different methods differs by a narrow margin. By attaching electron donor and acceptor groups at the terminal sites of naphthalene rings of molecule 1a the dipole moment can be strongly enhanced (1a < 1c < 1b). The introduction of furan ring at the bridge substantially lowers the μg value when compared to the cyclobutadiene ring (2c < 2a and 2d < 2b). The larger ground state dipole moment of molecules 3a and 3b compared to molecules 3c and 3d, respectively may be due to the twisted structure of azulene. For the chosen molecules the CAM-B3LYP results of β0 differs from the M06-2X results by about 0.4–6.4% except for molecule 2b and 1a. The M06-2X β0 value of the later compared to CAM-B3LYP value is underestimated by about 11.7%. At the BHHLYP level β0 value of molecule 2a is substantially underestimated in comparison to the CAM-B3LYP and M06-2X results. The results of first hyperpolarizability of the chosen molecules calculated by three DFT methods are compared in Fig. 1. It can be seen that although β0 value of a molecule differs at the three levels the general trend remains same. The three methods identically predict the highest magnitude of first hyperpolarizability for each scheme which varies in the order 1c (Scheme 1) < 2d (Scheme 2) < 3d (Scheme 3). It should be noted that for molecules 1c and 2d the M06-2X calculated β0 is smaller than the CAM-B3LYP results by about 2%. On the other hand the BHHLYP and M06-2X calculated β0 values obtained for molecule 3d are underestimated significantly (by 10.4% and 6.4%) compared to the CAM-B3LYP results. However, the BHHLYP β0 and M06-2X β0 of this molecule agree within 4.0%.
Table 2 Ground state dipole moment (μ, debye) and first hyperpolarizability (β, au) of molecules of Scheme 1 obtained at different DFT functionals for the 6-311++G(d,p) basis set
| |
|
1a |
1b |
1c |
| BHHLYP |
μx |
0.000 |
14.929 |
14.369 |
| μg |
0.000 |
15.199 |
14.698 |
| βx |
0.3 |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424.6 424.6 |
125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882.0 882.0 |
| β0 |
0.4 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047.0 047.0 |
127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164.0 164.0 |
| CAM-B3LYP |
μx |
0.000 |
14.517 |
13.854 |
| μg |
0.000 |
14.771 |
14.187 |
| βx |
0.3 |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727.5 727.5 |
138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 453.0 453.0 |
| β0 |
0.4 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304.0 304.0 |
139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658.0 658.0 |
| M06-2X |
μx |
0.000 |
14.675 |
13.972 |
| μg |
0.000 |
14.929 |
14.340 |
| βx |
0.323 |
80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458.4 458.4 |
135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.0 520.0 |
| β0 |
0.3 |
81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013.0 013.0 |
136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657.5 657.5 |
Table 3 Ground state dipole moment (μ, debye) and first hyperpolarizability (β, au) of molecules of Scheme 2 obtained at different DFT functionals for the 6-311++G(d,p) basis set
| |
|
2a |
2b |
2c |
2d |
| BHHLYP |
μx |
19.735 |
23.975 |
12.769 |
−13.761 |
| μg |
19.755 |
23.975 |
12.923 |
13.895 |
| βx |
−50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 546.4 546.4 |
63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896.3 896.3 |
−118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584.0 584.0 |
183![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839.0 839.0 |
| β0 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654.5 654.5 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364.0 364.0 |
118![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838.0 838.0 |
184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087.5 087.5 |
| CAM-B3LYP |
μx |
19.158 |
23.573 |
12.180 |
−12.789 |
| μg |
19.177 |
23.586 |
12.323 |
12.919 |
| βx |
−59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925.5 925.5 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649.1 649.1 |
−108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521.0 521.0 |
208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766.0 766.0 |
| β0 |
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123.5 123.5 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135.0 135.0 |
108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811.0 811.0 |
208![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.0 972.0 |
| M06-2X |
μx |
19.240 |
23.394 |
12.350 |
−12.911 |
| μg |
19.261 |
23.415 |
12.495 |
13.067 |
| βx |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962.9 962.9 |
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.7 664.7 |
−110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796.0 796.0 |
204![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638.0 638.0 |
| β0 |
59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.0 157.0 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910.5 910.5 |
111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097.0 097.0 |
204![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864.0 864.0 |
Table 4 Ground state dipole moment (μ, debye) and first hyperpolarizability (β, au) of molecules of Scheme 3 obtained at different DFT functionals for the 6-311++G(d,p) basis set
| |
|
3a |
3b |
3c |
3d |
| BHHLYP |
μx |
−18.371 |
−16.187 |
13.490 |
13.205 |
| μg |
18.533 |
16.493 |
13.793 |
13.497 |
| βx |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422.7 422.7 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628.5 628.5 |
−110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809.0 809.0 |
−189![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.0 212.0 |
| β0 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640.3 640.3 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733.6 733.6 |
111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 497.0 497.0 |
190![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597.0 597.0 |
| CAM-B3LYP |
μx |
17.902 |
−15.815 |
13.089 |
12.476 |
| μg |
18.058 |
16.117 |
13.378 |
12.783 |
| βx |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921.5 921.5 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885.3 885.3 |
−102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668.0 668.0 |
−211![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412.0 412.0 |
| β0 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153.8 153.8 |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052.0 052.0 |
103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 259.0 259.0 |
212![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679.0 679.0 |
| M06-2X |
μx |
−17.779 |
−15.744 |
13.361 |
12.810 |
| μg |
17.942 |
16.086 |
13.644 |
13.144 |
| βx |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051.1 051.1 |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 022.6 022.6 |
−105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788.0 788.0 |
−197![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779.0 779.0 |
| β0 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287.9 287.9 |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271.5 271.5 |
106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385.5 385.5 |
199![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 018.5 018.5 |
 |
| | Fig. 1 The variation of first hyperpolarizability among molecules of Schemes 1–3. | |
3.3 Structural effect on first hyperpolarizability and TDDFT analysis
It will be interesting to find the effect of change of bridging conduit on the calculated first hyperpolarizability. As it has been discussed in last subsection that for an identically substituted naphthalene rings the modification of electronic structure of the bridge moiety leads to the significant modulation of the charge distribution and hence the polarity of the ground state structure. However, for the same bridge the presence of cyano substituted fused thiophene ring strongly enhances the magnitude of first hyperpolarizability when compared with molecules without the thiophene moiety. In molecules 2a and 2b the cyclobutadiene ring and for molecules 2c and 2d furan ring imparts rigidity to the bridging moiety. However, the larger ground state dipole moment of molecules 2a and 2b results in significant lowering of β0 value compared to molecules 1b and 1c, respectively. The β0 of molecule 2a enhances by about 14.2% (CAM-B3LYP) when a thiophene ring bearing a –CN group is fused with the acceptor naphthalene ring (molecule 2b). On the other hand the incorporation of furan ring in the bridge (molecules 2c and 2d) substantially lowers the ground state dipole moment but enhances β0 by about an order of magnitude when compared to molecules 2a and 2b.
We next consider the effect of azulene bridge (molecules 3a and 3b) on the NLO property. Owing to the loss of planarity of the azulene ring the longitudinal charge transfer is strongly hindered which results in substantial lowering of first hyperpolarizability. It would be worthwhile to compare the structural changes of the bridging unit on the first hyperpolarizability of molecules 1c, 2b and 3b. On going from 1c to 2b the bent angle increases which probably causes a significant lowering of β0 value of 2b. However, the loss of planarity of the bridge in molecule 3b dramatically reduces the magnitude of β0. On the other hand when hetero-azulene ring has been used as a bridge (molecules 3c and 3d) the perfect planarity is maintained between the naphthalene rings. As a result the extent of charge transfer is markedly enhanced leading to rather strong enhancement of β0 by about 3.4 times (3c vs. 3a) and 4.2 times (3d vs. 3b). The exceptionally large increase of quadratic polarizability of molecules 3c and 3d also arises from the significant charge transfer from the larger ring to the smaller ring. The most effective role of π bridge on the second order NLO property can be found for molecules 1b, 2c and 3c which have planar structures but the ring structures of the bridge of molecules 2c and 3c play a more crucial role in the modulation of longitudinal charge transfer. The NBO calculated results of charge on the acetylene bridge (−0.085), the three rings of molecule 2c (−0.676 (A), −0.227 (B) and −0.359 (C)) and that of molecule 3c (−0.297 and −0.372 on the larger and smaller rings of heteroazulene, respectively) indicates that the excess negative charge density on ring A of molecule 2c will favour energetically the linear transition in comparison to molecules 1b and 3c. This has been reflected in the larger first hyperpolarizability of molecule 2c. The variation of β0 is fairly consistent with the bridge atomic charge sum (BACS)40 of the molecules.
The TD-CAMB3LYP calculated results of spectroscopic properties along with the two state (eqn (4)) calculated values of first hyperpolarizability obtained for the investigated molecules are presented in Table 5. The two-state model has been invoked to explain the variation of first hyperpolarizability (β0) of the chosen molecules. According to this model the magnitude of first hyperpolarizability is directly proportional to the dipole moment (Δμeg) difference between the excited and ground state, and the oscillator strength (feg) but inversely proportional to the third power of transition energy (ΔEeg) associated with the crucial electronic transition. The frontier orbital plots are shown in Fig. 2. For molecules of Scheme 1 the increase of β0 in the order 1a < 1b < 1c is fairly consistent with the gradual lowering of transition energy and increase of transition moment. The HOMO is mostly concentrated on donor naphthalene ring and LUMO is concentrated on acceptor ring which accounts for the larger transition moment of molecules 1b and 1c. The large decrease of first hyperpolarizability of molecule 2a compared to that of 1b arises primarily from the significantly smaller dipole moment difference (0.785 au) of the former compared to that (3.586 au) of the later. The substantially smaller Δμeg value of molecule 2a is explained by the fact that the partly delocalised π electrons in the cyclobutadiene ring do not take part in the longitudinal charge transfer which has been reflected in the HOMO–LUMO pictures of 2a. The rather smaller β0 (by an order of magnitude) of 2b compared to its valence isomer 1c has been attributed to the smaller transition moment (oscillator strength) and dipole moment difference of 2b. The presence of furan ring (molecule 2c, Scheme 2) increases the dipole moment difference term (Δμeg) rather appreciably when compared to molecule 2a. This spectroscopic quantity alone can account for the significant enhancement of first hyperpolarizability of molecule 2c. The distribution of orbital lobes of HOMO and LUMO of molecule 2c clearly indicates that significant amount of electron transfer occurs upon electronic excitation from regions A and B to C of the molecule (Scheme 2). When the acceptor side of molecule 2c is further modified by attaching a cyano substituted thiophene ring (molecule 2d), the β0 value increases by almost 47.9% (CAM-B3LYP level). The rather strong enhancement of quadratic polarizability of molecule 2d compared to 2c originates from the substantial lowering of ΔEeg value of the former. This is fairly consistent with the two-level calculated results of β0.
Table 5 Transition energy (ΔEeg, au), transition moment (μeg, D), dipole moment difference (Δμeg, au), oscillator strength (feg, au) and two state calculated first hyperpolarizability (β0, au) corresponding to the most intense electronic transition (S0 → Sn) obtained at the CAM-B3LYP level for the 6-311++G(d,p) basis set
| Molecule |
ΔEeg |
μeg |
Δμeg |
feg |
β0 |
Electronic transition |
Orbital transition |
| 1a |
0.11729 |
7.923 |
0.000 |
0.755 |
0.18 |
S0 → S1 |
HOMO → LUMO |
| 1b |
0.08854 |
9.179 |
3.586 |
0.765 |
3952.33 |
S0 → S1 |
HOMO → LUMO |
| 1c |
0.06179 |
9.866 |
1.662 |
0.616 |
4338.64 |
S0 → S1 |
HOMO → LUMO |
| 2a |
0.07067 |
9.710 |
0.785 |
0.683 |
1518.75 |
S0 → S2 |
HOMO → LUMO |
| 2b |
0.05728 |
8.437 |
1.268 |
0.418 |
2820.43 |
S0 → S2 |
HOMO → LUMO |
| 2c |
0.07492 |
6.883 |
4.309 |
0.364 |
3729.26 |
S0 → S1 |
HOMO → LUMO |
| 2d |
0.04954 |
8.858 |
1.806 |
0.398 |
5911.65 |
S0 → S1 |
HOMO → LUMO |
| 3a |
0.10941 |
6.235 |
1.044 |
0.436 |
347.62 |
S0 → S7 |
HOMO → LUMO |
| 3b |
0.07340 |
5.935 |
1.335 |
0.265 |
894.90 |
S0 → S4 |
HOMO → LUMO+1 |
| 3c |
0.08625 |
7.507 |
4.679 |
0.498 |
3632.08 |
S0 → S2 |
HOMO → LUMO |
| 3d |
0.05191 |
8.145 |
2.129 |
0.353 |
5373.14 |
S0 → S1 |
HOMO → LUMO |
 |
| | Fig. 2 The frontier orbital pictures of some representative molecules of Schemes 1–3. | |
Let us now discuss the effect of azulene bridge on the magnitude of first hyperpolarizability. The loss of planarity between the two rings of azulene and also between the larger ring of azulene and the donor naphthalene ring strongly hinders the extent of longitudinal charge transfer in molecules 3a and 3b which results in substantially higher ΔEeg and smaller Δμeg values in comparison to molecules 3c and 3d having planar structures. The higher β0 of 1c compared to that of molecules 2b and 3b can be attributed to the higher Δμeg and feg values of the former. However, the higher β0 of 2b than 3b arises mainly from the substantial lowering of ΔEeg value of 2b. The significant lowering of ΔEeg of molecule 2c compared to 1b and 3c leads to strong enhancement of β0 of the former. The relative variation of above spectroscopic parameters reasonably accounts for the strong enhancement of β0 (by an order) of molecules 3c (versus 3a) and 3d (versus 3b). The substantially larger Δμeg value of molecule 3c compared to 3a arises from the enhanced longitudinal charge transfer in the former which has been reflected in the HOMO–LUMO pictures (Fig. 2). The decrease of charge transfer interaction in molecule 3a is also consistent with the frontier orbital pictures exhibiting a greater accumulation of charge density on the azulene because of its twisted structure. The significantly larger quadratic polarizability of molecule 3d than that of 3c is attributed to the significant lowering of HOMO to LUMO transition energy gap.
4. Conclusion
In the present study, a number of different derivatives of tetradehydrodinaphtho[10]annulene have been considered for the theoretical study of the electronic structure and first hyperpolarizability by employing BHHLYP, CAM-B3LYP and M06-2X functionals. The CAM-B3LYP and M06-2X calculated results, in general, are found to agree within a close margin. Our theoretical study demonstrates that the partial modification of acetylene linkages between two naphthalene rings may lead to significant modulation of longitudinal charge transfer and polarity at the ground state which in turn predicts a dramatic variation of first hyperpolarizability. The electronic nature and planarity of the bridging moiety play a crucial role in the modulation of opto electronic property of the investigated molecules. The heterocyclic ring moieties at the bridge position in conjunction with the acceptor substituted thiophene ring fused with the naphthalene ring at the acceptor side are found to predict significantly large first hyperpolarizability. The variation of first hyperpolarizability has been explained satisfactorily in the light of two state model.
Acknowledgements
(RSR) acknowledges the UGC BSR (F.7-223/2009 (BSR)) for financial support and (PKN) acknowledges the grant from UGC, Government of India under the Major Research Project (F. No. 42-339/2013 (SR)) for carrying out this research work.
References
- J. M. Squirrell, D. L. Wokosin, J. G. White and B. D. Bavister, Nat. Biotechnol., 1999, 17, 763–767 CrossRef CAS PubMed.
- Y. H. Jiang, Y. C. Wang, J. B. Yang, J. L. Hua, B. Wang, S. Q. Qian and H. Tian, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 1830 CrossRef CAS.
- D. R. Kanis, M. N. Ratner and T. Marks, Chem. Rev., 1994, 94, 195 CrossRef CAS.
- D. Bella, Chem. Soc. Rev., 2001, 30, 355–366 RSC.
-
(a) D. S. Chemla and J. Zyss, Nonlinear Optical Properties of Organic Molecules and Crystals, Academic Press, New York, 1987, vol. 1 Search PubMed;
(b) C. W. Spangler, J. Mater. Chem., 1999, 9, 2013–2020 RSC;
(c) Y. Gao, S. L. Sun, H. L. Xu, L. Zhao and Z. M. Su, RSC Adv., 2014, 4, 24433–24438 RSC.
- D. J. Williams, Nonlinear Optical Properties of Organic and Polymer Materials, American Chemical Society, Washington, DC, 1985, ACS Symposium Series 233 Search PubMed.
- P. R. Prasad and D. J. Williams, Introduction to Non-linear Optical Effects in Molecules and Polymers, Wiley, New York, 1991 Search PubMed.
- R. A. Hann and D. Bloor, Organic Materials for Nonlinear Optics, Royal Society of Chemistry, London, 1989 Search PubMed.
- L. R. Dalton, A. W. Harper, R. Ghosn, W. H. Steier, M. Ziari, H. Fetterman, Y. Shi, R. V. Mustacich, A. K. Y. Jen and K. J. Shea, Chem. Mater., 1995, 7, 1060 CrossRef CAS.
-
(a) L. T. Chen, W. Tam, S. R. Marder, A. E. Stiegman, G. Rikken and C. W. Spangler, J. Phys. Chem., 1991, 95, 10643 CrossRef;
(b) S. R. Marder, D. N. Beratan and L.-T. Cheng, Science, 1991, 252, 103–106 CAS.
- C. M. Whitaker, E. V. Patterson, K. L. Kott and R. J. McMahon, J. Am. Chem. Soc., 1996, 118, 9966–9973 CrossRef CAS.
- P. K. Nandi, N. Panja and T. K. Ghanty, J. Phys. Chem. A, 2008, 112, 4844–4852 CrossRef CAS PubMed.
- P. K. Nandi, N. Panja and T. K. Ghanty, J. Phys. Chem. A, 2009, 113, 2623–2631 CrossRef CAS PubMed.
- P. K. Nandi, N. Panja and T. K. Ghanty, Theor. Chem. Acc., 2010, 126, 323–337 CrossRef.
- K. Hatua and P. K. Nandi, J. Theor. Comput. Chem., 2013, 12, 1250099 CrossRef.
-
(a) F. Liu, Y. Yang, S. Cong, H. Wang, M. Zhang, S. Bo, J. Liu, Z. Zhen, X. Liu and L. Qiu, RSC Adv., 2014, 4, 52991–52999 RSC;
(b) S. R. Marder, C. B. Gorman, F. Meyers, J. W. Perry, G. Bourhill, J. L. Bredas and B. M. Pierce, Science, 1994, 265, 632–635 CAS.
- F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS.
- X. Zhang, H. Q. Wu, H. L. Xu, S. L. Sun and Z. M. Su, J. Phys. Chem. A, 2015, 119, 767–773 CrossRef CAS PubMed.
- A. S. Ichimura, J. L. Dye, M. A. Camblor and L. A. Villaescusa, J. Am. Chem. Soc., 2002, 124, 1170–1171 CrossRef CAS PubMed.
- W. Chen, Z. R. Li, D. Wu, Y. Li, C. C. Sun and F. L. Gu, J. Am. Chem. Soc., 2005, 127, 10977–10981 CrossRef CAS PubMed.
- S. Muhammad, H. L. Cut, Y. Liao, Y. H. Kan and Z. M. Su, J. Am. Chem. Soc., 2009, 131, 11833–11840 CrossRef CAS PubMed.
-
(a) H. Xu, D. Yang, F. Liu, M. Fu, S. Bo, X. Liu and Y. Cao, Phys. Chem. Chem. Phys., 2015, 17, 29679–29688 RSC;
(b) I. D. L. Albert, T. J. Marks and M. A. Ratner, J. Am. Chem. Soc., 1997, 119, 3155–3156 CrossRef CAS;
(c) I. D. L. Albert, T. J. Marks and M. A. Ratner, Chem. Mater., 1998, 10, 753–762 CrossRef CAS;
(d) P. R. Varanasi, A. K. Y. Jen, J. Chandrasekhar, I. N. N. Namboothiri and A. Rathna, J. Am. Chem. Soc., 1996, 118, 12443–12448 CrossRef.
- Y. Shi, D. Frattarelli, N. Watanabe, A. Facchetti, E. Cariati, S. Righetto, E. Tordin, C. Zuccaccia, A. Macchioni, S. L. Wegener, C. L. Stern, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2015, 137, 12521–12538 CrossRef CAS PubMed.
-
(a) G. R. Desiraju and A. Gavezzotti, J. Chem. Soc., Chem. Commun., 1989, 621–623 RSC;
(b) A. Gavezzotti and G. R. Desiraju, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 427–434 CrossRef.
- R. Umeda, D. Hibi, K. Miki and Y. Tobe, Org. Lett., 2009, 11, 4104 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- G. E. Hohenstein, T. S. Chill and D. C. Sherrill, J. Chem. Theory Comput., 2008, 4, 1996–2000 CrossRef.
- P. A. Limacher, K. V. Mikkelsen and H. P. Lüthi, J. Chem. Phys., 2009, 130, 194114 CrossRef PubMed.
- A. Alparone, Chem. Phys. Lett., 2011, 514, 21–25 CrossRef CAS.
- K. Hatua and P. K. Nandi, J. Phys. Chem. A, 2013, 117, 12581–12589 CrossRef CAS PubMed.
- K. Hatua and P. K. Nandi, J. Mol. Model., 2014, 20, 2440 CrossRef PubMed.
- J. L. Oudar, J. Chem. Phys., 1977, 67, 446 CrossRef CAS.
- J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664 CrossRef CAS.
- R. Sen, D. Majumdar, S. P. Bhattacharyya and S. N. Bhattacharyya, J. Phys. Chem., 1993, 97, 7491 CrossRef CAS.
- M. Barzoukas, C. Runser, A. Fort and B. M. Desce, Chem. Phys. Lett., 1996, 257, 531 CrossRef CAS.
- M. J. G. Peach, T. Helgaker, P. Salek, T. W. Keal, O. B. Lutnæs, D. J. Tozer and N.
C. Handy, Phys. Chem. Chem. Phys., 2006, 8, 558–562 RSC.
- B. M. Wong and T. H. Hsieh, J. Chem. Theory Comput., 2010, 6, 3704–3712 CrossRef CAS PubMed.
- W. Zhu and Y. Jiang, Phys. Chem. Chem. Phys., 1999, 1, 4169–4173 RSC.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 

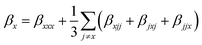



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424.6
424.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 882.0
882.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047.0
047.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164.0
164.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727.5
727.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 453.0
453.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304.0
304.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 658.0
658.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458.4
458.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520.0
520.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013.0
013.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657.5
657.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 546.4
546.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896.3
896.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584.0
584.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 839.0
839.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 654.5
654.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364.0
364.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 838.0
838.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087.5
087.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925.5
925.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 649.1
649.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521.0
521.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766.0
766.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 123.5
123.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135.0
135.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811.0
811.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.0
972.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962.9
962.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664.7
664.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796.0
796.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638.0
638.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.0
157.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910.5
910.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097.0
097.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864.0
864.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422.7
422.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 628.5
628.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 809.0
809.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.0
212.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640.3
640.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733.6
733.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 497.0
497.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 597.0
597.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921.5
921.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885.3
885.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668.0
668.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412.0
412.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153.8
153.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052.0
052.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 259.0
259.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679.0
679.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051.1
051.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 022.6
022.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 788.0
788.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779.0
779.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287.9
287.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271.5
271.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385.5
385.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 018.5
018.5


