Pressure-induced structural changes and elemental dissociation of cadmium and mercury chalcogenides

Abstract

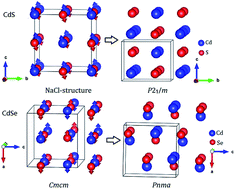
Cadmium and mercury chalcogenide compounds have broad applications (e.g. in light-emitting diodes, chemical sensors, and solar cells). Pressure has profound effects on their structures and properties. However, their structures and phase transition sequences under pressure have not been fully determined, which greatly hinders their further applications. Here, we have extensively explored the high-pressure structures of cadmium and mercury chalcogenides (CdX, HgX, X = S, Se and Te) by using the in-house developed CALYPSO method. The results show that their high-pressure structures and phase transition sequences strongly correlate with the chalcogens. An intriguing dissociation into Cd (or Hg) + X under strong compression was observed. This observation might originate from the special sandwich structure, which significantly frustrates Cd (or Hg)–X bonding and enhances the interaction of the same kind of atoms. Moreover, the dissociation pressures of cadmium and mercury chalcogenides decrease with increasing the atomic radius of the chalcogens. The high-pressure decomposition of cadmium and mercury chalcogenides might have important implications for other binary compounds.

---

1. Introduction

The main aim of high-pressure research is to explore the structural behaviours of the concerned materials and find their potential technological applications. Under high pressure, new crystal phases appear, which are not only beyond the naturally occurring forms but also associated with interesting physical and chemical properties.^1–7 The group IIB-VIA binary compounds have attracted significant interest owing to their broad applications, such as light-emitting diodes, field-effect transistors, chemical sensors, catalysis, and solar cells.^8–11 In addition, the high-pressure behaviour of group IIB-VIA binary compounds has been explored in the past 30 years.^12–15 By now, the generally accepted transition sequence for IIB-VIA compounds was zinc-blended (ZB) or wurtzite (WZ) → NaCl → Cmcm.^16,17 Moreover, there are significant differences in the electronic properties among these phases (i.e. semiconductor, insulator, and metal). The NaCl → Cmcm transition is attributed to the softening of the transverse acoustic TA(X) phonon of the NaCl phase with increasing pressure. Meanwhile, the coordination number is changed from 4 to 8 upon the phase transition process.¹⁸

Compared with zinc chalcogenides, cadmium and mercury chalcogenides (denoted as CdX, and HgX, X = S, Se and Te) are also important technological materials, especially in optoelectronic materials.^19,20 Under compression, although the transition sequence of the cadmium and mercury chalcogenides is similar to that of zinc chalcogenides, there are some differences between them. For example, the NaCl phase is preceded by a cinnabar phase in the mercury chalcogenides, which is donated as a distorted rocksalt phase.²¹ Moreover, a controversial CsCl structure has been considered as a candidate for very large compression on account of its low Madelung energy, which still needs to be confirmed. For CdTe and HgS, the post-NaCl phase has been reported by Nelmes and McMahon at 42 and 52 GPa, however, the structures of these high-pressure phases remain unresolved so far.¹⁶ For the zinc chalcogenides, an intriguing dissociation into Zn + X under strong compression was found,²¹ how about the stability of the cadmium and mercury chalcogenides under strong compression is still unknown. By all appearance, there is a necessity to examine the phase transitions and stabilities of the cadmium and mercury chalcogenides under pressures.

In this work, we have performed a systematic study on the high-pressure structural behaviours of the cadmium and mercury chalcogenides by using the in-house developed unbiased structure searching techniques and first-principles density functional calculations. Beyond the Cmcm phase, we found a monoclinic P2₁/m phase and a tetragonal structure (P4/nmm, Z = 2) for CdS at 70 GPa and 100 GPa, respectively. Moreover, we have also unraveled an orthorhombic Pnma structure for CdSe and a metastable hexagonal structure (P3̄m1, Z = 4) for CdTe at 80 GPa and 55 GPa, respectively. For CdS and CdSe, phase transition to a PbO-type structure (P4/nmm, Z = 2) is a common tendency, while a monoclinic phase (C2/m, Z = 4) was identified for HgS as a post-NaCl phase at 57 GPa. Interestingly, the pressure-induced elemental dissociation has been found for cadmium and mercury chalcogenides, which might have important implications for the behaviours of other binary compounds under high pressures.

2. Computational methods

To search the possible high-pressure structures, we used the CALYPSO structure prediction method^22,23 based on a particle swarm optimization algorithm in combination with ab initio density functional theory (DFT) total-energy calculations. The most significant feature of this methodology is the capability of predicting the stable structure with only the knowledge of the chemical composition. The details of this search algorithm and its several applications have been described elsewhere.^22,23 This approach has successfully predicted the crystal structures of a diverse variety of materials.^24–27 We perform structure searching with simulation cell sizes of 1–4 formula units at pressure of 0, 25, 50, 100, 150, and 200 GPa, respectively. The underlying ab initio structural relaxations were performed using density functional theory within the generalized gradient approximation,²⁸ as implemented in the VASP (Vienna ab initio Simulation Package) code.²⁹ The electron–ion interaction was described by means of the frozen-core all-electron projector-augmented wave method,³⁰ with Cd 4d¹⁰5s², Hg 5d¹⁰6s², S 3s²3p⁴, Se 4s²4p⁴, and Te 5s²5p⁴ treated as the valence electrons, respectively. The use of a plane-wave kinetic energy cutoff of 400 eV for all cases and dense k-point sampling were chosen to ensure that all the enthalpy calculations were well converged to less than 1 meV per atom. Phonon frequencies were calculated using direct supercell, which uses the forces obtained by the Hellmann–Feynman theorem, as performed in phonopy code.^31,32

3. Results and discussion

3.1 Cadmium chalcogenides

Our swarm-intelligence CALYPSO simulations successfully reproduced the NaCl phase for CdS at 50 GPa and Cmcm structure for CdSe at 45 GPa, respectively. Thus, the adopted methods and pseudopotentials are suitable to the studied compounds. At 59 GPa, we revealed a monoclinic structure with space group P2₁/m as the most stable post-NaCl phase for CdS, which is in sharp contrast to the proposed Cmcm structure.^33,34 Above 100 GPa, our structural prediction uncovered a new high-pressure PbO-type phase with tetragonal P4/nmm (Z = 2) to be most stable. Interestingly, we also find another tetragonal structure with same space group, however, which contains 4 formula units (Z = 4). Its enthalpy is higher than that of P4/nmm (Z = 2) at low-pressure region. Detail structural differences between the two structures will be discussed later. It is noted that cadmium chalcogenides tends to decompose into the elemental solids at strong compression (Fig. 1).

Fig. 1 Calculated enthalpy curves versus pressure for the various CdX structures and decomposition into Cd + X relative to the NaCl phase for CdS, Cmcm phase for CdSe, and Cmcm phase for CdTe, respectively.

For IIB-VIA compounds, NaCl-type structure usually transforms to Cmcm phase under pressure.^35,36 However, P2₁/m structure for CdS becomes energetically more favourable than the Cmcm structure. To understand this interesting transition mechanism, we further explored the dynamical stability of NaCl-type structure and pressure-driven phonon softening. If the shear distortion of NaCl-type structure favors [010] direction, Cmcm phase will be most stable.³⁵ Instead, if the true energy minimum lies in distortion path along some directions between [010] and [110], this will result in a lower-symmetry P2₁/m phase.^21,34 The specific structural phase transition mechanism of NaCl → P2₁/m has been revealed by the analysis of TA(X) phonon softening in NaCl (Fig. 2b). From the phonon dispersion curves of CdS in the NaCl structure (Fig. 2a), we see that the frequencies of the TA(X) mode along some direction between [010] and [110] decrease with increasing pressure. This decrease implies negative Grüneisen parameters of the TA mode in the NaCl structure. With increasing pressure, the frequency of this branch becomes imaginary at the zone boundary X point, as can be seen in Fig. 2a, denoting a structural instability of the NaCl phase. Through the analysis of the phonon eigenvectors, we found that the formation of the P2₁/m structure can actually be attributed to a distortion of the NaCl phase that comes from the detachment of the anions and cations from the same plane driven by the soft TA phonon mode at the X point, as shown in Fig. 2b. The energy evolution curve along the eigenvector direction between [010] and [110] also supports this conclusion (Fig. S1†). It should be also pointed out that the predicted TA(X) mode softening in CdS has also been observed in the other binary compounds with NaCl structure.^33–38 Furthermore, dynamic stability for P2₁/m phase was investigated by inspecting phonon dispersive curves in Fig. 2e. No imaginary frequency was found for P2₁/m phase, indicating that it is dynamically stable. Its optimized lattice parameters are a = 3.26 Å, b = 4.61 Å, c = 3.68 Å and β = 89.96° at 70 GPa. The atomic coordinates were as follows: S (0.368, 0.75, 0.251) and Cd (0.112, 0.25, 0.249).

Fig. 2 (a) The phonon dispersive curves for the NaCl phase of CdS at 80 GPa. (b) Conventional cell of the NaCl phase with the eigenvector of the unstable TA(X) mode indicated by arrows. The arrows show the directions of atomic displacements. (c) The phonon dispersive curves for Cmcm structure of CdSe at 50 GPa. (d) Conventional cell of the Cmcm phase with the eigenvector of the unstable TA(Y) mode indicated by arrows. The arrows show the directions of atomic displacements. Phonon dispersive curves of new predicted P2₁/m (e) phase for CdS at 100 GPa and Pnma (f) phase for CdSe at 80 GPa.

Before starting further discussion on the energetic properties of CdS between new predicted P4/nmm (Z = 2) and P4/nmm (Z = 4), we will make a full analysis on their structural features. It seems that the coordination environment and bonding of Cd atoms and S atoms in P4/nmm (Z = 2) phase are relatively simpler than those in P4/nmm (Z = 4) structure, where the Cd and S atoms are alternately separated. As can be seen in Fig. 3a, Cd atoms in P4/nmm (Z = 2) phase lie at the same planar, and the distance between the nearest neighbour Cd atoms is 2.987 Å. The nearest distance between Cd and S is 2.508 Å. This structure consists of interleaving stacked hexahedron composed of Cd atoms, while the S atom locates at the centre of hexahedron. Although the two nearest Cd–S atoms become closer in P4/nmm (Z = 2), there is still no covalent bonding through our electron localization function analysis (Fig. S2†). While, P4/nmm (Z = 4) structure is composed of non-equilateral dual dodecahedron which are perpendicular to each other in Fig. 3b; the shortest Cd–S bond length is 2.597 Å, which is slightly longer than that of P4/nmm (Z = 2). The shortest Cd–Cd bond length is 2.632 Å and the shortest S–S bond length is 2.709 Å. It is found that the volume of the P4/nmm (Z = 2) phase is much smaller than that of P4/nmm (Z = 4) structure between 100 and 140 GPa. Thus, the denser packing makes the P4/nmm (Z = 2) structure energetically favorable. Its optimized lattice parameters of the P4/nmm (Z = 2) structure are a = b = 4.07 Å, c = 3.03 Å at 100 GPa. The atomic coordinates were as follows: S (0, 0, 0.918) and Cd (0, 0, 0.5). Intriguingly, this P4/nmm structure (Z = 2) has been found as a high-pressure phase in ZnO sitting in between NaCl and CsCl phase distortion.³⁴ However, P4/nmm (Z = 4) structure becomes more stable above 150 GPa.

Fig. 3 Crystal structures of CdS with the tetragonal symmetry P4/nmm (Z = 2) (a) and (Z = 4) (b).

For the CdSe, we found a new orthorhombic phase (Pnma) between Cmcm and P4/nmm phases, which is obviously different from that of ZnS (Cmcm → P4/nmm). Moreover, the P2₁/m structure in CdS becomes energetically much less favorable in CdSe and CdTe, as can be seen from Fig. 1. This indicates that the structures and phase transition sequences strongly correlate with the chalcogens. To further understand the phase mechanism of CdSe, we give phonon dispersive curves of Cmcm phase at 50 GPa (Fig. 2c), and it is found that TA phonon modes become severely softened at the zone boundary Y point with imaginary phonon frequencies. In CdSe system, the structural phase transition mechanism of Cmcm → Pnma has been revealed by the analysis of TA(Y) phonon softening in Cmcm phase (Fig. 2d), and an orthorhombic path with Pnma symmetry is accordingly proposed. It is found that the lowest-energy structure is formed when the distortion along the [100] direction (Fig. S3†). Fig. 1b gives the thermodynamically stable region of the Pnma phase for CdSe is from 44 GPa to 72 GPa. Its optimized lattice parameters are a = 5.00 Å, b = 4.82 Å, c = 5.17 Å at 60 GPa. The atomic coordinates were list as follows: Se (0.322, 0.75, 0.927) and Cd (−0.163, 0.75, 0.084). Meanwhile, the lattice dynamics calculations with no imaginary phonon frequencies support the dynamics stability of new unravelled Pnma phase for CdSe up to 80 GPa (shown in Fig. 2f). P4/nmm phase (Z = 2) shown in CdS has also been found in CdSe and becomes more stable in energy than any other structures between 72 GPa and 90 GPa. Moreover, we have included the earlier proposed CsCl phase in the enthalpy calculation (Fig. 1). Yet its apparent high energy compared to those of the predicted monoclinic P2₁/m phase, an orthorhombic Pnma and P4/nmm phase (Z = 2) enable us to fairly exclude its occurrences in CdS and CdSe.

Based above analysis, the pressure-induced dissociation in CdX was observed (Fig. 1), yet it is quite unexpected. After examining the structural characters under strong compression, we obtained a sandwich-like structure made up of alternate Cd and X (X = S, Se and Te) atomic blocks (Fig. 4). This peculiar sandwich arrangement is mainly favor of the interactions of the same kind of atoms. The direct Cd–X bonding is significantly frustrated. This suggests a tendency toward decomposition into Cd + X at such high pressures. To give some hints for experimental study, we calculated the decomposition enthalpies by adopting hcp structure for Cd, S-III structure for S, Se–V (β-Po) structure for Se, and Te–V (bcc) structure for Te, respectively. The decomposition pressures have been found for CdS (129 GPa), CdSe (90 GPa) and CdTe (34 GPa), respectively, which greatly decreases with increasing the atomic radius of the chalcogens.

Fig. 4 (a) Predicted P3̄m1 crystal structure of CdTe at 60 GPa. (b) Predicted C2/m structure of HgS at 80 GPa. (c) Phonon dispersion curves of P3̄m1 structure for CdTe at 55 GPa. (d) Phonon dispersion curves of C2/m phase for HgS at 100 GPa.

One question is naturally raised about the low dissociation pressure (34 GPa) in CdTe, which contradicts the experimentally reported stability of Cmcm phase up to around 42 GPa. About this phenomenon, there are two possible reasons that need to be pointed. Firstly, we do not consider the temperature effect in our calculations, but experience tells us that room temperature is not very high to significantly modify the dissociation pressure. Secondly, we propose that there exists a large kinetic energy barrier for dissociation, and extra pressure is added to overcome this energy barrier. This resembles the high pressure synthesis of transition metal nitrides^38–42 and zinc chalcogenides^20,33 from the elemental constituents, in which much higher pressures are necessary to promote the reaction. Similar phenomenon has been found in ZnTe.²⁰ A lesson learned from the knowledge on CdTe suggests that the experimental observation of the dissociation pressures in CdS and CdSe could be higher than the results predicted by the static enthalpy calculation (Fig. 1). In addition, we also focus on the experimentally observed unsolved phase above 42 GPa in CdTe,²² although it is metastable versus the dissociation. Through our CALYPSO simulations, we found a hexagonal P3̄m1 structure, as can be seen in Fig. 4a, which is lower in energy than Cmcm phase above 44 GPa. Meanwhile, the lattice dynamics calculations with no imaginary phonon frequencies support the dynamics stability of hexagonal P3̄m1 phase over the pressure range studied here (Fig. 4c). However, the simulated XRD spectra of the P3̄m1 phase are obviously deviated from the experimental one (Fig. S4†). The search for this structure might not be finished.

3.2 Mercury chalcogenides

The amazing similarity between HgX (X = S, Se and Te) and CdX has been observed. At high pressure, sandwich-like structures made up of alternate Hg and X (X = S, Se and Te) atomic blocks were also obtained, which indicated a strong decomposition tendency into Hg + X (X = S, Se and Te). However, before the dissociation of HgX, we have successfully reproduced low-pressure phase transition sequence, namely, cinnabar phase or zinc blende structure → rocksalt structure (→Cmcm phase). We have also investigated the decomposition enthalpies by adopting Hg–I structure for Hg, S-III structure for S, Se–I structure for Se, and Te–I structure for Te, respectively. It is worth noting that the dissociation becomes more favourable to the given phase in HgX (X = S, Se and Te). Meanwhile, we also committed to find that the experimentally observed unsolved phase at 52 GPa in HgS. A metastable phase (space group: C2/m, Z = 4) for HgS is presented at P = 57 GPa higher than decomposition of pressure (Fig. 5a). Our phonon calculation (Fig. 4d) has confirmed that this C2/m phase is dynamically stable with the absence of the imaginary phonon frequency up to 100 GPa. Its optimized lattice parameters are a = 4.29 Å, b = 3.66 Å, c = 13.73 Å, and β = 102.2° at 80 GPa (Fig. 4b). The atomic coordinates after the geometry optimization were as follows: S1 (0.327, 0, 0.049), S2 (0.981, 0, 0.146), Hg1 (0.607, 0, 0.278), and Hg2 (0.204, 0, 0.427). Unfortunately, there is very limited diffraction information.¹⁶ So, we can not determine that whether the predicted C2/m is the experimental HgS-III. Further experimental information is highly demanded.

Fig. 5 Calculated enthalpy curves versus pressure for the various HgX structures and decomposition into Hg + X relative to the NaCl phase for HgS or Cmcm phase for HgSe and HgTe, respectively.

The pressure-induced dissociations for cadmium and mercury chalcogenides were strongly confirmed by our enthalpy calculations (Fig. 1 and 5). The physical mechanism for this dissociation is rather complex and challenging. Here, we try to provide the possible argument. At ambient and lower pressure, cadmium and mercury chalcogenides are fourfold coordinated. Their s-p valence electrons are hybridized and form s¹ + p³ = sp³ directed covalent valence. Because of electronegativity difference between the atoms, there is certain ionic bonding. Under strong compression, the above structures vary in coordination number from 4 to 8. At the same time, the inter-atomic distances become much shorter and electron bands are largely widened. Thus, the covalent bonds are destroyed and ionic interactions are greatly weakened due to the highly delocalized valence electrons. When pressure is high enough, the dislocation into elemental substances occurs. Notably, much theoretical effort is highly demanded to understand this phenomenon.

4. Conclusions

We have extensively investigated the structural phase transitions of the cadmium and mercury chalcogenides (CdX and HgX, X = S, Se and Te) under pressure using the swarm-intelligence based CALYPSO method. The phase transitions sequence for cadmium chalcogenides (CdX, X = S and Se) was wurtzite structure or zinc blende structure → rocksalt structure → Cmcm (Pmmn, P2₁/m or Pnma) phase → P4/nmm phase (Z = 2) → Cd + X. However, the structural phase transition sequence of mercury chalcogenides (HgX, X = S, Se and Te) is cinnabar phase or zinc blende structure → rocksalt structure → Cmcm phase → Hg + X. It is interesting to note that we have discovered an intriguing phenomenon of pressure-induced dissociation into Cd (Hg) + X. We proposed that a large kinetic barrier might be responsible for the predicted low dissociation pressure in CdTe and HgS. The uncovered pressure-induced decomposition of IIB-VIA compounds has important implications for the other binary compounds.

Acknowledgements

We are thankful for the National Natural Science Foundation of China under Grant No. 21573037 and No. 11404035, the Science Foundation of Jilin Province under Grant No. 20150101004JC and 20150101042JC, the Science Foundation for Youths of Jilin Province under Grant No. 20130522146JH and Industrial Technology Research Project (2014Y135).

Notes and references

1. E. Cartlidge, Nature, 2014 DOI:10.1038/nature.2014.16552.
2. M. S. Miao, Nat. Chem., 2013, 5, 846.
3. L. Zhu, H. Y. Liu, C. J. Pickard, G. T. Zou and Y. M. Ma, Nat. Chem., 2014, 6, 644.
4. W. Zhang, A. Oganov, A. Goncharov, Q. Zhu, S. Boulfelfel, A. Yakhov, E. Stavrou, M. Somayazulu, V. Prakapenka and Z. Konopkova, Science, 2013, 342, 1502.
5. J. Botana and M. S. Miao, Nat. Commun., 2014, 5, 4861.
6. Y. W. Li, Y. C. Wang, C. J. Pickard, R. J. Needs, Y. Wang and Y. M. Ma, Phys. Rev. Lett., 2015, 114, 125501.
7. I. Errea, M. Calandra, C. J. Pickard, J. Nelson, R. J. Needs, Y. W. Li, H. Y. Liu, Y. W. Zhang, Y. M. Ma and F. Mauri, Phys. Rev. Lett., 2015, 114, 157004.
8. C. E. Hurwitz, Appl. Phys. Lett., 1996, 8, 121.
9. F. H. Nicoll, Appl. Phys. Lett., 1996, 9, 13.
10. H. S. Güder, S. Gilliland, J. A. Sans, A. Segura, J. González, I. Mora, V. Muñoz and A. Muñoz, Phys. Status Solidi B, 2003, 235, 509–513.
11. V. V. Shchennikov and S. V. Ovsyannikov, Phys. Status Solidi B, 2007, 244, 437–442.
12. J. C. Phillips, Bonds and Bands in Semiconductors, Academic, New York, 1973.
13. W. A. Harrison, Electronic Structure and the properties of Solids, Freeman, San Francisco, 1980.
14. S. Wei and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6944.
15. A. Mujica, A. Rubio, A. Munoz and R. J. Needs, Rev. Mod. Phys., 2003, 75, 863.
16. T. Suski and W. Paul, High Pressure in Semiconductor Physics I (Semiconductors & Semimetals), Academic Press, 1998, vol. 54.
17. D. Errandonea, A. Segura, D. Martínez-García and V. Muñoz-San Jose, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125203.
18. S. Adachi, Properties of Group-IV, III-V and II-VI Semiconductors, John Wiley & Sons, Ltd., 2005.
19. A. N. Chantis, M. V. Schilfgaarde and T. Kutani, Phys. Rev. Lett., 2006, 96, 086405.
20. K.-U. Gawlik, L. Kipp and M. Skibowski, Phys. Rev. Lett., 1997, 78, 16.
21. Z. W. Li, H. B. Wang, Y. Li, Y. M. Ma, T. Cui and G. T. Zou, New J. Phys., 2010, 12, 043058.
22. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
23. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063 . The CALYPSO code is free for academic use; please register at http://www.calypso.cn.
24. J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, Phys. Rev. Lett., 2011, 106, 015503.
25. L. Zhu, H. Wang, Y. C. Wang, J. Lv, Y. M. Ma, Q. L. Cui, Y. M. Ma and G. T. Zou, Phys. Rev. Lett., 2011, 106, 145501.
26. G. C. Yang, Y. C. Wang and Y. M. Ma, J. Phys. Chem. Lett., 2014, 5, 2516.
27. M. Zhang, H. Y. Liu, Q. Li, B. Gao, Y. C. Wang, H. D. Li, C. F. Chen and Y. M. Ma, Phys. Rev. Lett., 2015, 114, 015502.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
29. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
30. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
31. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
32. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184101.
33. V. Ozolinš and A. Zunger, Phys. Rev. Lett., 1999, 82, 767.
34. Z. W. Li, Y. Xu, G. Y. Gao, T. Cui and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 193201.
35. S. B. Zhang and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 1450.
36. A. Mujica and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 9659.
37. Y. Li, L. J. Zhang, T. Cui, Y. M. Ma, G. T. Zou and D. D. Klug, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 054102.
38. J. Y. Zhang, L. J. Zhang, T. Cui, Y. Li, Z. He, Y. M. Ma and G. T. Zou, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104115.
39. J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275.
40. Y. Li, H. Wang, Q. Li, Y. M. Ma, T. Cui and G. T. Zou, Inorg. Chem., 2009, 48, 9904.
41. A. F. Young, C. Sanloup, E. Gregoryanz, S. Scandolo, R. J. Hemley and H. Mao, Phys. Rev. Lett., 2006, 96, 155501.
42. D. Åberg, B. Sadigh, J. Crowhurst and A. F. Goncharov, Phys. Rev. Lett., 2008, 100, 095501.

---

Footnote

† Electronic supplementary information (ESI) available: The energy evolution related to phase transitions of NaCl → P2₁/m CdS with the relevant atom displacement. The calculated electron localization functions (ELF) of tetragonal P4/nmm (Z = 2) phase for CdS at 120 GPa. The simulated X-ray diffraction patterns for the metastable P3̄m1 phase of CdTe are compared with the experimental data for the unresolved phase at 42 GPa. See DOI: 10.1039/c5ra21673g

---