Random site occupancy induced disordered Néel-type collinear spin alignment in heterovalent Zn²⁺–Ti⁴⁺ ion substituted CoFe₂O₄

Abstract

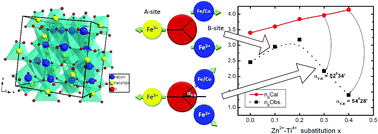
CoFe₂O₄, cobalt ferrite (CFO) nano-particles with composition CoZn_xTi_xFe_2−2xO₄ (0 ≤ x ≤ 0.4) were synthesized by sol–gel autocombustion method. The effect of Zn²⁺–Ti⁴⁺ substitution on the structural, magnetic and frequency dependent permeability properties of the CFO nano-particles were investigated by X-ray diffraction, ⁵⁷Fe Mössbauer spectroscopy, vibrating sample magnetometry, transmission electron microscopy and permeability analysis. The Rietveld refinement of XRD patterns confirm the single spinel phase and the crystallite size is found in the range of 22–32 nm. Cation distribution was estimated by refining the XRD pattern by Rietveld method, and shows Zn²⁺ ions at the tetrahedral A-sites, and Co²⁺ and Ti⁴⁺ ions at octahedral B-sites. The saturation magnetization (M_s) increased from 58 to 75 emu g⁻¹ for up to x = 0.2 and then decreased, while the coercivity decreased continuously with Zn²⁺–Ti⁴⁺ substitution. Two distinct composition ranges with Zn²⁺–Ti⁴⁺ substitution are identified for which M_s variation with x is explained by the Néel and Yafet–Kittel models. The room temperature Mössbauer spectra are analyzed in detail for probing the magnetic properties of Fe based Zn²⁺–Ti⁴⁺ substituted CFO. The effect of Zn²⁺–Ti⁴⁺ substitution on various Mössbauer parameters, viz. hyperfine field distribution, isomer shift, quadrupole splitting, and line width, has also been studied. The variation of nuclear magnetic fields at the A and B sites is explained on the basis of A–B and B–B supertransferred hyperfine interactions. The CFO nanoparticle is considered to possess a fully inverse spinel structure with a Néel-type collinear spin alignment, whereas the Zn²⁺–Ti⁴⁺ substitution in CFO is found to be structurally and magnetically disordered due to the nearly random distribution of cations and the canted spin arrangement. This study also demonstrates that one can tailor the magnetic properties of CFO particles by optimizing the Zn²⁺–Ti⁴⁺ substitution. The increase in the permeability, saturation magnetization and lower loss factor makes the synthesized materials suitable for applications in microwave devices and deflection yokes.

---

1. Introduction

The spinel ferrite crystal structure has the space group Fd3m (F⁴_1/d3̄_2/m, no. 227 in the International Tables) which consists of 56 atoms; 32 are oxygen anions assuming a close packed cubic structure, and the remaining are metal cations residing on 8 of the 64 available tetrahedral (A) sites and 16 of the 32 available octahedral (B) sites. The size and valence state of the cation species determine the filling of these sites and strongly influence the material's magnetic and electrical properties.

Cobalt ferrite (CFO) crystallizes in an inverse spinel structure. The inverse spinel form of CFO is represented generally as A^3+(TET)[B²⁺, B³⁺]^(OCT)O₄ where the tetrahedral A-sites are occupied by Fe³⁺ cations and octahedral B-sites are occupied by Fe³⁺ ions and the divalent Co²⁺ ions respectively.¹ In CFO, the magnetic interactions between these metal ions, limited only to the nearest neighbors, are antiferromagnetic in nature and their magnitudes are given by exchange integrals. For example, the exchange integral J_AB describes the nature and strength of the interaction between any two nearest A and B ions. Similarly, J_AA, J_BB and J_AB are the exchange integrals showing the strength of any A–A, B–B and A–B nearest neighbor interactions respectively. Generally, when the A and B sub-lattices are occupied by the magnetic ions of the same type, the relative strengths are given by |J_AB| ≫ |J_BB| > |J_AA|: thus, the moments on A- and B-sites are aligned anti-parallel to each other and this impels the two A–A and B–B moments to be parallel despite the antiferromagnetic exchange interactions between them, so these moments are in frustrated state. One can in principle alter the relative strengths of all these exchange integrals by changing the type of the magnetic ions on A and B sites.² CFO is widely used as a material for high-density data recording and storage systems,³ biomedical hyperthermia inductors etc.^4,5 The requirements for the values of coercivity (Hc) depend on the application of CFO. Characteristic values of coercivity for permanent magnets are 480–640 kA m⁻¹ and more, for magnetic recording 200–280 kA m⁻¹ and for biomedical applications as low as possible.⁶ CFOs are being used for magnetic recording applications due to good intrinsic properties. These intrinsic magnetic properties, i.e. saturation magnetization (M_s) and coercivity (Hc) can be modified by the cationic substitution of Fe³⁺ ions. However, the substitution causes intrinsic Hc to decrease effectively at the expense of decrease in M_s, restricting their use for recording applications. Thus increasing efforts are being made to decrease coercive force and simultaneously increasing M_s with substitution. The value of the M_s must be high independent of application. Therefore, the preparation of CFO with high M_s and controlled Hc is a problem of today. In recent years, this problem is solved by heterovalent substitution of Fe³⁺ according to the scheme 2Fe³⁺ − Me²⁺ + Me⁴⁺, where Me²⁺ and Me⁴⁺ are ferromagnetic and nonmagnetic ions respectively. Such substitution ensures electrical neutrality in the CFO structure. Tailored coercivity materials, which might be of use in recording media such as hard discs, floppy discs and videotapes, can be prepared by the substitution of Co²⁺–Ti⁴⁺,⁷ Zn²⁺–Ti⁴⁺,⁸ Co²⁺–Sn⁴⁺,⁹ Mn²⁺–Si⁴⁺,¹⁰ Co²⁺–Mo⁴⁺,¹¹etc. ions into the ferrite.

Doping with aliovalent ions (Ti⁴⁺) is used to break the coupling of ferrimagnetically active oxygen polyhedral in spinel ferrite. Ti⁴⁺ is believed that, are dissolved in the spinel matrix of the material and through this they directly affect the magnetic properties of the crystal structure. Zinc ferrite, ZnFe₂O₄, is a normal spinel, and such the unit cell has no net magnetic moment (ZnFe₂O₄/Zn²⁺[Fe³⁺Fe³⁺]O₄/d⁰[d⁵d⁵]). CFO is an inverse spinel and, consequently, the two magnetic sublattices are antiferromagnetically aligned (CoFe₂O₄/Fe³⁺[Co²⁺Fe³⁺]O₄/d⁵[d⁵d⁵]). When the nonmagnetic Zn²⁺(d¹⁰) is substituted into the CFO crystal lattice, it has a stronger preference for the tetrahedral site than does the ferric ion and thus reduces the amount of Fe³⁺ on the A site. Because of the antiferromagnetic coupling, the net result is an increase in magnetic moment on the B lattice and an increase in saturation magnetization (Zn_x²⁺Fe_1−x³⁺[Co²⁺Fe³⁺]O₄/d_x¹⁰d_1−x⁵[d⁵d⁵]). Therefore, in particular, it has been shown that Zn²⁺–Ti⁴⁺ cationic mixtures produce materials with suitable characteristics for high-density magnetic recording. Also, it has been reported that site preference of Zn²⁺ ions can provoke an increase in the saturation magnetization, M_s, and reduce the switching field distribution (SFD) of the particles, which is an important parameter in magnetic recording applications.¹² On the other hand, the replacement of iron ions by Ti⁴⁺ on A-site can also increase M_s.¹³ Ti⁴⁺ ion substitution at iron site in ferrites is known to be effective in reducing magnetocrystalline anisotropy and enhancing the electrical resistivity, these properties are suitable for wide range of industrial applications.¹⁴

Mössbauer spectroscopy is an effective method for investigating the local environment of nuclei, and namely the nature of the cationic site distribution. The presence of non-magnetic ions in spinel ferrites is found to alter their magnetic and electric properties. Such isomorphous substitutions in iron oxides are particularly apparent in their Mössbauer spectra, since these will drastically reduce magnetic interactions, resulting in lower magnetic ordering temperature and decreased magnetic field supertransfer (i.e., lower hyperfine fields).

In an attempt to shed more light on the origin of the magnetic changes when the substitutions are made, and in order to improve the M_s and Hc of CFO for specific application; the family of compounds, CoZn_xTi_xFe_2−2xO₄, where x ranges from 0.0 to 0.4, has been prepared and investigated using X-ray diffraction, vibrating sample magnetometer, permeability and Mössbauer spectroscopy.

2. Material synthesis and characterization

A series of spinel ferrite with formula CoZn_xTi_xFe_2−2xO₄ (0 ≤ x ≤ 0.4) was prepared by sol–gel auto combination method. All AR grade metal nitrates of Co, Zn, Ti and Fe were used for the synthesization of desired material. Citric acid (C₆H₈O₇) as a fuel was added into aqueous solution of metal nitrate. The metal nitrate to citric acid (C₆H₈O₇) ratio was kept as 1 : 3 and then the pH of the mixed solution was kept at 7 by adding ammonia solution. The mixed solution was evaporated to dryness by heating at 80 °C on a hot plate with continuous stirring and finally formed a very viscous brown gel. This viscous brown gel was ignited by increasing the temperature up to 100 °C and the loose powder of the samples was obtained. Finally, the as burnt powder was annealed at 600 °C for 4 h to obtain Zn²⁺–Ti⁴⁺ substituted CFO ferrite nanoparticles. Chemical reaction of formula CoZn_xTi_xFe_2−2xO₄ is shown in Fig. 1.

Fig. 1 Chemical reaction of CoZn_xTi_xFe_2−2xO₄ synthesized by sol–gel autocombustion method.

The phase formation identification of samples prepared was characterized by X-ray diffraction (XRD, Philips X'Pert instrument) with Cu Kα radiation (wave length λ = 1.54056 Å) at room temperature. Transmission electron microscope (TEM) measurements were recorded on Philips (Model CM 200). Magnetic measurements were performed at room temperature using a commercial PARC EG&G vibrating sample magnetometer VSM 4500. Magnetic hysteresis loops were measured at room temperature with maximum applied magnetic fields up to 1 T.

The initial permeability (μ_i) measurements on the toroid-shaped samples were conducted as a function of frequency. The initial permeability measurements of the toroid samples were taken using a HP-4284A LCR precision meter. Mössbauer spectra of all the samples were recorded at room temperature using a Mössbauer spectrometer (Nucleonix Systems Pvt. Ltd., Hyderabad, India) operated at a constant acceleration mode (triangular wave) in transmission geometry at room temperature. The source employed was Co⁵⁷ in Rh matrix of strength 50 mCi. The calibration of the velocity scale is done by using an enriched α-⁵⁷Fe metal foil. The line width (inner) of calibration spectrum is 0.23 mm s⁻¹.

3. Results and discussion

3.1 Structural properties

Fig. 2 demonstrates the Rietveld refined X-ray diffraction pattern of all the samples of CoZn_xTi_xFe_2−2xO₄ ferrite system. The pattern shows the formation of single phase cubic spinel structure with a space group Fd3m and without any signature of secondary phase. The data were processed to realize the conditions of the software program FullProf for the structure refinement. Crystal structure of the Zn²⁺–Ti⁴⁺ substituted CFO were generated from the Rietveld refinement and same is presented in Fig. 3. All the results obtained from the refinement of the structure are correlated with Zn²⁺–Ti⁴⁺ substitution. The values of discrepancy factor (R_wp) and expected (R_exp) values with goodness of fit (χ²) index are given in Table 1. The XRD pattern shows the presence of (220), (311), (222), (400), (422) and (511). The analysis of XRD pattern reveals the formation of single phase cubic spinel ferrite and no extra peak other than cubic spinel phase is detected. The XRD pattern also shows slight shift in peak position toward lower 2θ angle due to the substitution of Zn²⁺ and Ti⁴⁺ ions. The lattice parameter was also calculated from the following relation:¹⁵

Fig. 2 Rietveld refined X-ray diffraction patterns of CoZn_xTi_xFe_2−2xO₄.

Fig. 3 Cubic spinel crystal structure of CoZn_xTi_xFe_2−2xO₄ (x = 0.2).

Table 1 Discrepancy factor (R_wp), expected values (R_exp), goodness fit factor (χ²), lattice constant (a_xrd and a_Riet), crystallite size (t_xrd) and particle size (t_TEM) of CoZn_xTi_xFe_2−2xO₄

x	R exp	R wp	χ ^2	‘axrd’	‘aRiet’	t xrd	t TEM
0.0	4.5	3.5	1.65	8.3864	8.3668	22	24
0.1	3.6	3.6	1.00	8.3949	8.3989	24	28
0.2	8.2	8.1	1.02	8.4019	8.4019	28	27
0.3	9.5	8.4	1.28	8.4068	8.4093	28	31
0.4	6.5	5.2	1.56	8.4122	8.4132	32	35

---

Table 1 shows the variation of lattice parameter with Zn²⁺–Ti⁴⁺ substitution calculated by using eqn (1) (a_xrd) and Rietveld method (a_Riet). Lattice constant of each sample were also calculated using the extrapolation function F(θ) i.e. the Nelson–Riley function for each reflection of the studied sample was calculated:¹⁶

The values of the lattice constant ‘a’ are drawn in the Fig. 4 as a function of F(θ) for all x values. The relation in Fig. 4 represents straight line for each value of x. The true values of the lattice parameter ‘a₀’ can easily be obtained by extrapolating the line to the value F(θ) = 0 or θ = 90°. It is observed that lattice constant of CFO increased with increase in Zn²⁺–Ti⁴⁺ substitution, this is due to the difference in combined ionic radii of Zn²⁺ (0.82 Å) and Ti⁴⁺ (0.60 Å) that replaces Fe³⁺ (0.67 Å) ions.

Fig. 4 Variation of lattice constant with F(θ) of CoZn_xTi_xFe_2−2xO₄.

Average crystallite diameter ‘D_xrd’ of powder estimated from the most intense (311) peak of XRD and using the Scherrer method:

where B_1/2 is the full width of half maximum in (2θ), θ is the corresponding Bragg angle and C = 0.9. The values of crystallite diameter are presented in the Table 1. It is observed that particle size increased from 22–32 nm with increase in Zn²⁺–Ti⁴⁺ substitution.

In order to study the morphology and phase structure of the synthesized samples, the samples were examined using transmission electron microscopy (TEM). Particle size determined from the TEM is in the range of 24–35 nm (Table 1). Fig. 5 shows TEM images of the typical samples (x = 0.0 and 0.4), that confirmed the particles are aggregated. Most of the nanoparticles appeared spherical in shape with small thickness. TEM image shows that the synthesized ferrite nanoparticles are agglomerated to some extent due to the interaction between magnetic nanoparticles.

Fig. 5 TEM images of typical samples of CoZn_xTi_xFe_2−2xO₄.

Cation distribution. The cation distribution estimation was made from intensity ratio and using FullProf program. The data were processed to analyze using the computer Program FullProf.2 k (Version 4.30-Apr2008-ILL JRC) in the Rietveld method for structure refinement. Program refinement of the first samples was started with the space group Fd3m, origin at 3̄m, O in 32e-, A-site in 8f and B-site in 16c. In the first step the global parameters, such as 2θ-zero and background, were refined. In the next step, the structural parameters such as lattice parameter, atomic coordinates, and site occupancy, were refined. The fitting quality of the experimental data were checked by using the following parameters: the goodness of fit, χ²; that must tend to one and two reliability factors, R_exp and R_wp (weighted differences between measured and calculated values) that must be close to or less than 10%.

Cation distribution of all the samples are obtained from the Rietveld refinement of X-ray diffraction patterns and presented in Table 2. The occupancies of some of the cations were fixed on the basis of their site preferences. It is known that Zn²⁺ ions have marked preference for tetrahedral A-site and similarly Co²⁺ ions have been reported to have strong preference for octahedral B-site due to their d²sp³ hybridization. But Co²⁺ ions were found not to occupy the A-sites and small percentage of Co²⁺ on A-site was deteriorating the agreement factors. Therefore, these cations were made to occupy their most preferential sites throughout the refinement. The Ti⁴⁺ ions are generally known to have octahedral (B) site preference.¹⁷ Initially they were placed on the B-sites in the refinement model. However, the calculated profile could not be matched with the experimental one unless Ti⁴⁺ ions were allowed to occupy the A-sites also with small percentage.

Table 2 Values of atomic coordinates (x, y, z) and occupancy (g) determined from Rietveld refinement of XRD pattern of CoZn_xTi_xFe_2−2xO₄

Atom	x = 0.0		x = 0.1		x = 0.2		x = 0.3		x = 0.4
	x = y = z	Occ. (g)	x = y = z	Occ. (g)	x = y = z	Occ. (g)	x = y = z	Occ. (g)	x = y = z	Occ. (g)
Co	0.1250	0.0998(2)	0.1250	0.1002(2)	0.1250	0.1100(3)	0.1250	0.1405(2)	0.1250	0.1604(3)
Zn	0.1250	0.0000	0.1250	0.0999(1)	0.1250	0.1998(2)	0.1250	0.3000(1)	0.1250	0.3999(1)
Ti	0.1250	0.0000	0.1250	0.0204(1)	0.1250	0.0399(1)	0.1250	0.0400(2)	0.1250	0.0500(1)
Fe	0.1250	0.8998(2)	0.1250	0.7800(1)	0.1250	0.6495(2)	0.1250	0.5192(1)	0.1250	0.3891(2)
Co	0.5000	0.8999(2)	0.5000	0.8999(1)	0.5000	0.8895(2)	0.5000	0.8590(3)	0.5000	0.8393(1)
Ti	0.5000	0.0000	0.5000	0.0796(1)	0.5000	0.1599(1)	0.5000	0.2599(1)	0.5000	0.3499(1)
Fe	0.5000	1.0999(1)	0.5000	1.0200(2)	0.5000	0.9503(2)	0.5000	0.8806(1)	0.5000	0.8106(1)

---

The mean ionic radii of tetrahedral A-site (r_A), octahedral B-site (r_B), theoretical lattice parameter (a_th) and oxygen parameter (u) were calculated using the equations discussed elsewhere.¹⁸ The values of these parameters are listed in Table 3. It is observed that r_A increased whereas r_B decreased with Zn²⁺–Ti⁴⁺ substitution. This behavior is directly related to site occupancy of cation at A and B site. It is observed that the variation of a_th is similar to a_Riet and a_xrd. The oxygen positional parameter ‘u’ is given by the distance between an oxygen ion and a face of a cube. In an ideal FCC structure u = 3/8 = 0.375 Å, where the packing of ions within the lattice is taken as perfect. The increased value in ‘u’ parameter may be associated with the shift of the origin at the tetrahedral sites with the decreasing number of Fe ion at the octahedral sites. That is, the distortion of the lattice, and the deviation from FCC ideal case. Further, the increasing value of u reveals the need for the structure to allow progressive expansion of the tetrahedral A-site so as to accommodate larger Zn²⁺ ions.

Table 3 Mean ionic radii at tetrahedral A-site (r_A), octahedral B-site (r_B), theoretical lattice constant (a_th) and oxygen positional parameter (u) of CoZn_xTi_xFe_2−2xO₄

x	A-site (rA)	B-site (rB)	a th	u
0.0	0.612	0.692	8.342	0.3837
0.1	0.636	0.690	8.371	0.3849
0.2	0.659	0.687	8.399	0.3861
0.3	0.685	0.682	8.428	0.3874
0.4	0.710	0.679	8.457	0.3886

---

3.2 Permeability

Initial permeability (μ_i) investigation on the samples was carried out as a function of composition and frequency. Initial permeability showed dispersion at low frequency and decreases with frequency as shown in Fig. 6. Initial permeability would be due to the contribution from spin rotation and from the domain-wall motion. But the contribution from spin rotation is found to be smaller than domain-wall motion. It is mainly due to reversible motion of domain walls in the presence of weak magnetic field, and the contribution of spin rotation is negligible small.^19,20 The initial permeability contributed by domain-wall motion is expressed as;where M_s is the saturation magnetization, D_m the average grain size and γ_w is the domain-wall energy. At low frequency, changes of the magnetization direction occur by the motion of domain walls, so that a domain oriented in the direction of the applied field grows at the expense of its neighbours which are oriented in different direction. At higher frequency the domain wall is unable to move sufficiently rapidly to follow the alternating field. The overall magnetization vector does not follow the applied field hence accounting for the low value of permeability. The initial permeability in ferrites is known to be interplay of various factors like grain size (D_m), density, porosity, saturation magnetization (M_s), anisotropy (K₁), etc.:where μ_i is the initial permeability, σ is stress, β is the volume concentration of impurity and δ is the thickness of domain wall. The permeability mechanism may be explained in terms of domain wall displacement and rotation of spins in each domain. It is observed that as the concentration of Zn²⁺–Ti⁴⁺ is increased the grain size increases. According to Globus¹⁹ a linear relationship exists between the grain diameter and permeability. The diameter of a Bloch wall is related to the grain size as the wall is taken to be fixed to the grain boundary along its circumference. As the size of the grains becomes larger, the domains and their wall motion would increase; causing the permeability to increase. The substitution of Zn²⁺–Ti⁴⁺ is in CFO ferrite also increase particle size as discussed earlier which eventually enhance the densification and reduces the internal stress leading to decreasing magneto-crystalline anisotropy. This leads to a decrease in the hindrance given to the movement of domain walls resulting in increased value of μ_i.²¹ The variation of magnetic loss factor (tan δ/μ_i) with frequency is shown Fig. 7. The rapid increase in the loss factor at frequencies above 5 MHz may be attributed to the phenomenon of domain wall relaxation, which involves the hindrance of domain wall motions of small grains, by those of larger grains where the population of larger grains is smaller. The major contribution to the magnetic losses in ferrites is due to hysteresis losses, which in turn is based on damping phenomena associated with irreversible wall displacement and spin rotations. However, the hysteresis loss becomes less important in the high-frequency range because the wall displacement is mainly damped and the hysteresis loss will be due to spin rotation.²² It is observed that the values of loss factor decreased for x ≤ 0.2 with the increase in Zn²⁺–Ti⁴⁺ substitution. The values of loss factor are also known to depend on various factors such as stoichiometry, Fe²⁺ content, and structural homogeneity, which in turn depend on the composition, and sintering temperature of the samples.²³ Because of low-melting point of Ti⁴⁺, insulating phases may form at the grain boundaries, which could increase the electrical resistivity of the material. This has as a consequence of the reduction of the ohmic currents developed through the body of the material during operation under alternating currents and finally a reduction of the total power losses.²⁴ It is inferred from the present study that Zn²⁺–Ti⁴⁺ ions have remarkably enhanced initial permeability of CFO and consequently the lower magnetic loss factor was observed. The magnetic loss factor values are found to be small even at higher frequencies for these samples, which is one of the criteria for the materials to be used in microwave devices and for deflection yoke.

Fig. 6 Variation of initial permeability with logarithm of frequency.

Fig. 7 Variation of loss factor with logarithm of frequency.

3.3 Magnetization

Fig. 8 shows hysteresis loops of Zn²⁺–Ti⁴⁺ substituted CFO samples. It is observed from Fig. 8 and 9 that saturation magnetization (M_s) increased up to x = 0.2 and thereafter it decreases with increase in Zn²⁺–Ti⁴⁺ substitution. The magnetic properties of Zn²⁺–Ti⁴⁺ substituted CFO is depended on the site distribution of Zn²⁺–Ti⁴⁺ ions and the strength of the exchange interaction among magnetic ions. The behavior in magnetization is related to following factors;

Fig. 8 Variation of magnetization with applied magnetic field.

Fig. 9 Variation of saturation magnetization (M_s) and coercivity (Hc) with Zn²⁺–Ti⁴⁺ substitution.

(i) At x = 0.0, i.e. CoFe₂O₄, material posses inverse spinel structure with a Néel-type collinear spin alignment, where most of the Co²⁺ ions occupy octahedral B-site. When Zn²⁺–Ti⁴⁺ ions are introduced at the cost of Fe³⁺ ions, most of the Zn²⁺ ions and some of Ti⁴⁺ ions occupy A-sites in view of the site preferences for different ions as can be seen from cation distribution (Table 2). This increases the Fe³⁺ ion percentage at B-sites as compared to A-site. As a result, the magnetic moment of B sublattices increases at lower Zn²⁺–Ti⁴⁺ substitution. According to Néel's two sublattice model of ferrimagnetism, the magnetic moments of ions on the A and B sublattices are aligned antiparallel to each other and in a collinear structure (Fig. 10a). However, as Zn²⁺–Ti⁴⁺ substitution increases, A–B super exchange interactions become weak and B–B interactions start to dominate. Instead of collinear antiparallel alignment, a canted structure appears where the spins in B-sites are no longer parallel. The canted (non-collinear) spins naturally lead to a decrease in the value of the B-sublattice magnetization and thus the net magnetization falls off for x > 0.2. The mechanism is presented schematically in Fig. 10.

Fig. 10 Schematic representation of spin arrangements in CoZn_xTi_xFe_2−2xO₄ (a) for x ≤ 0.2; (b) triangular (or Yafet–Kittel) for x ≥ 0.3.

(ii) The magnetic moment of Zn²⁺ and Ti⁴⁺ is zero and for Fe³⁺ is 5 μ_B, the exchange interaction between Zn²⁺–Ti⁴⁺ and Fe³⁺ ions being small, there will be canting of spins of Fe³⁺ and Zn²⁺ ions at the A site. The increase in the Zn²⁺–Ti⁴⁺ content in the sample therefore decreases the magnetic moment of the A sublattice.

(iii) It is expected that in the samples sintered at 600 °C, some of the elements may evaporate. The melting point and the vapor pressure of Zn²⁺ and Ti⁴⁺ being the lowest, much lower than those for other elements, the probability of Zn²⁺ evaporation is maximum. There is a possibility of Fe₂O₃ formation as a result of zinc loss and this can alter the magnetic properties significantly. Any Zn²⁺ loss results in unsaturated oxygen bonds which tend to saturate by bonding with the surrounding B site Fe³⁺ ions reducing them to Fe²⁺. This reduces the Fe³⁺ ion concentration at the B site. The B–B interaction thus becomes relatively weaker, resulting in an increase in magnetization of the B sublattice for lower Zn²⁺–Ti⁴⁺ substitutions. However, for higher Zn²⁺–Ti⁴⁺ substitutions, there being more percentage of Fe³⁺ ions at the B site as compared to A-site, as indicated in point ‘i’ above, the increased B–B interaction reduces the magnetization of the B sublattice.

Here, processes 1 and 3 result in initial increase followed by a decrease in magnetization with increase in Zn²⁺–Ti⁴⁺ substitution, process 2 increases the magnetization with increasing Zn²⁺–Ti⁴⁺ substitution. The observed variation of magnetization in the present work is a sum total of these effects. The net magnetic moment (n_BCal.) is given by the sum of the magnetic moments of A and B sublattices, i.e., M_s = M_B − M_A. For Zn²⁺–Ti⁴⁺ substituted CFO, most of the Zn²⁺–Ti⁴⁺ ions replaces Fe³⁺ ions at A site, leading to a increase in the B-site sublattice magnetization. We use the known magnetic moments for Co²⁺ (3 μ_B), Zn²⁺ (0 μ_B), Ti²⁺ (0 μ_B) and Fe³⁺ (5 μ_B). In this study, the cationic distribution, Zn²⁺ and Ti⁴⁺ ions are non-magnetic and do not contribute to the sublattice magnetization.

The observed magnetic moment (n_BObs.) per formula unit in Bohr magneton (μ_B) was calculated by using the relation:

where M_W is the molecular weight of the sample, n_B is the magnetic moment of the samples expressed in Bohr magneton, M_s is the saturation magnetization. The variation in observed and calculated magnetic moment is shown in Fig. 11. The increasing nature of magneton number can be explained on the basis of Néel two sub-lattice model.²⁵ The decreasing trend for x > 0.2 is due to the nonzero Yafet–Kittel (Y–K) angles in the samples that cannot be explained on the basis of the Néel's two sub-lattice model. This suggests that there are triangular type spin arrangements on B sites (Fig. 10b) which weaken A–B interaction. Further increase in Zn²⁺–Ti⁴⁺ substitution decreases the strength of the exchange interactions, and leads to the lower value of the saturation magnetization and observed magnetic moment.

Fig. 11 Variation of observed (n_BObs.) and calculated (n_BCal.) magneton number with Zn²⁺–Ti⁴⁺ substitution.

The existence of canted spins and reduced magnetic moment with Zn²⁺–Ti⁴⁺ substitution can be observed by determining the Yafet–Kittel angle:²⁶

n_B = (6 + x)cos α_Y–K − 5(1 − x) (7)

where x represents Zn²⁺–Ti⁴⁺ substitution. It increases exponentially with the increase in Zn²⁺–Ti⁴⁺ substitution for x > 0.2 as observed in the inset of Fig. 11. Furthermore, one reasonably believes that the increase in the Y–K angle of magnetic ions means that a decrease in the overlap of the wave functions between two nearest-neighbouring magnetic ions as well as that between magnetic ions and oxygen anions, leads to a reduction in superexchange interactions occurring between the magnetic ions and mediated by the intervening oxygen anions.²⁷ This shows that in the present system of ferrites, randomness increases as Zn²⁺–Ti⁴⁺ is substituted in CFO and shows a significant departure from Néel collinear model.

Coercivity. It is observed from Fig. 8 and 9 that coercivity decreased from 852 to 112 Oe. This can be related to increase in particle size with Zn²⁺–Ti⁴⁺ substitution. As the particle size below a critical size or magnetic exchange length, L_ex, Hc follows a D⁶ power law:²⁸where A is the exchange stiffness constant, and P_c is a constant of the order of unity. L_ex can be expressed as . The critical size of Co-ferrites for the single domain behavior, depending on composition, is between 30 and 70 nm.²⁹ That is, for D ≫ D_Crit, one would expect Hc to decrease by increasing the crystallite size as the system enters the multidomain region. The decrease in Hc is also related to magneto-crystalline anisotropy, the large coercivity in bulk stoichiometric CFO has traditionally been explained by the single-ion anisotropy model, arising from the contribution of the orbital magnetism of Co²⁺ ions at the [B] sites (CoFe₂O₄, high-spin Co²⁺ ions).³⁰ That is, when the Co²⁺ ions migrate from the octahedral sites to the tetrahedral ones because of the variations in the inversion, the coercivity decreases due to the less anisotropic environment of the tetrahedral sites. CFO is only weakly anisotropic at room temperature because of the presence of low-spin Co²⁺ ions. Another reason is the angular momentum of the zinc ion. Zn²⁺ has a zero angular momentum (l = 0) and does not contribute to magneto-crystalline anisotropy; consequently, the magnetic anisotropy and magnetic coercivity will decrease.

3.4 Mössbauer spectroscopy

Mössbauer spectroscopy is a powerful technique to investigate the magnetic properties of magnetic nanoparticles, which depends on various factors viz., particle size, measurement time window and magnetic anisotropy. If the magnetization direction of a magnetic nanoparticle fluctuates in a time greater than 10 ns, Mössbauer platform can detect the presence of magnetic hyperfine field and correspondingly a six line pattern has been generated. On the other hand, when the time of fluctuation τ is less than 10 ns, the time average of the hyperfine field created by the magnetic moment at the nuclear site becomes zero over the measurement time of the Mössbauer effect and consequently the Mössbauer spectrum will be double corresponding to the quadrupole splitting of the ⁵⁷Fe nucleus.^31,32 Mossbauer spectra of all the samples are presented in Fig. 12.

Fig. 12 Room temperature Mossbauer spectra of all the samples of CoZn_xTi_xFe_2−2xO₄.

The Mössbauer spectrum of the sample x = 0.0 exhibit normal Zeeman split two sixtet along with a very week signature of doublet pattern in the central region. Among the two sixtet one due to the Fe³⁺ ions at the tetrahedral A-sites, the other due to the Fe³⁺ ions at the octahedral B-sites. The observed Mössbauer pattern also indicates that the nanoparticles are in the ordered ferrimagnetic state. The presence of the low intense doublet for x = 0.0 could be interpreted by the presence of a small fraction of super-paramagnetic phase, perhaps due to a bilobar size distribution of ferrite particles. The sample with x = 0.4; Mössbauer spectrum consists of doublet and week sextet patterns and shows a relaxation behavior. The primary features of the relaxation spectrum for a magnetically ordered system are a significant broadening of Zeeman lines and a growth of the inner lines arise expense of the outer lines. For x = 0.4, the A site magnetic ion concentration is near to the site percolation threshold for the A site; this effect may be because of the presence of finite clusters together with an infinite magnetic network. The week sextet pattern in this sample indicates the presence of a small fraction of magnetic ordered particles and the intense doublet pattern indicates that the majority of particles are ultrafine particles with either superparamagnetic or paramagnetic behavior. A superimposed quadrupole doublet for x = 0.4, indicating a canted ferromagnetic structure characterized by a significant reduction of magnetic hyperfine field or by the collapse of sextets. It is worth noticing that, the Mössbauer spectra reveal a relaxation as Zn²⁺–Ti⁴⁺ substitution increases as also evidenced by the increase in linewidth (Γ) of octahedral B-site with increasing Zn²⁺–Ti⁴⁺ substitution. In the presence of a paramagnetic hyperfine interaction, the following two characteristic times have to be considered: the relaxation time of the electron spin (spin–spin and spin-lattice) τ_s and the nuclear Larmor precession time τ_L. If τ_s ≫ τ_L, a ‘static’ nonvanishing hyperfine interaction is present at the nucleus and a hyperfine spectrum with sharp lines is expected. If τ_s ≪ τ_L, the hyperfine interaction produces an average value as a result of the rapidly fluctuating electron spins and the splitting collapse. Under the condition τ_s ≈ τ_L, complicated spectra with broad lines are found. This allows an estimation of electron relaxation time to be made.

Quadrupole splitting (QS). The values of QS as obtained from Mössbauer spectra is depicted in Table 4. The presence of chemical disorder in the spinel structure produces an electric field gradient (EFG) of varying magnitude, direction, sign and symmetry and a resulting distribution in the QS. The EFG at ⁵⁷Fe nucleus arises from the asymmetrical charge distribution surrounding the ion. However, since an Fe³⁺ ion has a half-filled 3d shell (3d⁵), the EFG in this case can arise only from an asymmetric charge distribution surrounding the iron ion. In a cubic system having Fe³⁺ at both A- and B-sites, the A-site shows a QS due to the asymmetric charge distribution from the 12 B-neighbors. Fe³⁺ ion at B-site has trigonal symmetry and therefore B-sublattice exhibits an EFG with its principal component V_zz along the [111] direction. This EFG may arise from departure of the six nearest anion neighbors from their ideal octahedral symmetry and, the non-spherical distribution of charges on the next nearest cation and anion neighbors of the B-site. In the present case nearly zero values of QS within the experimental error is an indication that the cubic symmetry is retained between the Fe³⁺ ions and its surrounding comprising Zn²⁺–Ti⁴⁺ substituted CFO nanoparticles.

Table 4 The relative intensity (RI) in percentage, linewidth (Γ), isomer shift (IS), quadrupole splitting (QS), hyperfine magnetic field (H_hf) and fitting quality (χ²) of tetrahedral and octahedral sites of Fe³⁺ ions for CoZn_xTi_xFe_2−2xO₄ (x = 0.0, 0.1, 0.2, 0.3 and 0.4) ferrite derived from Mössbauer spectra recorded at room temperature. Isomer shift values are relative to Fe metal foil (δ = 0.0 mm s⁻¹). Sextet A: tetrahedral site, Sextet B: octahedral site

(x)	Iron sites	RI (%)	Γ (mm s^−1)	IS (mm s^−1)	QS (mm s^−1)	H hf (tesla)	χ ^2
0.0	Doublet	0.65	0.486344 (±0.30613)	0.248804 (±0.06177)	0.220520 (±0.20587)		1.47
	Sextet A	66.79	0.303150 (±0.01942)	0.160103 (±0.00292)	−0.015068 (±0.00482)	49.251087 (±0.01752)
	Sextet B	32.55	0.345018 (±0.03291)	0.438774 (±0.00719)	0.148615 (±0.01234)	50.252955 (±0.05037)
0.1	Sextet A	58.55	0.369817 (±0.04594)	0.263995 (±0.00410)	−0.011570 (±0.00728)	47.960246 (±0.04925)	1.19
	Sextet B	41.45	0.694491 (±0.08087)	0.341672 (±0.01697)	−0.065510 (±0.03088)	51.688579 (±0.43506)
0.2	Sextet A	43.95	0.286968 (±0.03970)	0.265465 (±0.00397)	0.014301 (±0.00769)	46.542426 (±0.05137)	1.21
	Sextet B	56.05	0.773426 (±0.04485)	0.326947 (±0.01238)	−0.038131 (±0.02337)	54.413692 (±0.28624)
0.3	Sextet A	38.60	0.230000 (±0.00000)	0.310329 (±0.00836)	0.001764 (±0.01613)	43.774676 (±0.11353)	1.26
	Sextet B	61.40	1.036929 (±0.05963)	0.379229 (±0.02182)	−0.001109 (±0.04148)	37.016382 (±0.37511)
0.4	Doublet	9.02	0.428724 (±0.01903)	0.348579 (±0.00564)	0.483531 (±0.00949)		0.94
	Sextet A	16.22	0.230000 (±0.0000)	0.265474 (±0.02325)	0.059268 (±0.04536)	43.324537 (±0.30949)
	Sextet B	74.74	0.801281 (±0.07384)	0.366924 (±0.02303)	0.042567 (±0.04260)	37.280437 (±0.36079)

---

Hyperfine magnetic field (H_hf). The Mössbauer study is also crucial to draw any quantitative conclusions regarding the distribution of hyperfine fields (H_hf) at A- and B-site, which is imperative for in depth analysis of magnetic interactions of these materials. In general the hyperfine field is given as:³³

H_hf = H_core + H_STHF + H_THF + H_D (9)

where H_core is the field due to the polarization of core s-electrons, H_THF is the transferred hyperfine fields, H_D is the dipolar field contribution and H_STHF is the supertransferred field associated. The H_STHF at site-A is due to the spin transfer from the d-orbitals of the nearest neighbor cation sites (i.e. belonging to sublattice-B) to the s-orbitals of the ion under consideration at site-A through the ligand anions. Thus STHF at site-A will depend on the magnetic moment of the ions at site-B. In the present case the variation in hyperfine field is due to H_D and H_STHF only because H_core and H_THF do not vary much on changing Zn²⁺–Ti⁴⁺ substitution. The effects due to H_D are also negligible and they mainly cause the line broadening. In light of this, the eqn (9) gets modified as; H_hf = H_STHF.^34,35 From Table 4 small variation in H_hf distribution at A- and B-site is observed. This reflects that H_hf at A-site is not much sensitive to any change in the number and kind of cations at B-site. Thus the changes in H_hf are mainly due to the non-dynamical effects arising from the supertransferred hyperfine interactions (STHF),^34,36 when the cation's neighbors around Fe ions are changed. STHF components are strongly influenced by the super-exchange coupling and magnetic moments of cations. In CFO with spinel structure, each tetrahedral Fe³⁺ ion has strong super-exchange coupling with 12 neighboring metal ions present on the octahedral sites. The replacement of any of Fe³⁺ ions at A-site with Zn²⁺ and Ti⁴⁺ ions bring small change in super-exchange interaction to cause a significant change in magnetic moments and hence STHF, is responsible for variation in present H_hf at A-site. For octahedral B-site; Fe³⁺ ion is coupled via super-exchange coupling to only 6 neighboring metal ions present at A-site. The replacement of octahedral B-site Fe³⁺ ions by Ti⁴⁺ is generally expected to bring significant changes in STHF and hence H_hf. Though, this explanation is not good enough to understand the observed change in the H_hf at A- and B-site. Therefore, significant canting as discussed above in magnetization results must be taken into consideration for the analysis of H_hf spectra. Since STHF components are assumed to depend upon a collinear spin arrangement and spin canting in the samples is not allowing STHF components to contribute effectively to the resultant H_hf. It is observed from Table 4 that H_hf of octahedral B-site is slightly increased up to x = 0.2 and then decreased further with Zn²⁺–Ti⁴⁺ substitution. Hence it may be concluded that the change in magnetization upon introducing the Zn²⁺–Ti⁴⁺ impurity is not only due to the simple replacement of Fe³⁺ ions by non-magnetic Zn²⁺–Ti⁴⁺ ions but also due to a more complex process which leads to the development of canted spin structure. According to Néel's molecular field model,³⁷ A–B exchange interactions are stronger than that of A–A or B–B interactions. In the above mentioned cation distribution Zn²⁺ and Ti⁴⁺, being diamagnetic, do not take part in the exchange interaction. The Fe_B³⁺–O²⁻–Co_B³⁺ super exchange interaction is weaker than the Fe_B³⁺–O²⁻–Fe_B³⁺ interaction. The net magnetic field is mainly due to average Fe_B³⁺–O²⁻–Fe_B³⁺ magnetic bonds per Fe³⁺ ions. The observed behavior in the present case is assigned to the dominance of Fe_B³⁺–O²⁻–Fe_B³⁺ interactions and large occupancy of Zn²⁺ ions at A-site. Further, it can be argued that the entry of Ti⁴⁺ in the lattice causes orientational relaxation of the spins thereby modifying the strength of the exchange interactions.³⁸ The decrease in H_hf for x > 0.2 is due to the larger occupancy of Ti⁴⁺ ions at B-sites. Also the replacement of Fe³⁺ (5 μ_B) ions with non magnetic Zn²⁺–Ti⁴⁺ (0 μ_B) ion reduces the strongest Fe_A³⁺–O²⁻–Fe_B³⁺ interactions and hence H_hf is expected to decrease at higher Zn²⁺–Ti⁴⁺ substitution level. These results are also well supported by Rietveld refined cation distribution and magnetization results.

Isomer shift (IS). Table 4 represents the variation of the isomer shift as a function of x, for Fe³⁺ ions at tetrahedral A- and octahedral B-sites. It is observed that IS at B-site is greater than IS at A-site, this could be interpreted as being due to the large band separation of Fe³⁺–O²⁻ for the octahedral ions compared with that for the tetrahedral ions. As the orbitals of the Fe³⁺ and O²⁻ ions do not overlap, the co-valency effect becomes smaller, and hence the isomer shift is large at the octahedral site. IS at A and B-site appear no significant variation with Zn²⁺–Ti⁴⁺ substitution, thus indicating that the s-electron charge distribution of the Fe³⁺ ions is not influenced by Zn²⁺–Ti⁴⁺ substitution. The range of values of isomer shift indicates that iron exists in Fe³⁺ valence state with high spin configuration in the prepared samples.

Linewidth (Γ). The linewidth values corresponding to A- and B-sites have been found to increase for B-site from 0.345 to 1.036 mm s⁻¹ and for A-site increased from 0.303 (x = 0.0) to 0.369 (x = 0.1) mm s⁻¹ followed by decreasing trend to 0.230 mm s⁻¹ (x = 0.4) with increasing Zn²⁺–Ti⁴⁺ substitution (Table 4). It has been observed that the linewidths at tetrahedral A-sites are smaller than those at octahedral B-sites for the whole range of Zn²⁺–Ti⁴⁺ substitution. The broadening of linewidths could be attributed to slight changes in the varying environment surrounding Fe³⁺ ions in the same sub lattice; such changes in environment of Fe³⁺ ions would lead to a change in the magnetic field and consequently result in an appreciable broadening of the Zeeman lines. The increased broadening in the lines at B-site with an increase in Zn²⁺–Ti⁴⁺ substitution may be attributed to large number of probable distribution of Zn²⁺–Ti⁴⁺ ions surrounding Fe³⁺ nuclei at B-sites. On the other hand decreasing trend of linewidth for A-site (x ≤ 0.1) is ascribed to the reducing number of Fe³⁺ ions from A-site with every substitution of Zn²⁺–Ti⁴⁺ ions.

4. Conclusions

The XRD analysis showed that the prepared CoZn_xTi_xFe_2−2xO₄ (0 ≤ x ≤ 0.4) samples are the single phase cubic structure. All the samples fitted with Rietveld refinement using FullProf program revealed the existence of cubic structure (space group Fd3m). Lattice constant and particle size of CFO found to increase with Zn²⁺–Ti⁴⁺ substitution. Cation distribution estimated from Rietveld refinement shows Zn²⁺ ions have occupy tetrahedral A-site only whereas Ti⁴⁺ and Co²⁺ ions shows strong preference towards octahedral B-site. Quantitative information on the distribution of local magnetic fields and on the canted spin arrangement of Zn²⁺–Ti⁴⁺ substituted CFO nanoparticles provided by Mössbauer spectroscopy is complemented by investigations of their magnetic behavior on the macroscopic scale. For pure CFO Mössbauer exhibits well defined Zeeman sextet corresponding to tetrahedral and octahedral sites, whereas relaxation behavior is observed for x = 0.4. Hyperfine field shows small variation with Zn²⁺–Ti⁴⁺ substitution, which has been explained in terms of supertransfer hyperfine field interactions and observed significant canting in the samples. Hyperfine field at A-site and saturation magnetization showed increased value for x = 0.2 followed by decreasing trend with Zn²⁺–Ti⁴⁺ substitution. Zn²⁺ ions because of its occupancy towards tetrahedral A-sites have greater impact on the magnetic properties as compared to that of Ti⁴⁺ ions. However the contribution from Ti⁴⁺ for the enhancement in the magnetic properties cannot be neglected. Therefore the variation in magnetic properties of cobalt ferrite is the combined effect of both Zn and Ti ions. Real part of permeability of CFO increased with complete range of Zn²⁺–Ti⁴⁺ substitution.

References

1. B. G. Toksha, S. E. Shirsath, M. L. Mane, S. M. Patange, S. S. Jadhav and K. M. Jadhav, J. Phys. Chem. C, 2011, 115, 20905–20912.
2. K. H. Jani, K. B. Modi, H. H. Joshi, P. D. Babu and S. K. Paranjpe, J. Magn. Magn. Mater., 2004, 280, 334–345.
3. S. K. Gore, R. S. Mane, M. Naushad, S. S. Jadhav, M. K. Zate, Z. A. Alothman and B. K. N. Hui, Dalton Trans., 2015, 44, 6384–6390.
4. V. Georgiadou, C. Kokotidou, B. le Droumaguet, B. Carbonnier, T. Choli-Papadopoulou and C. Dendrinou-Samara, Dalton Trans., 2014, 43, 6377–6388.
5. S. Mohapatra, S. R. Rout, S. Maiti, T. K. Maiti and A. B. Panda, J. Mater. Chem., 2011, 21, 9185–9193.
6. E. D. Solovyova, E. V. Pashkova, V. P. Ivanitski, O. I. Vyunov and A. G. Belous, J. Magn. Magn. Mater., 2013, 330, 72–75.
7. K. Watanabe and J. Kawabe, J. Mater. Chem., 1997, 7, 1797–1800.
8. P. Wartewig, M. K. Krause, P. Esquinazi, S. Rosler and R. Sonntag, J. Magn. Magn. Mater., 1999, 192, 83.
9. X. Batlle, M. Pernet and X. Obradors, in Proceedings ICF-5, India, 1989, p. 423.
10. R. H. Kadam, K. Desai, S. R. Kadam and S. E. Shirsath, Solid State Sci., 2013, 26, 31–37.
11. D. G. Agresti, T. D. Shelfer, Y. K. Hong and Y. J. Paig, IEEE Trans. Magn., 1989, 25, 4069.
12. O. Kubo and E. Ogawa, J. Magn. Magn. Mater., 1994, 134, 376.
13. A. Gonzalez-Angeles, G. Mendoza-Suarez, A. Gruskova, M. Papanova and J. Slama, Mater. Lett., 2005, 59, 26–31.
14. M. A. Ahmed, K. E. Rady and M. S. Shams, J. Alloys Compd., 2015, 622, 269–275.
15. B. D. Cullity, Elements of X-ray diffraction, Addison-Wesley Publ. Comp. Inc., Reading, Massachusetts, USA, 1956, p. 99.
16. S. E. Shirsath, S. S. Jadhav, B. G. Toksha, S. M. Patange and K. M. Jadhav, J. Appl. Phys., 2011, 110, 013914.
17. G. Gavollie and J. Hubsch, J. Magn. Magn. Mater., 1983, 36, 304.
18. S. E. Shirsath, M. L. Mane, Y. Yasukawa, X. Liu and A. Morisako, Phys. Chem. Chem. Phys., 2014, 16, 2347.
19. A. Globus, P. Duplex and M. Guyot, IEEE Trans. Magn., 1971, 7(3), 617–622.
20. A. Globus and P. Duplex, J. Appl. Phys., 1968, 39, 727–729.
21. J. Smit and H. P. J. Wijn, Ferrites, Philips Technical Library, Einthoven, Netherland, 1959, p. 275.
22. S. Chikazumi, Physics of Magnetism, Wiley, New York, 1964, p. 263.
23. A. Lakshman, P. S. V. Subba Rao and K. H. Rao, J. Magn. Magn. Mater., 2004, 283, 329–334.
24. V. T. Zaspalis, E. Antoniadis, E. Papazoglou, V. Tsakaloudi, L. Nalbandian and C. A. Sikalidis, J. Magn. Magn. Mater., 2002, 250, 98–109.
25. L. Néel, Acad. Sci., Paris, C. R., 1950, 230, 375.
26. Y. Yafet and C. Kittel, Phys. Rev., 1952, 87, 290–294.
27. W. F. Pong, Y. K. Chang, M. H. Su, P. K. Tseng, H. J. Lin, G. H. Ho, K. L. Tsang and C. T. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 11409–11413.
28. Q. Zeng, I. Baker, V. McCreary and Z. Yan, J. Magn. Magn. Mater., 2007, 318, 28–38.
29. A. E. Berkowitz and W. J. Schuele, J. Appl. Phys., 1959, 30, S134.
30. G. Salazar-Alvarez, R. T. Olsson, J. Sort, W. A. A. Macedo, J. D. Ardisson, M. D. Baró, U. W. Gedde and J. Nogues, Chem. Mater., 2007, 19, 4957–4963.
31. S. Morup, in Science & Technology of Nanostructured Magnetic Materials, ed. G. C. Hadjipanayis and G. A. Prinz, Plenum, NY, USA, 1991, p. 545.
32. S. Sutradhar, S. Pati, S. Acharya, S. Das, D. Das and P. K. Chakrabarti, J. Magn. Magn. Mater., 2012, 324, 1317–1325.
33. W. Marshal, Phys. Rev., 1958, 110, 1280–1285.
34. L. K. Leung, B. J. Evans and A. H. Morrish, Phys. Rev. B: Solid State, 1973, 8, 29–43.
35. D. Peddis, N. Yaacoub, M. Ferretti, A. Martinelli, G. Piccaluga, A. Musinu, C. Cannas, G. Navarra, J. M. Greneche and D. Fiorani, J. Phys.: Condens. Matter, 2011, 23, 426004.
36. G. A. Sawatzky, F. V. D. Woude and A. H. Morrish, J. Appl. Phys., 1968, 39, 1204–1206.
37. L. Néel, Ann. Phys., 1948, 3, 137.
38. P. Chand, R. C. Srivastava and A. Upadhyay, J. Alloys Compd., 2008, 460, 108–114.

---