DOI:
10.1039/C5RA20922F
(Paper)
RSC Adv., 2015,
5, 93139-93146
Scaling of optical forces on Au–PEG core–shell nanoparticles
Received
9th October 2015
, Accepted 23rd October 2015
First published on 26th October 2015
Abstract
Optical trapping of hybrid core–shell gold–polymer particles is studied. Optical forces are measured for different gold core size and polymer shell thickness, revealing how a polymer shell increases the trapping efficiency with respect to the bare gold nanoparticles. Data are in agreement with calculations of optical trapping based on electromagnetic scattering theory in the T-matrix approach. The scaling behaviour of optical forces with respect to the ratio between polymer layer thickness and the whole particle radius is found and discussed.
1 Introduction
Noble metal nanostructures have attracted much attention due to their unique interaction with light, resulting in the collective coherent oscillations (plasmon resonances) of their free electrons and the consequent enhanced material optical properties.1 Colloidal gold nanoparticles (AuNPs) and nanoaggregates are frequently employed in biological applications2,3 because they are non-toxic for cells. Moreover, plasmon resonances can be excited by visible or near-infrared (NIR) wavelengths which penetrate deep into the tissues.4 The surface of gold nanostructures is chemically reactive and, in particular, it binds amine and thiol groups,5 allowing AuNP surface functionalization with different biological stabilizing agents. This property has permitted rapid progress in the development of biocompatible multifunctional particles as, for example, core–shell systems based on AuNPs coated by specific polymers.6,7 In particular, hybrid structures consisting of AuNPs coated by polyethylene glycol (PEG) are currently studied in a broad range of biomedical applications.4,8–12 PEG gives to AuNPs a ‘stealth’ character, i.e., it shields AuNPs to immune system, avoiding the interaction with the proteins responsible for immune system attack. For this reason, AuNPs circulation time in blood increases, leading to their enhanced upload in cancerous or tumorous tissue or cells.10–12
Optical trapping and manipulation of metal nanoparticles has acquired increasing interest in recent years.13–16 Spherical,17–21 non-spherical,22–25 and aggregated26,27 metal particles have been trapped and manipulated in water and, more recently, in air.28 Intriguing applications of optical forces on metal particles, such as plasmonic sorting,29 optical force lithography,30,31 or surface-enhanced spectroscopy,32,33 have been demonstrated. Stable optical trapping of nanoparticles occurs when forces due to high illumination gradients (gradient forces), pointing towards the focus of a tightly focused laser beam, are stronger than the destabilizing effect of radiation pressure (scattering forces), which tends to push the particles along the beam propagation direction (Fig. 1a), and thermal fluctuations.16 The high polarizability of metal nanostructures allows the trapping of particles as small as 10 nm in size.20 However, increased absorption and scattering near plasmon resonances may weaken the trap because of the enhanced radiation pressure. Thus, when trapping metal nanoparticles, it is crucial to find strategies to increase gradient forces in order to overwhelm the detrimental effect of thermal fluctuations, while maintaining an acceptably low radiation pressure.
 |
| | Fig. 1 (a) Sketch of the optical trapping of core–shell systems. Optical tweezers operate at 830 nm with an oil immersion objective (NA = 1.3) to ensure a tight focusing and a stable three-dimensional trapping. Images are not to scale. (b and c) TEM images of 11 nm and 28 nm core radius Au particles, respectively. Scale bar corresponds to 50 nm. (d) Histograms of core radii distribution. (e) Extinction spectra of both 11 nm (red curve) and 28 nm (blue curve) core radius Au particles in aqueous solution. | |
In this scenario, we investigate optical trapping of hybrid core–shell Au–PEG nanoparticles at varying PEG layer thickness. In particular, here we study optical forces on two different series of gold core particles (11 nm and 28 nm in radii) coated by a PEG layer with thickness d ranging from 3 nm to 40 nm, aiming at clarifying the role of the dielectric coating on the trapping of the hybrid Au–PEG structure. Experimental results are also compared with exact calculations of the light scattering process in the T-matrix approach for stratified spheres. A general scaling behavior of optical trapping forces with shell thickness is discussed.
2 Experimental
Core–shell Au–PEG nanoparticles are produced by using both laser-ablated (Laser Ablation Synthesis in Solution, LASiS)34–36 and commercially available Au cores to which PEG coatings at increasing molecular weights have been applied (see Methods). It is worth noting that gold cores have been obtained in ‘clean’ media,35 which maintain AuNP surface available to functionalization with thiolated PEG.
Both dispersions of AuNPs are characterized to evaluate the shape and the size distribution by UV-Visible spectroscopy with a Varian Cary 5 spectrophotometer (2 mm optical path quartz cell). Transmission Electron Microscopy (TEM) analysis is performed with a FEI Tecnai G2 12 operating at 100 kV and equipped with a TVIPS CCD camera. The samples for TEM analysis are prepared by evaporating NPs suspensions on a copper grid coated with an amorphous carbon holey film. TEM images show that both types of nanoparticles have a regular spherical shape (Fig. 1b and c). From the statistical analysis of these images, a narrow size distribution of core radii (Fig. 1d) is obtained. In particular, AuNPs obtained by LASiS have a smaller radius (r ∼ 11 nm) than purchased AuNPs (r ∼ 28 nm). UV-Visible spectra of both types AuNPs show very narrow peaks connected to their narrow distribution of radii (Fig. 1e). As expected, the smaller size AuNPs show a dipolar plasmon peak at approximately 520 nm (red curve), whereas larger particles show a red-shifted plasmon peak at 535 nm (blue curve). However, in both cases, the trapping wavelength, 830 nm, is far detuned to the long-wavelength side of the plasmon resonance.
After the complete size distribution characterization, Au cores are coated by PEG. Thiolated polyethyelene glycols (800, 5000 or 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, from Laysan Bio) are dissolved in distilled water and added to AuNPs dispersions, with final concentration 10−4 M of polymers and 2 × 10−4 M of Au atoms to obtain core–shell systems of Au–PEG nanoparticles (see sketch in Fig. 1a). Finally, the core–shell nanoparticle radius, R, is evaluated by dynamic light scattering measurements. The thicknesses estimated for 800, 5000 and 20
000 Da, from Laysan Bio) are dissolved in distilled water and added to AuNPs dispersions, with final concentration 10−4 M of polymers and 2 × 10−4 M of Au atoms to obtain core–shell systems of Au–PEG nanoparticles (see sketch in Fig. 1a). Finally, the core–shell nanoparticle radius, R, is evaluated by dynamic light scattering measurements. The thicknesses estimated for 800, 5000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da PEG layers are d = 3, 12 and 40 nm, respectively with an uncertainty of about 20%.
000 Da PEG layers are d = 3, 12 and 40 nm, respectively with an uncertainty of about 20%.
Optical trapping experiments are carried out in an inverted microscope setup by focusing a 830 nm laser beam from a diode laser source (Sanyo DL-8032-01) through a high numerical aperture objective (Olympus, Uplan FLN 100X, NA = 1.3). Samples are placed in a small chamber with 75 μL volume attached on the microscope stage. A CCD camera is used to collect the images of the trapped particles. The laser power after the objective, about 26 mW, is kept unchanged during the optical force measurements. Particles are trapped at approximately 4–6 μm from the coverslip. Particle tracking and force measurements are obtained by back focal plane interferometry,37,38 i.e., by imaging the microscope condenser back focal plane onto a quadrant photodiode (QPD). The analog outputs from each quadrants are combined to generate voltage signals proportional to the spatial displacements x, y, z of the trapped particle. Tracking signals are acquired at 65 kHz sampling rate by an acquisition board.
3 Results and discussion
3.1 Optical trapping measurements
Exemplar tracking signals arising from the thermal fluctuations of optically trapped Au–PEG particles with 11 nm core radius and increasing PEG layer thickness are shown in Fig. 2a. From these data it is clearly observed that at increasing PEG shell thickness, the signal amplitude, which is connected to the particle confinement in the trap, decreases as a consequence of a stronger trapping potential.
 |
| | Fig. 2 Tracking signals of Au–PEG nanoparticles (11 nm core radius) at increasing PEG layer thickness (a) and corresponding autocorrelation functions (b). For both graphs color code for data is blue for bare particles, red for 3 nm, green for 12 nm, magenta for 40 nm PEG layer thickness, respectively. | |
The detection of thermal fluctuations is the key in force sensing with optical tweezers.16 Since for small displacements, a trapped particle is subject to a harmonic restoring force, we can exploit a Langevin analysis of the thermal dynamics in the trap to obtain trap calibration and force measurements. Thus, we model the trapped particle positional fluctuations with the overdamped Langevin equation:38
| |
 | (1) |
where
xi is the particle displacement,
ωi =
κi/
γ is the relaxation rate in the confining harmonic potential,
κi are the trap spring constants,
γ = 6π
ηR is the viscous damping,
R is the particle hydrodynamic radius, and
ξi(
t) are random uncorrelated fluctuations with a zero mean value, 〈
ξi(
t)〉 = 0,
δ-like time correlations:
| | |
〈ξi(t)ξi(t + τ)〉 = 2Dδ(τ),
| (2) |
where
D =
κBT/
γ is the diffusion coefficient.
Relaxation rates ωi and, consequently, κi, are obtained by fitting the positional autocorrelation functions38 (ACFs):
| |
 | (3) |
where the exponential decay with lag time
τ is a consequence of the overdamped Langevin equation (
eqn (1)). In
Fig. 2b the normalized ACFs obtained for different layer thickness of Au–PEG hybrid particles with 11 nm core radius are shown. We observe that relaxation rates, and thus, trap force constants, increase (from blue curve to magenta curve) at increasing PEG layer thickness. Note that even though we have a slower thermal diffusion for larger particles,
i.e., for thicker PEG layers, the increase in optical trapping forces yields an increase of the ACFs decay rate that is much larger that any (slowing) diffusion effect. We can then see the increase of optical forces given by the PEG addition directly on the tracking signals (
Fig. 2a) and the ACFs data (
Fig. 2b).
To further analyze the dependence of the spring constants on the core–shell particle structure, larger Au core particles coated by the same PEG shells have been studied. Fig. 3 shows the measured spring constants, normalized to the optical power, as a function of the PEG shell thickness, for both particle cores. Experimental data for the three spatial directions and for both core particles are plotted on a logarithmic scale so that all data can be easily visualized and compared with exact electromagnetic calculations (lines) with no free parameters (see Methods). The uncertainty, mostly related to the core distribution size, represent the standard deviation from the mean value averaged over ten different particles.
 |
| | Fig. 3 Trap spring constants κx (square), κy (triangles), and κz (circles) normalized to trap power measured on Au–PEG particles for the two core radii used, 11 nm (red) and 28 nm (blue). The uncertainty on the data points is the standard deviation from the mean value averaged over ten different particles. Lines are the corresponding values obtained with exact calculations, with no free parameter, of the light scattering process in the T-matrix approach and the reconstruction of the focal spot through the angular spectrum representation. | |
Experimental points obtained on smaller core particles (r = 11 nm, red data) show a clear increase of spring constants with shell thickness, up to more than a sixfold increase for the particles with the thicker shell. Instead, for particles with larger core (r = 28 nm, blue data) such increase is less evident. However, the beneficial effect of the PEG layer is consistently confirmed by a twofold increase of the optical trapping forces. Indeed, it is reasonable to guess that the optical force increase is related to the relative weight of the shell thickness, d, on the whole particle radius, R = d + r, which is lower in particles with larger core.
3.2 Optical trapping calculations
To understand the experimental results, we calculate optical trapping forces by solving the electromagnetic scattering problem in the T-matrix approach for the tightly focused fields.39–42 First, focal fields are calculated by means of the angular spectrum representation.43,44 The total fields are the superposition of incident and scattered fields, and the latter are obtained from the former through the Transition matrix after an appropriate multipole expansion16,45 (see Methods). Then, optical forces are obtained by integrating the averaged Maxwell stress tensor in the far field.16,45 The Au–PEG nanoparticles are modeled as core–shell structures using the Wyatt approach for layered spheres.45,46 The optical constants of the gold core are obtained from the work by Johnson and Christy,47 while for the dielectric shell a refractive index of an hydrated PEG layer is considered, nshell = 1.3995. Exact calculations of optical forces are reported in Fig. 4. This shows that both Au–PEG core–shell particles with small and large core can be stably trapped as we get a negative slope (from which we extract the force constants, κ) of the trapping efficiency Q = cFrad/nmP, where Frad is the radiation force, c the speed of light, nm the medium (water) refractive index, and P the laser beam power. Particles with smaller core (Fig. 4a) present the greatest increase in Q at increasing PEG layer thickness. Thus, the simple addition of a PEG layer appears to improve trapping efficiencies of small metal particles. However, in particles with larger core (Fig. 4b), all curves are comparable and optical forces appear not be largely affected by the PEG layer thickness in the investigated thickness range.
 |
| | Fig. 4 Calculated trapping efficiency for Au–PEG core–shell nanoparticles with r = 11 nm core radius (a) and r = 28 nm core radius (b) at increasing PEG layer thickness. Blue lines represent calculations for bare gold particles, red lines correspond to hybrid particles with 3 nm, green lines with 12 nm, magenta with 40 nm PEG layer thickness, respectively. | |
3.3 Scaling behaviour
In Fig. 5 we summarize our results by studying the scaling behaviour of trapping forces. Here, the trap spring constants, κi (i = x, y, z), normalized to the corresponding values measured on bare AuNPs, κ0i, are shown as a function of the ratio, d/R, between PEG layer thickness and total particle radius. Red and blue open stars are the values obtained by the exact T-matrix calculations. Instead, the black dashed line represents the estimate of the κ/κ0 ratio based on a simple dipole approximation16,48,49 by considering the change in the core–shell particle polarizability as (see Methods):| |
 | (4) |
 |
| | Fig. 5 Trap spring constants κx, κy and κz normalized to the corresponding values, κ0x, κ0y, κ0z, obtained on bare Au core particles, as a function of the ratio, d/R, between PEG layer thickness and total particle radius. Red and blue open stars are the values obtained by the exact T-matrix calculations. Black dashed line represents the estimate of the κ/κ0 ratio based on dipole approximation. | |
The agreement between scaled data and theoretical models is excellent, further confirming the beneficial effect of PEG layer on the stable trapping of small gold nanoparticles and showing that the change in particle polarizability for increasing PEG layer is the main reason for the optical force increase at NIR trapping wavelengths and for spherical shape of the core particle.
4 Conclusions
In conclusion, we have studied the optical trapping of hybrid core–shell Au–PEG nanoparticles. In particular, we focused our attention on the variation of trapping forces induced by the addition of a PEG coating with increasing thickness. We observed that optical trapping forces increase with the increasing thickness of PEG layer. We showed that this enhancement is crucially dependent on the relative weight of the PEG layer polarizability to the total core–shell one. Our study is generic and opens perspectives for the controlled engineering of optical forces on complex hybrid nanosystems were a plasmonic core (of any shape) is combined with a dielectric shell that can be functionalized. Thus, hybridization of optical forces can occur by coupling plasmons and excitons in these engineered core–shell systems.50
5 Methods
5.1 Gold nanoparticle synthesis
Core–shell Au–PEG nanoparticles are produced by using both laser-ablated and commercially available Au cores to which a PEG coating at increasing molecular weights is applied. The aqueous dispersions of AuNPs with r = 11 nm are obtained in two steps by laser ablation synthesis in solution (LASiS) followed by selective sedimentation.34–36 LASiS is performed with 1064 nm (6 ns, 50 Hz, 5 J cm−2) laser pulses of a Nd:YAG laser focused by a f = 15 cm lens on a Au bulk target (99.9% purity) placed at the bottom of a cell containing the liquid. For selective sedimentation, the Au aqueous dispersion is centrifuged in 1.5 mL plastic centrifuge tubes, each filled with 1 mL of nanoparticle solution. We use an Eppendorf centrifuge model 5430 equipped with a fixed angle rotor model FA-45-24-11-HS. Solutions are centrifuged at 200 rcf for 1 hour, then the surnatant is collected and centrifuged again at 300 rcf for 1 hour and then the deposit is collected and re-dispersed in distilled water. The aqueous dispersions of AuNPs with r = 28 nm are commercially available and purchased from British Biocell International.
5.2 Normalized spring constant in dipole approximation
The optical force FDA experienced by a sphere illuminated by a monochromatic field Ei(r, t) = Re{Ei(r)exp(−i2πc/λt)}, in the limit of particle size much smaller than the wavelength λ (dipole approximation) is48,49| |
 | (5) |
where α′ is the real part of the particle polarizability, σext is the extinction cross-section, Si is the Poynting vector and sd is the time-averaged spin density of the incoming wave.49
The first term in eqn (5) is the gradient force, which is responsible of confinement in optical tweezers. The second term is the scattering force, which tends to push particles away from the optical trap. The third term, the spin–curl force, arises only if the polarization of the beam is inhomogeneous.
Our optical tweezers operates in water with a high-numerical aperture objective (NA = 1.3) overfilled by a Gaussian beam. Thus, the spin-curl force is null and the scattering force is small compared to the gradient force. The incident light intensity in the medium is 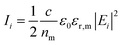 , and the first term in eqn (5) becomes
, and the first term in eqn (5) becomes
| |
 | (6) |
where
| |
 | (7) |
is the real part of the Clausius–Mossotti polarizability in a medium,
nm is the medium refractive index,
V is the particle volume,
εr,p and
εr,m are the relative dielectric permittivity of particle and medium, respectively, and
ε0 is the vacuum dielectric permittivity.
Considering a Gaussian laser beam, the light intensity distribution as a function of the radial coordinate ρ in the transverse plane is
| |
 | (8) |
where
w0 is the beam waist,

, and
P is the laser beam power.
Thus, for small displacements from the beam axis the gradient force is approximated by an harmonic force:
with trap spring constant:
| |
 | (10) |
To get the scaling behaviour for the case of our Au–PEG hybrid particles, we consider the spring constants, κ, normalized to the corresponding value, κ0, of the bare (without PEG) Au particle. Since all experimental parameters are the same for hybrid and bare particles, from eqn (10) we obtain that the scaling of κ/κ0 depends only on the ratio between the real part of the hybrid and bare Au particle polarizabilities:
| |
 | (11) |
where we have approximated the hybrid particle polarizability,
αcore–shell, as the sum of both PEG shell and Au core polarizability,
αcore–shell ≈
αcore +
αshell.
By expressing the real part of the polarizabilities in terms of optical constants we obtain that:
| |
 | (12) |
and since the ratio
Vshell/
Vcore can be expressed as a function of the ratio,
d/
R, between the PEG shell thickness and the hybrid particle radius as:
| |
 | (13) |
we finally get the scaling law of the normalized optical trapping force constants as a function the
d/
R ratio:
| |
 | (14) |
Thus, the dashed black line in Fig. 5 of the main text is calculated by substituting the actual values for the particle size and dielectric constants for the hydrated PEG shell, ε′PEG = 1.39952, water, ε′water = 1.3292, and gold core, ε′Au = −26.5732 and ε′′Au = 1.65922, according to Johnson and Christy.47
5.3 T-matrix calculations of optical forces for stratified spheres
We calculate optical trapping forces by solving the electromagnetic scattering problem in the T-matrix approach for the core–shell particle illuminated by the tightly focused fields. First, the optical fields in the focus of the high NA objective lens are calculated by means of the angular spectrum representation as formulated by Richards and Wolf39,43,44 in the absence of any particle. The resulting field is the field incident on the particles, and the radiation force exerted on any particle within the region is calculated by resorting to linear momentum conservation for the combined system of field and particles, that is by integrating the time-averaged Maxwell stress tensor in the far field:39,45| |
 | (15) |
where the integration is over the full solid angle, r is the radius of a large sphere surrounding the particle, and ![[T with combining macron]](https://www.rsc.org/images/entities/char_0054_0304.gif) M is the time-averaged Maxwell stress tensor in the Minkowski form in a homogeneous, linear and non-dispersive medium:
M is the time-averaged Maxwell stress tensor in the Minkowski form in a homogeneous, linear and non-dispersive medium:| |
 | (16) |
where E = E(r) and B = B(r) are the phasors of the total fields, ⊗ indicates dyadic product, I is the dyadic unit, εm is the dielectric permittivity of the medium, and nm is the refractive index of the medium. Since the total fields are the superposition of incident and scattered fields, E = Ei + Es and B = Bi + Bs, the radiation force simplifies as:| |
 | (17) |
The incident and scattered fields are then expanded in vector spherical harmonics regular at the origin, Bessel J-multipoles, and regular at infinity, Hankel H-multipoles, respectively. The expansion amplitudes of the incident fields, W(p)i,lm, are known through the calculation of the focal fields, while the expansion amplitudes of the scattered fields, A(p′)s,l′m′, are related to the incident amplitudes through the T-matrix elements,39,45 T(p′p)l′m′lm:
| |
 | (18) |
with the angular momentum indices
l = 0, 1, … and
m = −
l, …, 0, …,
l, and the indices
p = 1, 2 indicating the parity of the multipoles. In general, the elements of the T-matrix are calculated in a given frame of reference through the inversion of the matrix of the linear system obtained by imposing the fields boundary conditions across the particle surface. The components of the force are obtained by projecting the force vector onto each unit vector,
e.g.,
Fx =
Frad·
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif)
, and calculating the corresponding numerical integral.
39
The core–shell Au–PEG nanoparticles in our experiments are modeled using the Wyatt generalization of Mie theory for radially symmetric spheres.46 If we consider a radially symmetric sphere with radius R and complex refractive index np = np(r), where r is the radial distance from the centre of the sphere, we expand the incident and scattered fields in the region external to the sphere in terms of J-multipoles, with amplitudes W(p)i,lm, and H-multipoles, with amplitudes A(p)s,lm, respectively. Since the medium inside the sphere is not homogenous, the internal fields do not satisfy two independent Helmholtz equations as in standard (for a homogeneous sphere) Mie theory, but rather the coupled equations
| |
 | (19) |
where
κ0 is the wavevector in vacuum. However, because of the spherical symmetry of the particle, the internal fields can still be expanded in a series of vector spherical harmonics (
J-multipoles) by introducing two general radial functions,
Φl(
r) and
Ψl(
r), regular at the origin, so that for any radial dependence of the refractive index, Maxwell's equations ∇·
B = 0 and ∇·
np(
r)
2E = 0 are satisfied. The radial functions must satisfy the following equations
| |
 | (20) |
which can be integrated numerically. As for Mie theory, by imposing the boundary conditions and exploiting the mutual independence of the vector spherical harmonics we obtain, for each
l and
m, four equations among which the amplitudes of the internal fields
W(p)p,lm can be eliminated. Thus, we get the amplitudes of the scattered field in the form
| |
 | (21) |
where
ρm =
nmκ0R,
G(1)l(
κmr) =
κmrΦl(
r),
G(2)l(
κmr) =
κmrΨl(
r), and
μl(
ρ) and
wl(
ρ) are Riccati–Bessel functions and Riccati–Hankel functions, respectively.
We note that, when np(r) ≡ np is constant, eqn (21) reduce to Mie theory solutions. The theory for radially symmetric spheres is easily applied to layered spheres, i.e., spheres composed of concentric homogenous layers of different refractive indices, as the core–shell nanoparticles in our experiments. This is accomplished by placing a thin transition layer at the interface that, for example, it can be defined in the radial interval r− ≤ r ≤ r+ by varying the refractive index from n− to n+ according to the rule
np2(r) = n−2 + (3s2 − 2s3)Δn2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , , |
where Δ
n2 =
n+2 −
n−2 and

. This ensures the preservation of the continuity of the refractive index and its radial derivative between two contiguous layers.
6 Acknowledgements
We acknowledge support from “Programma Operativo Nazionale Ricerca e Competitività” 2007–2013, Project PON01-01322 PANREX, Project PAC02L3-00087 SOCIAL-NANO, and the MPNS COST Action 1205 “Advances in Optofluidics: Integration of Optical Control and Photonics with Microfluidics” and MP1302 “Nanospectroscopy”.
References
- S. A. Maier, Plasmonics: Fundamentals and Applications, Springer, Berlin, 2007 Search PubMed.
- L. A. Austin, M. A. Mackey, E. C. Dreaden and M. A. El-Sayed, Arch. Toxicol., 2014, 88, 1391–1417 CrossRef CAS PubMed.
- P. Ghosh, G. Han, M. de, C. K. Kim and V. M. Rotello, Adv. Drug Delivery Rev., 2008, 60, 1307–1315 CrossRef CAS PubMed.
- C. M. Cobley, J. Chen, E. C. Cho, L. V. Wang and Y. Xia, Chem. Soc. Rev., 2011, 40, 44–56 RSC.
- F. Zhang, M. W. Skoda, R. M. Jacobs, S. Zorn, R. A. Martin, C. M. Martin, G. F. Clark, G. Goerigk and F. Schreiber, J. Phys. Chem. A, 2007, 111, 12229–12237 CrossRef CAS PubMed.
- F. Correard, K. Maximova, M.-A. Estève, C. Villard, M. Roy, A. Al-Kattan, M. Sentis, M. Gingras, A. V. Kabashin and D. Braguer, Int. J. Nanomed., 2014, 9, 5415 CAS.
- H. Otsuka, Y. Nagasaki and K. Kataoka, Adv. Drug Delivery Rev., 2003, 55, 403–419 CrossRef CAS PubMed.
- Q.-Y. Cai, S. H. Kim, K. S. Choi, S. Y. Kim, S. J. Byun, K. W. Kim, S. H. Park, S. K. Juhng and K.-H. Yoon, Invest. Radiol., 2007, 42, 797–806 CrossRef CAS PubMed.
- B. D. Chithrani, A. A. Ghazani and W. C. Chan, Nano Lett., 2006, 6, 662–668 CrossRef CAS PubMed.
- T. Niidome, M. Yamagata, Y. Okamoto, Y. Akiyama, H. Takahashi, T. Kawano, Y. Katayama and Y. Niidome, J. Controlled Release, 2006, 114, 343–347 CrossRef CAS PubMed.
- A. S. Karakoti, S. Das, S. Thevuthasan and S. Seal, Angew. Chem., Int. Ed., 2011, 50, 1980–1994 CrossRef CAS PubMed.
- R. Mout, D. F. Moyano, S. Rana and V. M. Rotello, Chem. Soc. Rev., 2012, 41, 2539–2544 RSC.
- O. M. Maragò, P. H. Jones, P. G. Gucciardi, G. Volpe and A. C. Ferrari, Nat. Nanotechnol., 2013, 8, 807–819 CrossRef PubMed.
- A. S. Urban, S. Carretero-Palacios, A. A. Lutich, T. Lohmüller, J. Feldmann and F. Jäckel, Nanoscale, 2014, 6, 4458–4474 RSC.
- A. Lehmuskero, P. Johansson, H. Rubinsztein-Dunlop, L. Tong and M. Kall, ACS Nano, 2015, 9, 3453–3469 CrossRef CAS PubMed.
- P. H. Jones, O. M. Maragò and G. Volpe, Optical tweezers: Principles and applications, Cambridge University Press, Cambridge, 2015 Search PubMed.
- K. Svoboda and S. M. Block, Opt. Lett., 1994, 19, 930–932 CrossRef CAS PubMed.
- P. M. Hansen, V. K. Bhatia, N. Harrit and L. Oddershede, Nano Lett., 2005, 5, 1937–1942 CrossRef CAS PubMed.
- Y. Seol, A. E. Carpenter and T. T. Perkins, Opt. Lett., 2006, 31, 2429–2431 CrossRef CAS PubMed.
- F. Hajizadeh and S. N. Reihani, Opt. Express, 2010, 18, 551–559 CrossRef CAS PubMed.
- A. Lehmuskero, R. Ogier, T. Gschneidtner, P. Johansson and M. Kall, Nano Lett., 2013, 13, 3129–3134 CrossRef CAS PubMed.
- C. Selhuber-Unkel, I. Zins, O. Schubert, C. Sonnichsen and L. B. Oddershede, Nano Lett., 2008, 8, 2998–3003 CrossRef CAS PubMed.
- Z. Yan, M. Pelton, L. Vigderman, E. R. Zubarev and N. F. Scherer, ACS Nano, 2013, 7, 8794–8800 CrossRef CAS PubMed.
- O. Brzobohatỳ, M. Šiler, J. Trojek, L. Chvátal, V. Karásek, A. Paták, Z. Pokorná, F. Mika and P. Zemánek, Sci. Rep., 2015, 5, 8106 CrossRef PubMed.
- E. Messina, M. G. Donato, M. Zimbone, R. Saija, M. A. Iatì, L. Calcagno, M. E. Fragala, G. Compagnini, C. D'Andrea, A. Foti, P. G. Gucciardi and O. M. Maragò, Opt. Express, 2015, 23, 8720–8730 CrossRef CAS PubMed.
- P. H. Jones, F. Palmisano, F. Bonaccorso, P. G. Gucciardi, G. Calogero, A. C. Ferrari and O. M. Maragó, ACS Nano, 2009, 3, 3077–3084 CrossRef CAS PubMed.
- E. Messina, E. Cavallaro, A. Cacciola, M. A. Iatì, P. G. Gucciardi, F. Borghese, P. Denti, R. Saija, G. Compagnini, M. Meneghetti, V. Amendola and O. M. Maragò, ACS Nano, 2011, 5, 905–913 CrossRef CAS PubMed.
- L. Jauffred, S. M.-R. Taheri, R. Schmitt, H. Linke and L. B. Oddershede, Nano Lett., 2015, 15, 4713–4719 CrossRef CAS PubMed.
- M. Ploschner, T. Cizmar, M. Mazilu, A. Di Falco and K. Dholakia, Nano Lett., 2012, 12, 1923–1927 CrossRef CAS PubMed.
- M. J. Guffey and N. F. Scherer, Nano Lett., 2010, 10, 4302–4308 CrossRef CAS PubMed.
- S. Nedev, A. S. Urban, A. A. Lutich and J. Feldmann, Nano Lett., 2011, 11, 5066–5070 CrossRef CAS PubMed.
- F. Svedberg, Z. Li, H. Xu and M. Käll, Nano Lett., 2006, 6, 2639–2641 CrossRef CAS PubMed.
- E. Messina, E. Cavallaro, A. Cacciola, R. Saija, F. Borghese, P. Denti, B. Fazio, C. D'Andrea, P. G. Gucciardi, M. A. Iatì, M. Meneghetti, G. Compagnini, V. Amendola and O. M. Maragò, J. Phys. Chem. C, 2011, 115, 5115–5122 CAS.
- V. Amendola and M. Meneghetti, Phys. Chem. Chem. Phys., 2013, 15, 3027–3046 RSC.
- F. Bonaccorso, M. Zerbetto, A. C. Ferrari and V. Amendola, J. Phys. Chem. C, 2013, 117, 13217–13229 CAS.
- V. Amendola, S. Scaramuzza, S. Agnoli, S. Polizzi and M. Meneghetti, Nanoscale, 2014, 6, 1423–1433 RSC.
- F. Gittes and C. F. Schmidt, Opt. Lett., 1998, 23, 7–9 CrossRef CAS PubMed.
- G. Pesce, G. Volpe, O. M. Maragó, P. H. Jones, S. Gigan, A. Sasso and G. Volpe, J. Opt. Soc. Am. B, 2015, 32, B84–B98 CrossRef CAS.
- F. Borghese, P. Denti, R. Saija and M. A. Iatì, Opt. Express, 2007, 15, 11984–11998 CrossRef PubMed.
- R. Saija, P. Denti, F. Borghese, O. M. Maragó and M. A. Iatì, Opt. Express, 2009, 17, 10231–10241 CrossRef CAS PubMed.
- T. A. Nieminen, N. du Preez-Wilkinson, A. B. Stilgoe, V. L. Loke, A. A. Bui and H. Rubinsztein-Dunlop, J. Quant. Spectrosc. Radiat. Transfer, 2014, 146, 59–80 CrossRef CAS.
- S. Simpson, J. Quant. Spectrosc. Radiat. Transfer, 2014, 146, 81–99 CrossRef CAS.
- B. Richards and E. Wolf, Proc. R. Soc. A, 1959, 253, 358–379 CrossRef.
- A. A. R. Neves, A. Fontes, L. d. Y. Pozzo, A. A. de Thomaz, E. Chillce, E. Rodriguez, L. C. Barbosa and C. L. Cesar, Opt. Express, 2006, 14, 13101–13106 CrossRef PubMed.
- F. Borghese, P. Denti and R. Saija, Scattering from Model Nonspherical Particles, Springer, Berlin, 2007 Search PubMed.
- P. J. Wyatt, Phys. Rev., 1962, 127, 1837–1843 CrossRef CAS.
- P. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370–4379 CrossRef CAS.
- J. R. Arias-González and M. Nieto-Vesperinas, J. Opt. Soc. Am. A, 2003, 20, 1201–1209 CrossRef.
- S. Albaladejo, M. I. Marqués, M. Laroche and J. J. Sáenz, Phys. Rev. Lett., 2009, 102, 113602 CrossRef PubMed.
- A. Ridolfo, et al., ACS Nano, 2011, 5, 7354–7361 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da, from Laysan Bio) are dissolved in distilled water and added to AuNPs dispersions, with final concentration 10−4 M of polymers and 2 × 10−4 M of Au atoms to obtain core–shell systems of Au–PEG nanoparticles (see sketch in Fig. 1a). Finally, the core–shell nanoparticle radius, R, is evaluated by dynamic light scattering measurements. The thicknesses estimated for 800, 5000 and 20
000 Da, from Laysan Bio) are dissolved in distilled water and added to AuNPs dispersions, with final concentration 10−4 M of polymers and 2 × 10−4 M of Au atoms to obtain core–shell systems of Au–PEG nanoparticles (see sketch in Fig. 1a). Finally, the core–shell nanoparticle radius, R, is evaluated by dynamic light scattering measurements. The thicknesses estimated for 800, 5000 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da PEG layers are d = 3, 12 and 40 nm, respectively with an uncertainty of about 20%.
000 Da PEG layers are d = 3, 12 and 40 nm, respectively with an uncertainty of about 20%.



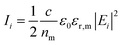 , and the first term in eqn (5) becomes
, and the first term in eqn (5) becomes


 , and P is the laser beam power.
, and P is the laser beam power.






![[T with combining macron]](https://www.rsc.org/images/entities/char_0054_0304.gif) M is the time-averaged Maxwell stress tensor in the Minkowski form in a homogeneous, linear and non-dispersive medium:
M is the time-averaged Maxwell stress tensor in the Minkowski form in a homogeneous, linear and non-dispersive medium:


![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , and calculating the corresponding numerical integral.39
, and calculating the corresponding numerical integral.39



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ,
, . This ensures the preservation of the continuity of the refractive index and its radial derivative between two contiguous layers.
. This ensures the preservation of the continuity of the refractive index and its radial derivative between two contiguous layers.





