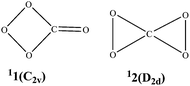
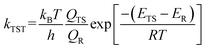Monocyclic and bicyclic CO₄: how stable are they?

Abstract

Seeking promising molecular species with huge energy release and significant kinetic stability continues to be a hot topic and a great challenge in the field of high-energy density materials (HEDMs). CO₄ is the first high-order carboxide that has the potential as an energetic molecule. However, the intrinsic kinetic stability of its two most studied energy-rich isomers, i.e., ¹1 (monocyclic) and ¹2 (bicyclic), has remained quite unclear in spite of numerous studies. This has greatly hindered the quantitative stability assessment of ¹1 and ¹2 under various conditions as well as the justification of their prospect as energetic candidates. In this work, for the first time we report the rate-determining transition states associated with the CO₂-elimination from ¹1 and ¹2. The thermodynamics of ¹1 and ¹2 was described using G3B3, CBS-QB3, G4, W1BD, CCSD(T)/CBS and CASPT2/CBS, while the kinetic stability was analyzed based on broken-symmetry UCCSD(T)/CBS and CASPT2/CBS single-point energy calculations on UB3LYP geometries. The rate-determining barriers for the dissociation of ¹1 and ¹2 into CO₂ + ¹O₂ at 298 K were found to amount to 28.7 and 14.7 kcal mol⁻¹ at the CASPT2(18e,12o)/CBS level of theory, and 23.5 and 21.1 kcal mol⁻¹ at the UCCSD(T)/CBS level of theory, respectively. ¹1 is a kinetically stable energetic molecule, which releases 45.2 kcal mol⁻¹ upon dissociation into CO₂ + ¹O₂ at the CASPT2(18e,12o)/CBS level and 38.9 kcal mol⁻¹ at the UCCSD(T)/CBS level, and could serve as a rigid energetic building block for larger oxocarbons. The bicyclic ¹2 releases much higher energy, 79.3 kcal mol⁻¹ at the CASPT2(18e,12o)/CBS level and 73.4 kcal mol⁻¹ at the CASPT2-corrected UCCSD(T)/CBS level whereas the barrier for dissociation is lower than that of monocyclic ¹1.

---

1. Introduction

High-energy density materials include explosives, propellants, and pyrotechnics, that are used for military purposes and civilian applications. In the development of new HEDMs, a well-known issue is that HEDMs usually have the contradictory requirements of high performance and low sensitivity, which greatly challenges synthetic chemists and theoreticians. The main step to design promising energetic materials is to acquire an effective energetic building unit, which could be further assembled and modified by energetic functional groups.^1–10 Obviously, excellent energetic units played a crucial role in the development of energetic materials.

The oxides of the main group IV element carbon, i.e., CO_n, constitute an important class of compounds. Besides CO and CO₂ that have a well-known direct bearing on human life, the high-order carboxides CO_n (n > 2) have been receiving growing attention in the last decades.^11–25 They can be produced in the reactions of oxygen (atomic or molecular) with the lower oxides of carbon, hydrocarbons, and other organic molecules.²⁶ CO_n and their ions are also relevant to the chemistry of the terrestrial²⁷ and planetary²⁸ atmospheres. Of particular interest, the high-order carboxides possess numbers of single C–O and O–O bonds, which could release a large amount of heat upon transformation to the stable CO, CO₂ and O₂ species. Thus, members of the CO_n family could be potential molecular energetic materials or high-energy density materials (HEDMs), the next generation of environmentally benign propellants and explosives. Due to the energetic feature, the lifetime of CO_n structures should highly rely on their rate-determining barrier heights.

We are particularly interested in carbon tetraoxide (CO₄), which is the first energy-rich CO_n since decomposition of the lower-order CO₃ is endothermic towards the low-energy yet spin-forbidden dissociation into CO₂ + ³O and CO + ³O₂.²⁶ The chemically bound structures of CO₄ were first considered by Averyanov et al. in 1996.¹² They performed thorough thermodynamical calculations on two isomers ¹1 and ¹2 (see Scheme 1),¹² showing their metastability (by 48 and 80 kcal mol⁻¹, respectively). Though no decomposition transition states were located, Averyanov et al. surmised that ¹1 and ¹2 should have large decomposition barriers in the adiabatic pathway.¹² Besides, by analyzing the nonradiative singlet-triplet decay, Averyanov et al. deduced an upper limit for the barrier to the dissociation of ¹2 ranging from 15.0 to 27.3 kcal mol⁻¹.¹³ In 2003, using neutralization-reionization mass spectrometry (NRMS). Cacace and coworkers reported the first detection of neutral CO₄ and, based on their own and previous computational studies, assigned it the bicyclic ¹2 structure with a lifetime exceeding 1 μs in the isolated gas state.¹⁵ Later in 2007, Jamieson et al. reported on the detection of the monocyclic isomer ¹1via low temperature infrared spectroscopy of CO₂ ice.¹⁹ CO₄ has also been the subject of other computational^14,17,23,24 and experimental²⁴ studies. No quantitative estimation of the kinetic stability of ¹1 has been reported.

Scheme 1 Key isomers of CO₄.

Clearly, in spite of the 20 year research history, our knowledge of CO₄ is far from being sufficient. The intrinsic stability of its two most important isomers, i.e., ¹1 and ¹2, still remains undetermined. ¹1 and ¹2 have been previously expected to have large barriers towards the dissociation into ¹O₂ + CO₂. Yet how large can the barriers be? The lack for this crucial information jeopardizes the assessment of CO₄ as a potential energetic material, since a barrier higher than 20 kcal mol⁻¹ has been suggested for suitable candidates for energetic molecules.²⁹ It must also be noted that both the monocyclic and bicyclic CO₄ can be adequately described by single determinantal methods,¹⁷ whereas the CO₂-elimination produces ¹O₂ that is a well-known multi-reference molecule.^30,31

To fill in the gap of the available CO₄ study, for the first time here we have identified the transition states for the CO₂-elimination from ¹1 and ¹2. Our results confirmed previous conjectures that CO₄ does have the possibility to serve as an energetic molecule due to its large rate-determining barrier, although the barrier for the dissociation of the bicyclic ¹2 shows some variations depending on the method used.

2. Computational methods

Firstly, the structures of the singlet isomers, singlet transition states and fragments of CO₄ were obtained at the B3LYP/aug-cc-pVTZ level followed by the frequency calculations to establish their stationary nature. To ensure accurate description of the energies, we applied various theoretical methods: (1) CCSD(T) calculations with the complete basis set (CBS) limit extrapolation based on the CCSD(T)/aug-cc-pVTZ and CCSD(T)/aug-cc-pVQZ energies (denoted as CCSD(T)/CBS//B3LYP/aug-cc-pVTZ). The complete basis set (CBS) limit extrapolation was investigated by Halkier et al., which is guided by r_i,j-dependent methods.³² (2) G3B3,³³ G4,³⁴ CBS-QB3 (ref. 35) and W1BD³⁶ calculations. Note that the connection of each located transition state was checked by the intrinsic reaction coordinate (IRC) method at the B3LYP/6-31G(d) level (starting from the B3LYP/6-31G(d) transition state). To provide accurate spectroscopic properties, the CCSD(T)/aug-cc-pVTZ geometry optimization and frequency calculation were carried out. All the above calculations were performed with the GAUSSIAN03 (ref. 37) and GAUSSIAN09 (ref. 38) packages.

Secondly, for the species ¹O₂, TS1 and TS2 that have significant multi-reference character, we applied the broken-symmetry strategy of Noodleman³⁹ at the B3LYP level, i.e., UB3LYP/aug-cc-pVTZ geometrical optimization with the “guess = (mix, always)” keyword. For the energetics, we applied two kinds of theoretical methods: (1) the complete basis set (CBS) limit extrapolation based on the UCCSD(T)/aug-cc-pVTZ and UCCSD(T)/aug-cc-pVQZ energies (denoted as UCCSD(T)/CBS//UB3LYP/aug-cc-pVTZ), and (2) a modified version of CASPT2 (Complete Active Space with Second-order Perturbation Theory, developed by Celani and Werner,⁴⁰ referred to as ‘RS2C’ in Molpro), which accounts for dynamic correlation, using the CASSCF wave functions as references in the RS2C calculation. Active space includes 18 electrons and 12 active orbitals, namely CASPT2(18e,12o). All CASPT2 calculations were made without symmetry constraints on the wave function. The aug-cc-pVTZ and aug-cc-pVQZ basis sets were used in order to deduce the CBS limit extrapolation for CASPT2(18e,12o) calculations.⁴¹ The combined CASPT2 and UB3LYP studies (i.e., CASPT2//UB3LYP) have been shown to apply well in various systems.^42,43 All the CASPT2 calculations were carried out with the Molpro 2010⁴⁴ program package and the UCCSD(T) method were carried out with the GAUSSIAN09 (ref. 38) program package. Since CASPT2 method can give a better description for reference state system, we chose CASPT2 basis for discussion.

To get the half-life values of ¹1 and ¹2 at different temperatures, we applied the conventional transition state theory (CTST), which was described below. Q_TS, Q_R are the partition functions of the transition state and the reactant, respectively. E_TS and E_R stand for the energy of the transition state and the reactant with ZPVE. The other parameters are k_B for Boltzmann constant, h for Planck constant, T for temperature and R for universal gas constant.

All the above calculations were performed at 298.15 K (temperature) and 1 atm (pressure). The zero-point vibrational energy (ZPVE) was automatically considered in the composite G3B3, G4, CBS-QB3 and W1BD calculations, while in the B3LYP/aug-cc-pVTZ and CCSD(T) studies, the ZPVE from the B3LYP/aug-cc-pVTZ frequency calculation should be manually included (denoted by “+ZPVE”).

3. Results and discussions

The optimized isomers and transition states of CO₄ at the B3LYP/aug-cc-pVTZ level are shown in Fig. 1. For easy discussion, we set the total energy of ¹1 at various computational levels to be zero as reference. The relative energies can be found in Table 1. The wave numbers, rotational constants and dipole moments are given in Table 2. Note that the superscript before a species means the spin multiplicity, i.e., 1 for singlet and 3 for triplet.

Fig. 1 Geometrical parameters (Å) and point group of ¹1, ¹2, ¹TS1, U¹TS1, ¹TS2, U¹TS2 at the B3LYP/aug-cc-pVTZ level. The geometrical parameters in brackets are calculated at the CCSD(T)/aug-cc-pVTZ level.

Table 1 Relative Energies (kcal mol⁻¹) of ¹1, ¹2, U¹TS1, U¹TS2 and products CO₂ + ¹O₂, CO₂ + ³O₂

	^11	^12	U^1TS1 ^b	U^1TS2 ^b	CO2 + ^1O2^b	CO2 + ^3O2
a The relative energy of CO2 + ^1O2 in parentheses was corrected by the CASPT2/CBS single–triplet (S–T) gap of O2 with respect to CO2 + ^3O2 (W1BD), i.e., −39.0 = −61.8 + 22.8. b The energies are from the open shell single-point calculations based on the open shell geometries.
B3LYP/aug-cc-pVTZ+ZPVE	0.0	39.0	20.3	50.8	−57.8	−67.9
G3B3	0.0	33.8				−62.6
CBS-QB3	0.0	33.8				−60.6
G4	0.0	33.3				−61.8
W1BD^a	0.0	34.8			−32.3(−39.0)	−61.8
CCSD(T)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE	0.0	33.8	22.8	53.8	−51.1	−61.0
CCSD(T)/aug-cc-pVQZ//B3LYP/aug-cc-pVTZ+ZPVE	0.0	34.2	23.2	54.8	−51.6	−61.4
CCSD(T)/CBS//B3LYP/aug-cc-pVTZ+ZPVE	0.0	34.5	23.5	55.6	−52.0	−61.7
CASPT2(18e,12o)/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ+ZPVE	0.0	34.2	28.8	46.7	−43.8	−67.1
CASPT2(18e,12o)/aug-cc-pVQZ//B3LYP/aug-cc-pVTZ+ZPVE	0.0	34.1	28.7	47.9	−44.6	−67.6
CASPT2(18e,12o)/CBS//B3LYP/aug-cc-pVTZ+ZPVE	0.0	34.1	28.7	48.8	−45.2	−68.0

---

Table 2 The key spectroscopic parameters including wave numbers M_wav (cm⁻¹), rotational constants R (GHz) and dipole moment D (Debye) of ¹1 and ¹2 at the CCSD(T)/aug-cc-pVTZ level, and the half-life of ¹1 and ¹2 with the barriers at CASPT2(18e,12o)/CBS//UB3LYP/aug-cc-pVTZ level at different temperatures

	M wav (cm^−1)	R (GHz)	D (Debye)	t ^298.15 K1/2 (s)	t ^200 K1/2 (s)	t ^100 K1/2 (s)
^11	287.9
	510.4
	725.8
	773.2	15.18514
	834.3	5.71438	1.2599	4.2 × 10^7	1.5 × 10^18	7.5 × 10^49
	870.0	4.15194
	1015.1
	1160.3
	1979.8
^12	339.5
	540.4
	540.7
	562.8	12.44232
	678.0	5.30909	0.0546	1.2 × 10^−5	4.4 × 10^2	1.3 × 10^21
	989.2	5.30909
	1046.3
	1046.4
	1657.5

---

3.1 Thermodynamics of ¹1 and ¹2

Previous CASSCF calculations have indicated that the single determinantal method should be sufficient to describe ¹1 and ¹2.²⁰ In fact, we found that the T1Diag values of ¹1 and ¹2 are 0.019 and 0.017, respectively, which lie below the threshold 0.02 recommended by Lee.⁴⁵ So we have sufficient confidence to obtain the reliable energetics of ¹1 and ¹2 relative to the global fragments CO₂ + ³O₂ simply based on the single determinantal calculations. As listed in Table 1, ¹1 lies higher in energy than CO₂ + ³O₂ by 62.6 (G3B3), 60.6 (CBS-QB3), 61.8 (G4), 61.8 (W1BD), 61.7 (CCSD(T)/CBS//B3LYP/aug-cc-pVTZ+ZPVE) kcal mol⁻¹. The relative energy between ¹1 and ¹2 is 33.8, 33.8, 33.3, 34.8 and 34.5 kcal mol⁻¹, respectively at the four composite levels and at the CCSD(T)/CBS level. The agreement between these methods is good. We suggest to adopt the most costly W1BD calculations as our recommended values for the thermodynamic properties of ¹1, ¹2 and CO₂ + ³O₂. Interestingly, CASPT2(18e,12o)/CBS//B3LYP/aug-cc-pVTZ+ZPVE predicts the relative energy 34.1 kcal mol⁻¹ between ¹1 and ¹2, which agrees quite well with the composite calculations. Yet, the relative energy of CO₂ + ³O₂, i.e., 68.0 kcal mol⁻¹ at the CASPT2/CBS//B3LYP level, is about 6 kcal mol⁻¹ higher than that predicted by the composite calculations.

As for the energetics of the spin-allowed product CO₂ + ¹O₂, not unexpectedly calculations are problematic at almost all levels of theory, due to the multi-reference character of ¹O₂.²⁰ The G3B3, CBS-QB3, G4, W1BD, CCSD(T)/CBS//B3LYP/aug-cc-pVTZ+ZPVE and UCCSD(T)/CBS//UB3LYP/aug-cc-pVTZ+ZPVE methods consistently give the singlet–triplet (S–T) gap of oxygen as about 29 kcal mol⁻¹, with the exception of the latter that gives the gap as 9.7 kcal mol⁻¹ (see Table 1). Compared to the experimental value of 22.5 kcal mol⁻¹,²¹ all six methods do not give an accurate description. The CASPT2(18e,12o)/CBS//UB3LYP/aug-cc-pVTZ+ZPVE calculation predicts the S–T gap as 22.8 kcal mol⁻¹, excellently matching the experimental value. Therefore, we can use this value, or alternatively the experimental value which is very close, in order to calculate the energy of ¹O₂ with respect to that of the ³O₂ ground state. The best estimate for the relative energy of CO₂ + ¹O₂ is −39.0 (=−61.8 + 22.8) kcal mol⁻¹ at the W1BD level with the CASPT2 correction of the S–T gap of oxygen. As a result, the spin-allowed energy release of ¹1 and ¹2 to CO₂ + ¹O₂ is 39.0 and 73.8 kcal mol⁻¹, at the CASPT2-corrected W1BD level, and 38.9 and 73.4 at the CASPT2-corrected CCSD(T)/CBS level, respectively.

3.2 Kinetics of ¹1 and ¹2

Clearly, ¹1 and ¹2 are energetic species and the lowest energy path to the product CO₂ + ¹O₂ could be the rate-determining step to determine their lifetime of existence. The reactants ¹1 and ¹2 are of the single determinantal type, whereas the product ¹O₂ has significant multi-reference character. So we studied the respective CO₂-elimination transition states TS1 and TS2 using both the restricted and unrestricted wave functions. The former is the same as that applied to ¹1 and ¹2, for which the single determinantal wave function is enough. At the composite G3B3, CBS-QB3, G4, W1BD, CCSD(T)/CBS//B3LYP/aug-cc-pVTZ+ZPVE levels, the CO₂-elimination barrier is higher than 30 kcal mol⁻¹, i.e., 36.9, 37.0, 37.1, 35.2 and 36.6 kcal mol⁻¹ for ¹1, and 35.3, 35.3, 35.0, 30.7 and 34.8 kcal mol⁻¹ for ¹2. Yet the wave functions of ¹TS1 and ¹TS2 have significant internal RHF → UHF instability, and the corresponding T1Diag values are as large as 0.065 and 0.109, greatly exceeding 0.02. Thus ¹TS1 and ¹TS2 should have significant multi-reference nature. To resolve this problem, we adopted the broken-symmetry strategy to optimize ¹TS1 and ¹TS2 at the UB3LYP/aug-cc-pVTZ level. The obtained CO₂-elimination transition states are labeled by U¹TS1 and U¹TS2. Both U¹TS1 and U¹TS2 are subject to severe spin contamination with the 〈S²〉 values 0.84 and 0.85, indicative of the mixing of the higher spin states.

The energetics of U¹TS1 and U¹TS2 were further refined by the multi-reference-based CASPT2(18e,12o) calculations and UCCSD(T) method with the CBS extrapolation based on the aug-cc-pVTZ and aug-cc-pVQZ, CASPT2(18e,12o)//UB3LYP/aug-cc-pVTZ and aug-cc-pVTZ and aug-cc-pVQZ UCCSD(T)//UB3LYP/aug-cc-pVTZ results. In sharp contrast to the restricted calculations, the ZPVE-corrected CO₂-elimination barriers 28.7 and 14.7 kcal mol⁻¹ (viaU¹TS1 and U¹TS2, respectively) at the CASPT2(18e,12o)/CBS level were both much reduced compared to the restricted calculations based on ¹TS1 and ¹TS2 (see ESI Table S1†). At the UCCSD(T)/CBS level of theory the difference between the barriers (i.e. 23.5 and 21.1 kcal mol⁻¹, respectively) for the dissociation of ¹1 and ¹2 is much lower. This is not unexpected since it is well known that CASPT2 can describe very well multi-configurational states, although dynamical correlation effects could be underestimated, while UCCSD(T) describes very well dynamical correlation effects and could underestimate multi-configurational effects. Future study that can properly include the balanced description of both the multi-reference and correlation effects is still desired.

3.3 Implications

After the initiation of the CO₄ study in 1996,¹² here we explicitly determined the CO₂-elimination barrier height that governs the intrinsic stability of the two key cyclic isomers ¹1 and ¹2 for the first time. The spin-allowed exothermicity of 39.0 kcal mol⁻¹ and the fragmentation barrier lying between 28.7 and 23.5 kcal mol⁻¹ showed that ¹1 itself is a kinetically very stable energetic molecule. The dissociation of the bicyclic ¹2 is much more exothermic, 73.8 kcal mol⁻¹, and the CO₂-elimination barrier, lying between 14.7 and 21.1 kcal mol⁻¹ should be close to the conservative value of 20 kcal mol⁻¹ recommended for the dissociation barrier of a HEDM.²⁹ Accordingly, these CO₄ isomers can serve as useful energetic building blocks for the formation of more complex carboxides (i.e., C_mO_n).

By computing the decomposition rate constants based on conventional transition state theory, we determined the half-life values of ¹1 and ¹2 at 100, 200 and 298.15 K (see Table 2). To assist their low-temperature spectroscopic characterization, the wave numbers, rotational constants and dipole moments were also collected in Table 2. The present work focuses on the intrinsic stability of CO₄ against its unimolecular decomposition, which is essential for assessment of an HEDM. Surely, in actual usage, its reactivity towards ambient species (e.g., O₂, H₂O) might need to be investigated. Besides, to see whether in condensed phase, CO₄ can undergo oligomerization, we investigated the head-to-tail and head-to-head cycloaddition reactions at the C=O bond of ¹1. These are both endothermic (i.e., the CO₄ dimer of ¹1 lies 43.9 and 113.5 kcal mol⁻¹ higher than two ¹1, respectively. See ESI1†), clearly showing the low probability for cycloaddition. Finally, since many peroxides (with O–O bonding) can release ³O₂ during the photochemical or basic processes, the 2CO₄ → 2CO₂ + 2³O₂ reaction with large exothermicity seems feasible. Yet such processes usually involve complicated radical or ionic processes, which is out of the present scope. It should be noted that under thermal conditions, when the CO₄ molecules approach each other, the lone pair electrons of oxygen might exert strong repulsion to hinder the approach of each other.

The quantitative intrinsic stability and the detailed vibrational features for the rate-determining CO₂-elimination transition states should be a base for future exploration of its formation and depletion dynamics either in gas phase or on condensed ice surface. Moreover, the present study leads us to predict that in studying the analogous energy-rich carboxides, multi-reference calculations (e.g., CASPT2) are essential for predicting the barrier heights for CO₂ + ¹O₂ elimination, though the single determinantal methods can still be applied to describe the thermodynamic properties of isomers provided a correct scaling for the energy of ¹O₂ with respect to that of ³O₂.

4. Conclusions

CO₄ belongs to the class of potential energy-rich molecules. Yet, despite the 20 year research history, the intrinsic kinetic stability of CO₄, the second member of the higher-order carboxides (CO_n), has remained unclear. In this work, for the first time we have located the transition states for the CO₂-elimination from two key CO₄ isomers ¹1 and ¹2. The rate-determining barriers for ¹1 and ¹2 were computed to be 28.7 and 14.7 kcal mol⁻¹, respectively, at the CASPT2(18e,12o)/CBS//B3LYP/aug-cc-pVTZ+ZPVE level, 23.5 and 21.1 kcal mol⁻¹, respectively, at the UCCSD(T)/CBS//B3LYP/aug-cc-pVTZ+ZPVE level. This work can provide a useful reference for the study of other carboxides C_mO_n.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (No. 21273093, 21473069, 21073074). G. d. P. thanks for the funding of Italian Government FIRB 2010. The authors are very grateful for the reviewers' invaluable comments and suggestions.

References

1. T. T. Vo, J. Zhang, D. A. Parrish, B. Twamley and J. M. Shreeve, J. Am. Chem. Soc., 2013, 135, 11787.
2. C. Li, L. Liang, K. Wang, C. Bian, J. Zhang and Z. Zhou, J. Mater. Chem. A, 2014, 2, 18097.
3. Y. Tang, H. Gao, D. A. Parrish and J. M. Shreeve, Chem.–Eur. J., 2015, 21, 11401.
4. Q. Wu, W. Zhu and H. Xiao, J. Mater. Chem. A, 2014, 2, 13006.
5. R. Haiges, P. Deokar and K. O. Christe, Angew. Chem., Int. Ed., 2014, 126, 5535.
6. R. Haiges, M. Vasiliu, D. A. Dixon and K. O. Christe, Angew. Chem., Int. Ed., 2015, 127, 9229.
7. J. Zhang and J. M. Shreeve, J. Am. Chem. Soc., 2014, 136, 4437.
8. J. Zhang and J. M. Shreeve, J. Phys. Chem. C, 2015, 119, 12887.
9. H. Gao and J. M. Shreeve, Chem. Rev., 2011, 111, 7377.
10. Q. Zhang and J. M. Shreeve, Chem. Rev., 2014, 114, 10527.
11. V. Raducu, D. Jasmin, R. Dahoo, P. Brosset, B. Gauthier-Roy and L. Abouaf-Marguin, J. Chem. Phys., 1994, 101, 1878.
12. A. Averyanov, Y. G. Khait and Y. V. Puzanov, J. Mol. Struct.: THEOCHEM, 1996, 367, 87.
13. A. Averyanov, Y. G. Khait and Y. V. Puzanov, J. Mol. Struct.: THEOCHEM, 1999, 459, 95.
14. J. Song, Y. G. Khait and M. R. Hoffmann, J. Phys. Chem. A, 1999, 103, 521.
15. F. Cacace, G. de Petris, M. Rosi and A. Troiani, Angew. Chem., Int. Ed., 2003, 42, 2985.
16. C. J. Bennett, C. Jamieson, A. M. Mebel and R. I. Kaiser, Phys. Chem. Chem. Phys., 2004, 6, 735.
17. B. M. Elliott and A. I. Boldyrev, J. Phys. Chem. A, 2005, 109, 3722.
18. C. S. Jamieson, A. M. Mebel and R. I. Kaiser, Phys. Chem. Chem. Phys., 2006, 7, 2508.
19. C. S. Jamieson, A. M. Mebel and R. I. Kaiser, Chem. Phys. Lett., 2007, 440, 105.
20. C. S. Jamieson, A. M. Mebel and R. I. Kaiser, Chem. Phys. Lett., 2007, 443, 49.
21. T. Kowalczyk and A. I. Krylov, J. Phys. Chem. A, 2007, 111, 8271.
22. C. S. Jamieson, A. M. Mebel and R. I. Kaiser, Chem. Phys. Lett., 2008, 450, 312–317.
23. R. I. Kaiser and A. M. Mebel, Chem. Phys. Lett., 2008, 465, 1.
24. L. Y. Yeung, M. Okumura, J. T. Paci, G. C. Schatz, J. Zhang and T. K. Minton, J. Am. Chem. Soc., 2009, 131, 13940.
25. K. S. Haygarth, T. W. Marin, I. Janik, K. Kanjana, C. M. Stanisky and D. M. Bartels, J. Phys. Chem. A, 2010, 114, 2142.
26. M. J. Perri, A. L. van Wyngarden, J. J. Lin, Y. T. Lee and K. A. Boering, J. Phys. Chem. A, 2004, 108, 7995.
27. A. Mebel, M. Hayashi, V. Kislov and S. Lin, J. Phys. Chem. A, 2004, 108, 7983.
28. (a) Y. L. Yung, A. Y. Lee, F. W. Irion, W. B. DeMore and J. Wen, J. Geophys. Res., D, 1997, 102, 10857; (b) S. Falcinelli, M. Rosi, P. Candori, F. Vecchiocattivi, J. M. Farrar, F. Pirani, N. Balucani, M. Alagia, R. Richter and S. Stranges, Planet. Space Sci., 2014, 99, 149.
29. G. Chung, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 2000, 104, 5647.
30. C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685.
31. E. A. Lissi, M. V. Encinas, E. Lemp and M. A. Rubio, Chem. Rev., 1993, 93, 6.
32. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243.
33. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650.
34. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108.
35. (a) J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822; (b) J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532.
36. E. C. Barnes, G. A. Petersson, J. A. Montgomery Jr, M. J. Frisch and J. M. L. Martin, J. Chem. Theory Comput., 2009, 5, 2687.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 03, Revision D.02, Gaussian, Inc., Wallingford, CT, 2009.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery JrT. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kita, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cro, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenbe, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2004.
39. (a) L. Noodleman, J. Chem. Phys., 1981, 74, 5737; (b) L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131; (c) A. Ovchinnikov and J. K. Labanowski, Phys. Rev. A, 1996, 53, 3946; (d) C. Adamo, V. Barone, A. Bencini, F. Totti and I. Ciofini, Inorg. Chem., 1999, 38, 1996.
40. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546.
41. T. Müller, M. Dallos, H. Lischka, Z. Dubrovay and P. G. Szalay, Theor. Chem. Acc., 2001, 105, 227.
42. F. Sevin and M. L. McKee, J. Am. Chem. Soc., 2001, 123, 4591.
43. A. G. Leach, K. N. Houk and C. S. Foote, J. Org. Chem., 2008, 73, 8511.
44. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242.
45. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 36, 199.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra19895j

---