A theoretical and experimental study of the crystal structure of H₂V₃O₈

Abstract

The present study aims at clarifying the positions of hydrogen atoms in H₂V₃O₈. Starting with the structure provided by Oka (J. Solid State Chem., 1990, 89, 372) a model was established using first-principles total energy calculations. Optimized structure data were obtained for two possible configurations within the orthorhombic symmetry representation of the V–O frame. The hydrogen atoms were located close to the oxygen atom labelled O(6) by Oka, in a water-like H–O–H moiety. The two different configurations are distinguished by either parallel or perpendicular orientation of the H–O–H plane with regards to the crystallographic b-axis. In addition, neutron diffraction measurements at 4 K and ambient temperature were performed. The hydrogen atom positions were found in proximity of O(6), in a similar arrangement as predicted theoretically. In particular, the structure obtained from the analysis of the 4 K data matches the model with H–O–H plane parallel to the b-axis.

---

1 Introduction

The first reference to H₂V₃O₈ in literature dates back to the late 1960s. By treating hydrated VO₂ in aqueous hydrogen peroxide at 453 K Théobald and Bernard discovered a green product (which they named “phase-F”) with a vanadium average oxidation state between 4.60 and 4.84. In a consecutive publication, they derived an orthorhombic structural model based on the X-ray diffraction (XRD) pattern of the pure so-called F-phase. The chemical composition was established as V₃O₇·H₂O.¹ In 1990, Oka² presented a hydrothermally-synthesized V₃O₇·H₂O as H₂V₃O₈ with orthorhombic Pnma (IT No 62) space group symmetry. The limitations of the X-ray powder diffraction analysis did not make possible the localization of hydrogen atoms. Until today a detailed structural investigation of the positions of hydrogen atoms is missing. Oka² suggested that the oxygen atoms having the longest V–O bond should be those bound to hydrogen atoms. Without any further evidence, the position of hydrogen atoms in the V₃O₈ framework remained an assumption. Therefore, to our best knowledge, the problem of the location of the hydrogen atoms in the V₃O₈ framework is still an open question. Locating protons in a mixed-valence transition metal oxide may also provide further insights into other physico-chemical properties of the material. A distinction between structural water, free protons and/or hydroxyl group is crucial to understand the electronic structure of such a transition metal compound. Hydrogen atoms can be accommodated in transition metal oxides by forming hydrogen metal bronzes with general formula H_xMe_mO_n, where Me stands for the transition metal. For example, in manganese(III–IV) oxide, two types of protons have been characterized, which are referred to as Rütschi and Coleman protons, after the name of their discoverers³ (and reference therein). Rütschi protons refer to substitution protons, which occupy the transition metal sites and Coleman protons are interstitial sites protons. The water moiety and especially the protons play an important role in the stabilization of the structure and influence the electrochemical behavior. In recent years, several groups reported about the electrochemical behavior of H₂V₃O₈ in lithium batteries. H₂V₃O₈ was found to be able to intercalate reversibly more than four equivalents of Li ions and is therefore an interesting candidate as positive electrode material.^4–9 Overall, up to date the published reports focused either on lithium intercalation or on synthesis. In the present work, we aimed to clarify the positions of the hydrogen atoms in the V₃O₈ framework and characterize the nature of the oxygen–proton bonding, by combining crystal structure prediction, via first-principles calculations, and targeted experiments.

2 Methodology

2.1 Synthesis

H₂V₃O₈ was synthesized by using the known hydrothermal method reported by Oka.² Vanadyl sulfate was prepared in-house since commercial products are hydrates of unknown stoichiometry and often contain impurities. In a typical synthesis, 2.2 g V₂O₅ (Alfa Aesar), 0.65 ml H₂SO₄ (97–98% by Sigma Aldrich), 22 ml H₂SO₄ (4–5% by Sigma Aldrich) and 380 ml deionized water were mixed in a 500 ml three-neck (condenser with nitrogen in, nitrogen out and thermometer) round bottom flask equipped with a condenser for reflux. The apparatus was kept under nitrogen during the reaction. The suspension was heated to 353 K. The reaction took two hours to complete. The colour of the reaction mixture changed quickly from orange-yellow to green. Once all vanadium(5+) was reduced to vanadium(4+), a clear deep blue solution of vanadyl sulfate (typically 0.06 M) was obtained. The chemical reaction is known as the contact process:

V₂O₅ + H₂SO₄ + H₂SO₃ ⇀ 2VOSO₄ + 2H₂O (1)

After the hydrothermal step, the as-synthesized green H₂V₃O₈ compound was collected by filtration, rinse twice with deionized water and once with isopropanol. The solid was dried in air stream at room temperature for 3 hours and at 393 K in air overnight. The phase purity and the structure of the product was probed by performing different analyses, SEM, XRD, DTA-TG and TG-MS.

2.2 Spectroscopic measurements

The presence of unpaired electrons of vanadium ions was probed by using a continuous-wave EPR spectrometer operating at X-band (9.5 GHz) (Bruker EMX). The spectra were recorded at 123 K, and the temperature was monitored by a Eurotherm controller.

The ¹H-MAS NMR experiment was performed at an operating frequency of 272.1 MHz, corresponding to a field strength of 16.4 T, on a Bruker Avance ITM 700 MHz Ultrashield. The spectra were acquired using a Bruker double resonance MAS probe head equipped with a 2.5 mm ZrO₂ rotor that was spun at a frequency of 21 kHz. The probe was tuned to ¹H (700.14 MHz) and the spectrum was referenced to distilled water by setting it to 0 ppm.

The IR spectra were recorded on a Brucker FTIR model Vertex 70 and the measurements carried out in air. The resolution was ±4 cm⁻¹.

2.3 Thermal analysis

The DTA was performed with a Netzsch STA 409 in corundum crucibles with heating ramp of 10 K min⁻¹ from room temperature to 973 K. We used nitrogen as carrier gas.

2.4 Neutron diffraction

Neutron diffraction measurements on H₂V₃O₈ were carried out on the high resolution powder diffractometer D2B at the Institute Laue-Langevin, Grenoble and also on the high resolution powder diffractometer SPODI at the FRM II reactor, Garching. The structure refinement was based on the neutron powder diffraction experiments by using the Rietveld method implemented in the program GSAS,¹⁰ part of the EXPGUI package.¹¹ Graphical representations of the structure and the nucleus densities were created with VESTA crystal structure visualization program.¹²

2.5 Computational settings

The set of modelled structures were optimized as the atomic positions and the lattice parameters, without any symmetry constraints, by using the DFT-based code, CASTEP, implemented in Materials Studio 6.0.¹³ We used norm-conserving pseudopotentials and reciprocal space representation for all atoms, and for V and O atoms, the valence shells contain respectively the electrons in the s–p orbitals, the 2s²2p⁴ and 4s²3d³. The Brillouin zone was sampled by using a fine mesh commensurate to the specific lattice dimensions, but with the actual spacing below 0.03 Å⁻¹. The energy threshold, the maximum atomic displacement, the maximum atomic force and the lattice stress were set to 0.005 meV per atom, 0.001 Å, 0.001 eV Å⁻¹ and 0.002 GPa, respectively. We used the generalized gradient form (GGA) of the exchange-correlation functional and in particular the Perdew–Burke–Ernzerhof96 (PBE) one.¹⁴ The dispersion term being one of the important long range contribution to the total energy, non-covalent forces, and in particular van der Waals interactions, were introduced by using damped atom-pairwise dispersion corrections of the form C₆R⁻⁶, proposed by Grimme,^15,16 as implemented in CASTEP.¹⁷

3 Results and discussion

3.1 Experimental results

The stoichiometry V₃O₈ given by Theobald and Oka in their respective works^1,2,18 on V₃O₈ was also confirmed by our diffraction experiments. Nevertheless, the hydrogen stoichiometry could deviate from 2. V₃O₈ is known to be an intercalation compound and therefore the structure may be stable for the hydrogen content in the range 2 ± δ. For this reason, we review some of the experimental results obtained by techniques detecting either hydrogen or unpaired electrons in H₂V₃O₈. Electron paramagnetic resonance spectroscopy (EPR) was used to probe unpaired electrons. Since H₂V₃O₈ is green, vanadium is expected to be found in the two oxidation states: 4+ and 5+. Each vanadium(IV) ion contains one unpaired (3d¹) electron which strongly interacts through exchange forces with the surrounding atoms. The EPR signal originating from the unpaired electron, d¹ in V⁴⁺, is shown in Fig. 1.

Fig. 1 The EPR spectrum of the as-synthesized H₂V₃O₈.

In a second spectroscopic investigation, ¹H-MAS-NMR was used to probe the protons in pristine H₂V₃O₈. The spectrum in Fig. 2 displays one signal at 41 ppm with asymmetric spinning sidebands, i.e. all protons were found magnetically equivalent within the chosen experimental parameters. The spinning sideband pattern reflects the anisotropy of the coupling interaction between the protons and the paramagnetic centers, which can be described by the appropriate tensor. The small peaks around 5 ppm are due to background subtraction.

Fig. 2 Experimental NMR spectrum of H₂V₃O₈.

Using the combined information delivered by EPR and H-NMR, we can state that H₂V₃O₈ contains protons and unpaired electrons. At this point, the composition H_2±δV₃O₈ is confirmed, although no quantification of the protons and unpaired electrons can be made based on that information alone. The IR spectra were recorded in order to gain more information about the nature of hydrogen–oxygen bonding. The experimental IR spectrum in Fig. 3 showed four main bands, in agreement with the literature.^7,19–21 They are: the bridging oxygen–vanadium–oxygen bond at around 780 cm⁻¹; the stretching of vanadium(IV)–oxygen bond and vanadium(V)–oxygen bonds at 969 cm⁻¹ and 1009 cm⁻¹, respectively; and the bending vibration of water at 1658 cm⁻¹. The broad and very low intense peak in the range of 3500 cm⁻¹ can be attributed to the O–H stretching modes. Their intensity is reduced because of the constrained environment of the O–H moieties. For comparison, in the vibrational spectra of liquid water, the bending mode, ν₂, is reported in the range of 1632–1643 cm⁻¹, while for example, the bending mode of water molecules in zeolites²² falls in the range 1500–1700 cm⁻¹. The presence of the bending vibration of water-like moiety indicates that at least some of the protons are bound to oxygen as in molecular water and confirms the presence of H–O–H configuration.

Fig. 3 Experimental IR spectrum of H₂V₃O₈.

The TG-DTA measurements were conducted in order to get quantitative information on the exact content of hydrogen. The thermal gravimetric measurements of the as-synthesized H₂V₃O₈, qualitatively in agreement with the literature data,^{7,8,19–21,23,24} showed the weight loss of 6.31%, which corresponds to one equivalent of molecular water per formula unit. A molecular ion with m/z = 18 was, in fact, detected in a TG-MS measurement.²⁵ The thermogravimetric analysis as a function of the temperature is shown in Fig. 4. In particular, the DTA curve in Fig. 4 shows an endothermic peak related to a completed water loss at 620 K, immediately followed by an exothermic peak at 695 K. For temperature above no further weight loss was observed, indicating that the thermal decomposition is complete and that any subsequent process does not change the chemical composition but may involve a phase change. In fact, the exothermic process, which has been recently reported²¹ to occur at 650 K, was attributed by the authors to the formation of V₃O₇ phase. The molecular water is a structural building unit in H₂V₃O₈, whose orthorhombic lattice collapses upon H₂O removal and recrystallizes about 690 K in one or multi-component vanadium oxide phases (see the ESI for details†). Although H₂V₃O₈ may occur as a proton-deficient or a proton-rich compound, our results agree with the stoichiometry H₂V₃O₈ so far reported in literature.

Fig. 4 The TG- and DTA-curves of the as-synthesized H₂V₃O₈.

Two neutron powder diffraction experiments, one at ambient temperature and one at 4 K are compared in Fig. 5.

Fig. 5 Rietveld refinements of H₂V₃O₈ based on neutron diffraction data obtained at ambient temperature (a) and 4 K (b). The observed (red), calculated (green) and difference (purple) patterns are shown, reflection positions are marked in black.

The starting model structure was that provided by Oka.² Since the bound coherent neutron scattering length for vanadium is very small (−0.3824(12) fm) compared to the ones of oxygen (5.803(4) fm) and hydrogen (−3.7390(11) fm), the positions of the vanadium atoms were taken from a Rietveld refinement based on synchrotron powder diffraction data of a partially deuterated sample and excluded from the subsequent refinements. To further reduce the number of free parameters, the displacement parameters of all atoms were constrained to be equal. For the ambient temperature data, the hydrogen atom positions H(1) and H(2) in Fig. 6 were located in the difference Fourier map and their positional parameters were refined freely, whereas the occupancy factors were set to 0.5 each. A free refinement of the occupancy factors of the disordered positions converges at a total occupancy of about 2/3 with almost equal distribution on both sites, which corresponds to a sum formula of H_1.3V₃O₈. However, it is obvious that the smeared nucleus density resulting from the disorder cannot be described properly by simple isotropic displacement parameters of the hydrogen atoms. Therefore, in principle, it might be possible that the missing 1/3 of a hydrogen atom is contained in the residual nucleus density, not covered by the displacement parameters of H(1) and H(2), as shown in Fig. 6, panel (a).

Fig. 6 (a and b) The coordination spheres of V(2) and the partially occupied hydrogen atom positions H(1) and H(2) bonded to O(6), shown together with the isosurfaces of the nucleus density (−0.78 fm in blue and 0.78 fm in yellow). (c and d) Observed Fourier map of a mean plane through the partially occupied hydrogen atom positions. H(1), H(2) and their symmetry equivalent positions, isovalues in steps of 0.2 fm from −3.74 to 3.74, blue for negative, H(1) and H(2), and red for positive, O(6), values, respectively. Results of (a) and (b) are derived from data obtained at ambient temperature and 4 K, respectively. The V(2)–O(6) bond length is larger (2.346 Å, in the structure 1 and 2.371 Å in the structure 2) that the other five V–O bonds, for that it is not considered in the coordination of V(2) atoms. A 3-D view of the modelled structures: structure 2 (e) and structure 1 (f). In (e) the two non-equivalent H atoms are coloured differently (light blue and white, which in the highlighted V–O group becomes light blue and dark blue) and in (f) the equivalent H atoms are coloured in white (which turn in blue in the highlighted V–O group). The V atoms are in grey and the O atoms in red, which in the highlighted V–O group becomes dark-green and brown, respectively.

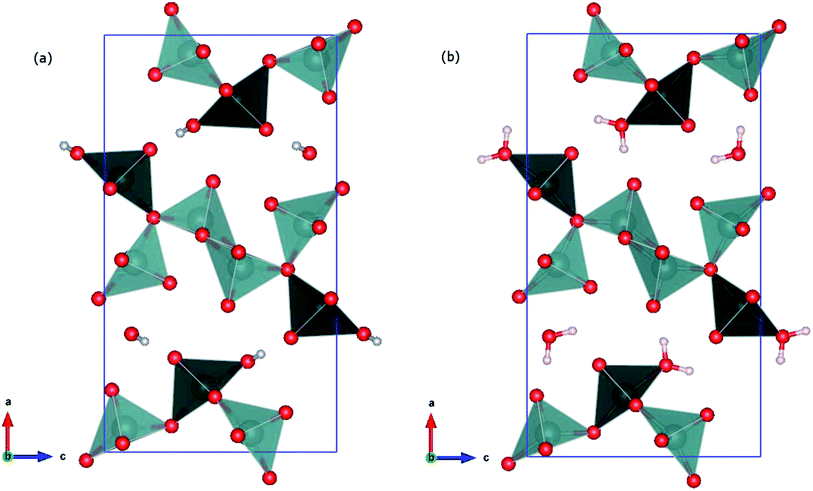
For the 4 K data, only one hydrogen atom position was found close to O(6) corresponding to the H(2) position of the ambient temperature data, and refined with free positional parameters. A refinement of the occupancy factor converges at about 0.6, very similar to the value found at ambient temperature. It is remarkable, that in both refinements, the total occupancy of the hydrogen atoms converge only at around 0.6, instead close to a full occupancy, as it would be the case for a water molecule. However, it has to be emphasized, that the resolution of the neutron diffraction pattern does not allow unambiguously to prove a partial occupancy of the hydrogen atom positions. Therefore the occupancies for both, ambient temperature and 4 K, were set to 1 for the final refinement. Crystallographic data and structure refinement at room temperature and 4 K are provided in Table 1. It seems that the disorder of H(1) and H(2) observed for ambient temperature data is dynamic and the two non-symmetry equivalent positions merge to just one symmetry-equivalent hydrogen position at 4 K, shown in Fig. 6, panel (c). No further significant residual nucleus density was identified (largest residual peaks with about ±0.1 fm). In Fig. 6, panels (e) and (d) the two model structures found via first-principles modelling are reported. They are described in the following section.

Table 1 Crystallographic data and structure refinement of H₂V₃O₈

a The standard uncertainties determined from powder data are based on counting statistics only and neglect all systematic errors. In fact, more realistic Rp values are about ten times larger.
Empirical formula	H2V3O8	H2V3O8
Temperature	293(2) K	4 K
Crystal system	Orthorhombic	Orthorhombic
Space group	Pnma – D^162h	Pnma – D^162h
Unit cell dimensions^a	a = 16.8593(7) Å	a = 16.7510(6) Å
	b = 3.63401(13) Å	b = 3.64051(10) Å
	c = 9.3260(4) Å	c = 9.25217(29) Å
Volume, Z	571.37(4) Å^3, 4	4564.219(31) Å^3, 4
Density	3.280 g cm^−3	3.321 g cm^−3
Measurement	Neutron beamline D2B	Beamline SPODI
	Institute Laue-Langevin,	Forschungs-Neutronenquelle
	Grenoble, France	Hans-Maier-Leibnitz (FRM II)
		TU München
Wavelength	λ = 1.594 Å	λ = 1.54815(2) Å
No. variables	36	33
Final R values	wRp = 0.0181	wRp = 0.0238
	Rp = 0.0137	Rp = 0.0179
	χ^2 = 2.663	χ^2 = 10.52
	R(F^2) = 0.0804	R(F^2) = 0.1174

---

3.2 Theoretical localization of hydrogen atoms

From the structural modelling standpoint, the crystal structure problem can be handled in two ways. One could consider the structure of vanadium heptaoxide and add in the stoichiometric amount of H₂O to form H₂V₃O₈. Alternatively, one can start from the molecular skeleton of V₃O₈ (ref. 2) and add two hydrogen atoms per formula unit. H₂V₃O₈ and V₃O₇·H₂O are reported in the literature indicating the same compound because of a lack of knowledge about the exact location of the hydrogen atoms. Clearly, the orthorhombic lattice of H₂V₃O₈ cannot be derived from the reaction V₃O₇ + H₂O. As a consequence, the formulation H₂V₃O₈ and the position of vanadium and oxygen atoms, suggested by Oka² appears to us as the convenient piece of information to start with. In the following we report the results obtained by using the V₃O₈ framework as the starting model structure. From the structural modelling standpoint, the problem of the localization of the hydrogen atoms in V₃O₈ framework can be reduced to a search for symmetry-allowed sites, which occupancy preserve the orthorhombic symmetry representation of the lattice. Monte Carlo calculations, and in particular bias Monte Carlo method implemented in Materials Studio 6.0, provided the most likely sites where hydrogen atoms can reside. This was done by sequential addition of hydrogen atoms to the host lattice formed by the V₃O₈ network. A canonical Monte Carlo sampling through a number of temperature cycles of the simulated annealing algorithm was used for that purpose. The lowest energy sites for the hydrogen atoms in the framework of V₃O₈ were identified by repeatedly searching the configurational space of the V₃O₈–H system. Fig. 7 shows a top-view of the V₃O₈ framework with hydrogen atom locations suggested by Monte Carlo simulations.

Fig. 7 A top-view along the b-direction of the double cell of H₂V₃O₈, in which the hydrogen atoms are localized with their motion sphere as suggested by the Monte Carlo simulations. The radius of the motion spheres is for visualization purpose. Representing colours: vanadium, gray; oxygen, red; hydrogen, white.

By symmetry the general site (x, 0.25, z) in the orthorhombic lattice, with x, z chosen to be close to the [V⁴⁺O] moiety, can be occupied by hydrogen atoms up to reach the stoichiometry of H₂V₃O₈. That means two sets of sites (x₁, 0.25, z₁) and (x₂, 0.25, z₂). In addition, the general position (x, 0.5, z) has multiplicity of two with the hydrogen atoms lying along the b-direction. The optimized structure data of the two possible configurations with the orthorhombic symmetry representation of the V–O frame, are reported in Table 2.

Table 2 Theoretically optimized atomic positions of the two structures of H₂V₃O₈, symmetry space group Pnma (No 62), at DFT-D level. The structure 1 exhibits the hydrogen atoms along the b-direction. In structure 2 the hydrogen atoms are situated on the (0 4 0) plane. The two structures differ by 17.75 kJ mol⁻¹, with the first lower in energy. The average (avg) values of the lattice parameters of the two structures are closer to the experimental lattice parameters and the ones reported by Oka:² a_avg = 16.974 Å, b_avg = 3.612 Å, c_avg = 9.396 Å

Species	x	y	z	Site
a a = 16.6597 Å, b = 3.6313 Å, c = 9.2647 Å. Vc = 560.4807 Å^3, Z = 4.b a = 17.2885 Å, b = 3.5919 Å, c = 9.5270 Å, Vc = 591.613 Å^3, Z = 4.
Structure 1^a
H(1)	0.2652	0.5350	0.1735	8d
V(1)	0.4550	1/4	0.1287	4c
V(2)	0.1543	1/4	0.4286	4c
V(3)	0.0562	1/4	0.0873	4c
O(1)	0.0391	1/4	0.5741	4c
O(2)	0.4054	1/4	0.2810	4c
O(3)	0.8676	1/4	0.5246	4c
O(4)	0.0623	1/4	0.2885	4c
O(5)	0.2256	1/4	0.3036	4c
O(6)	0.2168	1/4	0.6169	4c
O(7)	0.4796	1/4	0.5782	4c
O(8)	0.1485	1/4	0.0319	4c
Structure 2^b
H(1)	0.2719	1/4	0.5855	4c
H(2)	0.2026	1/4	0.6941	4c
V(1)	0.4541	1/4	0.1279	4c
V(2)	0.1442	1/4	0.4187	4c
V(3)	0.0530	1/4	0.0887	4c
O(1)	0.0379	1/4	0.5760	4c
O(2)	0.4013	1/4	0.2710	4c
O(3)	0.8781	1/4	0.5338	4c
O(4)	0.0572	1/4	0.2857	4c
O(5)	0.2168	1/4	0.3097	4c
O(6)	0.2160	1/4	0.5953	4c
O(7)	0.4829	1/4	0.5797	4c
O(8)	0.1437	1/4	0.0409	4c

---

A 3D view of the optimized structures is reported in Fig. 8. The polyhedra show the coordination of vanadium atoms. The V–O bonds are cut through up to a distance of 2.35 Å.

Fig. 8 A top-view of the unit cell of the orthorhombic structure of H₂V₃O₈. The location of hydrogen atoms are (a) perpendicular to b-direction in the structure 1 and (b) in-plane, ac-plane, in structure 2. Representing colours: hydrogen, white; vanadium, green; oxygen, red.

The two structures differ by 17.75 kJ mol⁻¹ being lower in energy the one with the hydrogen atoms aligned along the b-direction (structure 1). The two possible locations of hydrogen atoms can be thought as two possible states easily accessible by thermal activation from one state to the other. In addition, the energy difference between the two structures is of the same order of the free rotational energy of molecular H₂O. Therefore, the vibrational and rotational modes are sufficient to mimic a sort of de-localized proton between two adjacent V₃O₈ units. Interestingly, in the higher energy structure (structure 2) there are two non-equivalent hydrogen atoms by symmetry, while in the lowest energy structure all hydrogen atoms are equivalent. Our NMR calculations confirmed that in the lowest energy structure all protons have the same chemical shift, while in the higher energy structure the two hydrogen atoms are not magnetically equivalent, which is reflected into the different values of the corresponding chemical shifts. Therefore, the lattice parameters of the room-temperature structure can be considered as the mean values of the corresponding lattice parameters of the two structures found computationally. A comparison of the low temperature (4 K) neutron diffraction pattern with the simulated patterns of the two predicted positions of hydrogen atoms in H₂V₃O₈, orthorhombic symmetry space group, is reported in Fig. 9. The two alignments of the hydrogen atoms in the V₃O₈ framework induce a relative shift of the diffraction peaks of the planes (2 0 0) and (1 0 1), which are the planes mainly affected by the O–H interactions between H–O–H moieties. Differences in the diffraction peaks mirror the dynamics of the hydrogen atoms into the lattice. Deviations from the experimental patterns indirectly highlight a sort of (de)localization of hydrogen atoms, which might be not correctly accounted in the particular functionals (exchange-correlation and dispersion contribution) used. Clearly, the exact identification of the sites most visited by the hydrogen atoms in the lattice is an important piece of information, because their localization affects the lattice parameters, the length of the V–O bonds and the oxidation state of V atoms.

Fig. 9 (a) The simulated neutron diffraction pattern of the lowest energy structure of H₂V₃O₈ is overlapped with the experimental neutron data at T = 4 K. (b) A detailed view in the region 10–11 degrees of 2θ shows the relative shift of the diffraction peak of the (1 0 1) plane due to the lattice relaxation and the dynamics of hydrogen atoms into the lattice.

4 Conclusions

In our DFT-optimized crystal structure model of H₂V₃O₈, the hydrogen atoms reside close to the O(6) oxygen atoms in two possible configurations differing by 17.75 kJ mol⁻¹, with H–O–H plane either perpendicular or parallel to the crystallographic b-axis. The two possible locations of hydrogen atoms can be thought of as two possible states easily accessible by thermal activation. Neutron diffraction were performed at room temperature and 4 K. For the ambient temperature data, two non-equivalent hydrogen atom positions have been found. For the 4 K data, only one hydrogen atom position was found close to O(6) corresponding to the H(2) position of the ambient temperature data. It is remarkable, that in both refinements, the total occupancy of the hydrogen atoms converged only at around 0.6, instead to a full occupancy, 1.0, as it would be the case for a water molecule. On the other side, it has to be emphasized that the refinement of the neutron diffraction data does not allow to prove unambiguously the site occupancy by hydrogen atoms. The chemical nature of the structural H₂O moiety in H₂V₃O₈ is definitely more complex than that of simply crystal-trapped molecular water. Water cannot be removed from H₂V₃O₈ without destroying the original structure and even if the V(2)–O(6) distance is longer than the typical V–O single bond distance in vanadates, the O(6) resides in the first coordination shell of vanadium. Furthermore, the combination of the long-range hydrogen bond interactions between H–O–H moieties and the thermally-activated motion of the O–H bonds may cause randomness of the H atoms in the room-temperature structure and consequently induce changes in the oxidation state of vanadium atoms in close proximity to the oxygen of H–O–H moiety. This ought to be a typical problem of the (de)localization and dynamics of hydrogen atoms in transition metal oxides.

Acknowledgements

The authors thank Christian Mensing, Michael Wörle, Santhosh Matam, Reinhard Kissner and René Verel for the DFT-TG, XRD, IR, EPR and NMR measurements. Special thank to Michael Wörle for the analysis of the neutron diffraction data and to Reinhard Nesper for his valuable comments. The computer facilities at ETH, Zürich are highly appreciated. The authors acknowledge supports of the neutron scattering centers of Institut Laue-Langevin, Grenoble and MLZ, FRM II. and thank E. Suard and A. Senyshyn for their helps in neutron diffraction data collection.

References

1. F. Theobald and J. Bernard, C. R. Seances Acad. Sci., Ser. C, 1970, 270, 2138.
2. Y. Oka, T. Yao and N. Yamamoto, J. Solid State Chem., 1990, 89, 372.
3. C. Pitteloud, M. Nagao, K. Itoh and R. Kanno, J. Solid State Chem., 2008, 181, 467.
4. K. Waltersson, B. Forslund, K. Wilhelmi, S. Andersson and J. Galy, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 2644.
5. G.-C. Li, S.-P. Pang, Z.-B. Wang, H.-R. Peng and Z. Zhi-kun, Eur. J. Inorg. Chem., 2005, 11, 2060.
6. S.-I. Mho, C. Reddy and Y. Kim, J. Korean Phys. Soc., 2009, 54, 2420.
7. V. L. Volkov and G. S. Zakharova, Russ. J. Inorg. Chem., 2009, 54, 1704.
8. G. S. Zakharova, V. L. Volkov, C. Taeschner, I. Hellmann, A. Leonhardt, R. Klingeler and B. Buechner, Solid State Commun., 2009, 149, 814.
9. J. Prado-Gonjal, B. Molero-Sánchez, D. Ávila-Brande, E. Morán, J. Pérez-Flores, A. Kuhn and F. Gárcia-Alvarado, J. Power Sources, 2013, 232, 173.
10. A. Larson and R. von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory, Report LAUR 86–748, 1994.
11. B. Toby, J. Appl. Crystallogr., 2001, 34, 210.
12. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272.
13. S. Clark, M. Segall, C. Pickard, P. Haspin, M. Probert, K. Refson and M. Payne, Z. Kristallogr., 2005, 220, 567.
14. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
15. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
16. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
17. E. R. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414.
18. F. Theobald and J. Bernard, C. R. Seances Acad. Sci., Ser. C, 1969, 268, 60.
19. H. Li, T. Zhai, P. He, Y. Wang, E. Hosonoa and H. Zhou, J. Mater. Chem., 2011, 21, 1780.
20. V. Channu Reddy, R. Holze and B. Rambabu, Curr. Appl. Phys., 2013, 13, 237.
21. Q. An, J. Sheng, X. Xu, Q. Wei, Y. Zhu, C. Han, C. Niu and L. Mai, New J. Chem., 2014, 38, 2075.
22. C. Geiger, Eur. J. Mineral., 2012, 24, 439.
23. S. Gao, Z. Chena, M. Wei, K. Wei and H. Zhou, Electrochim. Acta, 2009, 54, 1115.
24. Y. Zhang, M. Zhou, M. Fan, C. Huang, C. Chen, Y. Cao, H. Li and X. Liu, Curr. Appl. Phys., 2011, 11, 1159.
25. Y. Mettan, PhD thesis, ETH Zürich, Diss. Nr 19382, 2011.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra19665e

---