A catalytic route to dibenzodiazepines involving Buchwald–Hartwig coupling: reaction scope and mechanistic consideration

Abstract

We report a new synthetic method for the synthesis of a family of dibenzodiazepines (DBDAs), employing Pd-catalyzed C–N coupling of o-bromoaldimine, with o-bromoaniline as the key step. Eleven DBDAs were prepared, containing electron-withdrawing groups (CN, F, NO₂) and electron-donating groups (OMe). The reaction conditions were optimized (catalyst, phosphine, base and solvent) and best results were obtained with Pd(OAc)₂, SPhos, Cs₂CO₃ in THF. Due to the ambiguity of the mechanism at hand, various mechanistic studies were performed, that included DFT calculations. The oxidative addition process was studied in detail by DFT, and these studies supported the observed reaction regioselectivity. The adducts formed between the aldimine and the Pd(0) catalyst were calculated to be more stable than the ones formed with the amine, and the barrier for the oxidative addition at the C–Br bond of the aldimine was calculated to be lower than the one at the C–Br bond of the aryl amine. The formation of DBDA over the dibenzoaminopiperidine has been explained in the final cyclization step.

---

Introduction

Chemists have long been interested in tricyclic heteroaromatic compounds due to their biological activity.¹ Nitrogen-containing compounds such as azepines and 1,4-diazepines are recurring structural units of pharmaceutical importance.^2,3 Benzodiazepines are indeed a ubiquitous class of pharmaceutical drugs used to treat a variety of mental diseases. For example, alprazolam (Fig. 1) is a benzodiazepine used to treat psychotic disorders.⁴ It is a potent antipsychotic drug, whose action consists of binding to GABA A receptors. Dibenzodiazepines (DBDA) are a sub-class of these pharmaceuticals, and consist of a diazepine fused with two benzene rings. Clozapine (8-chloro-11-(4-methylpiperazino)-5H-dibenzo[b,e][1,4]-diazepine),⁵ (Fig. 1), is probably the most famous dibenzodiazepine due to its presence on the World Health Organization model list of essential medicines.⁶ It contains a dibenzooxazepine unit. Despite its side effects,⁷ clozapine is the molecule of choice for treating schizophrenia.⁸ In dopamine related mental illnesses, the D2 dopamine receptor is typically targeted.^9–11 Several clozapine derivatives are now known. Hydrazides of clozapine have been synthesized,^12,13 and clozapine analogues such as HX531 were recently reported.¹⁴ They were found to be efficient Retinoid X Receptors (RXR) antagonists, which make them potential interesting drugs for treating diseases such as diabetes or obesity. It was found that the antagonistic activity heavily depends on the substituents present on the fused phenyl rings.¹⁵ A synthesis of iozapine, whose structure is the same as clozapine, except that an iodine atom replaces the chlorine on the fused ring, has been described.¹⁶ Dibenzepine (Fig. 1) is another dibenzodiazepine used to treat depression.¹⁷ Small modifications of the dibenzodiazepine scaffold can thus have big impacts on their biological activity,^18,19 justifying the importance of increasing the availability of such compounds. Various successful pharmaceutical compounds consist of similar backbones. The thienobenzodiazepine olanzapine, which is used, among others, to treat bipolar disorders, and the atypical antipsychotic quetiapine (a dibenzothiazepine) are notable examples.^20,21

Fig. 1 Drugs containing the diazepine scaffold, and our original target family.

Synthetic strategies for simple benzoazepines are now widely available.^22,23 Nevertheless, there are still few synthetic methods available for the DBDA backbone (or for related compounds),²⁴ and most employ the Bischler–Napieralski reaction which consists of an intramolecular electrophilic aromatic substitution.^25–29 Corrosive POCl₃ is typically needed to afford the cyclization, and the reaction usually starts with arylamides or arylcarbamates. Pyridothiobenzazepines were thus synthesized this way.^25,26 A Friedel–Crafts cyclisation (also using POCl₃) was reported, using an NO₂ group.²⁹ Several strategies consist of reduction of a nitro group to an amine, followed by formation of a lactam intermediate (like for the synthesis of iozapine).^16,30 An intramolecular amination process affording dibenzodiazepinones and pyridobenzodiazepinone was recently published, using 2-nitrobenzoyl chloride and an amine.³¹ A palladium-catalyzed condensation using aniline derivatives was used by Buchwald to afford various dibenzazepines.³² They later reported a similar method allowing the synthesis of various DBDAs, and dibenzooxazepines as well. All the reported DBDAs are substituted at the carbon end of the imine.³³ They avoid the use of a NO₂ group by substituting the benzene ring with two halides, one of them a chlorine, taking advantage of the higher reactivity of the C–Br bond towards Pd. An interesting transition-metal free synthesis of DBDA was recently reported.³⁴ Despite these recent advances, new procedures for accessing the DBDA backbone, and particularly the dibenzooxazepine core are still needed. Herein, we report the first palladium catalyzed synthesis of dibenzodiazepines using o-bromoarylamines and o-bromoarylimines, under Buchwald–Hartwig amination^35–37 conditions (Scheme 1). In this method the use of 1,2-dihalobenzenes is avoided. Contrary to the synthesis reported in ref. 33, the synthesis is performed in a one-pot fashion.

Scheme 1 Optimized conditions for the synthesis of DBDA-4.

Results and discussion

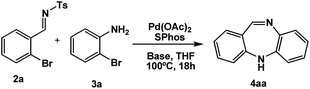
Due to our group's interest in the catalytic arylation of aldimine substrates,^38–40 we initiated a program to access the feasibility of reacting electron deficient aldimines with o-haloanilines in the presence of a Pd catalyst in an effort to carry out a sequential Buchwald–Hartwig/imine arylation process to give tricylic chiral dibenzoaminopiperidines (or hydrogenated acridines) (Fig. 1), that can act as chiral tacrine analogues for acetylcholine esterase inhibition. To our surprise, when aldimine (2a) was treated with bromoaniline (3a) in the presence of Pd(OAc)₂/SPhos^41,42 and Cs₂CO₃ as base, it unexpectedly gave DBDA (4aa) in 70% yield (Table 1, entry 1).

Table 1 Pd-catalyzed synthesis of DBDA (4aa); solvent and aldimine (2a–c) screening^a

Entry	Aldimine (2)	Solvent	Yield^b/%
a Reaction conditions: aldimine (2) (1 mmol), bromoaniline (3) (1 equiv.), Pd(OAc)2 (2.5 mol%), SPhos (5 mol%), Cs2CO3 (2 equiv.) and solvent (3 mL), stirring at 100 °C.b Isolated product after liquid column chromatography with SiO2 gel. Ts = tosylate, Ms = mesylate, Ns = nosylate.
1	(2a)	THF	70
2		Toluene	60
3		1,4-Dioxane	46
4		DME	23
5		DMF	57
6		CH3CN	28
7		DCM	30
8	(2b)	THF	85
9		Toluene	41
10		1,4-Dioxane	54
11		DME	34
12	(2c)	THF	30
13		Toluene	40
14		1,4-Dioxane	45

---

This interesting result encouraged us to screen several reaction conditions in order to optimize the method and to conduct theoretical calculations in order to understand the mechanism. The aldimines (2a–c), were synthesized, (Scheme 1) by condensing benzaldehyde (1) with three different amines. Three aldimines (2a–c) with different protecting groups were screened, using the same catalytic system as before. We screened a variety of solvents and the results are collected in Table 1. In general, the reaction works with moderate yields in non-polar solvents like toluene or moderately polar solvents like 1,4-dioxane, regardless of the protecting group present in the aldimine substrate (2) (Table 1, entries 2, 3, 9, 10, 13 and 14). But when THF was used, better yields of (3a) were obtained for aldimines (2a) and (2b) (Table 1, entries 1 and 8, respectively). With dichloromethane (DCM), dimethylformamide (DMF) or dimethoxyethane (DME) the yields were lower (Table 1, see for instance entries 7, 5 and 4). Better yields were obtained using THF in the case of PG = Ts and Ms (70 and 85%, respectively), and 1,4-dioxane in case PG = Ns (45%) (see Table 1, entries 1, 8 and 14).

The best overall yields in the synthesis of the DBDA, starting from o-bromobenzaldehyde are shown in Scheme 1 (the best yield was obtained with 2a, PG = Ts, 64.4%).

The contributions over the years from the research groups of Buchwald and Hartwig with regard to C–N coupling with aryl halides and anilines in the presence of a suitable phosphane ligand and palladium catalysts have been immense.^35–37,42 In our case we have set-about optimizing our conditions by screening the key ingredients such as the bases (Table 2), the ligand and the palladium catalyst (Table 3).

Table 2 Bases screened for the synthesis of DBDA (4aa)^a

Entry	Base	Yield^b/%
a Reaction conditions: aldimine (2a) (1 mmol), bromoaniline (3a) (1 equiv.), Pd(OAc)2 (2.5 mol%), SPhos (5 mol%), base (2 equiv.) and THF (3 mL), stirring at 100 °C.b Isolated product after liquid column chromatography with SiO2 gel.
1	Cs2CO3	70
2	K2CO3	68
3	Na2CO3	66
4	CaCO3	40
5	Ba(OH)2	20
6	KOAc	30
7	NEt3	12
8	DIPA	4
9	NMM	6
10	DBU	18

---

Table 3 Phosphane ligands screened for the synthesis of DBDA (4aa)^a

Entry	Ligand	Yields^b (%)
		Pd(OAc)2	Pd2(dba)3
a Reaction conditions: aldimine (2a) (1 mmol), bromoaniline (3a) (1 equiv.), Pd(OAc)2 or Pd2(dba)3 (2.5 mol%), stirring at 100 °C.b Isolated product after liquid column chromatography with SiO2 gel.c Catalyst (7.5 mol%), ligand (5 mol%), Cs2CO3 (2 equiv.) and THF (3 mL), stirring at 100 °C.
1	PPh3	40	41
2	CyJohnPhos	51	51
3	SPhos	70	48
4	RuPhos	42	36
5	PCy3	54	47
6	P(n-Bu)3	30	12
7	P(t-Bu)3	62	68

---

	Catalyst^c
8	PEPPSI-iPr	42
9	PdCl2(dppf)	19
10	Pd(PPh3)4	23

---

According to the results presented in Table 2, we conclude that inorganic bases, mostly carbonated ones, afforded the desired DBDA compound (4aa) in moderate to good yields (Table 2, entries 1 to 4). The reaction fails to occur, or gives poor yields of (4aa) using hydroxides (Table 2, entry 5). Organic bases like NEt₃, DBU, NMM, or DIPA gave poor yields (<20%) (Table 2, entries 7–10). It has been reported that Pd-catalysts in conjunction with Cs₂CO₃ facilitate large functional group compatibility (contrary to traditional MOtBu or MOH, M = Group 1 metal).^43,44 In our system, palladium complexes in conjunction with (o-biphenyl)PCy₂ gave good results when M₂CO₃ type bases were used (Table 2, entries 1 to 3). We thus selected Cs₂CO₃ as the base of choice for this transformation.

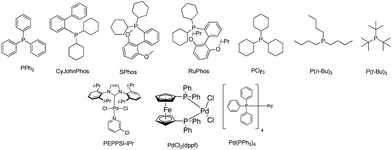
In order to finely tune the catalytic activity,^45,46 we also screened the ligands and catalysts. Several commercial phosphane ligands and Pd-complexes were tested (Table 3). According to the literature,^41,42a dialkylbiaryl phosphane ligands^42b allow this type of reaction to proceed with short reaction times, with lower catalyst loadings and mild conditions. Several authors have looked at various combinations of palladium and phosphane ligands for the Buchwald–Hartwig reaction, like for example: Pd(OAc)₂ or Pd(dba)₂/P(t-Bu)₃ ^42c/PCy₃; PPh₃,^42d but also complexes of the type PdCl₂(dppf),^42e Pd(PPh₃)₄ ^42f and NHC–Pd (PEPPSI). In our case the best yield of 70% was obtained using Pd(OAc)₂/SPhos (Table 3, entry 3) but a close 68% yield was obtained with Pd₂(dba)₃/P(t-Bu)₃ (Table 3, entry 7). Low yields were obtained with P(n-Bu)₃ (Table 3, entry 6), this may be due to the bulky or floppy nature of the phosphane butyl chains causing significant stereo-hindrance within the coordination sphere of the metal. The presence of the i-Pr groups in Ruphos might explain the lower yields (Table 3, entry 4) compared with those for Sphos (Table 3, entry 3) and CyJohnPhos (Table 3 entry 2). In the case of the Pd complexes (Table 3, entries 8, 9 and 10), the PEPPSI catalyst presents the better yield (42%). In the case of PPh₃ (Table 3, entries 1 and 10) we can see that yields are identical for both Pd(OAc)₂ and Pd₂(dba)₃ (about 40%) but decrease when Pd(PPh₃)₄ is used (23%).

We then conducted a study to access the reaction scope. We screened several aldimine (2) and bromoaniline (3) derivatives, using our optimized conditions (Scheme 2). A fine cross-section of both electron rich and electron poor aldimines and bromoanilines were screened. No specific trends were observed, except that the presence of strong electron-withdrawing groups (like, CF₃, NO₂ and CN) in the aniline unit gave lower yields, 46 and 60% yields (Scheme 2, (4ab), (4ad) and (4ae)). The position of the substituent in the ring doesn't appear to influence the yield (see (4ea) vs. (4fa) in Scheme 2).

Scheme 2 Pd-catalysed synthesis of DBDA analogues (4).

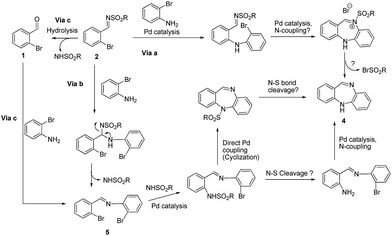
Establishing the mechanism of the reaction was our next concern. We assumed from the outset that the Buchwald–Hartwig reaction would be the first in the sequence, followed by cyclization on the imine nitrogen, and then subsequent N–S bond cleavage, perhaps, by attack on the sulfonamide group by the bromide (Via a, Scheme 3). In the second mechanistic postulate (Via b, Scheme 3), we propose first a trans-imination reaction to give the dibromo-imine, via direct addition of the bromo-aniline on the activated imine,^47–49 followed by sulfonamide elimination. This could be catalyzed by Pd or not. This might be followed by a Buchwald–Hartwig reaction with the sulfonamide (according to literature precedence⁵⁰) to give the o-sulfonylamino-imine, which can conceivably lose the arylsulfonate unit prior to a second Buchwald–Hartwig reaction to give the benzodiazepine (4) (Scheme 3) or undergo the Buchwald–Hartwig reaction followed by arylsulfonate cleavage to give product (4). In either case, the regioselectivity of the Buchwald–Hartwig reaction is indifferent, as it will give the same cyclized products. Theoretically this might also occur via the aldehyde substrate 1 that could be formed via hydrolysis of imine (2), the o-bromoaniline could react with the aldehyde to form the imine (5) (Via c) and on going through mechanistic pathway b would give product (4), via either of the two routes shown in the Scheme 4. We then embarked on studies to probe the reaction mechanism. We could immediately eliminate the possibility of the reaction occurring via Vias b and c, when we subjected imine compound (5), prepared independently, to the same reaction conditions, only starting material and NH₂Ts were recovered (pathway a, Scheme 4). Although Via c would seem unlikely, as there is very little possibility of hydrolysis occurring in the reaction due to the anhydrous conditions that are employed, we conducted the experiment as shown in Scheme 4, that involved using o-bromobenzaldehyde with o-bromoaniline, under the same reaction conditions and we obtained our target compound (4) in 39% yield. This is in fact another approach to accessing benzodiazepine skeletons (which we are currently actively pursuing). On the basis of our subsequent studies (vide infra) presumably imination occurs first to give the imine (2) (Scheme 3) that then undergoes the Buchwald–Hartwig coupling reaction with o-bromoaniline to give product (4) after cyclization during the reaction (that is suggested to occur in Via b). We also independently synthesized imine (5) (Scheme 4), and on subjecting this to the same reaction conditions failed to give (4), giving just starting material and NH₂Ts. The fact, that this second reaction failed to work, disproves the possibility of the reaction occurring through Via b (Scheme 3) making it most likely that the reaction takes place through Via a (Scheme 3). The mechanism for the formation of (4) through pathway b (Scheme 4), and not shown in Scheme 3, is presented in Scheme 4 (inset). We expect that there would be a Buchwald–Hartwig coupling reaction to give the o-N-tosylaminobenzaldehyde intermediate followed by a second Buchwald–Hartwig coupling to form the N-(o-benzoyl)aminoaniline intermediate which could then condense intramolecularly to give (4). The actual phase of the N–S cleavage reaction remains to be seen.

Scheme 3 Possible reaction mechanisms to afford compound 4.

Scheme 4 Key mechanistic studies.

To support our mechanistic postulate Via a (Scheme 3), we conducted the following experiment. Compound (6) was independently synthesized from (2a), Via a Buchwald–Hartwig reaction with xantphos (obviously the imine suffered hydrolysis on the silica gel column to afford the aldehyde), and upon subjecting this to the conditions above, afforded (4) in 10% yield (Scheme 5). This reaction might occur via the tosylimine intermediate (8) (path a), that was predicted as part of the mechanistic pathway for Via a (Scheme 3), however a mechanism through path b (Scheme 5) involving the aldehyde intermediate (6) or its N-tosyl analogue, is also a possibility, but again the question of how the N–S cleavage occurs needs to be addressed.

Scheme 5 Further experimental studies to probe the mechanism.

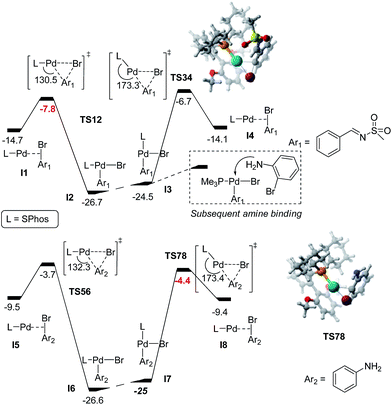
We then embarked on a computational study using DFT calculations to obtain further insight on the reaction mechanism. Except otherwise stated, the M06 functional,⁵¹ as implemented in the Gaussian 09 package was used.⁵² All reported values below are free energy in the gas phase (see Computational details). The first step is the oxidative addition (OA), which is typical in the Buchwald–Hartwig amination (and in any other palladium-catalyzed coupling reaction).^35–37 We decided to study; (1) the reasons behind the regioselective oxidative addition at the C–Br bond of (2) over (3) and (2) why the diazepine is favoured over the dibenzoaminopiperidine.

The OA step has been studied computationally in several coupling reactions, on many different systems.^53–55 SPhos has been studied as the ligand.⁵⁶ An extensive study looking at conformational aspects of the phosphane ligands (including SPhos) in the OA process has been recently published.⁵⁷ It should be noted that studying the regioselectivity of C–X oxidative addition in aromatic systems is a non-trivial task.^58–61 Despite the difficulties, some insights have been obtained to rationalize the selectivity for some reactions.^62–64 C–X bonds in simple aromatic systems (without heteroatoms) have been less studied.^61,65 The variation of the Bond Dissociation Energies (BDE) of the bonds involved is usually invoked to rationalize such selectivity. Nevertheless, BDE calculations are not infallible and can even be redundant in the case of strong catalyst/ligand interactions.⁶⁶ The general idea is that a combination of the two factors (i.e. the interactions between the catalyst and the organo-halide and the BDEs) are usually at play.^65–67 To better understand the regioselectivity in the OA of (2b), we performed some detailed calculations. We used the aldimine (2b), with the Ms-group, instead of Ts- or Ns to reduce the conformational complexity. The relative energy barriers are reported in Fig. 2. We assumed that, as in previous studies, that the active species in the OA step was the monoligated phosphane.⁵⁵ It was observed that both (I4) and (I8) were structurally and energetically very similar to (I1) and (I5), respectively. They differ in the sense that they are connected to different transition states, due to a different orientation of the ligand around the metal centre. The first point of interest was the observation that the starting adducts formed between the aldimine (2b) and the catalyst (I1) and (I4) were more stable by ca. 5 kcal mol⁻¹ than the adducts formed between bromoaniline (3a) and the catalyst (I5) and (I8). The short interatomic distances between the phosphane and the Ms-group might be responsible for this stabilizing effect. We calculated two transition states for each substrate. The P–Pd–C_ortho angle was different in the two transition states. In TS12 and TS56 it was ca. 130°, while in (TS34) and (TS78) the angles were significantly more obtuse, ca. 170°. The lowest energy transition state for the aldimine (TS_12) was lower than the lowest energy transition state for the bromoaniline (TS_78). The difference in energy of 3.4 kcal mol⁻¹, was consistent with the complete regioselectivity experimentally observed. Again, the short distances between the hydrogen atoms of the phosphane and the Ms-group might be responsible for this stabilization. Interestingly, the isomers with the Ph-group trans to the phosphane (I3) and (I7) are almost isoenergetic compared to the ones with the Ph-group trans to the vacant site. This is in sharp contrast with the calculation for the isomers reported by Barder et al.,⁵⁶ where the conformers with the Ph group trans in relation to the phosphane were destabilized by ca. 10 kcal mol⁻¹ (these complexes, contained a chloride instead of bromide, and a simple phenyl group instead of the aldimine (2)). Such destabilization was convincingly explained by the trans influence of the various ligands around the metal centre.^68,69 We suspected that the discrepancy observed in our case was partly due to the use of a functional which accounts better for the for van der Waals interactions between the substrate and the phosphane, so we calculated (I3) and (I7) with B3LYP (used in ref. 56) instead of M06 (that we used in this study). When using B3LYP, the energy difference between the two complexes increased to 4.6 kcal mol⁻¹ (the trans bromide to the phosphane was the most stable isomer). When we used B3LYP with a simple aryl group (with the imine and the Ms-group), the gap increased to 9.7 kcal mol⁻¹, consistent with the value obtained in ref. 56 (more details are given in the ESI†). This suggests that the interactions between the ligand and the Ms-group (short interatomic distances between the hydrogen of the phosphane and the –SO₂Me) contributes significantly to the stability of the complex, even off-setting, or compensating for the destabilization caused when the Ph group is trans to the phosphane. The subsequent step corresponding to the binding of bromoaniline to the palladium (represented in the dashed box in Fig. 2) was not calculated, but it is safe to assume that this process should be lower than 18.9 kcal mol⁻¹ (reverse oxidative addition from the Pd(II) complexes).

Fig. 2 Relative free energies for the oxidative addition step for (2b) and (3a), compared to the separated species (2b), (3a) and the Pd(0) catalyst) in kcal mol⁻¹. The lowest transition states are highlighted in red.

We then calculated the BDE values of the starting materials at the same level of theory as in the optimizations. We found that the C–Br bond of (3a) is 3.7 kcal mol⁻¹ stronger than the corresponding bond for (2b) (83.7 kcal mol⁻¹ and 80.0 kcal mol⁻¹ respectively). This energy difference nicely follows the energy difference between both substrates at the oxidative addition step. Interestingly, it is of a similar magnitude to the one previously reported in simpler aromatic systems when a C–X bond is positioned α to an imine unit in an aromatic ring.⁷⁰ Spin density calculations for the phenylimine radical showed that the radical is delocalized onto the C=N bond (see ESI†). This suggests that the presence of the C=N bond, even if not part of the aromatic ring, affects the C–X bond strength, when it is close to the aromatic ring. The delocalization does not reach the Ms-group.

A simplified catalytic cycle is depicted in Scheme 6, it follows the Via a pathway proposed in Scheme 3. The steps following the oxidative addition in the Buchwald–Hartwig amination are usually proposed to be: the binding of the amine, deprotonation by the base, and C–N bond formation (reductive elimination),^71–73 but are not considered in this study. Computation of the deprotonation step can be challenging, and some recent results suggest that what takes place at this stage might not be very straightforward.^74,75 From (I9), the C–Br bond of the bromoaniline is cleaved in a second oxidative addition process. (I10) is thus easily afforded, having a calculated energy barrier of 5.9 kcal mol⁻¹ compared to (I9).

Scheme 6 Proposed catalytic cycle for DBDA formation, with energy values of some intermediates and transition states. Values are in free energy, in kcal mol⁻¹, respective to (2b), (3a), and the Pd(0) catalyst.

We also examined the possibility of an oxidative addition at the N–S bond, but the transition state was found to be more than 17 kcal mol⁻¹ higher than the ones corresponding to cleavage of the C–Br bonds (the transition state structure is reported in the ESI†). This supports us in discarding Via b and c depicted in Scheme 3.

The last step of the reaction deserves special attention because it is crucial in the DBDA formation. Starting with (I10), two different ring closure (RC) pathways are possible; C–C bond formation would afford the dibenzoaminopiperidine (or hydrogenated acridine), whilst C–N bond formation delivers the final DBDA product. However, only the latter is observed experimentally. Such coupling at the N atom is not unprecedented. Related examples of indole formation, starting with an amine,⁷⁶ or an imine⁷⁷ (the reactive form is believed to be the enamine) through coupling at the nitrogen atom has already been reported.

We looked at all these possibilities, and some of the results are shown in Table 4.

Table 4 Final ring closure (RC). Free energy values (in kcal mol⁻¹) for C–N and C–C bond formations

Complex	Adduct^a	TS^a	Product^a
a Values compared to the starting reactants: (2a), (3b) and the Pd(0) catalyst.b Ms-group has abandoned the complex.c Ms-group is bound to the nitrogen atom.
RC_CN^b	−45.5	−40.0	−83.7
RC_CC^b	−44.9	−16.9	−34.2
RC_CN_Ms^c	−56.2	−23.1	−77.6

---

Complexes (RC_CN) and (RC_CC) (Table 4) will be expected if the Ms-group abandons the complex prior to ring closure. We observe that the C–N bond formation is much more accessible, with a transition state ca. 25 kcal mol⁻¹ lower than the one affording the hydrogenated acridine (complex RC_CC). Such a significant difference is fully consistent with the exclusive DBDA formation observed. We note that the starting complexes have very similar energies because their structures are virtually identical, with the nitrogen atom pointing towards the palladium. The fact that the transition states for both ring closures collapse towards the same structure is typical of a bifurcation pathway on the potential energy surface.⁷⁸ We also located the transition state corresponding to a C–N bond formation with the Ms-group still bound to the nitrogen: the value was found to be 33.1 kcal mol⁻¹ higher than (I10). A direct cyclisation with the Ms-group still bound to the nitrogen is thus much more energetically demanding than the same process without the leaving group. The leaving group thus appears to hinder the final cyclization. Despite several attempts, we could not locate a transition state for the Ms-departure from the nitrogen atom. Nevertheless, we located it for the model system, using the PMe₃. A high barrier of 40.8 kcal mol⁻¹ was calculated, which suggests that the departure of the Ms-group is non-trivial.

However, it must be noted that once the Ms-group has departed the complex, the final C–N bond formation cyclization is facile (see the low barrier for RC_CN in Table 4).

Conclusions

To conclude, a new catalytic method for synthesizing biologically relevant dibenzodiazepines (DBDA) has been reported. This new catalytic approach to the synthesis of DBDA offers an attractive alternative approach to other methods, even that of Tsvelikhovsky and Buchwald.³³ The main feature is that it is a one-step process with an aldimine substrate. Calculations indicate that the regioselectivity at the oxidative addition step is due to the better stabilities of the starting adducts formed with the aldimine and lower barriers than the ones corresponding to bromoanilines. The unusual formation of a 7-membered ring over the 6-membered ring at the final step of the catalytic cycle has been rationalized. We are currently working on the biological activity of these compounds for Alzheimer's disease.

Experimental

Computational details

Calculations were performed by DFT methods with the M06 functional,⁵¹ as implemented in the Gaussian 09 suite of program.⁵² The palladium and bromine atoms were described using the SDD effective core potential for the inner electrons and its associated basis set for the outer ones.⁷⁹ The standard 6-31G(d) basis set was used for all other atoms.^80,81 Stationary points were fully optimized without any symmetry restriction. Vibrational frequency calculations were performed to verify the nature of the stationary points (i.e. minima or transition states). Connectivity of the transition states was confirmed by relaxing the transition state structures towards both reactant and product sides. In the pictures, oxygen atoms are shown in red, phosphorus in orange, palladium in green, bromine in brown, nitrogen in blue, and sulfur in yellow.

General considerations

All the reagents were obtained from Aldrich, Fluka, Acros and Alfa Aeser. The solvents used were dried using current laboratory techniques.⁸² All the reagents applied in this work were used as received. All reactions with transition metals were conducted under a nitrogen atmosphere. Column chromatography was carried out on silica gel (sds, 70–200 μm). Thin layer chromatography (TLC) was carried out on aluminium backed Kiselgel 60 F254 plates (Merck). Plates were visualized either by UV light or with phosphomolybdic acid in ethanol. ¹H and ¹³C NMR spectra was recorded on a Bruker Avance III at 400 and 100 MHz, respectively, and the chemical shifts were quoted in parts per million (ppm) referenced to the appropriate non-deuterated solvent peak relative to 0.0 ppm for tetramethylsilane. Mass spectra (MS) using the ESI-TOF technique were obtained from the University of Vigo, C.A.C.T.I., Spain. The detailed procedures for the synthesis of compounds (2) are described in ESI.†

General procedure for the synthesis of the DBDA (4)

The reactions were performed under a nitrogen atmosphere using a Radleys® 12 position carousel reactor station. Pd(OAc)₂ (2.5 mol%), SPhos (5.0 mol%), o-bromoarylimines, o-bromoarylamines, Cs₂CO₃ (2.0 equiv.) and THF were added to the reaction tube. The reactions were performed at 100 °C for 18 h. The reactions were monitored by TLC, to follow the disappearance of the starting materials. After completion, the mixture was allowed to cool to room temperature. The reaction mixture was filtered with celite and the solvent removed under reduced pressure and then purified by column chromatography using 9 : 1 hexane/EtOAc, to give the pure compounds.

5H-Dibenzo[b,e][1,4]diazepine (4aa)⁸³. Yellow solid mp 124.0–124.5 °C. ¹H NMR (400 MHz, CDCl₃): δ 7.06–7.12 (m, 2H), 7.33–7.37 (m, 2H), 7.42–7.46 (m, 1H), 7.62–7.66 (m, 2H), 8.33 (dd, J = 6.6 and 2.0 Hz, 1H), 8.76 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 118.5 (C), 120.0 (CH), 126.3 (C), 127.2 (CH), 128.0 (CH), 128.5 (CH), 129.7 (CH), 133.0 (CH), 133.2 (CH), 133.4 (CH), 134.4 (C), 150.5 (C), 160.8 (HC=N) ppm. MS (ESI-TOF) m/z: 195.2 (M⁺ + H).

2-Fluoro-5H-dibenzo[b,e][1,4]diazepine (4ga). Yellow solid mp 107.2–108.8 °C. ¹H NMR (400 MHz, CDCl₃): δ 7.05–7.14 (m, 3H), 7.34–7.38 (m, 1H), 7.58–7.67 (m, 2H), 8.03–8.06 (m, 1H), 8.70 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 116.0 (d, J = 24 Hz, CH), 118.7 (C), 119.8 (CH), 120.2 (d, J = 23 Hz, CH), 127.6 (CH), 128.6 (CH), 133.3 (CH), 134.6 (d, J = 7.5 Hz, CH), 136.3 (C), 146.1 (C), 150.0 (C), 159.6 (HC=N), 162.3 (d, J = 239.7 Hz, C–F) ppm. MS (ESI-TOF) m/z: 213.21 (M⁺ + H).

2-Methoxy-5H-dibenzo[b,e][1,4]diazepine (4ea). Brown semi-solid. ¹H NMR (400 MHz, CDCl₃): δ 3.87 (s, 3H, OMe), 6.91–6.94 (m, 1H), 7.04–7.10 (m, 2H), 7.31–7.35 (m, 1H), 7.47–7.49 (m, 1H), 7.62–7.64 (m, 1H), 7.84–7.85 (m, 1H), 8.69 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 55.8 (OMe), 118.0 (CH), 119.9 (CH), 120.7 (CH), 127.2 (CH), 128.4 (C), 128.5 (CH), 132.6 (C), 133.1 (CH), 133.9 (CH), 134.0 (C), 134.8 (C), 150.2 (C), 160.6 (HC=N) ppm. MS (ESI-TOF) m/z: 225.27 (M⁺ + H).

3-Methoxy-5H-dibenzo[b,e][1,4]diazepine (4fa). Brown semi-solid. ¹H NMR (400 MHz, CDCl₃): δ 3.87 (s, 3H, OMe), 6.95–7.08 (m, 3H), 7.31–7.35 (m, 1H), 7.62–7.64 (m, 1H), 7.89–7.91 (m, 1H), 8.27–8.29 (m, 1H), 8.66 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 55.9 (OMe), 114.6 (CH), 118.1 (CH), 120.0 (CH), 124.9 (CH), 126.8 (C), 128.5 (CH), 128.9 (C), 130.6 (CH), 131.0 (C), 132.6 (C), 133.2 (CH), 156.8 (C), 159.9 (HC=N) ppm. MS (ESI-TOF) m/z: 225.27 (M⁺ + H).

3-Methoxy-5H-dibenzo[b,e][1,4]diazepin-2-ol (4ga). Colorless oil. ¹H NMR (400 MHz, CDCl₃): δ 3.96 (s, 3H, OMe), 4.06 (br s, 1H, OH), 5.68 (br s, 1H, NH), 7.03–7.09 (m, 3H), 7.31–7.35 (m, 1H), 7.62–7.64 (m, 1H), 7.91 (s, 1H), 8.62 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 56.5 (OMe), 114.5 (CH), 114.9 (CH), 120.0 (CH), 127.0 (CH), 128.5 (CH), 132.7 (C), 133.3 (CH), 144.2 (C), 145.5 (C), 150.3 (C), 150.6 (C), 151.8 (C), 160.1 (HC=N) ppm. MS (ESI-TOF) m/z: 241.27 (M⁺ + H).

8-(Trifluoromethyl)-5H-dibenzo[b,e][1,4]diazepine (4ab). Yellow semi-solid. ¹H NMR (400 MHz, CDCl₃): δ 7.10–7.12 (m, 1H), 7.37–7.46 (m, 2H), 7.59–7.67 (m, 2H), 7.90 (br s, 1H), 8.30–8.33 (m, 1H), 8.62 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 125.7 (q, J = 7.0 Hz, CH), 126.6 (CH), 127.3 (CH), 129.7 (q, J = 260.0 Hz, CF₃), 129.2 (C), 130.0 (q, J = 3.8 Hz, CH), 130.3 (q, J = 6.8 Hz, CH), 132.1 (q, J = 30.0 Hz, C–CF₃), 133.7 (CH), 133.9 (CH), 147.1 (C), 153.7 (C), 158.0 (C), 162.2 (HC=N) ppm. MS (ESI-TOF) m/z: 263.24 (M⁺ + H).

5H-Dibenzo[b,e][1,4]diazepine-7-carbonitrile (4ac). Yellow semi-solid. ¹H NMR (400 MHz, CDCl₃): δ 3.68 (br s, 1H, NH), 7.11 (d, J = 8.0 Hz), 7.38–7.48 (m, 2H), 7.63–7.67 (m, 2H), 7.93 (d, J = 1.6 Hz), 8.29 (dd, J = 2.0 and 7.8 Hz), 8.74 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 110.5 (C), 117.7 (C), 118.3 (C), 120.6 (CH), 126.7 (C), 128.1 (CH), 129.8 (CH), 132.5 (CH), 133.6 (CH), 133.7 (C), 133.8 (CH), 136.6 (CH), 154.7 (C), 162.5 (HC=N) ppm. MS (ESI-TOF) m/z: 219.24 (M⁺ + H).

7-Methyl-5H-dibenzo[b,e][1,4]diazepine⁸⁴ (4ad). White oil. ¹H NMR (400 MHz, CDCl₃): δ 2.36 (s, 3H, CH₃), 6.86–6.93 (m, 2H, ArH), 7.32–7.36 (m, 1H, ArH), 7.41–7.46 (m, 1H, ArH), 7.49.7.51 (m, 1H, ArH), 7.62–7.67 (m, 1H, ArH), 8.30–8.33 (m, 1H, ArH), 8.74 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 21.2 (Me), 115.0 (C), 120.7 (CH), 126.2 (CH), 128.0 (CH), 128.1 (CH), 129.6 (CH), 132.8 (CH), 132.9 (CH), 133.4 (CH), 134.4 (C), 138.7 (C), 150.2 (C), 160.5 (HC=N) ppm. MS (ESI-TOF) m/z: 209.27 (M⁺ + H).

7-Nitro-5H-dibenzo[b,e][1,4]diazepine (4ae). Yellow solid, mp 139.3–139.7 °C. ¹H NMR (400 MHz, CDCl₃): δ 7.40–7.46 (m, 2H), 7.67 (dd, J = 1.2 and 8.0 Hz, 1H), 7.82 (d, J = 8.8 Hz), 7.89 (d, J = 2.8 Hz), 7.96 (dd, J = 2.8 and 8.8 Hz), 8.31 (dd, J = 1.2 and 8.0 Hz), 8.82 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 114.6 (CH), 121.3 (CH), 126.0 (C), 126.8 (C), 128.1 (CH), 129.8 (CH), 133.6 (CH), 133.7 (C), 133.8 (CH), 133.9 (CH), 148.1 (C), 151.5 (C), 162.8 (HC=N) ppm. MS (ESI-TOF) m/z: 240.23 (M⁺ + H).

8-Fluoro-6-methyl-5H-dibenzo[b,e][1,4]diazepine (4af). Yellow solid, mp 78.4–79.0 °C. ¹H NMR (400 MHz, CDCl₃): δ 2.22 (s, 3H, CH₃), 6.69–6.95 (m, 1H), 7.21–7.23 (m, 1H), 7.36–7.45 (m, 2H), 7.54–7.66 (m, 1H), 8.27–8.29 (m, 1H), 8.67 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 29.8 (CH₃), 116.6 (d, J = 21.7 Hz, CH), 117.6 (d, J = 24.9 Hz, CH), 126.2 (C), 128.0 (CH), 129.2 (CH), 131.5 (C), 133.1 (CH), 133.4 (CH), 134.3 (C), 138.5 (C), 146.5 (C), 159.0 (d, J = 244.7 Hz, C–F), 165.1 (HC=N) ppm. MS (ESI-TOF) m/z: 227.26 (M⁺ + H).

8-Fluoro-2-methoxy-6-methyl-5H-dibenzo[b,e][1,4]diazepine (4ce). Yellow solid mp 68.5–69.2 °C. ¹H NMR (400 MHz, CDCl₃): δ 2.22 (s, 3H, CH₃), 3.88 (s, 3H, OMe). 6.91.6.98 (m, 2H), 7.21–7.24 (m, 1H), 7.51–7.53 (m, 1H), 7.80–7.81 (m, 1H), 8.63 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 19.3 (CH₃), 55.9 (OMe), 112.4 (CH), 116.5 (d, J = 21.7 Hz, CH), 117.1 (C), 117.4 (d, J = 26.9 Hz, CH), 120.8 (CH), 123.4 (C), 131.5 (d, J = 8.2 Hz, C), 134.1 (CH), 134.7 (d, J = 3.1 Hz, C), 146.4 (C), 159.0 (d, J = 244.6 Hz, C–F), 159.3 (C), 165.0 (HC=N) ppm. MS (ESI-TOF) m/z: 257.28 (M⁺ + H).

Procedure for the synthesis of the compound (5)

(E)-2-Bromo-N-(2-bromobenzylidene)aniline (5). The reaction was performed under a nitrogen atmosphere in two-necked flask. Pd(OAc)₂ (2.5 mol%), SPhos (5.0 mol%), o-bromobenzaldehyde (0.100 g, 0.54 mmol), o-bromoaniline (1 equiv.) Cs₂CO₃ (2 equiv.) and THF were added to the reaction flask. The reactions were performed at 100 °C for 18 h. The reactions were monitored by TLC, to follow the disappearance of the starting materials. After completion, the mixture was allowed to cool to room temperature. The reaction mixture was filtered with celite and the solvent removed under reduced pressure and after purification by column chromatography using 5 : 1 hexane/EtOAc, the title compound was obtained as a brown oil (0.092 g, 50%). ¹H NMR (400 MHz, CDCl₃): δ 7.67–7.77 (m, 2H), 7.86–7.89 (m, 1H), 8.06 (d, J = 8.0 Hz, 1H), 8.20 (d, J = 8.0 Hz, 1H), 8.58–8.63 (m, 2H), 9.29 (br s, 1H, HC=N) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 122.0 (CH), 122.4 (CH), 124.3 (C), 126.5 (C), 127.2 (CH), 127.6 (CH), 128.8 (CH), 128.9 (CH), 130.2 (CH), 131.2 (CH), 132.7 (C), 144.5 (C), 153.7 (HC=N) ppm. MS (ESI-TOF) m/z: 336.91 (⁷⁹Br₂), 338.91 (⁷⁹Br⁸¹Br); 340.91 (⁸¹Br₂).

Procedure for the synthesis of the compound (6)

2-(2-Bromophenylamino)benzaldehyde (6). The reaction was performed under a nitrogen atmosphere in two-necked flask. Pd(OAc)₂ (2.5 mol%), xantphos (5.0 mol%), o-bromobenzaldehyde (0.250 g, 1.4 mmol), o-bromoaniline (1 equiv.), Cs₂CO₃ (2 equiv.) and 1,4-dioxane were added to the reaction flask. The reactions were performed at 80 °C for 18 h. The reactions were monitored by TLC, to follow the disappearance of the starting materials. After completion, the mixture was allowed to cool to room temperature. The reaction mixture was filtered with celite and the solvent removed under reduced pressure and after purification by column chromatography using 9 : 1 hexane/EtOAc, the title compound was obtained as a yellow semi-solid (0.254 g, 68%). ¹H NMR (400 MHz, CDCl₃): δ 6.80 (t, J = 7.6 Hz, 1H), 6.90 (t, J = 7.6 Hz, 1H), 7.06 (d, J = 8.8 Hz, 1H), 7.20 (t, J = 7.6 Hz, 1H), 7.29 (t, J = 7.6 Hz, 1H), 7.41 (d, J = 8.0 Hz, 1H), 7.49–7.56 (m, 2H), 9.85 (br s, 1H, CHO), 9.97 (br s, 1H, NH) ppm. ¹³C NMR (100 MHz, CDCl₃): δ 113.4 (CH), 118.2 (CH), 118.4 (C), 120.3 (C), 123.7 (CH), 125.5 (CH), 128.0 (CH), 133.8 (CH), 135.6 (CH), 136.7 (CH), 138.6 (C), 146.7 (C), 194.3 (CHO) ppm. MS (ESI-TOF) m/z: 275.14 (⁷⁹Br); 277.14 (⁸¹Br).

Acknowledgements

This work was supported by INMOLFARM – Molecular Innovation and Drug Discovery, ALENT-07-0224-FEDER-001743, co-financed by FEDER through the INALENTEJO Program. AL and CSM are grateful for the award of a post-doc grant, DP a PhD grant and AG a research scholarship. We acknowledge funding from the Fundação para a Ciência e Tecnologia (FCT) for support through strategic project – PEst-OE/QUI/UI0619/2014. LabRMN University of Évora for the acquisition of the NMR spectra. The C.A.C.T.I. at the University of Vigo (Spain) is gratefully acknowledged for MS analysis.

Notes and references

1. A. Deiters and S. F. Martin, Chem. Rev., 2004, 104, 2199–2238.
2. L. J. Kricka and A. Ledwith, Chem. Rev., 1974, 74, 101–123.
3. P. Thansandote and M. Lautens, Chem.–Eur. J., 2009, 15, 5874–5883.
4. G. Chouinard, L. Annable, R. Fontaine and L. Solyom, Psychopharmacology, 1982, 77, 229–233.
5. R. J. Baldessarini and F. R. N. Frankenburg, N. Engl. J. Med., 1991, 324, 746–754.
6. http://www.who.int/medicines/publications/essentialmedicines/en/, retrieved 22 February 2015.
7. R. W. Buchanan, Schizophr. Bull., 1995, 21, 579–591.
8. M. Rowley, L. J. Bristow and P. H. Hutson, J. Med. Chem., 2001, 44, 477–501.
9. N. M. Richtand, J. A. Welge, A. D. Logue, P. E. Keck, S. M. Strakowski and R. K. McNamara, Neuropsychopharmacology, 2007, 32, 1715–1726.
10. G. Remington and S. Kapur, Psychopharmacology, 2000, 148, 3–15.
11. P. Seeman, H. C. Guan and H. H. M. Vantol, Nature, 1993, 365, 441–445.
12. J. Su, H. Q. Tang, B. A. McKittrick, D. A. Burnett, H. T. Zhang, A. Smith-Torhan, A. Fawzi and J. Lachowicz, Bioorg. Med. Chem. Lett., 2006, 16, 4548–4553.
13. T. K. Sasikumar, D. A. Burnett, H. Zhang, A. Smith-Torhan, A. Fawzi and J. E. Lachowicz, Bioorg. Med. Chem. Lett., 2006, 16, 4543–4547.
14. J. Sakaki, K. Konishi, M. Kishida, H. Gunji, T. Kanazawa, H. Uchiyama, H. Fukaya, H. Mitani and M. Kimura, Bioorg. Med. Chem. Lett., 2007, 17, 4808–4811.
15. J. Sakaki, M. Kishida, K. Konishi, H. Gunji, A. Toyao, Y. Matsumoto, T. Kanazawa, H. Uchlyama, H. Fukaya, H. Mitani, Y. Arai and M. Kimura, Bioorg. Med. Chem. Lett., 2007, 17, 4804–4807.
16. A. V. Joshua, S. K. Sharma, A. Strelkov, J. R. Scott, M. T. Martin-Iverson, D. N. Abrams, P. H. Silverstone and A. J. B. McEwan, Bioorg. Med. Chem. Lett., 2007, 17, 4066–4069.
17. S. Cassidy and J. Henry, Br. Med. J., 1987, 295, 1021–1024.
18. J. R. Donald, R. R. Wood and S. F. Martin, ACS Comb. Sci., 2012, 14, 135–143.
19. R. A. Smits, H. D. Lim, B. Stegink, R. A. Bakker, I. J. P. de Esch and R. Leurs, J. Med. Chem., 2006, 49, 4512–4516.
20. H. Y. Meltzer and S. R. McGurk, Schizophr. Bull., 1999, 25, 233–255.
21. J. A. Lieberman, T. S. Stroup, J. P. McEvoy, M. S. Swartz, R. A. Rosenheck, D. O. Perkins, R. S. E. Keefe, S. M. Davis, C. E. Davis, B. D. Lebowitz, J. Severe and J. K. Hsiao, N. Engl. J. Med., 2005, 353, 1209–1223.
22. N. Kaur and D. Kishore, Synth. Commun., 2014, 44, 1375–1413.
23. N. Della Ca', G. Maestri, M. Malacria, E. Derat and M. Catellani, Angew. Chem., Int. Ed., 2011, 50, 12257–12261.
24. K. M. El-Shaieb, A. A. Hassan and A. S. J. Abdel-Aal, J. Chem. Res., 2011, 592–594.
25. R. Z. Fu, X. X. Xu, Q. Dang and X. Bai, J. Org. Chem., 2005, 70, 10810–10816.
26. X. Xu, S. Guo, Q. Dang, J. Chen and X. Bai, J. Comb. Chem., 2007, 9, 773–782.
27. F. Shi, X. Xu, L. Zheng, Q. Dang and X. Bai, J. Comb. Chem., 2008, 10, 158–161.
28. X. Jiang, G. T. Lee, K. Prasad and O. Repic, Org. Process Res. Dev., 2008, 12, 1137–1141.
29. J. X. Yang, X. Che, Q. Dang, Z. L. Wei, S. Gao and X. Bai, Org. Lett., 2005, 7, 1541–1543.
30. J. Cairns, T. R. Clarkson, J. A. M. Hamersma and D. R. Rae, Tetrahedron Lett., 2002, 43, 1583–1585.
31. E. M. Beccalli, G. Broggini, G. Paladino and C. Zoni, Tetrahedron, 2005, 61, 61–68.
32. D. Tsvelikhovsky and S. L. Buchwald, J. Am. Chem. Soc., 2010, 132, 14048–14051.
33. D. Tsvelikhoysky and S. L. Buchwald, J. Am. Chem. Soc., 2011, 133, 14228–14231.
34. S. Fang, X. Niu, Z. Zhang, Y. Sun, X. Si, C. Shan, L. Wei, A. Xu, L. Feng and C. Ma, Org. Biomol. Chem., 2014, 12, 6895–6900.
35. B. H. Yang and S. L. Buchwald, J. Organomet. Chem., 1999, 576, 125–146.
36. For reviews see: C. S. Marques and A. J. Burke, Catalytic Arylation Methods – From the Academic Lab to Industrial Processes, Wiley-VCH, Weinheim, 2015; J. P. Wolfe, S. Wagaw, J. F. Marcoux and S. L. Buchwald, Acc. Chem. Res., 1998, 31, 805–818.
37. J. F. Hartwig, Angew. Chem., Int. Ed., 1998, 37, 2047–2067.
38. C. S. Marques and A. J. Burke, ChemCatChem, 2011, 3, 635–645.
39. C. S. Marques and A. J. Burke, Eur. J. Org. Chem., 2010, 1639–1643.
40. C. S. Marques and A. J. Burke, Eur. J. Org. Chem., 2012, 4232–4239.
41. D. S. Surry and S. L. Buchwald, Chem. Sci., 2011, 2, 27–50.
42. (a) D. S. Surry and S. L. Buchwald, Angew. Chem., Int. Ed., 2008, 47, 6338–6361; (b) P. Wagner, M. Bollenbach, C. Doebelin, F. Bihel, J.-J. Bourguignon, C. Salomé and M. Schmitt, Green Chem., 2014, 16, 4170–4178; (c) J. Hartwig, M. Kawatsura, S. I. Hauck, K. H. Shaughnessy and L. M. Alcazar-Roman, J. Org. Chem., 1999, 64, 5575–5580; (d) S. Lee, M. Jørgensen and J. F. Hartwig, Org. Lett., 2001, 3, 2729–2732; (e) M. S. Drive and J. F. Hartwig, J. Am. Chem. Soc., 1996, 118, 7217–7218; (f) J. P. Wolfe, S. Wagaw, J.-F. Marcoux and S. L. Buchwald, Acc. Chem. Res., 1998, 31, 805–818; (g) F. Wang, Z. Law, Y. Zhou, X. Bao and H. F. Schaefer, Chem.–Eur. J., 2015, 21, 4153–4161.
43. C. Meyers, B. U. W. Maes, K. T. J. Loones, G. Bal, G. L. F. Lemiere and R. A. Dommisse, J. Org. Chem., 2004, 69, 6010–6017.
44. J. P. Wolfe, H. Tomori, J. P. Sadighi, J. J. Yin and S. L. Buchwald, J. Org. Chem., 2000, 65, 1158–1174.
45. Metal-Catalyzed Cross-Coupling Reaction, ed. A. de Meijere and F. D. Diederich, Wiley-VCH, Weinheim, 2004.
46. C. A. Tolman, Chem. Rev., 1977, 77, 313–348.
47. C. S. Marques and A. J. Burke, Tetrahedron, 2013, 69, 10091–10097.
48. T. Kano, T. Yurino, D. Asakawa and K. Maruoka, Angew. Chem., Int. Ed., 2013, 52, 5532–5534.
49. M. Ciaccia and S. Di Stefano, Org. Biomol. Chem., 2015, 13, 646–654.
50. (a) R. J. Lundgren, K. D. Hesp and M. Stradiotto, Synlett, 2011, 2443–2458; (b) R. J. Lundgren, B. D. Peters, P. G. Alsabeth, K. D. Hesp and M. Stradiotto, Angew. Chem., Int. Ed., 2010, 49, 4071–4074.
51. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
53. M. Ahlquist, P. Fristrup, D. Tanner and P. O. Norrby, Organometallics, 2006, 25, 2066–2073.
54. Z. Li, Y. Fu, Q.-X. Guo and L. Liu, Organometallics, 2008, 27, 4043–4049.
55. K. Vikse, T. Naka, J. S. McIndoe, M. Besora and F. Maseras, ChemCatChem, 2013, 5, 3604–3609.
56. T. E. Barder, M. R. Biscoe and S. L. Buchwald, Organometallics, 2007, 26, 2183–2192.
57. C. L. McMullin, N. Fey and J. N. Harvey, Dalton Trans., 2014, 43, 13545–13556.
58. S. Schroter, C. Stock and T. Bach, Tetrahedron, 2005, 61, 2245–2267.
59. S. T. Handy and Y. N. Zhang, Chem. Commun., 2006, 299–301.
60. I. J. S. Fairlamb, Chem. Soc. Rev., 2007, 36, 1036–1045.
61. D. Sadowsky, K. McNeill and C. J. Cramer, Environ. Sci. Technol., 2013, 47, 14194–14203.
62. X. Dai, Y. Chen, S. Garrell, H. Liu, L.-K. Zhang, A. Palani, G. Hughes and R. Nargund, J. Org. Chem., 2013, 78, 7758–7763.
63. S. Malhotra, P. S. Seng, S. G. Koenig, A. J. Deese and K. A. Ford, Org. Lett., 2013, 15, 3698–3701.
64. W. A. Herrebout, N. Nagels, S. Verbeeck, B. J. van der Veken and B. U. W. Maes, Eur. J. Org. Chem., 2010, 3152–3158.
65. A. Aballay, E. Clot, O. Eisenstein, M. T. Garland, F. Godoy, A. H. Klahn, J. C. Munoz and B. Oelckers, New J. Chem., 2005, 29, 226–231.
66. Y. Garcia, F. Schoenebeck, C. Y. Legault, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 6632–6639.
67. C. Y. Legault, Y. Garcia, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 12664–12665.
68. J. P. Stambuli, C. D. Incarvito, M. Buhl and J. F. Hartwig, J. Am. Chem. Soc., 2004, 126, 1184–1194.
69. T. G. Appleton, H. C. Clark and L. E. Manzer, Coord. Chem. Rev., 1973, 10, 335–422.
70. C. Barckholtz, T. A. Barckholtz and C. M. Hadad, J. Am. Chem. Soc., 1999, 121, 491–500.
71. L. M. Alcazar-Roman, J. F. Hartwig, A. L. Rheingold, L. M. Liable-Sands and I. A. Guzei, J. Am. Chem. Soc., 2000, 122, 4618–4630.
72. U. K. Singh, E. R. Strieter, D. G. Blackmond and S. L. Buchwald, J. Am. Chem. Soc., 2002, 124, 14104–14114.
73. S. Shekhar, P. Ryberg, J. F. Hartwig, J. S. Mathew, D. G. Blackmond, E. R. Strieter and S. L. Buchwald, J. Am. Chem. Soc., 2006, 128, 3584–3591.
74. K. H. Hoi, S. Calimsiz, R. D. J. Froese, A. C. Hopkinson and M. G. Organ, Chem.–Eur. J., 2011, 17, 3086–3090.
75. K. H. Hoi, S. Calimsiz, R. D. J. Froese, A. C. Hopkinson and M. G. Organ, Chem.–Eur. J., 2012, 18, 145–151.
76. M. C. Willis, G. N. Brace, T. J. K. Findlay and I. P. Holmes, Adv. Synth. Catal., 2006, 348, 851–856.
77. (a) J. Barluenga, A. Jimenez-Aquino, C. Valdes and F. Aznar, Angew. Chem., Int. Ed., 2007, 46, 1529–1532; (b) K. R. Roesch, H. Zhang and R. C. Larock, J. Org. Chem., 2001, 66, 8042–8051.
78. D. H. Ess, S. E. Wheeler, R. G. Iafe, L. Xu, N. Celebi-Olcum and K. N. Houk, Angew. Chem., Int. Ed., 2008, 47, 7592–7601.
79. D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141.
80. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. Defrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
81. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
82. W. L. F. A. Perrin, Purification of Laboratory Chemicals, Butterworth Heinemann, Oxford, 4th edn, 1996.
83. P. S. Chandrachood and N. S. Narasimhan, Synthesis, 1979, 8, 589–590.
84. M. Yang, L. Wu, D. She, H. Hui, Q. Zhao, M. Chen and G. Huang, Synlett, 2008, 3, 448–452.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra19599c

---