Prediction of stoichiometric PoH_n compounds: crystal structures and properties

Abstract

Stable compounds, crystal structures and properties of polonium hydrides have been systematically investigated through the first-principles calculations based on the density functional theory. With the increasing pressure, several stoichiometries (PoH, PoH₂, PoH₄ and PoH₆) are predicted to be stabilized in an excess hydrogen environment. Except for PoH, other stable stoichiometries exhibit intriguing structural character with the appearance of H₂ units. Moreover, the electronic band structure and projected density of states (PDOS) demonstrate that these energetically stable phases are metallic. The application of the Allen–Dynes modified McMillan equation with the calculated electron-phonon coupling parameter reveals that PoH₄ is a superconductor with a critical temperature T_c of 41.2–47.2 K at 200 GPa.

---

1. Introduction

Over the past ten years, hydrogen-rich compounds have been the focus of research for their potential to become extraordinary high-temperature superconductors at lower pressures which are accessible to current experiments. The elements of group VIA, which include oxygen, sulfur, selenium, tellurium and polonium, present many interesting properties under pressure, such as the metallic phases of O₂, S, Se and Te were found to be superconducting in experiment, with a transition temperature T_c of 0.6, 10, 5 and 4.5 K, respectively.^1–5 Recently, group VIA hydrides were expected to metalize at lower pressures with potential superconductivity. Remarkably, the Im3̄m phase of H₃S with outstanding high T_c of 191–204 K at 200 GPa was first predicted by our group using the ab initio calculation method.⁶ It is spectacular that the superconductivity in H₂S sample with T_c of 190 K above 150 GPa was observed by Eremets et al. in experiment,⁷ which is speculated that the high T_c likely associates with our predicted H₃S. Later, we theoretically reported that H₂S really decomposes into S and H₃S above 43 GPa, and H₃S is stable at least up to 300 GPa, which proved that high T_c in H₂S sample observed experimentally comes from H₃S.⁸ Other theoretical studies also confirmed our results using different structural search techniques.^9,10 Recently, selenium (Se) hydrides and tellurium (Te) hydrides were theoretically predicted to exhibit T_c in the range of 40–131 K and 46–104 K at megabar pressures, respectively.^11–13 These dense hydrides has reignited great interest in chalcogen hydrogen-rich compounds.

Polonium (Po) is the only metal element in the group VIA, which possesses the simple cubic (sc) structure at ambient conditions. Based on the high-T_c superconductivity of other chalcogenide hydrides, polonium hydrides might also exhibit high superconducting transition temperature at high pressures. It is well established that the application of high pressure can influence the physical and chemical properties of matter, and lead to the formation of unprecedented phases or complexes with novel characters. Such as, the superconductivity of SiH₄ and PtH were experimentally confirmed at high pressure.^14–16 Other new unusual stoichiometries were predicted to form at high pressure in theory (e.g. LiH₆, NaH₉, KH₆, RbH₅, CsH₃ and so on).^17–21 Therefore, the investigation of polonium hydrides under high pressure might provide us interesting information.

In this article, the ground-state structures of Po–H system over a range of pressures were explored by using the recently fast-developed evolutionary algorithm Universal Structure Predictor: Evolutionary Xtallography (USPEX).^22–24 Moreover, we investigate the optimum static structures as a function of pressure, their dynamical stability, the corresponding electronic band structures and superconductivity of Po–H system. Our results show that except for PoH, other stable stoichiometries have H₂ units. Furthermore, all the stable polonium hydrides are found to be metallic, and the superconducting critical temperature T_c values of PoH, PoH₄, and PoH₆ are 0.14–0.65 K, 41.1–47.2 K, and 2.65–4.68 K at 300, 200 and 200 GPa, respectively.

2. Computational method

The searches for stable high pressure structures of the PoH_n (n = 1–6) system were performed through the evolutionary algorithm, implemented in the USPEX code.^22–24 Structure predictions were implemented at 50, 100, 200, and 300 GPa with 1–4 formula units (f.u.). Each structure was fully relaxed to an energy minimum using density functional theory with the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA)²⁵ implemented in the Vienna ab initio simulation package VASP code.²⁶ The hybrid functional of Heyd, Scuseria, and Ernzerhof (HSE06)^27,28 was also used to verify the results of band structures with GGA function. We optimized predicted stable structures at higher accurate level. A plane-wave basis set cutoff of 800 eV and a Brillouin zone sampling grid of spacing 2π × 0.03 Å⁻¹ were chose, which ensures total energy convergence better than 1 meV per atom. The all-electron projector augmented wave method (PAW)²⁹ is adopted with the cut-off radius of 0.8 a.u. and 2.1 a.u. for H (1s²) and Po (6s²6p⁴), respectively. In the geometrical optimization, all forces on atoms were converged to less than 0.005 eV Å⁻¹. The lattice dynamics were performed using the supercell approach³⁰ as implemented in PHONOPY program.³¹ The electron–phonon coupling (EPC) for superconducting properties of stable compounds have been computed with QUANTUM-ESPRESSO.³² Convergence tests provide a suitable value of 80 Ry kinetic energy cutoff. The q-point mesh in the first BZ of 4 × 4 × 2 for P6₃/mmc (PoH), 5 × 5 × 2 for C2/c (PoH₄), and 3 × 3 × 3 for C2/m (PoH₆) structures were used in the Brillouin zone.

3. Results and discussion

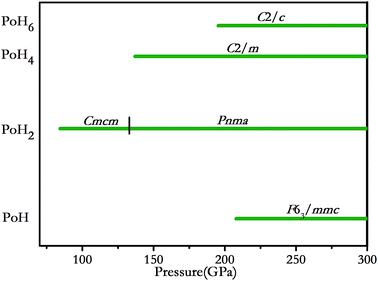
We explored polonium hydrides with hydrogen-rich contents through the evolutionary algorithm USPEX. The calculations were performed at 50–300 GPa with considering simulation sizes ranging from one to four formula units (f.u.) for PoH_n (n = 1, 2, 3, 4, 5, 6). Our calculations give convex hulls on the formation enthalpy of the Po–H system with H-rich stoichiometry from 50 to 300 GPa, as shown in Fig. 1. The structures on the convex hull are thermodynamically stable and they may be experimentally synthesized in principle, whereas those above it are metastable. The essential information can be summarized as follows: (i) at 100 GPa, PoH₂ has the most negative enthalpy out of all the structures that we examined; which can be synthesized using Po and H₂ by the reaction Po + H₂ → PoH₂; (ii) when pressure is increased up to 150 GPa, PoH₂ is still the global minimum stoichiometry. And PoH₄ also falls on the convex hull, which suggests that it might be synthesized via the reaction PoH₂ + H₂ → PoH₄, and it keeps stable up to 300 GPa; (iii) at 200 GPa, PoH₂, PoH₄ and PoH₆ stoichiometries are all found to lie on the hull; (vi) with increasing pressure to 250 GPa, another stable stoichiometry of PoH appears on the convex hull, which can be formed by the reaction PoH₂ + Po → 2PoH₂; (v) at 300 GPa, except for PoH₃ and PoH₅, all the stoichiometries become stable and emerge on the hull. The stable pressure ranges of predicted PoH, PoH₂, PoH₄ and PoH₆ together with Po and H₂ (ref. 33 and 34) are depicted in Fig. 2. At 84.5 GPa, the Cmcm phase of PoH₂ becomes stable and remains up to 133 GPa. Then the Pnma-PoH₂ becomes energetically favorable. PoH₄ (space group C2/c), PoH₆ (space group C2/m) and PoH (space group P6₃/mmc) become stable at 137, 195.5 and 208 GPa, respectively.

Fig. 1 The enthalpies of formation (ΔH_f, in eV per atom) for Po–H system with respect to Po and H at 50, 100, 150, 200, 250 and 300 GPa.

Fig. 2 The phase diagram of Po–H system in the pressure range from 70 to 300 GPa.

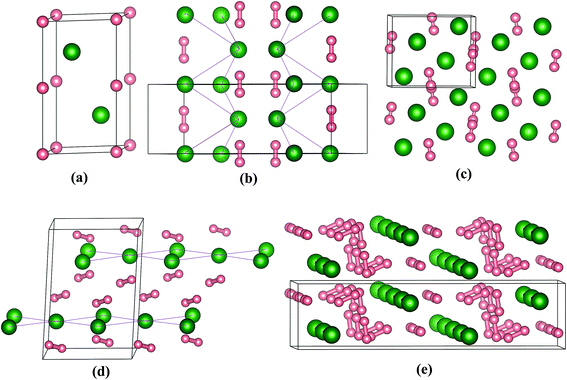
The crystal structures motifs of stable stoichiometries are depicted in Fig. 3, which shows that all structures contain H₂ units exception of PoH. We think that as the electronegativity value (2.0) of Po is smaller than H (2.2), charges transfer from Po to H. For PoH compound, the content of H is relative small, and the interaction of Po–H is enough to make the PoH stoichiometry stable. While for PoH_2,4,6, the content of H is more, H atoms are tend to form H₂ units to decrease material energy. Therefore, the H₂ units are present in PoH_2,4,6 (which contain more H), while H₂ units don't appear in PoH. From our calculations, the predicted energetically favored structure of PoH is P6₃/mmc at 300 GPa (Fig. 3a), and it is isostructural with TeH.¹³ The PoH₂ stoichiometry has two structures with Cmcm and Pnma space group at 50 and 300 GPa, respectively. To better describe the structural feature and to prevent misunderstanding, we connected the Po atoms with a purple straight line, as shown in Fig. 3b and d. While for the cases of PoH₂-Pnma, PoH₄-C2/c, and PoH₆-C2/m structures (Fig. 3b–e), some H atoms are existent in form of H₂ units and form bonds, which is due to the distances of H–H is in the range of 0.793–0.818 Å. For Cmcm structure, Po atoms form three-dimensional network (Fig. 3b), while in Pnma phase, Po atoms form a distorted bcc lattice (Fig. 3c). Moreover, quasi-molecular H₂ units are found with the distance of H–H 0.793 Å (50 GPa in Cmcm) and 0.841 Å (200 GPa in Pnma), respectively. For PoH₄ stoichiometry (Fig. 3d), it posses C2/c symmetry at 200 GPa, where Po atoms built up 2D layers and the H₂ units have H–H distance of 0.818 Å. Turning to the richest-H₂ stoichiometry PoH₆, it has a monoclinic C2/m space group at 200 GPa with chain Po atoms and H₂ units, as shown in Fig. 3e. By observing the high pressure structural feature for the chalcogenide group hydrides, we discovered that some hydrogen are existent in form of H₂ unit in S–H,⁶ Se–H,¹¹ Te–H¹³ and Po–H systems. Calculated structural parameters of the predicted stable structures for Po–H compounds at the selected pressure are displayed in Table S1.† It is necessary to determine the dynamical stability of structures. Fig. 4 presents the calculated phonon band dispersions and projected phonon density of states (PHDOS) for PoH-P6₃/mmc, PoH₂-Pnma, PoH₄-C2/c, and PoH₆-C2/m. They are all dynamical stability, as there are no imaginary phonon mode in the entire Brillouin zone. In addition, we see that there exist a distinguish between PoH and PoH_2,4,6, which is attributed to that PoH_2,4,6 posses H₂ units. For the former (Fig. 4a), the phonon band dispersions vibrational modes can be divided into two parts, low energy phonon modes are mainly from Po atoms, whereas modes with high frequency region are associated with H atoms. For the later (Fig. 4b–d), the vibrational modes can be separate into three regions. The low-energy region, the intermediate-frequency region and high frequencies are dominated by Po atoms, H⋯Po⋯H vibrations and H₂ units, respectively.

Fig. 3 The selected stable phases for Po–H system. Green atoms depict Po, while pink atoms present H, (a) PoH-P6₃/mmc at 300 GPa, (b) PoH₂-Cmcm at 50 GPa, (c) PoH₂-Pnma at 300 GPa, (d) PoH₄-C2/c at 200 GPa and (e) PoH₆-C2/m at 200 GPa.

Fig. 4 (a–d) The phonon band structure and projected phonon DOS charts for PoH-P6₃/mmc, PoH₂-Pnma, PoH₄-C2/c and PoH₆-C2/m at different pressure, respectively.

Band structure and projected density of states (DOS) at different pressures for PoH, PoH₂, PoH₄ and PoH₆ in the P6₃/mmc, Pnma, C2/c and C2/m phases were calculated, as displayed in Fig. 5. We clearly see that all the above structures exhibit metallic feature with overlap between the conduction and valence bands. For the simplest stoichiometry PoH-P6₃/mmc structure and PoH₂-Pnma phase, the Po-p state predominates the energy range from −10 to 5 eV, and there exist strong hybridization between Po-p and H-s states (−10 to −15 eV), as can be seen in Fig. 5a and b. For PoH₄, we can see that Po-s, Po-p, and H-s orbits dominate the Fermi level (Fig. 5c). For H-rich C2/m of PoH₆, at the Fermi level a strong DOS peak is observed in Fig. 5d, which originates from Po-p and H-s electrons. Note that, at Fermi level the Po-p is mainly dominated in Po–H system, which is similar to Se–H and Te–H systems. And this same behavior is attributed to their isoelectronic nature.^11,13 As we know, the GGA function underestimate the band gap, so we calculate band structures of PoH-P6₃/mmc and PoH₂-Pnma phases with the hybrid functional HSE06 method. It is shown that the results for the GGA and HSE calculations were almost identical, except that the band structures move down in HSE06 (Fig. S1†).

Fig. 5 Electronic band structure and partial density of states (PDOS). (a) PoH-P6₃/mmc at 300 GPa, (b) PoH₂-Pnma at 200 GPa, (c) PoH₄-C2/c at 200 GPa and (d) PoH₆-C2/m at 200 GPa.

To observe the possible superconductivity of PoH-P6₃/mmc, PoH₂-Pnma, PoH₄-C2/c and PoH₆-C2/m, we investigate the electron–phonon coupling (EPC) parameter λ, the logarithmic average phonon frequency ω_log, and the Eliashberg phonon spectral function α²F(ω) to explore the possible superconductivity for PoH-P6₃/mmc, PoH₂-Pnma, PoH₄-C2/c and PoH₆-C2/m at different pressures. The obtained EPC parameter λ is 0.33 for PoH (300 GPa), 0.19 for PoH₂ (200 GPa), 1.08 for PoH₄ (200 GPa) and 0.43 for PoH₆ (200 GPa), while the calculated ω_log from the phonon spectrum reach 806, 713, 603 and 836 K, respectively. The superconducting critical temperature T_c of Po–H system can be estimated by using the Allen–Dynes-modified McMillan equation³⁵ with the calculated logarithmic average frequency ω_log and the Coulomb pseudopotential μ* (0.1–0.13). The calculated T_c for PoH-P6₃/mmc, PoH₂-Pnma, PoH₄-C2/c and PoH₆-C2/m are 0.14–0.65 K at 300 GPa, 0 K at 200 GPa, 41.1–47.2 K at 200 GPa and 2.25–4.68 K at 200 GPa, respectively. We also calculated T_c for PoH₄-C2/c as a function of pressure. The values of ω_log, N(E_f), λ and T_c are summarized in Table S2.† As pressure increased, the resulting ω_log and T_c reach up to 804.2 K and 45.7–53.6 K at 250 GPa, respectively. However, both N(E_f) and λ parameters decrease with increasing pressure. The results indicated that the raising ω_log mainly causes the positive pressure dependence of T_c.

Fig. 6 shows the evaluated Eliashberg phonon spectral function α²F(ω) and the partial electron–phonon integral λ(ω) for PoH-P6₃/mmc, PoH₄-C2/c and PoH₆-C2/m to understand the origin of λ. Taken altogether, the electron–phonon integral has two regions low and high frequency in the above structures. For P6₃/mmc structure of PoH at 300 GPa (Fig. 6a), the low-frequency modes below 10 THz, contributing 46% of the total value λ, come from Po vibrations, whereas high frequency modes above 36 THz associated with H atoms provide a contribution 54% in total EPC parameter λ. For the C2/c phase of PoH₄ at 200 GPa (Fig. 6b), Po vibrations dominate the low frequency region and contribute approximately 39.3% in total λ. The intermediate-frequency vibrational modes from H⋯Po⋯H contribute 55.1% to the λ. And the remaining 5.6% of λ is from the H₂ vibrations. In the same way, for PoH₆-C2/m at 200 GPa (Fig. 6c), the Po, H⋯Po⋯H and H₂ vibration modes account for 25.5%, 68.3% and 7.2% of λ, respectively. Note that, in the PoH-P6₃/mmc which contains Po and H atom, the λ is mainly contributed from H vibrational modes. For the PoH₄-C2/c and PoH₆-C2/m, possessing H₂ units, the low and intermediary modes are mostly constitute of the λ, while the high frequencies of H₂ make small contributions to λ. The superconductive mechanism of PoH_4,6 is similar to TeH₄ (ref. 13) that contain similar H₂ units.

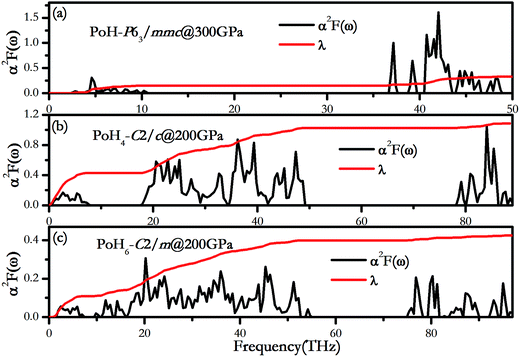Fig. 6 The Eliashberg phonon spectral function α²(ω) and the partial electron–phonon integration λ(ω). (a) PoH-P6₃/mmc at 300 GPa, (b) PoH₄-C2/c at 200 GPa and (c) PoH₆-C2/m at 200 GPa.

4. Conclusions

In summary, we explore the structures, phase diagram and superconductivity of polonium hydrides under pressure using ab initio calculations. The polonium hydrides become thermodynamically stable with respect to decomposition into the Po and H above 84.5 GPa. Upon further compression and in the excess hydrogen environment, PoH, PoH₂, PoH₄ and PoH₆ hydrides become thermodynamically preferred. Except for PoH-P6₃/mmc, a remarkable feature of the predicted stable structures is the presence of H₂ units. Electron–phonon coupling calculations show that the T_c of PoH-P6₃/mmc, PoH₄-C2/c, and PoH₆-C2/m are 0.14–0.65 K at 300 GPa, 41.1–47.2 K at 200 GPa and 2.25–4.68 K at 200 GPa, respectively. Our results provide a better understanding of the pressure-induced phase diagram and superconductivity of Po–H system, which has major implications for investigating other hydrides under pressure.

Acknowledgements

This work was supported by the National Basic Research Program of China (No. 2011CB808200), National Natural Science Foundation of China (No. 51572108, 11204100, 11504127, 11504127, 11404134), Program for Changjiang Scholars and Innovative Research Team in University (No. IRT1132), National Found for Fostering Talents of basic Science (No. J1103202). China Postdoctoral Science Foundation (2012M511326, 2013T60314, and 2014M561279). Graduate Innovation Fund of Jilin University (2015102). Parts of calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.

References

1. K. Shimizu, K. Suhara, M. Ikumo, M. Eremets and K. Amaya, Nature, 1998, 393, 767–769.
2. F. Bundy and K. Dunn, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 3157–3164.
3. Y. Akahama, M. Kobayashi and H. Kawamura, Solid State Commun., 1992, 84, 803–806.
4. V. V. Struzhkin, R. J. Hemley, H.-K. Mao and Y. A. Timofeev, Nature, 1997, 390, 382–384.
5. E. Gregoryanz, V. Struzhkin, R. Hemley, M. Eremets, H.-K. Mao and Y. Timofeev, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 064504.
6. D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968.
7. A. Drozdov, M. Eremets and I. Troyan, arXiv preprint arXiv:1412.0460, 2014.
8. D. Duan, X. Huang, F. Tian, D. Li, H. Yu, Y. Liu, Y. Ma, B. Liu and T. Cui, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 180502.
9. N. Bernstein, C. Hellberg, M. Johannes, I. Mazin and M. Mehl, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 91, 060511.
10. I. Errea, M. Calandra, C. J. Pickard, J. Nelson, R. J. Needs, Y. Li, H. Liu, Y. Zhang, Y. Ma and F. Mauri, arXiv preprint arXiv:1502.02832, 2015.
11. S. Zhang, Y. Wang, J. Zhang, H. Liu, X. Zhong, H. Sonf, L. Zhang and Y. Ma, Sci. Rep., 2015, 5, 15433.
12. J. A. Flores-Livas, A. Sanna and E. Gross, arXiv preprint arXiv:1501.06336, 2015.
13. X. Zhong, Y. Wang, H. Liu, S. Zhang, G. Yang, L. Zhang and Y. Ma, arXiv preprint arXiv:1503.00396, 2015.
14. M. Eremets, I. Trojan, S. Medvedev, J. Tse and Y. Yao, Science, 2008, 319, 1506–1509.
15. T. Scheler, O. Degtyareva, M. Marqués, C. L. Guillaume, J. E. Proctor, S. Evans and E. Gregoryanz, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 214106.
16. X. J. Chen, V. V. Struzhkin, Y. Song, A. F. Goncharov, M. Ahart, Z. Liu, H. K. Mao and R. J. Hemley, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20–23.
17. E. Zurek, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17640–17643.
18. P. Baettig and E. Zurek, Phys. Rev. Lett., 2011, 106, 237002.
19. D. Zhou, X. Jin, X. Meng, G. Bao, Y. Ma, B. Liu and T. Cui, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014118.
20. J. Hooper and E. Zurek, Chem.–Eur. J., 2012, 18, 5013–5021.
21. A. Shamp, J. Hooper and E. Zurek, Inorg. Chem., 2012, 51, 9333–9342.
22. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
23. A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237.
24. A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
28. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
30. K. Parlinski, Z. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063.
31. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
32. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
33. A. Rubio-Ponce, J. Morales and D. Olguín, in Advances in the Theory of Quantum Systems in Chemistry and Physics, Springer, 2012, pp. 119–127.
34. C. J. Pickard and R. J. Needs, Nat. Phys., 2007, 3, 473–476.
35. P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 905–922.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra19223d

---