[TM₁₃@Bi₂₀]⁻ clusters in three-shell icosahedral matryoshka structure: being as superatoms

Abstract

Using the density functional theory (DFT) method, the 33-atom intermetalloid [TM₁₃@Bi₂₀]⁻ clusters (TM = 3d, 4d), which are composed of Bi₂₀ pentagonal dodecahedra surrounding TM₁₂ icosahedra with a single TM atom at the center, have been systematically examined to explore the possibility of clusters being as superatoms. The results show that most TM₁₃ clusters can be attractively encapsulated into Bi₂₀ cage to form a stable core–shell configuration, exhibiting an interesting progression of thermal stability along the 3d and 4d periods. Taking into account the structural stability (binding energy, embedding energy, and core–shell interaction) as well as the chemical stability (HOMO–LUMO gap), we proposed that [TM₁₃@Bi₂₀]⁻ clusters with Ti and Mn doping in 3d series (Zr and Ag doping in 4d series) are specially stable and to be the protyle superatoms. For such systems, the molecular orbital shapes and energy alignments are in analogy with the atomic patterns, coinciding the general characters of superatomic orbitals. The closed core superatomic shell together with the partially-filled valence superatomic shell configuration leads to magnetic moment in stable [TM₁₃@Bi₂₀]⁻, e.g., [Mn₁₃@Bi₂₀]⁻ cluster with the half-filled subshell can be assigned as a magnetic superatom owning to its modest HOMO–LUMO gap of 0.37 eV and large magnetic moment of 36 μ_B. The exchange-splitting in TM-3d states is found to be the driving force for the improvement of exchange-splitting of superatomic states.

---

1 Introduction

One of the most exciting developments in cluster science is the finding that electronic states in specific clusters can be reasonably described by a nearly confined free electron gas in a spherically symmetric potential, and their unusual stability and chemical reactivities can be understood in terms of the spherical shell jellium model.^1–3 Such novel clusters, named as the superatoms,⁴ can mimic elemental atoms and have the potentials to construct a three-dimensional periodic table on the basis of the difference between its valence electron count and the number of electrons required to fill the nearest superatomic shell.^5,6 In particular, utilizing these artificial clusters (superatoms) as the building-blocks, one could design new materials with the desired characteristics.^4–8 Like free atom, superatomic electronic states are proposed to bunch into several supershells of 1S²1P⁶1D¹⁰2S²1F¹⁴2P⁶1G¹⁸2D¹⁰…, much in the same way as 1s²2s²2p⁶3s²3p⁶3d¹⁰… in free atoms but in different combination of quantum numbers and orbital sequences. Unlike free atom, the superatomic orbital (superorbital) spans over multiple atoms and the filling of orbitals does not usually exhibit Hund's rule. The essential idea of superatom is that specific stable cluster would exhibit similar chemical patterns of free atom if it has analogous valence shells with free atom.

The first step toward the development of superatoms is to identify the stable motifs, understand electronic features, and control their stabilities. Since the valance electrons in simple-metal clusters can be universally treated as metallic or more precisely as a confined nearly free electron gas, intensive investigations have been performed on small Al clusters^9–17 and Au clusters (or on their charged, doped, or ligated counterparts),^17–23 so as to highlight the fillings of electronic shells and hence to design new superatoms. A popular example is Al₁₃ superatom in configuration of 1S²1P⁶1D¹⁰2S²1F¹⁴2P⁵, which behaves like a halogen atom and exhibits a high electron affinity.¹¹ However, due to the structural distortions stemmed from the Jahn–Teller effect,²⁴ the filling of electronic orbitals in an ordinary superatom does not follow the Hund's rule of maximizing spin, and superatoms always favor nonmagnetic character with the paired electrons. These observations inspire an important issue whether nonmagnetic superatoms could be extended to magnetic species, with the intrinsic spin moments originating from superatom shells or with the introduced spin moments originating from localized atomic d states, i.e., how to tune the magnetic properties of superatoms? According to the employed method commonly for designing magnetic materials, single transition-metal atom (usually 3d or 4d TM atom) was extensively encapsulated into small simple-metal clusters, where host matrixes are composed of elements of group-IA (Li,²⁵ Na,^26–29 K,²⁹ Cs^27,29), group-IIA (Mg,^30–33 Ca,³⁴ Sr,^35,36), group-IIIB (Al,^11–13,17 Ga,^17,37), and group-IVB (Si,^38–40 Ge,^40,41 Sn,^40,41 Pb^42,43). The prototype of magnetic superatom is V-alkali clusters (VLi₈, VNa₈ and VCs₈) in configuration of 1S²1P⁶1D⁵, which can mimic a manganese atom and show a large spin magnetic moment of 5 μ_B.^25–27 So far, it is generally accepted that in magnetic superatoms, atomic d-state electrons (or superatomic D states) localized on TM sites would provide spin magnetic moment, while the delocalized s, p-valence electrons of simple-metal atoms and of TM atom would fully occupy diffuse superatomic S, P states and provide superatomic stability. In addition, under the consideration that stable superatoms can compose superatomic molecules by sharing their valence pairs, alternative efforts have been devoted to superatomic molecules to explore the promising hints for designing novel superatom-assembling materials.^22,32,44 Very recently, the newly constructed Li₁₄, Li₁₀, Li₈ clusters are proposed to be analogues to conventional F₂, N₂, CH₄ molecules owning to the similar exhibitions both in molecular-orbital diagrams and bonding-patterns.⁴⁴

Following the original motivation for developing new superatoms, spherical core–shell structures by placing small cluster into large cage at high symmetry have been designed to rich superatom family, such as [As@Ni₁₂@As₂₀]³⁻ and [Sn@Cu₁₂@Sn₂₀]¹²⁻ in bulk A₁₂Cu₁₂Sn₂₁ intermetallics^45–47 as well as A@B₁₂@A₂₀ (A = Sn, Pb; B = Mg, Zn, Cd, Mn) in cluster phase.⁴⁸ Unfortunately, their endohedral icosahedra commonly shares an empty or closed-shell d¹⁰ configuration, or d electrons are not taken into account for filling the superatomic orbitals. In this content, investigations should be done to explore whether above experience can be extended to other systems, in particular to a further suitable cluster/cage combination. What remained to be determined is which primary cage together with suitable encapsulation would be better for imparting novel superatoms. The dodecahedral Bi₂₀-fullercage⁴⁹ and icosahedral TM₁₃ clusters^50–56 have been previously determined to be very stable and low-lying energetically (not necessarily the lowest), and the isolate dodecahedral Bi₂₀-fullercage is the most stable one among nitrogen family of N, P, As, Sb cages.⁴⁹ Consequently, systemic encapsulations of TM₁₃ into Bi₂₀ would provide an opportunity to select a suitable elemental cluster in achieving the maximum strength of Bi–TM bond, because radii of core TM cluster is in progression from left to right for a row of the periodic table. Indeed, we have previously determined that for a given composition, the most favored structure of bimetallic BiMn and BiCo clusters tend to be an icosahedral TM₁₃-core encapsulated into a dodecahedral Bi-cage.⁵⁷ Such core–shell structure at high symmetry may offer the possibility of altering properties nearly at will by varying the number of itinerant electrons yet not breaking the electronic degeneracy.

With these views in mind, we perform a systematic density functional theory (DFT) investigations on the three-shell icosahedral matryoshka clusters [TM@TM₁₂@Bi₂₀]⁻, where TM atom encompasses every one of 3d and 4d periods. The key objective of current work is to explore the possibility of cluster being as superatom. What role, if any, does the electronic structure play? It further prompts the question, how general are the alignments of superatom orbitals in these clusters? For example, would they always hold true for different constituents regardless of the magnetic moment? The remaining of this paper is organized as follows: in Sec. II, we show the theoretical approach and computational details. The results are reported in Sec. III. Section IV contains a discussion and our conclusions.

2 Computational method

The representative structures of TM₁₃ and [TM₁₃@Bi₂₀]⁻ (TM = 3d, 4d) clusters are depicted in Fig. 1, where an icosahedral TM₁₃ fragment resides at the center of Bi₂₀ dodecahedral cage (fullerene) to give an onion-skin-like structure [TM@TM₁₂@Bi₂₀]⁻. Icosahedron TM₁₂ and pentagonal dodecahedron Bi₂₀ are reciprocal structures by switching their face-centers and vertexes,^45,58 i.e., each TM atom of the intermediate TM₁₂ shell is at the center of each Bi₅ ring of the outer Bi₂₀ shell and, in turn, each Bi atom is on the top of one TM₃ triangular face. Ultimately, 32 surface atoms form a dimpled geodesic sphere in I_h symmetry and it is composed of 60 triangular faces. The geometrical optimizations are performed at the constrained I_h symmetry and the initially imposed high spin moments. In an effort to confirm the magnetic ground state, allowing spin multiplicities are further examined on the optimal structure by alternating the values above and below the obtained spin multiplicity.

Fig. 1 Representative structure of TM₁₃⁻ cluster (a) and [TM₁₃@Bi₂₀]⁻ intermetalloid (b) in I_h symmetry.

The DFT optimizations are carried out by using the DMOL simulation package,⁵⁹ employing the effective core potential (ECP),^60,61 double-numerical basis sets with p-polarization function (DNP), and PW91 exchange–correlation potential under the generalized-gradient-approximation (GGA). The 3d4s, 4d5s, 6s6p electrons are respectively treated as the valence for 3d and 4d TM atoms and Bi atom, and relativistic effect at the scalar relativistic level is taken into account in the calculations. The direct inversion in iterative sub-space (DIIS) approach together with the thermal smearing scheme with a value of 0.005 Ha is adopted to speed up the self-consistent filed (SCF) convergence. The convergence criteria of 1 × 10⁻⁵ Ha Å⁻¹ for the energy gradient and 5 × 10⁻³ Å for the atomic displacement are forced in structural optimizations. The SCF charge density is converged to 1 × 10⁻⁶ e Å⁻¹, which allows a total energy convergence of 1 × 10⁻⁵ Ha. The density of states (DOS) was obtained by a Gaussian extension of the discrete energy levels and summation over them. The broadening width parameter was chosen to be 0.2 eV. The calculations of the atomic contributions to molecular orbitals of Sc₁₃@Bi₂₀ cluster to support the inspection of MO plots have been also performed with Gaussian 09 software at GGA/BPW91/6-311+G* level,⁶² and molecular orbitals visualization are performed by using the Molekel software.⁶³ The corresponding energy eigenvalues can be grouped into atomic-like shells (1S, 1P, 1D, 2S, 1F, 2P, …), depending on the degeneracy and spatial symmetry of the molecular orbitals. The lower case letters (s, p, d, …) are used to denote electronic levels in atoms and upper case letters (S, P, D, …) to denote the superatomic shells of electrons in a confined nearly-free electron gas.

3 Results and discussion

3.1 Stability analysis

For the endohedral [TM₁₃@Bi₂₀]⁻ clusters, we show in Table 1 the distances from central TM atom to intermediate TM atom (R_core) and to outer Bi atom (R_shell), binding energy (E_b), embedding energy (D_e), charge transfer (Q), HOMO–LUMO gap (gap), and electron affinity (EA). Corresponding values of anionic TM₁₃⁻ clusters are also presented as a reference. Thermal stability is estimated in terms of the binding energy E_b = (12E_TM + E_TM⁻¹ − E_cluster)/13 for anionic TM₁₃⁻ cluster and E_b = (12E_TM + E_TM⁻¹ + 20E_Bi − E_cluster)/33 for anionic [TM₁₃@Bi₂₀]⁻ cluster, where E_TM, E_TM⁻¹, and E_Bi are the energies of neutral TM, anionic TM, and neutral Bi atoms, respectively, and E_cluster is total energy of cluster. The embedding energy (D_e), defined as D_e = E_shell + E_core − E_endo, represents the gain in energy as TM₁₃⁻ cluster is encapsulated into Bi₂₀ cage, where E_shell, E_core, E_endo denote the optimal energies of Bi₂₀ cage, TM₁₃⁻¹ icosahedra, and endohedral [TM₁₃@Bi₂₀]⁻ system, respectively. For empty I_h-Bi₂₀ cage, our optimizations show that it has Bi–Bi bond-length of 3.04 Å and binding energy of 2.16 eV per atom, which agrees well with previous DFT values on the same structure.⁴⁹ For icosahedral TM₁₃⁻ clusters, the overall trends of binding energy as the function of element are consistent with the trends of previous works.^50–52,56

Table 1 Cage radii of core–shell R_core (Å) and outer-shell R_shell (Å), TM–Bi bond-length L (Å), binding energy E_b (eV per atom), embedding energy D_e (eV), charge transfer Q_atom, HOMO–LUMO gap (eV), electron affinity EA (eV), and magnetic moment M (μ_B) for [TM₁₃@Bi₂₀]⁻ and TM₁₃⁻ systems

TM13^−				[TM13@Bi20]^−
TM	R	Eb	Gap	Rcore	Rshell	L	Eb	De	QBi	QTM	QTM′	Gap	EA	M
Sc	3.03	2.80	0.32	3.09	4.94	3.10	3.20	26.02	−0.29	0.42	−0.25	0.21	3.33	0
Ti	2.63	3.67	0.97	2.76	4.70	3.01	3.66	29.80	−0.18	0.20	0.04	0.48	2.86	3
V	2.43	3.34	0.27	2.61	4.60	2.98	3.48	28.45	−0.13	0.16	−0.33	0.23	2.55	14
Cr	2.71	1.70	0.14	2.79	4.64	2.96	2.51	17.44	−0.17	0.21	−0.11	0.14	2.84	13
Mn	2.64	1.84	0.12	2.71	4.60	2.95	2.87	27.47	−0.11	0.11	−0.13	0.37	3.42	36
Fe	2.39	3.58	0.49	2.56	4.52	2.93	3.18	15.34	−0.13	0.03	1.32	0.25	2.73	33
Co	2.36	3.70	0.40	2.44	4.48	2.95	3.20	14.19	−0.07	0.04	−0.08	0.17	2.04	18
Ni	2.36	3.03	0.25	2.53	4.45	2.89	3.30	26.53	−0.13	0.13	0.07	0.12	2.85	5
Cu	2.46	2.15	0.73	2.55	4.52	2.94	2.49	10.93	−0.03	0.03	−0.09	0.98	1.71	4
Zn	3.01	0.66	1.99	2.78	4.73	3.03	1.50	−2.27	−0.10	0.10	−0.13	0.10	2.42	0
Y	3.33	3.04	0.04	3.42	5.19	3.23	3.32	26.82	−0.52	0.80	−0.19	0.21	3.92	0
Zr	2.91	4.66	1.28	3.07	4.90	3.12	4.09	31.30	−0.30	0.42	−0.02	0.64	3.02	3
Nb	2.77	4.65	0.38	2.93	4.76	3.01	4.02	29.12	−0.30	0.41	0.17	0.25	2.77	0
Mo	2.59	3.50	0.13	2.78	4.64	2.96	3.56	28.95	−0.21	0.24	0.33	0.12	2.51	7
Tc	2.52	4.26	0.26	2.68	4.58	2.94	3.89	29.66	−0.04	−0.04	0.17	0.16	2.30	4
Ru	2.54	4.28	0.14	2.77	4.53	2.87	4.19	39.38	0.04	−0.15	−0.01	0.17	2.18	11
Rh	2.58	3.79	0.11	2.90	4.54	2.85	3.02	7.11	0.05	−0.18	0.07	0.11	2.62	8
Pd	2.68	2.40	1.45	3.00	4.59	2.86	2.87	20.22	0.06	−0.18	−0.04	0.42	2.55	0
Ag	2.83	1.60	0.75	2.92	4.74	3.00	2.37	14.25	0.00	−0.06	−0.26	0.76	1.96	6
Cd	3.38	0.59	2.13	3.13	4.99	3.14	1.19	−11.64	−0.11	0.11	−0.23	0.16	2.58	5

---

In Fig. 2a and b, TM₁₃⁻ and [TM₁₃@Bi₂₀]⁻ clusters are compared to each other in E_b values as a function of constituent element. The analogous oscillation suggests that thermal stability of [TM₁₃@Bi₂₀]⁻ is primarily determined by TM₁₃ fragment but weakly effected by outer Bi₂₀ cage. On the one hand, two humps appear at Ti, Fe, Co, and Ni sites on E_b curve of [TM₁₃@Bi₂₀]⁻ clusters with TM = 3d series (Zr, Nb, and Ru sites for TM = 4d series), indicating that these doping counterparts are more thermally stable than others. Although there are a few relatively stable cases, most [TM₁₃@Bi₂₀]⁻ have the E_b over 3.0 eV (Table 1) that are generally large than the reported values of superatomic A@B₁₂@A₂₀ (A = Sn, Pb; B = Mg, Zn, Cd, Mn).⁴⁸ From a comparison of E_b values of [TM₁₃@Bi₂₀]⁻ between 3d and 4d counterparts given in Table 1 and shown in Fig. 2, the 3d doping ones often give smaller value than the 4d doping ones do for the early-half elements (i.e., from Sc to Fe for 3d series vs. from Y to Ru for 4d series), while it is substantially inverse for the late-half elements (i.e., from Co to Zn for 3d series vs. from Rh to Cd for 4d series). Even for the relatively large values at 3d elements of Ti (3.66 eV), Fe (3.18 eV), Co (3.20 eV), Ni (3.30 eV), they are still smaller than the relatively small values at 4d elements of Mo (3.56 eV) and Tc (3.89 eV). On the other hand, the positive D_e verifies the feasibilities that most TM₁₃⁻ species can be attractively embedded into Bi₂₀ cage (except for the negative values at Zn and Cd), and the large values at Ti, Fe, Mn, Ni for 3d series (Zr, Nb, and Ru for 4d series) reinforce the reliable assignment that they are more suitable in doping into Bi₂₀ cage to form stable [TM₁₃@Bi₂₀]⁻.

Fig. 2 The binding energy (a and b) and HOMO–LUMO gap (c and d) as a function of TM element.

The outer- and inner-cages with optimal matching size are crucial for designing a stable onion-skin-like structure, and thus it is indispensable to analyze their cage-radii. Between outer-Bi₂₀-shell and intermediate-TM₁₂-icosahedra, the bond-lengths of Bi–TM range from 2.85 Å to 3.23 Å, which are somewhat longer than the typical values of bimetallic dimers. In fact, strong interactions between TM and Bi atoms can be discerned by the contractive distance between outer-shell and intermediate-shell: before doping, R_outer between centroid-site and surface Bi is 4.26 Å for Bi₂₀ cage (R_core ranges from 2.36 Å to 3.38 Å for TM₁₃⁻); after doping, R_outer and R_core are respectively elongated to 4.45–5.19 Å and 2.44–3.42 Å for endohedral [TM₁₃@Bi₂₀]⁻. By calculating the elongated differences in radii (Δ²R = ΔR_shell − ΔR_core), one can estimate the magnitude of their interactions because small Δ²R is related to short TM–Bi bond-length. The variations of Δ²R along the elemental atoms are plotted in Fig. 3, where small values are at middle period. This can be related to that more d electrons take part in chemical bonds to strengthen TM–Bi bond-length. In addition, Δ²R present a similar trend for 3d and 4d period owing to an analogous evolution of electronic configurations.

Fig. 3 The difference of the elongated radii Δ²R = ΔR_shell − ΔR_core.

The chemical stabilities of [TM₁₃@Bi₂₀]⁻ are examined via the energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). The HOMO–LUMO gaps for 3d (4d) doping series are plotted in Fig. 2c (2d), where the values at Ti, Mn, and Cu for 3d elements (Zr and Ag for 4d elements) are remarkably larger than that at others. The superior chemical stability of these systems can be related to the contributions of electronic structure since their structural configurations are same. Interestingly, TM₁₃⁻ and [TM₁₃@Bi₂₀]⁻ generally exhibit a comparable value of HOMO–LUMO gap, indicating the prominent role of TM₁₃⁻ in determinations of electronic structure. For TM = nd¹⁰ elements, TM₁₃⁻ are found to be an insulator (gaps are 1.99 eV and 2.13 eV for Zn₁₃⁻ and Cd₁₃⁻) while [TM₁₃@Bi₂₀]⁻ counterparts are almost a metal (corresponding values decrease to 0.10 eV and 0.16 eV). The is attributed to the hybridization effect between sp states of TM atoms and 6p states of Bi atoms, e.g., the HOMO-level of Cd₁₃⁻ cluster (5s states) is lower in energy than the HOMO-level of Bi₂₀ cage (6p state), but an opposite case is found for the LUMO-level (5p state at high level for Cd₁₃⁻ vs. 6p states at low level for Bi₂₀). Once Cd₁₃⁻ is doped into Bi₂₀ cage, 6p electrons from HOMO state of Bi₂₀ would form a new occupied-orbital (being as the HOMO of [TM₁₃@Bi₂₀]⁻) and LUMO state of Bi₂₀ would form a new unoccupied-orbital (being as the LUMO of [TM₁₃@Bi₂₀]⁻), resulting in the decreased gap from 2.13 eV for Cd₁₃⁻ to 0.16 eV for [Cd₁₃@Bi₂₀]⁻. The HOMO and LUMO of [Cd₁₃@Bi₂₀]⁻ are mostly contributed from Bi-6p states can be evidenced by their electron density, i.e., it is found that the accumulated charges are mainly around the Bi atom in [TM₁₃@Bi₂₀]⁻. Further verifying of gaps via the partial DOS will be discussed in the following section, where the HOMO and LUMO of [Sc₁₃@Bi₂₀]⁻ mainly consist of 6p orbitals of Bi atoms.

The moderate gaps 0.37–0.98 eV are presented by [TM₁₃@Bi₂₀]⁻ (TM = Ti, Mn, Cu, Zr, Ag) clusters, which are much smaller than the values of previously proposed nonmagnetic superatoms, i.e., [As@Ni₁₂@As₂₀]⁻³ (1.46 eV),^45,46 [Sn@Cu₁₂@Sn₂₀]⁻¹² (1.34 eV),⁴⁷ and A@B₁₂@A₂₀ (A = Sn, Pb; B = Mg, Zn, Cd) (1.27–1.54 eV).⁴⁸ One thing should be emphasized here that, atoms within empty or closed-shell d¹⁰ configuration have been merely considered in previous works (d electrons are not taken into account for filling the superatomic orbitals). Since the energy gaps between adjacent energy levels decrease continuously with the increase of quantum numbers, it is no surprise that [TM₁₃@Bi₂₀]⁻ systems having more valence electrons (fill to the superatomic orbitals with high quantum numbers) would present somewhat small HOMO–LUMO gaps with respect to that of the systems having less valence electrons (fill to the superatomic orbitals with low quantum numbers). In addition, there is a strong tendency that the standard GGA and LDA approximations to DFT often underestimate the gaps while hybrid functionals such as PBE0,^64,65 HSE06,⁶⁶ and B3LYP⁴⁷ will predict slightly more accurately. This may also be the reason we obtained smaller gaps at standard GGA level. Nevertheless, if the energy gaps of the previously proposed magnetic superatoms are taken as the references, our moderate values of specific magnetic clusters are always comparable to their reports, i.e., V@Na₈ (0.42 eV),²⁶ Sc@K₁₂ and Sc@Cs₁₂ (0.35 eV),²⁹ Fe@Ca₈ (0.61 eV),³⁰ Fe@Mg₈ (0.64 eV),³² Tc@Mg₈ (0.65 eV),³³ Mn@Ca₉ (0.92 eV),³⁴ Mn@Sr₉ (0.39 eV)³⁶ as well as the analogous structures of [Pb@Mn₁₂@Pb₂₀] (0.61 eV) and [Sn@Mn₁₂@Sn₂₀] (0.38 eV).⁴⁸

3.2 Electron filling rule

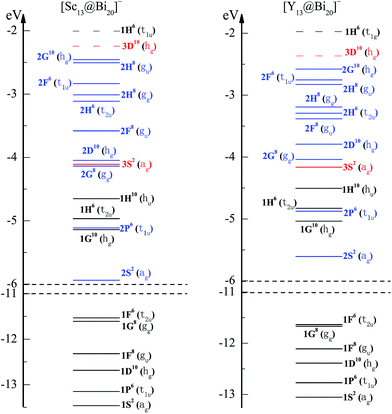
For an ideal spherical structure like a free atom, its highly degenerate atomic orbitals would resemble the spherical harmonics and could be identified with spherical electronic shells (1S²1P⁶1D¹⁰2S²1F¹⁴2P⁶1G¹⁸2D¹⁰3S²1H²²2F¹⁴3P⁶1I²⁴2G¹⁸…, or alternation of the sequence of electronic shells); however, for a nearly spherical structure like an icosahedron, the degeneracy in some electronic states will be broken by the rearrangement of internal ionic forming synthetic cluster. Owning to icosahedral ligand field of [TM₁₃@Bi₂₀]⁻ structure (the highest symmetry axis is in 5-fold), the molecular orbitals within a high angular momentum that is more than 5-fold degenerate (labeled by F, G, H…) will split into a set of sub-orbitals. According to the irreducible representations of point group I_h symmetry, generally speaking, S-type orbitals show a_g symmetry, P-type orbitals show as t_1u symmetry, D-type orbitals transform as h_g, F-type orbitals split into two sets transforming as g_u + t_2u or g_u + t_1u, G-type orbitals split into two sets of g_g + h_g symmetry, and H-type orbitals split into three sets of t_2u + g_g + g_u or t_2u + t_1u + h_u symmetry.⁴⁷

In an effort to evaluate the superatomic characteristics of a series of [TM₁₃@Bi₂₀]⁻ clusters, [Sc₁₃@Bi₂₀]⁻ cluster is firstly exemplified to illustrate the filling rule of valence electrons into each molecular orbital in the consideration of its total 140 valence electrons. Free Bi and Sc atoms are in the configuration 6s²6p³ and 3d¹4s², and Bi₂₀ and Sc₁₃ fragments would provide 100 and 39 valence electrons to valence pool, respectively. Charge density isosurfaces and one-electron energy levels for the Kohn–Sham molecular orbitals of [Sc₁₃@Bi₂₀]⁻ cluster are presented in Fig. 4 and 5, respectively, where each molecular orbital is distinguishingly assigned by the inspection of their nodes, shapes, and energetic sequence analogous to that of atomic orbitals. From Fig. 4, one can note that the spatial shapes of each molecular orbital resemble the corresponding atomic orbital, e.g., the lowest energy state is spread out over the entire cluster accommodating 2 electrons, and thus it can be regarded as the 1S superorbital. Except for the low-lying states from 1S to 1F that are fairly diffused over Bi outer-shell and can be deemed to be the contributions of Bi-6s electrons, other states have the large amplitudes on both Bi and TM sites, indicating the strong hybridizations between Bi-6p states and TM-3d states. In addition, the molecular orbitals within high angular momentum come to split into a set of suborbitals as analyzed above. In brief, the filling of 70 superatomic orbitals is proposed to in energy sequence of 1S²(a_g)1P⁶(t_1u)1D¹⁰(h_g)1F⁸(g_u)1G⁸(g_g) 1F⁶(t_2u)2S²(a_g)1G¹⁰(h_g)2P⁶(t_1u)1H⁶(t_2u)1H¹⁰(h_u)2G⁸(g_g)3S²(a_g)2D¹⁰(h_g)2F⁸(g_u)2H⁶(t_2u)2H⁸(g_g)2F⁶(t_1u)2H⁸(g_u)2G¹⁰(h_g). Nevertheless, it has been proposed that D supershell is followed by F supershell in a homogeneous confined nearly free electron gas (jellium model for a homogeneous cluster); it however leads to 2G over 2D and 2F set of orbitals in bimetallic heterogeneous clusters.

Fig. 4 The molecular orbital charge density isosurfaces (iso = 0.001 a.u. for 1S, 2S and 3S orbitals; 0.002 a.u. for 1P, 1D, 1F, 2P, 2D, 2F and 3D orbitals; 0.02 a.u. for the 1H, 2H, 1G and 2G orbitals) for [Sc₁₃@Bi₂₀]⁻.

Fig. 5 The energy levels (in eV) of molecular orbitals of [Sc₁₃@Bi₂₀]⁻ and [Y₁₃@Bi₂₀]⁻, which are assigned to a series of superatomic orbitals corresponding to the indicated spherical harmonics. Continuous lines correspond to the occupied levels, whereas the broken lines correspond to the unoccupied states. For each level, the angular character (with upper-case letter), total electrons (with superscript), and degenerated states (within parenthesis) are marked.

In Fig. 5, the first shell n = 1 of the occupation 1S²1P⁶1D¹⁰1F¹⁴1G¹⁸1H¹⁶ shows an incompletely filled 1H orbitals (fully filled 1H sub-shell needs 22 electrons): 1H molecular orbitals split into one 5-fold degenerate sub-orbitals and two 3-fold degenerate sub-orbitals; the 5-fold degenerate sub-orbitals 1H¹⁰(h_u) and the low-lying 3-fold degenerate sub-orbitals 1H⁶(t_2u) are fully occupied by 16 electrons while the high-lying 3-fold degenerate sub-orbitals 1H⁶(t_2u) are above the Fermi level and empty. Except for 1G⁸(g_g) and 1F⁶(t_2u) orbitals that are almost equal in energy, the orbital sets of Bi-6s block (1S⋯1F orbitals) are energetically well separated from each other. The second shell n = 2 of the occupation 2S²2P⁶2D¹⁰2F¹⁴2G¹⁸2H²² as well as the third shell n = 3 of the occupation 3S², show both closure sub-shell configurations. There is a modest energy separation of 0.21 eV between the HOMO of 2G¹⁰(h_g) and LUMO of 3D¹⁰(h_g). This filling configuration is reminiscent of atomic situation in Mg atom ([Ne]3s²). By comparing the electronic shells of [Y₁₃@Bi₂₀]⁻ with its iso(valence) electronic counterpart of [Sc₁₃@Bi₂₀]⁻, one found that the molecular orbitals of [Y₁₃@Bi₂₀]⁻ are arranged in analogy to those of [Sc₁₃@Bi₂₀]⁻ with two exceptions that the energy orders of 2G⁸(g_g) ⇌ 3S²(a_g) orbitals as well as 2F⁶(t_1u) ⇌ 2H⁸(g_u) orbitals are alternated. Generally speaking, quantum states of these two clusters can be bunched into supershells with associated orbitals having the shapes resembling those in atoms, and they can be classified as superatoms.

Fig. 6 shows the partial density of states (PDOS) projected at Sc and Bi sites of [Sc₁₃@Bi₂₀]⁻. Below the energy level −11.0 eV, 20 lowest-lying orbitals of 1S²1P⁶1D¹⁰1F¹⁴1G⁸ are primarily accommodated by 2 × 20 = 40 6s valence electrons from Bi₂₀ skeleton frame. This is consistent with previous findings that for a polyhedral cluster with structure vertices occupied by “p-block” element atoms, their lowest-lying “S-block” molecular orbitals mainly comprise atomic s orbitals of “p-block” element atoms.^47,67,68 In the combination of Fig. 5 and 6, it is clear that the following orbitals are dominated by the contributions of Bi-6p, Sc-4s, Sc-3d electrons (3 × 20 + 3 × 13 + 1 = 100): 2S² orbital at −6.0 eV is filled by Sc-4s states with Bi-6p characters admixing (2 electrons); 1G¹⁰2P⁶1H⁶ orbitals around −5.0 eV and 2G⁸3S²2D¹⁰ orbitals around −4.0 eV have contributions from Bi-6p states mixing with Sc-4s and Sc-3d states (42 electrons); 2F⁸ orbitals at −3.5 eV are merely composed of Bi-6p states (8 electrons); the remaining orbitals 1H¹⁰2H⁸2H⁶2F⁶2H⁸2G¹⁰ (48 electrons) are basically from Bi-6p and Sc-3d states in strong hybridizations. On the whole, PDOS ranging from −6.0 to −2.0 eV show a high share of Bi-6p contributions, and the occupied electrons may be described as the Bi–Bi surface bonding in main.

Fig. 6 Spin-polarized partial density of states (PDOS) for [Sc₁₃@Bi₂₀]⁻. The HOMO level is marked by the dotted line.

Previously, electronic account scheme on [As@Ni₁₂@As₂₀]³⁻ has been proposed by Moses and Zhao et al.,^45,46 i.e., 60 of 100 valence electrons of As₂₀ pentagonal dodecahedron are involved in 30 As–As bonds along 30 edges, and the remaining 40 are attributed to 20 As-p_z orbitals oriented radially with respect to cluster surface and termed as ąřp_z lone-pair electronsąś. They have also determined somewhat radial interactions between 20 As-p_z orbitals of As₂₀ and virtual orbitals of As@Ni₁₂, together with the negligible interactions between 30 As–As bonding orbitals of As₂₀ and Ni–Ni bonding orbitals of As@Ni₁₂. In terms of above electronic account scheme, on the one hand, if 40 6s-electrons of outer Bi₂₀ are regarded as p_z-like lone-pair electrons (60 6p-electrons are as Bi–Bi bonding electrons), the 6s states of outer Bi₂₀ cage should interact with s and d states of inner Sc₁₃ fragment. However, from the PDOS of [Sc₁₃@Bi₂₀]⁻ in Fig. 6, no hybridization between Bi-6s and Sc-3d, 4s is discerned. On the other hand, if 40 6p-electrons of outer Bi₂₀ are regarded as the p_z lone-pair electrons, then the residual 20 6p-electrons together with 40 electrons from Bi-6s states are involved in forming Bi–Bi bonds. Unexpectedly, 40 6s-electrons do not participate in Bi–Bi or Bi–Sc bonds from the PDOS. As a matter of fact, our previous DFT calculations on Bi clusters⁶⁹ have revealed that the average Mayer bond-orders between Bi atoms decrease from 3 in Bi₂ dimer to 1 in Bi₄ tetrahedral and to 0.89 in Bi₂₄ chain-like cluster (average coordination number increases from 1 to 3 and to 3.05), suggesting that three 6p electrons of each Bi atom are merely being ready to form chemical bonds while two 6s electrons are being as lone pairs. In addition, DFT investigations on BiMn clusters also determined no hybridization between Bi-6s states and Mn-3d, 4s, 4p states.⁵⁷ Therefore, above electronic account scheme is not applicable for [Sc₁₃@Bi₂₀]⁻ cluster and for Bi-based relevant [TM₁₃@Bi₂₀]⁻ clusters.

In addition, considerable elongations of Bi–Bi bond-length in [TM₁₃@Bi₂₀]⁻ clusters require less 6p-electrons to form weak Bi–Bi bonds, and more remaining 6p-electrons would exist as the lone pairs in p_z orbitals (i.e., less than 60 6p-electrons are required to form 30 dodecahedral Bi–Bi edges, and then more remaining 6p-electrons are as lone-pair electrons to form Bi–TM bonds.) Our calculations on the Mayer bond-orders of [TM₁₃@Bi₂₀]⁻ clusters show that the bond-orders between the nearest neighbor Bi atoms range from 0.32 to 0.38, indicating that nearly one electrons of each Bi atom would take part in the formation of three Bi–Bi bonds. Consequently, 20 6p-electrons of Bi₂₀ are indeed as Bi–Bi bonding electrons and 40 6p-electrons are as p_z lone-pair electrons to form Bi–TM bonds. This partitioning scheme of Bi₂₀ electrons is in agreement with the population analyses. According to on-site population analysis (by Mulliken definition), TM-atoms of intermediate shell often partially donate their s electrons to Bi-atom 6p and 6d orbitals, while most centered TM-atom d and p orbitals gains electrons. The situations come to reverse for Ru, Rh, Pd, Ag dopants, where Bi-atoms donate their electrons to outer-TM₁₂ and inner-TM atoms (Table 1). The charge transferring indicates the occurrence of hybridizations between Bi-p, TM-s, p, and d states, and thus all clusters share the same pattern of chemical bonding. However, no matter what kind of situations, the numbers of Bi-atom 6s electrons always maintain the same, suggesting no interactions between Bi-atom 6s state and other states.

3.3 Magnetic analysis

Superatomic cluster is remarkably stable because of its filling electronic shells with paired electrons, corresponding to a nonmagnetic state such as nonmagnetic [Sc₁₃@Bi₂₀]⁻ cluster. Here, we will focus on Mn₁₃ endohedral [Mn₁₃@Bi₂₀]⁻ cluster, based on the magnetic fact that [Mn₁₃@Au₂₀]⁻, [Pb@Mn₁₂@Pb₂₀], and [Sn@Mn₁₂@Sn₂₀] were predicted to possess giant magnetic moments of 44, 28, and 28 μ_B,^48,70 respectively. Previously, magnetic superatoms can be achieved by doping a singly magnetic TM atom into a small simple-metal cluster, because either superatomic D-state has strong component from atomic d-state (i.e., d electrons are regarded as the delocalized valences in filling superatomic shells) or superatomic D-state hybridize strongly with d-states (i.e., d electrons are regarded as the localized valences and do not fill superatomic shells).^26–36 Above both cases can result in the exchange-splitting between the majority and minority states either of superatomic D shells or of atomic d shells, leading to a superatom with a spin magnetic moment. Unfortunately, the maximum magnetic moments in these systems are often less than 6 μ_B, since the numbers of their valence electrons are not enough to fill superatomic shells large than nD (the largest spin moment is 5 μ_B when the degenerated 1D orbital is half-filled). Even if some systems can provide enough valence electrons to fill superatomic shells with large orbital quantum numbers, owning to the potential field splitting of ionic cores of their oblate shape, they would break the degeneracy of orbitals into several groups of sub-orbitals. This would lower the prospective magnetic moments further. One may question whether or not above deficiency could be overcome by a large cluster with an utmost spherical configuration. Consequently, iso-structures of [Mn₁₃@Bi₂₀]⁻ is quite intriguing to represent a distinct magnetic moment among 3d and 4d doping series (Table 1). It should be mentioned again that the geometrical optimizations are first done by ferromagnetically imposing maximum spin moment on each TM atom in terms of Hund's first rule so as to search for the structural minima, and then the energy minimizations for a number of fixed total spin moments are orderly executed by alternating the spin moments above and below the obtained value in first step. If the total energy decreases with the variations of total spin moments of cluster, further spin state will be considered until the energy minimum with respect to ground spin state is reached. In addition, for clusters having sizeable spin values in first optimization step, various spin arrangements are also tried in a quest for the spin ground state.

Fig. 7 presents the PDOS and spin density distribution, which is associated with each orbital level for [Mn@Mn₁₂@Bi₂₀]⁻. As demonstrated by the spin density distribution in Fig. 7, the magnetism mainly localizes on Mn atoms. By analyzing the PDOS in addition, three interesting things can be discerned: (1) the alignment of superatomic orbitals of magnetic [Mn₁₃@Bi₂₀]⁻ still resembles those of non-magnetic [Sc₁₃@Bi₂₀]⁻, supporting the universal filling principle of valence electrons into superatomic shell for different [TM₁₃@Bi₂₀]⁻; (2) 3F, 3G, 3H, 4S, 4P, 4D superatomic states are dominantly from the contributions of Mn-3d states and Bi-6p states; (3) large exchange-splitting between the majority and minority superatomic states happens to occur, coincidentally with large exchange-splitting of Mn-3d states. For example, the majority 3F⋯4D sub-shells are fully filled while the corresponding minority counterparts are fully empty. In addition, Mulliken population analysis shows again that 3F⋯4D states have large contribution from the Mn-d states, i.e., magnetic moment is mainly localized on Mn atom (3.82 μ_B per Mn atom of intermediate Mn shell; −4.22 μ_B of central Mn), and a small amount of antiferromagnetic moment is found on outer Bi atoms (−0.28 μ_B per Bi atom). Therefore, one can reasonably deduce that the splitting in Mn-3d state is the driving force for the splitting of supershells. The full-filled shells within 156 electrons (1S²1P⁶1D¹⁰1F¹⁴1G¹⁸1H¹⁶‖2S²2P⁶2D¹⁰2F¹⁴2G¹⁸2H²²‖3S²3P⁶3D¹⁰), together with the half-filled majority orbitals within 36 alpha electrons (3F⁷_α3G⁹_α3H¹¹_α‖4S¹_α4P³_α4D⁵_α) and the full-empty corresponding minority orbitals, lead to [Mn₁₃@Bi₂₀]⁻ a stable species having a moderate HOMO–LUMO gap of 0.37 eV. The majority 3F⋯4D superatomic states of [Mn₁₃@Bi₂₀]⁻ give a giant total magnetic moment of 7 + 9 + 11 + 1 + 3 + 5 = 36 μ_B. This exemplifying study on magnetic [Mn₁₃@Bi₂₀]⁻ reinforces our finding that the filling of superatomic shells is also appreciate for magnetic [TM₁₃@Bi₂₀]⁻ species, and it can be classified as magnetic superatoms.

Fig. 7 The occupied superatom orbitals are labeled on the spin-polarized density of states (DOS) for [Mn₁₃@Bi₂₀]⁻, where the d states from Mn atoms are filled by green color. The isosurface of spin density distribution is presented (blue areas) as insert chart.

The [Fe₁₃@Bi₂₀]⁻ has 13 more addition valence electrons compared to [Mn₁₃@Bi₂₀]⁻, for which 5 of 13 electrons would like to fill into one of the splitted majority sub-orbitals 4G_α5↑ (4G_α9 → 4G_α5 + 4G_α4) while the remaining 8 electrons would like to fill into the minority orbitals 4S_β1 4P_β3 3G_β4. This results in a closed-shell configuration within 164 valence electrons (1S²1P⁶1D¹⁰1F¹⁴1G¹⁸1H¹⁶‖2S²2P⁶2D¹⁰2F¹⁴2G¹⁸2H²²‖3S²3P⁶3D¹⁰4S²4P⁶) and the opened-shell configuration having 37 alpha and 4 beta electrons (3F_α73G_α93H_α11‖4D_α54G_α53G_β4). Consequently, [Fe₁₃@Bi₂₀]⁻ has total valence electrons of 205 and magnetic moment of 33 μ_B. For [Co₁₃@Bi₂₀]⁻ within additional 26 electrons compared to [Mn₁₃@Bi₂₀]⁻ (218 total valence electrons), 4 electrons fill into the majority subshell 4G_α4 to form a configuration of 3F_α73G_α93H_α11‖4S_α14P_α34D_α54G_α4, and 22 valence electrons fill into the minority subshell 3F_β73G_β53H_β6‖4S_β14P_β3 (3G_β9 → 3G_β5 + 3G_β4; 3H_β11 → 3H_β3 + 3H_β3 + 3H_β5), resulting in a magnetic moment of 18 μ_B. Nevertheless, the partially filled sub-shells lead to somewhat small gaps of 0.25 eV and 0.17 eV for [Fe₁₃@Bi₂₀]⁻ and [Co₁₃@Bi₂₀]⁻, respectively. From the Table 1, as we go across the 3d period series after Mn element, more additional electrons would like to occupy the minority orbitals than the majority orbitals, giving rise to decreasing numbers of unpaired electrons and thus the decreasing magnetic moments along elemental table. Strangely, although Cu₁₃, Ag₁₃ and Cd₁₃ are nonmagnetic species, [TM₁₃@Bi₂₀]⁻ can present modest magnetic moments of 4 μ_B, 6 μ_B and 5 μ_B at Cu, Ag and Cd cases, respectively. This means that even if there is no driving force from magnetic TM₁₃ to induce magnetism on [TM₁₃@Bi₂₀]⁻, superatoms can also yield magnetic moment through the exchange splitting between the majority and minority states of superatomic orbitals. Therefore, this work offers two strategies to design magnetic superatom by the improvement of exchange splitting between majority and minority superatomic states: one is by magnetic TM₁₃ fragment inducement; another one is originated from the partial fillings of superatomic shells to result in unpaired electrons following Hund's rule.

4 Conclusion

To develop the novel superatoms, a systemic study of structural, electronic, and magnetic properties of icosahedra TM₁₃⁻ (TM = 3d, 4d) clusters encapsulated into pentagonal dodecahedra Bi₂₀ cage has been performed by using the DFT method. Unlike the cases in previous works, here, we design a framework by invoking systems that take d electronic states as valence electrons to fill the superatomic orbital states. The stability of [TM₁₃@Bi₂₀]⁻ cluster is analyzed in terms of binding energy, embedding energy, and HOMO–LUMO gap, and the results show that most TM₁₃⁻ species can be attractively embedded into Bi₂₀ cage to form a stable three-shell icosahedral matryoshka cluster. Following the definition of superatom of jellium model, we propose that [TM₁₃@Bi₂₀]⁻ clusters can mimic the atomic patterns in electronic shells in both molecular diagrams and energy consequences, and they share an analogy behavior of superatomic orbitals. It is determined that the partial d electrons bring the magnetic moments by improving the exchange-splitting of superatomic orbitals of high angular momentum, while the remaining d electrons together with s, p electrons contribute to the stability by filling the superatomic orbitals to form the full-filled or half-filled subshells. Stable [Mn₁₃@Bi₂₀]⁻ cluster is predicted to exhibit large magnetic moment (36 μ_B) and moderate HOMO–LUMO gap owning to its half-filled superatomic subshell, and thus it is being as a protyle magnetic superatom.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Project No. 10904125 and 91121013), the National College Students' Innovation and Entrepreneurship Training Program (Project No. 20130635060), and the Fundamental Research Funds for the Central Universities (Project No. XDJK2012B008).

References

1. M. Brack, Rev. Mod. Phys., 1993, 65, 677–732.
2. W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611–676.
3. W. D. Knight, K. Clemenger, W. A. de Heer Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143.
4. S. N. Khanna and P. Jena, Phys. Rev. Lett., 1992, 69, 1664–1667.
5. S. N. Khanna and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13705–13716.
6. A. W. Castleman Jr and S. N. Khanna, J. Phys. Chem. C, 2009, 113, 2664–2675.
7. A. W. Castleman Jr, S. N. Khanna, A. Sen, A. C. Reber, M. Qian, K. M. Davis, S. J. Peppernick, A. Ugrinov and M. D. Merritt, Nano Lett., 2007, 7, 2734–2741.
8. C. Ashman, S. N. Khanna, F. Liu, P. Jena, T. Kaplan and M. Mostoller, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15868–15875.
9. C. Y. Cha, G. Ganteför and W. Eberhardt, J. Chem. Phys., 1994, 100, 995–1010.
10. R. E. Leuchtner, A. C. Harms and A. W. Castleman Jr, J. Chem. Phys., 1989, 91(4), 2753–2754.
11. D. E. Bergeron, A. W. Castleman Jr, T. Morisato and S. N. Khanna, Science, 2004, 304, 84–87.
12. X. Li, H. Wu, X. B. Wang and L. S. Wang, Phys. Rev. Lett., 1998, 81, 1909.
13. D. E. Bergeron, P. J. Roach, A. W. Castleman Jr, N. O. Jones and S. N. Khanna, Science, 2005, 307, 231–235.
14. J. U. Reveles, S. N. Khanna, P. J. Roach and A. W. Castleman Jr, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18405–18410.
15. M. Akutsu, K. Koyasu, J. Atobe, N. Hosoya, K. Miyajima, M. Mitsui and A. Nakajima, J. Phys. Chem. A, 2006, 110, 12073–12076.
16. P. A. Clayborne, O. Lopez-Acevedo, R. L. Whetten, H. Grönbeck and H. Häkkinen, J. Chem. Phys., 2011, 135, 094701.
17. O. Lopez-Acevedo, P. A. Clayborne and H. Häkkinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035434.
18. P. Pyykkö and N. Runeberg, Angew. Chem., 2002, 114, 2278–2280.
19. P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430–433.
20. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162.
21. M. Zhu, C. M. Aikens, M. P. Hendrich, R. Gupta, H. Qian, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2009, 131, 2490–2492.
22. J. Nishigaki, K. Koyasu and T. Tsukuda, Chem. Rec., 2014, 14, 897–909.
23. M. Walter and H. Häkkinen, Phys. Chem. Chem. Phys., 2006, 8, 5407–5411.
24. S. N. Khanna, B. K. Rao, P. Jena and J. L. Martins, Physics and Chemistry of Small Clusters, ed. P. Jena, B. K. Rao and S. N Khanna, Plenum Press, New York, 1987, pp. 435–438.
25. M. Zhang, J. Zhang, X. Feng, H. Zhang, L. Zhao, Y. Luo and W. Cao, J. Phys. Chem. A, 2013, 117, 13025–13036.
26. X. Zhang, Y. Wang, H. Wang, A. Lim, G. Gantefoer, K. H. Bowen, J. U. Reveles and S. N. Khanna, J. Am. Chem. Soc., 2013, 135, 4856–4861.
27. J. U. Reveles, P. A. Clayborne, A. C. Reber, S. N. Khanna, K. Pradhan, P. Sen and M. R. Pederson, Nat. Chem., 2009, 1, 310–315.
28. J. U. Reveles, P. Sen, K. Pradhan, D. R. Roy and S. N. Khanna, J. Phys. Chem. C, 2010, 114, 10739–10744.
29. K. Pradhan, J. U. Reveles, P. Sen and S. N. Khanna, J. Chem. Phys., 2010, 132, 124302.
30. V. Chauhan, V. M. Medel, J. U. Reveles, S. N. Khanna and P. Sen, Chem. Phys. Lett., 2012, 528, 39.
31. V. M. Medel, A. C. Reber, J. U. Reveles and S. N. Khanna, J. Chem. Phys., 2012, 136, 134311.
32. V. M. Medel, J. U. Reveles, S. N. Khanna, V. Chauhan, P. Sen and A. W. Castleman, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10062–10066.
33. G. X. Ge, Y. Han, J. G. Wan, J. J. Zhao and G. H. Wang, J. Chem. Phys., 2013, 139, 174309.
34. V. M. Medel, J. U. Reveles, M. F. Islam and S. N. Khanna, J. Phys. Chem. A, 2013, 117, 4297–4303.
35. V. Chauhan and P. Sen, Chem. Phys., 2013, 417, 37–44.
36. V. M. Medel, J. U. Reveles and S. N. Khanna, J. Appl. Phys., 2012, 112, 064313.
37. J. Hartig, A. Stösser, P. Hauser and H. Schnöckel, Angew. Chem., Int. Ed., 2007, 46, 1658–1662.
38. H. Cantera-López, L. C. Balbás and G. Borstel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075434.
39. A. K. Singh, V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115429.
40. V. Kumar and Y. Kawazoe, Appl. Phys. Lett., 2003, 83, 2677–2679.
41. V. Kumar and Y. Kawazoe, Appl. Phys. Lett., 2002, 80, 859–861.
42. S. Neukermans, E. Janssens, Z. F. Chen, R. E. Silverans, P. V. R. Schleyer and P. Lievens, Phys. Rev. Lett., 2004, 92, 163401.
43. B. Zhou, T. Krämer, A. L. Thompson, J. E. McGrady and J. M. Goicoechea, Inorg. Chem., 2011, 50, 8028–8037.
44. L. Cheng and J. Yang, J. Chem. Phys., 2013, 138, 141101.
45. M. J. Moses, J. C. Fettinger and B. W. Eichhorn, Science, 2003, 300, 778–780.
46. R. B. King and J. Zhao, Chem. Commun., 2006, 4204–4205.
47. S. Stegmaier and T. F. Fässler, J. Am. Chem. Soc., 2011, 133, 19758–19768.
48. X. Huang, J. Zhao, Y. Su, Z. Chen and R. B. King, Sci. Rep., 2014, 4, 6915.
49. A. D. Zdetsis, J. Phys. Chem. C, 2010, 114, 10775–10781.
50. Y. Sun, M. Zhang and R. Fournier, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075435.
51. Y. Sun, R. Fournier and M. Zhang, Phys. Rev. A, 2009, 79, 043202.
52. M. Zhang and R. Fournier, Phys. Rev. A, 2009, 79, 043203.
53. H. K. Yuan, H. Chen, A. L. Kuang, C. L. Tian and J. Z. Wang, J. Chem. Phys., 2013, 139, 034314.
54. H. K. Yuan, H. Chen, A. L. Kuang, A. S. Ahmed and Z. H. Xiong, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 174412.
55. H. K. Yuan, H. Chen, A. S. Ahmed and J. F. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 144434.
56. M. J. Piotrowski, P. Piquini and J. L. F. Da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155446.
57. H. Chen, H. K. Yuan, A. L. Kuang, Y. Miao, P. Chen and Z. H. Xiong, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184429.
58. G. Bergman, J. L. Waugh and L. Pauling, Acta Crystallogr., 1957, 10, 254–259.
59. DMOL, V960, Biosym Technologies, San Diego, CA, 1996.
60. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
61. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
62. M. J. Frisch, Gaussian 09, revision B.01, Gaussian, Inc., Wallingford, CT, 2010.
63. U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Centre, Manno, Switzerland, 2009.
64. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
65. P. Liu, J. Nisar, R. Ahuja and B. Pathak, J. Phys. Chem. C, 2013, 117, 5043–5050.
66. P. Liu, J. Nisar, B. Pathak and R. Ahujaab, Phys. Chem. Chem. Phys., 2013, 15, 17150–17157.
67. S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fäsler, Angew. Chem., Int. Ed., 2011, 123, 3712–3754.
68. B. Wahl, M. Erbe, A. Gerisch, L. Kloo and M. Ruck, Z. Anorg. Allg. Chem., 2009, 635, 743–752.
69. H. K. Yuan, H. Chen, A. L. Kuang, Y. Miao and Z. H. Xiong, J. Chem. Phys., 2008, 128, 094305.
70. J. Wang, J. Bai, J. Jellinek and X. C. Zeng, J. Am. Chem. Soc., 2007, 129, 4110–4111.

---