Why do the structural properties of complexes formed by glucans and carbon nanotubes differ so much?

Abstract

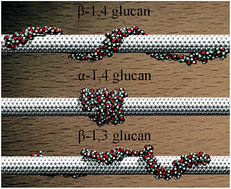
In supramolecular wrapping chemistry, polysaccharides are widely used as wrapping agents for the dissolution, dispersion and functionalization of carbon nanotubes. It is, therefore, of paramount importance to understand the effect of the topology – specifically the linkage – of the polymer chain on its spatial arrangement around the hollow tubular structure, and, hence, on the configuration and the nature of the supramolecular complex. To this end, the β-1,4, α-1,4 and β-1,3-glucans were chosen to wrap a single-walled carbon nanotube (SWCNT) as three prototypical assemblies. Molecular simulations reveal that α-1,4-glucan has the ability to wrap SWCNTs very tightly, whereas β-1,3-glucans can only form irregular helices. The calculated binding affinity of the polysaccharide to the tubular surface follows the order α-1,4 > β-1,4 > β-1,3-glucan. The differences between the three hybrids can be generally described in terms of the inherent propensity of glucans to fold into helices, the hydrophobic interaction of the polysaccharide with the SWCNT, and the formation of intramolecular hydrogen bonds within the polymer chain. The wrapping mode of the glucan chain is mainly determined by its inherent helicity. The hydrophobic interaction is the driving force for helical wrapping. Moreover, the intramolecular hydrogen-bonding interaction can stabilize ideal, compact helical scaffolds. These factors determine the conformation and the binding affinity of the polysaccharide to the SWCNT. The present results can be generalized to other polymers like DNA, and shed new light on the universal principles that underlie the formation of supramolecular complexes using wrapping agents.

---

1. Introduction

On account of their unique electrical, mechanical and structural properties, carbon nanotubes (CNTs) are believed to have enormous potential and extensive future in nanodevices, drug delivery, gene therapy, gas separation.^1–7 However, the low solubility in aqueous solution and the poor bio-compatibility of CNTs greatly limit their range of applications. The emerging discipline of supramolecular wrapping chemistry⁸ takes advantage of the noncovalent interactions (i.e., π–π conjugation or hydrophobic interaction) of polymer chains and CNTs to promote wrapping of the former around the latter. Such a functionalization of CNTs is expected to help circumvent the drawback of their poor solubility and bio-compatibility while preserving their unique electrical and mechanical characteristics.^8–12 Polysaccharides,^10,11 peptides,^13–15 DNA^16–19 and organic polymers^12,20–22 are quite ordinarily used as wrapping agents.

In the case of polysaccharides, the connection between the topology, especially the linkage, of the polymer chain and the nature of the polymer–CNT complex still remains unclear. For example, the structurally similar polysaccharides, β-1,4,^23,24 α-1,4 (ref. 10 and 11) and β-1,3-glucans^25,26 are commonly utilized to solubilize CNTs through wrapping. The corresponding experimental conditions, however, are distinct. β-1,4-Glucan can be co-dispersed with single-walled carbon nanotubes (SWCNTs) under sonication,²³ whereas α-1,4-glucan can only wrap around SWCNTs in the presence of iodine, DMSO or nBuOH.¹¹ In the case of β-1,3-glucan, the helical wrapping occurs in DMSO/water mixtures.²⁵ Exploring at the atomic level the role played by glycosidic bonds is, therefore, envisioned to complement nicely the available experiments, while helping interpret them.

In this contribution, classical, all-atom MD simulations have been performed to investigate the mechanism that underlies the self-assembly in water of β-1,4, α-1,4 and β-1,3-glucan and a SWCNT into heterodimeric complexes. The stable three-dimensional (3D) arrangements of the polysaccharide–SWCNT hybrids in aqueous solution were obtained from extensive equilibrium simulations, amounting to about three microseconds aggregate time. Binding free-energy calculations were carried out to estimate the stability of the polysaccharide–SWCNT hybrids and explore the factors that promote emergence of the different arrangements. Our results provide a cogent rationalization of the distinct structural properties of the complexes formed by glucans and carbon nanotubes, and can be further generalized to other polymers to guide the design of alternate supramolecular wrapping agents.

2. Results

2.1. Spacial arrangement of the glucan–SWCNT complexes

Spontaneous wrapping. MD simulations were performed to follow the spontaneous wrapping of a β-1,4, α-1,4 and β-1,3-glucan around a (6,6) SWCNT in aqueous solution (see Table S1† for more details of all the simulations in this paper). The initial structures of the polysaccharides were produced by the GLYCAM carbohydrate builder.²⁷ The chain-like molecules were placed in the vicinity of the SWCNT surface within the cutoff distance for van der Waals interactions. Three independent runs were carried out for each molecular assembly. Fig. 1 depicts the milestone configurations in the process of spontaneous aggregation. The β-1,4-glucan quickly adsorbed on the surface of the SWCNT within 6.5 ns. Then, the chain started to curl into a helical motif. In the final 20 ns, a regular helix was formed. The same wrapping process and the similar final structure were observed reproducibly in the two other independent runs. This ultrafast wrapping of β-1,4-glucan around SWCNT is in accordance with experiment, in which the polysaccharides and SWCNT sediments were co-dissolved and dispersed under short sonication.²³

Fig. 1 Milestone configurations in the spontaneous wrapping of the (A) β-1,4, (B) α-1,4 and (C) β-1,3-glucan chain around the SWCNT. Water molecules are omitted for clarity.

Unlike β-1,4-glucan, α-1,4-glucan only adsorbed on the hollow tubular surface without wrapping it (see Fig. 1B), irrespective of the run. To wrap around the SWCNT, the α-1,4-glucan needs to unfold its original spiral structure, which is precluded by large steric hindrances with the SWCNT.²⁸ As a result, although the two ends of the polysaccharide chain curled to some extent, the middle part of the chain preserved its tiny, screw-like motif and adsorbed onto the hollow tubular surface during the 110 ns simulations. Experimental results, however, show that α-1,4-glucan can disperse SWCNT, but only under the existence of iodine, DMSO or nBuOH because the latter can induce the amylose chain to form a hollow helical conformation. The nanotube can then insert into the cavity and displace the guest molecules to form the polysaccharide–SWCNT complex (so called “pea-shooting” mechanism).^10,11 Both experimental and theoretical results suggest that it is difficult to observe the spontaneous wrapping of α-1,4-glucan directly.

In the first 14 ns of the simulation, the original helical turns of β-1,3-glucan started to uncoil as the chain adsorbed onto the surface of the SWCNT (see Fig. 1C). An irregular helix-like motif was then formed by 50 ns, and remained stable during the final 60 ns of the simulation. Akin to α-1,4-glucan, spontaneous aggregation of β-1,3-glucan did not lead to ideal helical wrapping. In experiment, helical wrapping of β-1,3-glucan occurs in water/DMSO mixtures, but the role played by DMSO still remains unclear.²⁵ The possibility of a DMSO-assisted wrapping mechanism (e.g. a “pea-shooting” mechanism similar to that of α-1,4-glucan) cannot be excluded. Additional effort is, therefore, needed to explore the wrapping mechanism of β-1,3-glucan.

Simulations starting with a tight helical wrapping structure. To determine whether the configurations obtained above correspond to the most energetically favored arrangements—in particular, whether the lack of perfect helical wrapping for α-1,4 and β-1,3-glucan is due to the insuperable barriers towards spontaneous wrapping, three additional 100 ns simulations starting with initially wrapped structures (see Fig. 2A) were performed. The final states are depicted in Fig. 2B–D. The conformations of the β-1,4 and β-1,3-glucan on the tubular surface appear to be identical to those describing spontaneous wrapping, which validates in turn the extended helix for β-1,4-glucan and the irregular helix-like motif for β-1,3-glucan, as depicted in Fig. 1A and C. Interestingly, the tight, perfect helical conformation of the α-1,4-glucan chain depicted in Fig. 2C became quite different from the irregular one obtained from spontaneous aggregation (Fig. 1B). Not too surprisingly, binding free-energy calculations relying on the MM-PBSA method²⁹ show that this binding mode is significantly more stable than the one depicted in Fig. 1B (see Table 1 and S2†). It is apparent that in spontaneous wrapping simulations, such a pronounced energy barrier is insurmountable over the time scale explored.

Fig. 2 (A) MD simulations in water starting with a tightly pre-wrapped SWCNT as an initial structure. The final 3D arrangements of (B) β-1,4, (C) α-1,4 and (D) β-1,3-glucan–SWCNT complexes after 100 ns.

Table 1 Binding free energies and their decomposition for the complexes formed by β-1,4, α-1,4 and β-1,3-glucan, and SWCNT. All quantities in kcal mol⁻¹

	ΔG	ΔEbond	ΔEangle	ΔEdihedral	ΔEColombic	EVDW	ΔGPB	ΔGSA
β-1,4-Glucan–SWCNT	−256.0	7.2	24.2	13.8	−77.1	−221.9	55.7	−58.0
α-1,4-Glucan–SWCNT	−286.2	−1.2	3.5	30.5	−182.7	−192.6	122.5	−66.3
β-1,3-Glucan–SWCNT	−230.1	4.3	13.8	8.8	−51.8	−188.3	36.7	−53.6

---

Simulation of α-1,4-glucan starting with an extended helical wrapping structure. Although Fig. 2B revealed stable helical wrapping for α-1,4-glucan around SWCNT, it is still possible that this binding mode results from an initial bias. To address this issue, an additional 80 ns simulation starting with an extended helical wrapping structure was performed. The result shows that the polysaccharide chain eventually compresses into a tight helix (see Fig. S1†), which confirms the configuration of the α-1,4-glucan–SWCNT hybrid shown in Fig. 2C. In the following discussion, only this tight helical wrapping structure will be employed for the α-1,4-glucan–SWCNT complex.

2.2. Difference in structure and stability of glucan–SWCNT hybrids

Three additional 100 ns simulations were carried out, starting from the stable structures of the β-1,4, α-1,4 and β-1,3-glucan–SWCNT complexes, as shown in Fig. 1A, 2C, and 1C, respectively. The resulting trajectories reveal that the conformations of all three polysaccharide–SWCNT hybrids are preserved. Most of the significant differences in helicity and compactness between the spatial arrangements of the hybrids can be observed directly from Fig. 1A, C and 2C. The β-1,4, α-1,4 and β-1,3-glucan–SWCNT have a left-handed, left-handed and irregular right-handed helical configuration, respectively. The α-1,4-glucan forms a much more compact helix on the surface of the SWCNT, and thus has a larger coverage. Detail of the differences between the three types of polysaccharides–SWCNT complexes can be found in the ESI.†

Binding free energy of polysaccharides to SWCNT. To evaluate their wrapping propensity, the binding free energies of the three types of polysaccharides to the SWCNTs were calculated using the MM-PBSA method,²⁹ as provided in Table 1, along with the corresponding contributions. All three polysaccharides exhibit a great propensity to wrap around SWCNT, which is in accordance with experiment. The binding affinity of the three glucans is different, following the ranking order of α-1,4-glucan > β-1,4-glucan > β-1,3-glucan. We also calculated the binding free energies per repeat unit of the glucan chains and those of the α- and β-glucose to investigate the effects of the chain length on the interaction with SWCNT. As can be inferred from Table S3 of the ESI,† for the 1,4-linked glucan, the chain length slightly impacts the binding ability of the repeat unit of glucan to the SWCNT, but for the 1,3-linked glucan, such influence becomes significant.

Inherent helical property of the polysaccharides. The inherent helicity of the polysaccharides is determined by the linkage of the polymer chain and can be mirrored by the glycosidic bond angle, θ, and the backbone dihedral angles, (φ,ψ) depicted in Fig. 3. We calculated the distribution of θ and (φ,ψ) of the polysaccharide chains in the absence and in the presence of a SWCNT. The data for the latter are extracted from the aforementioned 100 ns equilibration simulations of glucan–SWCNT complexes, and that for the former are obtained from three additional simulations of the polysaccharide chains in aqueous solution. As shown in Fig. 4, the distribution peaks of both angle θ and the backbone dihedrals (φ,ψ) only slightly shift, suggesting that the inherent helicity of the polysaccharides still contributes predominantly to the their conformation after helical wrapping.

Fig. 3 (A) Definition of the glycosidic angle θ and backbone dihedral (φ,ψ). β-1,4-Linked disaccharide as an example. (B) Backbone atom names of 1,4 and 1,3-linked glucose. The dihedral angle φ is defined as C3–C4–O4–C1′ for β-1,4, and α-1,4-glucan and C4–C3–O3–C1′ for β-1,3-glucan and ψ is defined as O5′–C1′–O4–C4 for β-1,4, and α-1,4-glucan and O5′–C1′–O3–C3 for β-1,3-glucan.

Fig. 4 Distributions of backbone valence angle θ and dihedrals (φ,ψ) of the polysaccharide chains with and without the SWCNT, together with the free-energy profiles as a function of angle θ and dihedral (φ,ψ). (A)–(C) Distributions and free-energy profiles of valence angle θ of (A) β-1,4, (B) α-1,4 and (C) β-1,3-glucan. (D)–(F) Distributions and free-energy profiles of dihedrals (φ,ψ) of (D) β-1,4, (E) α-1,4 and (F) β-1,3-glucan. The purple and orange ellipses indicate the distributions of (φ,ψ) of the free polysaccharides in water and those wrapping around SWCNT, respectively. The full distributions are provided in Fig. S6.†

The one-dimensional free-energy profile (or potential of the mean force, PMF) of angular bending as a function of glycosidic bond angle θ, and the two-dimensional free-energy landscape of torsional deformation as a function of the torsional angles (φ,ψ) were calculated for each linkage. As depicted in Fig. 4, the distribution peak of θ and (φ,ψ) agrees well with the minimum of the free-energy profile for both the free polysaccharide and its wrapping conformations, indicating that in the stable structures of the polysaccharide–SWCNT complexes the chains chiefly preserved their low-energy conformation.

van der Waals and hydrophobic interactions of glucans with SWCNTs. The van der Waals (VDW) interaction of glucan and SWCNT is the predominant contribution to the binding free energy in each case. In particular, the β-1,4-glucan–SWCNT hybrid possesses the most favorable VDW interactions. The average distance between the polysaccharides and the SWCNT surface was calculated (see Fig. 5A) and indicates that the β-1,4-glucan chain lies closest to the tubular surface. This difference in the distance is likely to stem from the orientation of the pyranose rings with respect to the surface of the SWCNT. The number of pyranose rings in the chains parallel to the tubular surfaces was computed, as shown in Fig. 5B. As expected, the β-1,4-glucan has the largest number of parallel rings, while the β-1,3-glucan, the smallest, in line with the VDW contribution in Table 1.

Fig. 5 (A) Average distance between each hydrophobic carbon atom of the polysaccharides and the SWCNT surface during the 100 ns equilibrium simulation and (B) number of pyranose rings for the three types of polysaccharides oriented parallel to the tubular surface.

The nonpolar solvation free energy, ΔG_SA, regarded as the contribution of hydrophobic interactions, is also favorable for the wrapping in all cases, due to the coverage of the hydrophobic surface of the SWCNT by the chains. The largest coverage rate results in the most favorable hydrophobic interaction for α-1,4-glucan (see Fig. S3†), which can be ascribed to the large number of parallel pyranose rings concealing the hydrophobic tubular surface and the high compactness between the helical turns. Burial of the hydrophobic surface is a key prerequisite for the assembly of the polysaccharide–SWCNT hybrids. Therefore, it can be concluded that VDW and hydrophobic interactions of polysaccharides and SWCNTs form the driving force responsible for helical wrapping.

Intra- and intermolecular hydrogen-bond interactions. Coulombic interactions follow the order α-1,4 ≫ β-1,4 > β-1,3. Fig. 6 reveals the number of intramolecular hydrogen bonds formed in the glucan chains wrapped on the SWCNTs and in the same chains, albeit in the absence of SWCNT (free state in water). As can be seen, the intramolecular hydrogen bonds of all three glucans increased after wrapping on the SWCNTs. The α-1,4-glucan can form hydrogen bonds between adjacent helical turns, resulting in many more hydrogen bonds compared to the other two polysaccharides, and leading to a compact helical conformation on the SWCNT surface. The β-1,4 and the β-1,3-glucan can only form intramolecular hydrogen bonds between adjacent monomers, leading to an increase in their conformational entropies compared to the α-1,4-glucan. The polar interaction, ΔG_PB, can be largely attributed to the intermolecular hydrogen bonds formed by the polysaccharides and the water molecules. The more intramolecular hydrogen bonds in the chain, the less intermolecular hydrogen bonds between the glucans and the solvent, as shown in Table 1.

Fig. 6 Number of intramolecular hydrogen bonds formed in the β-1,4, α-1,4 and β-1,3-glucans wrapping around the SWCNT (with SWCNT) and in the free state (without SWCNT).

Effect of SWCNTs on spatial arrangements of hybrids. Four types of nanotubes, viz., a (6,6), a (8,8), a (10,10) and a (10,0) SWCNT were considered (see Table S1†). In the initial structure of each assay, the β-1,4-glucan chain was wrapped as a helix around the nanotube. 100 ns simulations were then performed in aqueous solution. The final configurations are found to be similar for all four assemblies. The pitch of the helix was monitored in the final 50 ns, and is shown in Fig. S4 and Table S4 of the ESI.† Analysis of the variance of the results suggests that there are no significant differences among the pitches within the different polysaccharide–SWCNT complexes, indicative that the diameter and the chirality of the SWCNTs may have little impact on the spatial arrangements of hybrids. However, the binding free energies of β-1,4-glucan to the SWCNTs with different diameters suggest that the larger the diameter of the SWCNT, the stronger the binding (see Table S5 of the ESI†). Table S5† is also suggestive of a subtle influence of the chirality of the SWCNT on the binding affinity of glucan to the nanotube. More systematic investigations remain needed to explore the effect of the SWCNTs on the structure of the complexes, which goes beyond the scope of this work.

3. Discussion and perspective

The present results show that the glycosidic bonds of polysaccharides plays a crucial role in the three-dimensional arrangement of the polysaccharide–SWCNT hybrids. The structures of these hybrids determine their applications. For example, corona phase molecular recognition (CoPhMoRe)^30,31 is a novel method to selectively adsorb and recognize small molecules. In this method, supramolecular wrapping hybrids with distinct pitches are used to include different organic molecules in the interstices formed between two adjacent turns. Therefore, based on our results, only β-1,4 and β-1,3-glucans can be potential candidates of wrapping agents for CoPhMoRe, because the helices formed by α-1,4-glucan are too tight to include any molecule.

More generally, the inherent helicity of a polysaccharide determined by its glycosidic bonds is basically preserved in the wrapping process, mainly impacting the wrapping mode in the presence of a SWCNT. This rule can be generalized to other polysaccharides. For example, the wrapping mode of chitosan (β-1,4 linked glucosamine)³² is akin to that of β-1,4-glucan, which implies that the β-1,4 linked glycosidic bond contributes to the three-dimensional arrangement of polysaccharide–SWCNT complexes. The conformation of alginic acid (1,4 linked β-D-mannuronate and α-L-guluronate)³³ on the SWCNT surface is an irregular helix, owing to the mixture of β- and α-linkage, which makes it difficult for polysaccharide chains to adapt to the SWCNT surface and form ideal helices.

The radius and chirality of the SWCNT seem to have little effect on the three-dimensional arrangement of polysaccharide–SWCNT hybrids. However, specific sequence of DNA can selectively associate with SWCNTs endowed with specific radius and chirality.^18,34 The difference between DNA and polysaccharides is rooted in their distinct association mechanism. Assembly of a polysaccharide and a SWCNT is driven by hydrophobic interaction, but that of DNA and a nanotube is through π–π stacking.³⁵ π–π stacking is largely affected by the relative location of the benzene ring of the DNA with respect to the SWCNT, thus being highly radius- and chirality-dependent.

As for many other chain-like molecules, such as DNA^36–39 and organic polymers,^21,40–42 there should be other factors aside from the linkage of the polymers that affect the three-dimensional arrangement of polymer–SWCNT hybrids. For example, It is suggested that polymers with stiff and semi-flexible backbones tend to wrap around the SWCNT with more distinct conformations than those with flexible backbones,^43,44 which partly supports and rationalizes our conclusions. Different side groups of the polymer were also found to lead to different conformations of the chain-like molecule on the surface of SWCNT.⁴⁵ In addition, when the concentration in polysaccharides increases, interchain effects may be observed, to the extent that the CNT can be wrapped by more than one polysaccharide chain (see the ESI† for more discussion). A large number of experiments and simulations are, therefore, needed to establish a general set of rules for supramolecular wrapping chemistry. The present study, focusing on the effect of glycosidic bonds on the structures of polysaccharide–SWCNT complexes, lays the foundation stone towards such universal rules.

4. Conclusion

The discrepant structural properties of β-1,4, α-1,4 and β-1,3-glucan–SWCNT complexes can be ascribed to the following factors—(i) the inherent helicity of the glucans, mainly impacting the wrapping mode of the chain, (ii) the hydrophobic interaction of pyranose ring with the SWCNT, which plays a key role responsible for the initial step of wrapping process, and (iii) the intramolecular hydrogen bonds, which are of paramount importance for an ideal, tight helix. All these three factors are related to the glycosidic bond linkage, the corresponding contributions responsible for the large structural differences of the complexes formed by glucans and SWCNT.

The present contribution provides the microscopic detail of polysaccharide chains with different glycosidic bonds interacting with a SWCNT, and reveals the fundamental principles of how the topology of the polymer chains affects the configuration and the nature of the supramolecular wrapping hybrids. The results reported herein are envisioned to guide the chemist in the selection and the design of supramolecular wrapping agents for the specific binding of guest molecules, or for the effective interaction with DNA, notably in the context of nanotube-based gene delivery vehicles. Moreover, the detailed analysis of the factors responsible for the structural difference of the complexes constitutes a preliminary exploration of the general rules that underlie supramolecular wrapping chemistry.

5. Simulation details

5.1. Models

The structural formulas of β-1,4, α-1,4 and β-1,3-glucan are provided in Fig. S4 of the ESI.† On the basis of the unit-cell parameters, 30-mer polysaccharide chains were constructed. As can be seen in Fig. 1, the initial structure of β-1,4-glucan is completely extended, while α-1,4-glucan possesses a tight helical shape and the β-1,3 chain corresponds to an intermediate case. The initial conformations of β-1,4, α-1,4 and β-1,3-glucan used in this study were generated by the GLYCAM carbohydrate builder,²⁷ which assembles polysaccharides chains close to their crystal structures. To eliminate possible edge effects, an infinitely long SWCNT was built. The detailed steps of the preparation of the initial structures are provided in the ESI.† The CHARMM36 carbohydrate force field,^46,47 the CHARMM general force field (CGenFF)⁴⁸ and the TIP3P model,⁴⁹ which have been extensively validated and are widely used to describe the interaction of (bio)macromolecules with carbon nanotube/graphene in aqueous solution,^32,39,50 were adopted to model glucans, SWCNTs and water, respectively. The atoms of the SWCNT were described as sp² aromatic carbon parameters of the CGenFF devoid of a net atomic charge and the equilibrium length of the C–C bonds was 1.42 Å. The general description of the molecular assemblies considered in this study is summarized in Table S1 of the ESI.†

5.2. Molecular dynamics simulations

All the atomistic MD simulations reported herein were performed using the parallel, scalable program NAMD 2.10.⁵¹ Covalent bonds involving hydrogen atoms were constrained to their equilibrium length by means of the SHAKE/RATTLE^52,53 and SETTLE algorithms⁵⁴ for the glucan and water molecules, respectively. The r-RESPA multiple time-step algorithm was employed to integrate the equations of motion with a time step of 2 and 4 fs for short- and long-range interactions, respectively.⁵⁵ Long-range electrostatic forces were evaluated using the particle mesh Ewald (PME) scheme.⁵⁶ In the PME scheme, charges are interpolated onto a grid. A grid spacing of 1.0 Å and a cubic spline interpolation were used. A 10⁻⁶ tolerance for the direct space sum cutoff was chosen. A smoothed 12 Å spherical cutoff was applied to truncate van der Waals and short-range electrostatic interactions. Periodic boundary conditions (PBCs) were applied in the three directions of Cartesian space. The position of the carbon atoms of the SWCNT was restrained with weak harmonic restraints, viz., 1.0 kcal mol⁻¹ Å⁻². Visualization and analyses of the MD trajectories were performed with the VMD package⁵⁷ and numerical python. Each molecular system first underwent 2 ns of NPT ensemble equilibration at 300 K and 1 atm, respectively, employing Langevin dynamics and the Langevin piston pressure control.⁵⁸ Then, MD simulations were performed in the canonical ensemble at the same temperature.

5.3. Free-energy calculations

Calculation of the binding affinity of polysaccharides. The MM-PBSA method was employed to calculate the binding free energy of the polysaccharide–SWCNT hybrids. The dielectric constants of glucan and the solvent were set to 2.0 and 78.54, respectively. The solvent radius was set to 1.4 Å and the grid spacing was 0.5 Å in each dimension. iAPBS,⁵⁹ the interface calling APBS⁶⁰ in NAMD, was used to calculate the Poisson–Boltzmann contribution to the binding free energy. Three 20 ns simulations, characterizing β-1,4, α-1,4 and β-1,3-glucan in bulk water, together with three 100 ns simulations characterizing the stable three-dimensional arrangement of the three types of polysaccharide–SWCNT hybrids were performed to provide the trajectories needed in the free-energy calculations.

Calculation of the PMF characterizing the conformational penalty. Free-energy calculations were carried out, utilizing the multiple-walker adaptive biasing force (MW-ABF) algorithm,^61–64 in which exchange across the different copies of information on local estimates of the gradient, dG(ξ)/dξ—where ξ denotes the transition coordinate, enhances ergodic sampling. The instantaneous value of the force was stored in bins 1° wide for the one-dimensional PMF and 3° wide for the two-dimensional free-energy landscape. The total sampling time required to determine the six PMFs was 80 ns and 320 ns for the one- and two-dimensional free-energy calculations, respectively.

Acknowledgements

The study was supported by National Natural Science Foundation of China (No. 21373117), the Natural Science Foundation of Tianjin, China (No. 13JCYBJC18800), MOE Innovation Team (IRT13022) of China and the Ph.D. Candidate Research Innovation Fund of Nankai University. The GENCI and CINES, Montpellier, France, and NSCC, Tianjin, China, are gratefully acknowledged for provision of generous amounts of CPU time. The Cai Yuanpei program is also appreciatively acknowledged for its support of the international collaboration between the research groups of C.C. and W.C.

References

1. A. Bianco, K. Kostarelos and M. Prato, Curr. Opin. Chem. Biol., 2005, 9, 674–679.
2. R. H. Baughman, A. A. Zakhidov and W. A. de Heer, Science, 2002, 297, 787–792.
3. D. Tasis, N. Tagmatarchis, A. Bianco and M. Prato, Chem. Rev., 2006, 106, 1105–1136.
4. F. Lu, L. Gu, M. J. Meziani, X. Wang, P. G. Luo, L. M. Veca, L. Cao and Y. P. Sun, Adv. Mater., 2009, 21, 139–152.
5. Y. Jiao, A. Du, M. Hankel and S. C. Smith, Phys. Chem. Chem. Phys., 2013, 15, 4832–4843.
6. G. Cirillo, S. Hampel, U. G. Spizzirri, O. I. Parisi, N. Picci and F. Iemma, BioMed Res. Int., 2014, 2014, 825017.
7. Y.-L. Zhao and J. F. Stoddart, Acc. Chem. Res., 2009, 42, 1161–1171.
8. M. Numata and S. Shinkai, Chem. Commun., 2011, 47, 1961–1975.
9. Y. Liu, P. Liang, H. Y. Zhang and D. S. Guo, Small, 2006, 2, 874–878.
10. O.-K. Kim, J. Je, J. W. Baldwin, S. Kooi, P. E. Pehrsson and L. J. Buckley, J. Am. Chem. Soc., 2003, 125, 4426–4427.
11. A. Star, D. W. Steuerman, J. R. Heath and J. F. Stoddart, Angew. Chem., Int. Ed., 2002, 41, 2508–2512.
12. P. Bilalis, D. Katsigiannopoulos, A. Avgeropoulos and G. Sakellariou, RSC Adv., 2014, 4, 3060–3083.
13. G. R. Dieckmann, A. B. Dalton, P. A. Johnson, J. Razal, J. Chen, G. M. Giordano, E. Muñoz, I. H. Musselman, R. H. Baughman and R. K. Draper, J. Am. Chem. Soc., 2003, 125, 1770–1777.
14. D. R. Samarajeewa, G. R. Dieckmann, S. O. Nielsen and I. H. Musselman, Nanoscale, 2012, 4, 4544–4554.
15. C. C. Chiu, G. R. Dieckmann and S. O. Nielsen, Pept. Sci., 2009, 92, 156–163.
16. E. J. Petersen, X. Tu, M. Dizdaroglu, M. Zheng and B. C. Nelson, Small, 2013, 9, 205–208.
17. D. Roxbury, J. Mittal and A. Jagota, Nano Lett., 2012, 12, 1464–1469.
18. X. Tu, S. Manohar, A. Jagota and M. Zheng, Nature, 2009, 460, 250–253.
19. M. Zheng, A. Jagota, E. D. Semke, B. A. Diner, R. S. McLean, S. R. Lustig, R. E. Richardson and N. G. Tassi, Nat. Mater., 2003, 2, 338–342.
20. A. Star, J. F. Stoddart, D. Steuerman, M. Diehl, A. Boukai, E. W. Wong, X. Yang, S. W. Chung, H. Choi and J. R. Heath, Angew. Chem., Int. Ed., 2001, 40, 1721–1725.
21. Y. K. Kang, O. Lee, P. Deria, S. H. Kim, T. Park, D. A. Bonnell, J. G. Saven and M. J. Therien, Nano Lett., 2009, 9, 1414–1418.
22. T. Li, L. Ma, R. Bao, G. Qi, W. Yang, B. Xie and M. Yang, J. Mater. Chem. A, 2015, 3, 5482–5490.
23. M. G. Adsul, D. A. Rey and D. V. Gokhale, J. Mater. Chem., 2011, 21, 2054–2056.
24. L. Li, L. Meng, X. Zhang, C. Fu and Q. Lu, J. Mater. Chem., 2009, 19, 3612–3617.
25. M. Numata, M. Asai, K. Kaneko, A.-H. Bae, T. Hasegawa, K. Sakurai and S. Shinkai, J. Am. Chem. Soc., 2005, 127, 5875–5884.
26. M. Numata, M. Asai, K. Kaneko, T. Hasegawa, N. Fujita, Y. Kitada, K. Sakurai and S. Shinkai, Chem. Lett., 2004, 33, 232–233.
27. Woods Group (2005–2015), GLYCAM Web, Complex Carbohydrate Research Center, University of Georgia, Athens, GA, http://www.glycam.com.
28. Y. Liu, C. Chipot, X. Shao and W. Cai, Nanoscale, 2012, 4, 2584–2589.
29. P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan and W. Wang, Acc. Chem. Res., 2000, 33, 889–897.
30. S. Kruss, M. P. Landry, E. Vander Ende, B. M. Lima, N. F. Reuel, J. Zhang, J. Nelson, B. Mu, A. Hilmer and M. Strano, J. Am. Chem. Soc., 2014, 136, 713–724.
31. G. Bisker, J. Ahn, S. Kruss, Z. W. Ulissi, D. P. Salem and M. S. Strano, J. Phys. Chem. C, 2015, 13876–13886.
32. Y. Liu, C. Chipot, X. Shao and W. Cai, J. Phys. Chem. C, 2011, 115, 1851–1856.
33. Y. Liu, C. Chipot, X. Shao and W. Cai, J. Phys. Chem. B, 2010, 114, 5783–5789.
34. A. Shankar, J. Mittal and A. Jagota, Langmuir, 2014, 30, 3176–3183.
35. R. R. Johnson, A. Johnson and M. L. Klein, Small, 2010, 6, 31–34.
36. R. R. Johnson, A. Kohlmeyer, A. C. Johnson and M. L. Klein, Nano Lett., 2009, 9, 537–541.
37. R. R. Johnson, A. C. Johnson and M. L. Klein, Nano Lett., 2008, 8, 69–75.
38. D. Roxbury, A. Jagota and J. Mittal, J. Am. Chem. Soc., 2011, 133, 13545–13550.
39. M. W. Chien, R. R. Johnson, S. R. Pillai, S. R. Singh and A. C. Johnson Jr, J. Phys. Chem. C, 2014, 118, 2209–2214.
40. A. O. Furmanchuk, J. Leszczynski, S. Tretiak and S. V. Kilina, J. Phys. Chem. C, 2012, 116, 6831–6840.
41. C. D. von Bargen, C. M. MacDermaid, O.-S. Lee, P. Deria, M. J. Therien and J. G. Saven, J. Phys. Chem. B, 2013, 117, 12953–12965.
42. M. Shan, Q. Xue, T. Lei, W. Xing and Z. Yan, J. Phys. Chem. C, 2013, 117, 16248–16255.
43. S. S. Tallury and M. A. Pasquinelli, J. Phys. Chem. B, 2010, 114, 9349–9355.
44. I. Gurevitch and S. Srebnik, J. Chem. Phys., 2008, 128, 144901.
45. S. S. Tallury and M. A. Pasquinelli, J. Phys. Chem. B, 2010, 114, 4122–4129.
46. E. R. Hatcher, O. Guvench and A. D. MacKerell Jr, J. Chem. Theory Comput., 2009, 5, 1315–1327.
47. O. Guvench, E. Hatcher, R. M. Venable, R. W. Pastor and A. D. MacKerell Jr, J. Chem. Theory Comput., 2009, 5, 2353–2370.
48. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, J. Comput. Chem., 2010, 31, 671–690.
49. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
50. S. Iliafar, J. Mittal, D. Vezenov and A. Jagota, J. Am. Chem. Soc., 2014, 136, 12947–12957.
51. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
52. H. C. Andersen, J. Comput. Phys., 1983, 52, 24–34.
53. J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
54. S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962.
55. M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001.
56. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
57. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
58. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621.
59. R. Konecny, N. A. Baker and J. A. McCammon, Comput. Sci. Discovery, 2012, 5, 015005.
60. N. A. Baker, D. Sept, S. Joseph, M. J. Holst and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10037–10041.
61. J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, J. Phys. Chem. B, 2014, 119, 1129–1151.
62. J. Comer, B. Roux and C. Chipot, Mol. Simul., 2014, 40, 218–228.
63. K. Minoukadeh, C. Chipot and T. Lelièvre, J. Chem. Theory Comput., 2010, 6, 1008–1017.
64. J. Comer, J. C. Phillips, K. Schulten and C. Chipot, J. Chem. Theory Comput., 2014, 10, 5276–5285.

---

Footnote

† Electronic supplementary information (ESI) available: Detail of the molecular assays and the simulations. Time evolution of the pitch in the glucans. Time evolution of the coverage of SWCNT in the three glucan–SWCNT hybrids. Binding free energies for the glucan–SWCNT complexes. Differences between three polysaccharide–SWCNT hybrids. Chain length of the polysaccharides participating in the wrapping. Effects of the concentration of the glucan. Preparation of initial structures. Detailed discussion of temperature-control algorithm. See DOI: 10.1039/c5ra17472d

---