Evidence of blue-shifting N–H⋯N hydrogen bonding despite elongation of the N–H bond

Abstract

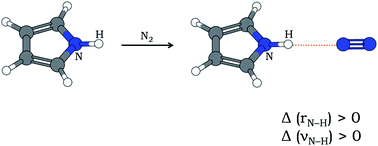
In most cases of X–H⋯Y hydrogen bonding (X is an electronegative atom and Y is any electron-rich center), the X–H bond gets elongated and the stretching frequency of X–H (ν_X–H) gets red-shifted. Relatively fewer cases of blue-shifting H-bonding are also known, where the X–H bond contracts leading to an increase in ν_X–H. Here is presented the first experimental report of blue-shifting N–H⋯N H-bonding that accompanies an increase in N–H bond length as evident from quantum chemistry computations. Pyrrole and N₂ have been shown to form N–H⋯N hydrogen bond in an ‘annealed’ N₂ matrix, where both doped (pyrrole) and dopant (nitrogen) molecules had scope to align themselves and form stable H-bonded clusters. The infrared spectrum of the annealed matrix shows a blue shift of ν_N–H by 7 cm⁻¹. Computation of anharmonic frequencies at the MP2/6-31+G(d) level of theory reflects the observed blue shift despite N–H bond lengthening after H-bond formation.

---

The phenomenon of ‘blue-shifting hydrogen bonding’, where the stretching frequency of X–H (ν_X–H) is shifted to a higher value in a hydrogen bonded X–H⋯Y type cluster, has been extensively discussed in recent literature.^1–32 In most of the studies reported to date, a very weakly acidic C–H group has been shown to display blue-shifting H-bonding either with classical acceptors, i.e., the electronegative atom Y having lone pair(s) of electrons^{5–8,11–20,22,23,25–27,29–32} or non-classical acceptors with π-electron systems, e.g., aromatic group.^6,14,25 The proposed mechanisms, with many different approaches, were aimed at shortening of X–H bond, and the blue shift of ν_X–H was considered a direct consequence of X–H bond shortening. Details of the proposed mechanisms are not reiterated here. In short, electron redistribution^{1–21,23–32} and the repelling electric field of Y moiety²² after H-bond formation were ascribed to X–H bond shortening. But a universal correlation between the change in X–H bond length and extent of spectral shift (Δν_X–H) has never been established. It is not the equilibrium X–H bond length, but the potential energy surface (PES) of X–H stretching mode, that correlates directly with ν_X–H. One can imagine an equilibrium geometry of weakly bound X–H⋯Y cluster where the factors responsible for X–H bond lengthening (e.g., hyperconjugation from Y to σ* of X–H) are slightly dominating over repulsive electric field of Y, but the bond (X–H) stretching potential might be lifted due to the latter, thereby increasing the stretching frequency. Of course, subtle balance of multiple forces leading to the said observation, if at all possible, is expected to be seen in weak H-bonded systems. Such a model system is dealt with in this report.

The model system is the N–H⋯N hydrogen bonded 1 : 1 cluster between pyrrole and N₂. Geometry optimization of this cluster by various levels of quantum chemistry computations shows a linear geometry of N–H⋯N≡N moiety (Fig. 1). The bonding between NH (of pyrrole) and N₂ is further ascertained by the existence of bond critical point between the two moieties using AIM theory.³³ Topological diagram citing bond critical points is provided in ESI.†

Fig. 1 Optimized geometries of (a) pyrrole⋯N₂ and (b) pyrrole⋯acetonitrile clusters at MP2/6-31+G(d) level of theory. Grey, blue and white spheres represent carbon, nitrogen and hydrogen atoms respectively.

The advantages of using this H-bonding prototype are the following. (a) The N–H⋯N≡N geometry is linear (see Fig. 1) which minimizes the extent of dispersion interaction from remote parts of pyrrole and N₂ moieties. Thus the intermolecular interaction would exclusively be H-bonding. (b) Vibrational energy distribution over internal coordinates, calculated by the method of Pulay and Torok,³⁴ of pyrrole shows that the N–H stretching vibration is exclusively a local mode (contribution of ν_N–H to the normal mode energy is ∼100%). Thus, the intermode couplings are negligible and the diagonal anharmonicity (anharmonicity along normal mode vector) accounts for the correct PES of this normal mode. For the pyrrole⋯N₂ cluster, the second largest contributor to the N–H stretching normal mode is ν_H⋯N (hydrogen bond stretching) which contributes only ∼0.5% to the normal mode energy. Also, the beauty of the system is that both the N–H and H⋯N stretches are collinear. Thus, the diagonal anharmonicity of the N–H stretching mode incorporates the effect due to coupled H⋯N stretch. Other coupling terms are very small and can be comfortably neglected. Such simplification, intrinsic to the system, improves accuracy in prediction of ν_N–H as additional approximations are required to incorporate intermode couplings.

All quantum chemistry computations have been carried out by GAMESS [Version: 5 Dec 2014 (R1)] program package.³⁵ As the H-bonding interaction between pyrrole and N₂ is expected to be at the weaker end, and consequently the spectral shift (Δν_N–H) to be small, a careful selection of theoretical level is necessary to depict the real picture of the system. In the present study, the widely accepted Møller–Plesset second order perturbation (MP2) theory has been used to model the N–H stretching frequency. It is a known issue that the accuracy in prediction depends on the basis set selected, and there is no any unanimous rule (as will be evident very shortly) that a higher basis set must produce more accurate results. Thus to ascertain the accuracy in theoretical prediction the following procedure is adopted. First, the diagonal anharmonicity of the N–H stretching mode of pyrrole is computed over 64 grid points using a series of different basis sets and compared with experimental data in gas phase. The following Pople type basis sets: 6-31G(d,p), 6-31+G(d), 6-31+G(d,p), 6-311++G(d,p), and also the aug-cc-pVDZ basis set have been used for computations. Results obtained from the said computations are summarized in ESI.† The best match of the computed anharmonic frequency of N–H stretching mode is found for the MP2/6-31+G(d) level of theory which predicts the ν_N–H of pyrrole as 3532 cm⁻¹, while the reported experimental value in gas phase is 3531 cm⁻¹.³⁶ Notably, the higher basis sets, viz., 6-31+G(d,p), 6-311++G(d,p) and aug-cc-pVDZ are found to be worse in predicting the ν_N–H value of pyrrole. Reliability of MP2/6-31+G(d) theoretical level and the adopted approach to compute anharmonic frequency have further been checked for some H-bonded clusters of pyrrole. Obviously, the systems are so chosen that the intermode couplings with ν_N–H are negligibly small. As experimental data for H-bonded pyrrole⋯N₂ cluster in gas phase is currently not available in literature, a structurally similar N–H⋯N hydrogen bonded system, pyrrole⋯acetonitrile (Fig. 1), has been used for the purpose. While the experimental value of ν_N–H of pyrrole⋯acetonitrile is 3437 cm⁻¹ in gas phase,³⁷ the computed anharmonic frequency for the same at MP2/6-31+G(d) theoretical level is 3439 cm⁻¹. The same theoretical approach to pyrrole homo-dimer predicts ν_N–H values as 3520 and 3444 cm⁻¹ for free and H-bonded (N–H⋯π) N–H moieties, respectively, while the reported gas-phase values³⁶ are 3522 and 3444 cm⁻¹. All these data for ν_N–H are summarized in Table 1 for a quick comparison between experimental and computed values.

Table 1 Comparison of theoretical predictions for ν_N–H values (anharmonic) at MP2/6-31+G(d) level with the corresponding experimental values at gas phase

Molecule/cluster	Predicted νN–H (cm^−1)	Experimental νN–H^a (cm^−1)
a Values taken from ref. 36 and 37.
Pyrrole	3532	3531
Pyrrole⋯acetonitrile	3439 (N–H⋯N bonded)	3437
Pyrrole⋯pyrrole	3520 (Free N–H)	3522
Pyrrole⋯pyrrole	3444 (N–H⋯π bonded)	3444
Pyrrole⋯N2	3540 (N–H⋯N bonded)	No previous data

---

Such close agreements between experimental observations and theory are very encouraging and indicate the acceptability of MP2/6-31+G(d) level of theory for the present work. The same theoretical level was also previously used for prediction of blue-shifting hydrogen bonds in many other systems.^5,8,29 Importantly, for pyrrole⋯N₂ cluster, the MP2/6-31+G(d) computational level predicts a blue shift of ν_N–H by 8 cm⁻¹ (see Table 1). At the same time it predicts a lengthening of N–H bond by 0.0007 Å. Similar bond (N–H) lengthening is predicted by all other theoretical levels (see ESI†). Thus, the claim of blue-shifted ν_N–H, in spite of lengthening of N–H bond, gets strong support from quantum chemistry computations at MP2/6-31+G(d) level of theory for hydrogen bonded cluster between pyrrole and N₂. For deeper scrutiny of the said observations, a scan of H⋯N bond length is done, and at each scan point all the geometrical parameters, except the fixed H⋯N bond length, are allowed to optimize. This treatment shows an energy minimum (corresponding to equilibrium geometry) at H-bond length of 2.37 Å (Fig. 2). As the H-bond length decreases, the N–H bond increases in length and never goes through any minimum (see Fig. 2). Such behavior was earlier ascribed to ‘proper’ H-bonding, where a red shift of ν_X–H was expected to occur because of elongated X–H bond in equilibrium geometry.¹³ As the spectral shift in the present case is opposite (blue shift), a further scrutiny of the H⋯N bond energy is done. Energy decomposition analysis (EDA), as implemented in GAMESS, is carried out to evaluate H⋯N bond energy at each point of previous scan. The same EDA method was earlier used to obtain reasonable results for several H-bonded clusters.³⁸ Interestingly, in the present study, the outcomes of EDA over the entire scan range of H⋯N bond length vary in a systematic manner and reveal that the H-bond is strongest when it is little longer (2.52 Å) than that at equilibrium geometry (see Fig. 2). Now, the stretching modes of N–H and H⋯N are coupled. An extra potential exerted upon N–H stretching mode by the adjacent hydrogen bonded part at equilibrium geometry lifts the value of ν_N–H. Eventually, the hydrogen bond, H⋯N, becomes ‘blue-shifting’ in spite of elongated N–H bond.

Fig. 2 Summary of H⋯N scan results at MP2/6-31+G(d) level of theory. Units along vertical axis for the three parameters are different. Total energy changes from −318.7590 to −318.7596 Ha, H⋯N bond energy from −0.23 to 0.87 kcal mol⁻¹, and N–H bond length from 1.01237 to 1.01620 Å on going from the corresponding H⋯N bond length 4.47 to 1.97 Å.

The infrared spectra of pyrrole-doped N₂ matrix have been recorded at a temperature range of 8–28 K (Fig. 3). The binding energy of the pyrrole⋯N₂ cluster being very small, only ∼1 kcal mol⁻¹ (BSSE corrected) according to the calculation at MP2/6-31+G(d) level, its natural abundance in a static gas cell at room temperature must be extremely small. However, in the present study, it is shown that the same H-bonded cluster can be generated in relatively large abundance within a cold N₂ matrix, and studied by infrared spectroscopy. For preparation of the seeded matrix, a mixture of pyrrole vapor and nitrogen gas at a ratio of 1 : 1000 at room temperature (22 °C) was diffused through a needle and deposited on the cold (8 K) KBr window in the matrix isolation chamber under high vacuum (∼10⁻⁶ mbar). The ν_N–H band of the initially deposited matrix appears as multiplet centered at ∼3512 cm⁻¹, and the overall width of the multiplet is ∼7 cm⁻¹ (spectrum ‘a’, Fig. 3). This multiplet corresponds to the ν_N–H of pyrrole monomer trapped in different matrix sites. Appearance of such site splitting in matrices is common and cited earlier.³⁹ Notably, the solvation shift (by N₂ matrix) of ν_N–H from reported gas-phase data (and prediction at MP2/6-31+G(d) level of theory) is ∼20 cm⁻¹ (compare with Table 1). There is no any significant IR band(s) except for pyrrole monomer in the spectrum ‘a’ of Fig. 3. However, dramatic changes occur when the matrix is annealed by heating it slowly up to 28 K and then cooling back to 8 K (a–c, Fig. 3). Spectrum ‘c’ in Fig. 3 corresponds to the resulting annealed matrix. Two stable site bands, centered at 3509 and 3514 cm⁻¹ still persist in annealed matrix, and several new features develop. The overall spectrum of annealed matrix, keeping in mind the solvation shift by ∼20 cm⁻¹, looks quite similar to the reported gas phase spectra of pyrrole monomer and its higher clusters,³⁶ except for some extra peaks in the present case. Thus by a comparison with gas phase spectra, the peak at 3424 cm⁻¹ in annealed matrix can be assigned to the pyrrole dimer, and the broad feature near 3380 cm⁻¹ can be assigned to higher homo-clusters of pyrrole. An interesting new feature observed in the present study is a distinct blue-shifted peak at 3519 cm⁻¹ which is practically absent in the spectrum of freshly prepared matrix, but appears after heating the matrix to a higher temperature (a–b, Fig. 3). Possibility of any blue-shifted peak due to homo-clusters of pyrrole can be ruled out from previous reports in gas phase³⁶ as well as Ar and Xe matrices.³⁹ Thus, the 3519 cm⁻¹ peak must arise out of some specific interaction between the guest pyrrole molecules and the matrix molecules, i.e., N₂. In freshly prepared matrix, the relative orientations of pyrrole and N₂ molecules were quite random. Rigidity of the matrix opposed any reorientation of pyrrole and N₂ molecules that could establish required linearity for effective N–H⋯N≡N hydrogen bonding. When the temperature of the matrix is raised, the matrix softens and a number of pyrrole and N₂ molecules reorient to form N–H⋯N≡N hydrogen bond as shown in Fig. 1. Thus, the 3519 cm⁻¹ peak (spectra ‘b’ & ‘c’, Fig. 3) has been assigned to the ν_N–H of 1 : 1 cluster between pyrrole and N₂. The observed blue shift (∼7 cm⁻¹) is again in good agreement with the prediction (+8 cm⁻¹) by MP2/6-31+G(d) level of theory. The bottom panel of Fig. 3 depicts the computed spectral positions (with 20 cm⁻¹ red shift for solvation effect) of pyrrole monomer, its homo-dimer as well as pyrrole⋯N₂ cluster. The match of computed spectral positions with those observed in annealed matrix is outstanding.

Fig. 3 Infrared spectra of pyrrole in N₂ matrix recorded (a) just after deposition at 8 K and (b) after heating the matrix to 20 K. Spectrum (c) represents the matrix which was annealed by gradually heating it to 28 K and then cooling back to 8 K. Spectrum (d) shows the calculated spectral positions for pyrrole monomer (M), its homo-dimer (D) and pyrrole⋯N₂ cluster (C). These calculated values were obtained by subtracting 20 cm⁻¹ (as solvation shift by the matrix) from the corresponding values computed for isolated (gas phase) molecules/clusters at MP2/6-31+G(d) level of theory. Intensities of the calculated transitions are arbitrary, only to show their spectral positions.

In conclusion, this is the first report of infrared spectroscopic detection of blue-shifting NH⋯N bonding between pyrrole and N₂, and the finding is well supported by quantum chemistry computation at MP2/6-31+G(d) theoretical level. The study shows that the shortening of equilibrium bond length of H-bond donor (X–H) is not a mandatory criterion for occurrence of blue-shifting H-bonding, especially when the binding energy is very small. The importance of anharmonic correction in frequency is evident for accurate prediction of spectral shifts for hydrogen bonded clusters. Another important outcome of this study is about the acceptability of theoretical level for correct prediction of spectral shifting. This study signifies the use of an optimum basis set for a particular system. Any increase in the size of basis set does not guarantee, or might not be necessary for, accurate prediction.

Acknowledgements

The matrix isolation – infrared spectra were recorded in the laboratory of Professor Tapas Chakraborty, Indian Association for the Cultivation of Science. The author thanks Prof. Chakraborty for his assistance.

References

1. G. A. Jeffrey, An Introduction to Hydrogen Bonding, Oxford University Press, New York, 1997.
2. S. Y. Liu, C. E. Dykstra and D. J. Malik, Chem. Phys. Lett., 1986, 130, 403.
3. S. Y. Liu and C. E. Dykstra, Chem. Phys. Lett., 1987, 136, 22.
4. K. J. Hermansson, J. Chem. Phys., 1993, 99, 861.
5. Y. Gu, T. Kar and S. Scheiner, J. Am. Chem. Soc., 1999, 121, 9411.
6. P. Hobza and Z. Havlas, Chem. Rev., 2000, 100, 4253.
7. A. Masunov, J. J. Dannenberg and R. H. Contreras, J. Phys. Chem. A, 2001, 105, 4737.
8. I. V. Alabugin, M. Manoharan, S. Peabody and F. Weinhold, J. Am. Chem. Soc., 2003, 125, 5973.
9. I. V. Alabugin, M. Manoharan and F. A. Weinhold, J. Phys. Chem. A, 2004, 108, 4720.
10. S. A. C. McDowell and A. D. Buckingham, J. Am. Chem. Soc., 2005, 127, 15515.
11. W. Qian and S. Krimm, J. Phys. Chem. A, 2005, 109, 5608.
12. A. Karpfen and E. S. Kryachko, J. Phys. Chem. A, 2005, 109, 8930.
13. J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620.
14. A. D. Buckingham, J. E. del Bene and S. A. C. McDowell, Chem. Phys. Lett., 2008, 463, 1.
15. I. E. Boldeskul, I. F. Tsymbal, E. V. Ryltsev, Z. Latajka and A. J. Barnes, J. Mol. Struct., 1997, 436, 167.
16. W. Caminati, S. Melandri, P. Moreschini and P. G. Favero, Angew. Chem., Int. Ed., 1999, 38, 2924.
17. S. Scheiner, Y. Gu and T. Kar, J. Mol. Struct.: THEOCHEM, 2000, 500, 441.
18. B. J. van der Veken, W. A. Herrebout, R. Szostak, D. N. Shchepkin, Z. Havlas and P. Hobza, J. Am. Chem. Soc., 2001, 123, 12290.
19. X. Li, L. Liu and H. B. Schlegel, J. Am. Chem. Soc., 2002, 124, 9639.
20. S. Scheiner and T. Kar, J. Phys. Chem. A, 2002, 106, 1784.
21. S. M. Melikova, K. S. Rutkowski, P. Rodziewicz and A. Koll, Chem. Phys. Lett., 2002, 352, 301.
22. S. N. Delanoye, W. A. Herrebout and B. J. van der Veken, J. Am. Chem. Soc., 2002, 124, 7490.
23. S. N. Delanoye, W. A. Herrebout and B. J. van der Veken, J. Am. Chem. Soc., 2002, 124, 11854.
24. S. A. C. McDowell, Phys. Chem. Chem. Phys., 2003, 5, 808.
25. A. J. Barnes, J. Mol. Struct., 2004, 704, 3.
26. W. A. Herrebout, S. N. Delanoye and B. J. van der Veken, J. Phys. Chem. A, 2004, 108, 6059.
27. N. Dozova, L. Krim, M. E. Alikhani and N. Lacome, J. Phys. Chem. A, 2005, 109, 10273.
28. K. Pluháčková and P. Hobza, ChemPhysChem, 2007, 8, 1352.
29. A. Mukhopadhyay, M. Mukherjee, P. Pandey, A. K. Samanta, B. Bandyopadhyay and T. Chakraborty, J. Phys. Chem. A, 2009, 113, 3078.
30. A. Mukhopadhyay, P. Pandey and T. Chakraborty, J. Phys. Chem. A, 2010, 114, 5026.
31. P. R. Shirhatti, D. K. Maity, S. Bhattacharyya and S. Wategaonkar, ChemPhysChem, 2014, 15, 109.
32. R. Gopi, N. Ramanathan and K. Sundararajan, J. Phys. Chem. A, 2014, 118, 5529.
33. R. W. F. Bader, Atoms in Molecules. a Quantum Theory, Oxford University Press, Oxford, 1990.
34. P. Pulay and F. Torok, Acta Chim. Acad. Sci. Hung., 1966, 47, 273.
35. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347.
36. Y. Matsumoto and K. Honma, J. Chem. Phys., 2007, 127, 184310.
37. J. Iwamoto, Y. Matsumoto and K. Honma, Chem. Phys., 2013, 419, 184.
38. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
39. A. Gómez-Zavaglia and R. Fausto, J. Phys. Chem. A, 2004, 108, 6953.

---

Footnote

† Electronic supplementary information (ESI) available: Theoretical predictions for optimized geometrical parameters of pyrrole⋯N₂ cluster, N–H stretching frequency of pyrrole, changes in N–H bond length upon H-bond formation and pictorial presentation of bond critical points. See DOI: 10.1039/c5ra17309d

---