Pressure evolution of the potential barriers for transformations of layered BN to dense structures

Abstract

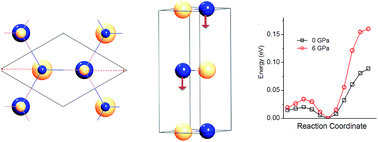
Layered BN is a graphite analogue with exceptionally strong covalent bonding, while dense phases, particularly cubic and wurtzite BN are important hard materials for machine tools and other applications. BN is invariably formed in the layered form and must be converted to the dense phase under pressure. We report the pressure dependent structure of BN and energy barriers for the transformations as a function of initial structure based on first-principles methods including dispersion interactions, which we find to be important. The cohesive energies of the layered structures are similar to that of wurtzite BN. The energy barriers for transformation from rhombohedral layered BN to dense cubic BN and that from hexagonal layered BN to dense wurtzite BN are found to be similar at low pressure. Increasing pressure results in a rapid decrease of these energy barriers. The phase transition from ordered layered structures to the dense phase should be completed at approximately 25 GPa. We find a large energy barrier for layer glides under pressure, which provides an explanation for the difficulty in ambient temperature, high pressure formation of cubic dense BN from layered starting materials that contains stacking faults.

---

Introduction

Boron nitride (BN), which is a carbon analogue, has both layered and cubic phases with thermal, mechanical and electronic properties reflecting extremely strong covalent bonding. The dense cubic phase of BN is a superhard material comparable to diamond. In the synthesis of BN, there are two primary kinds of phases. These are low-density layered-BN with sp² bonding and high-density sp³ phases, similar to carbon. The high-density sp³ bonded phases, in particular cubic BN (c-BN) and wurtzite BN (w-BN), have extremely high hardness with high thermal conductivity, high wear resistance, chemical inertness to ferrous materials and other properties that make them important materials for hard coatings, super-abrasives and tools.^1–4 There are also important differences from carbon, in particular because of the polar bonds. This leads for example to sizable band gaps in the low density phases layered phases in contrast to graphite. The low-density phases such as hexagonal BN (h-BN) and rhombohedral (r-BN) are used as lubricants and may be useful as a dielectric substrate for high mobility graphene transistors.^5–9 Importantly, and also similar to carbon, the low and high density phases of BN are very close in energy, but only the low density phases (graphite and layered BN) are readily made via bulk synthesis at ambient pressure.

The layered phases consist of sp²-bonded planes interacting via weak dispersion interactions and interlayer distances of approximately 3.3 Å. This admits different stacking sequences. Commonly made polymorphs are h-BN, which has AA′ stacking, and r-BN, which has ABC stacking. The dense phases have three-dimensional covalent sp³ networks and include cubic zinc blende structure c-BN and wurtzite structure w-BN, both of which are widely used in applications. Not surprisingly, the properties of the layered and dense phases are very different. As mentioned, only the layered phases are readily formed at ambient pressure and so understanding the transformations between the layered and dense phases is important and has attracted much attention.^10–22 It has been long held that h-BN is the lowest energy structure of BN at ambient pressure, similar to carbon, where graphite is the ground state, and that the denser sp³ bonded structures become stable under pressure,¹² but this is less well established for BN than for carbon, and there is data suggesting that c-BN could be lower in energy.^23–25 In any case, while the energy difference between the lowest energy layered and dense phases, h-BN and c-BN, is very small.

The transformation to the dense phases is controlled by an energy barrier, which can be overcome by pressure and is more easily overcome using pressure in combination with high temperature and catalysts.^10,11 Highly-ordered h-BN is easily transformed to w-BN at pressures of 8.1–13 GPa.^12–16 The lowest pressure at which the transformation starts at room temperature is 8.1 GPa. This transformation from highly-ordered h-BN to w-BN is reported to be complete under 25 GPa.¹⁵ Interestingly, the needed pressure drastically increases as the layer stacking disorder in the starting material increases and in fact there is no reported high pressure formation of w-BN or c-BN from layered BN with disordered stacking sequences (turbostratic phases) at room temperature. Also it is notable that a direct transition from r-BN to c-BN was observed in shock experiments with pressures higher than 40 GPa and temperatures above 1000 K.^26,27 w-BN for super-abrasives is commonly made by a detonation method. This paper addresses the energy barrier, its evolution with pressure and the role of stacking in the starting material. However, first we briefly discuss the issue of the true ground state of BN.

As mentioned, the stable allotrope found in ambient pressure synthesis is h-BN,²⁸ while c-BN can be synthesized under high pressure and w-BN is metastable under usual growth conditions. Therefore, h-BN is traditionally considered to be the ground state of BN.¹² However, recent experimental measurements of Solozhenko et al. suggest that the ground state may be c-BN.^23–25 A number of first principles calculations of the energetics have been reported.^29–37 With the local density approximation (LDA) the total energy of c-BN is lower than that of h-BN.^29,30,33,38 For example, Kern et al. conducted a study of stability of c-BN and h-BN with the analysis of lattice dynamics and found that c-BN can be stable up to about 1400 K under zero pressure.^30,33,38 Janotti et al. performed all electron LDA and generalized gradient approximation (GGA) calculations.³⁹ They found that LDA predicted dense cubic structures as the ground states and that standard GGA calculations gave opposite result. Also, the lack of dispersion interactions in the GGA resulted in a very large c-axis lattice parameter for h-BN with the implication that addition of dispersion interactions to GGA calculations is critical at least for the layered phases. Halo et al. found that electron correlation has an important effect on the relative stability of cubic and hexagonal polymorphs of BN.⁴⁰ They found that Hartree–Fock (HF) underbinds both phases and energetically favors h-BN and that correlation changes the order. Clearly, the relative stability is still an open question.

Here we use GGA calculations with addition of a dispersion interaction. This is motivated by the fact that for solids, GGA calculations generally give better cohesive energies as compared to the LDA, and literature results implying that the inclusion of dispersion interactions is important in BN. We find, as may be expected, that inclusion of dispersion interactions decreases the c-axis lattice parameter of h-BN improving agreement with experiment and confirming their importance. With dispersion interactions, we obtain c-BN as the ground state, and find that w-BN and h-BN have very similar cohesive energies.

We now turn to the main subject of this paper, i.e. the barrier against transformation from layered to dense phases. Wentzcovitch et al. studied the transition paths from h-BN to w-BN and from r-BN to c-BN.³⁵ Furthműller et al. also studied the transition between layered phases and dense phases with a pathway consisting of buckling of the honeycomb layers,³¹ while more complicated pathways were considered by Yu et al.⁴¹ Hromadova et al. used metadynamics simulations over an extended temperature range of 300 to 3000 K using the LDA and found that there is direct transition from layered r-BN to c-BN,⁴² while the usual allotrope h-BN was found to transform to w-BN at temperatures below 700 K. Here, we studied the barriers for phase transformation from layered structures to c-BN and w-BN under different pressures using dispersion corrected GGA calculations. We also analyzed the possibility of relative layer motions in layered structures, which is relevant to understanding the difficulty in producing the transformation to c-BN under pressure at ambient temperature.

Computational method

The present calculations are performed within density functional theory using accurate frozen-core full-potential projector augmented-wave (PAW) pseudopotentials, as implemented in the VASP code.^43–45 We did calculations with the local density approximation (LDA),⁴⁶ the generalized gradient approximation (GGA) of Perdew, Burke and Ernzerhof (PBE)^47,48 and the PBE GGA with added van der Waals (vdW) corrections.^49–51 In order to compare with the PBE, we check the other GGA functionals, including RPBE and TPSS.⁵² Besides the D2 of Grimme, we also use the D3 method with Becke–Jonson damping to analyze the effect of vdW interactions.⁵³ In addition, we consider the hybrid functional by using the HSE06 (ref. 54).

The zinc blende (F4̄3m) structure of c-BN along with the other structures including w-BN (P6₃mc), r-BN (R3m) and h-BN (P6₃/mmc) are shown in Fig. 1. The k-space integrals and the plane-wave basis sets are chosen to ensure that the total energy is converged at 1 meV per atom level. A kinetic energy cutoff of 500 eV for the plane wave expansion is found to be sufficient. The Brillouin zones are sampled with dense Γ-centered 18 × 18 × 10 grids (note that we used a non-primitive cell as shown in Fig. 1 for c-BN to keep on the same footing as the other phases, particularly w-BN). The method for applying pressure in the present calculations was to add external stress to stress tensor in VASP code, and the structure of bulk BN with different phases was then optimized under the specified hydrostatic pressure. We analyzed the energy barriers for transformations between the different phases for pressures up to 32 GPa.

Fig. 1 Crystal structure of BN in the hexagonal phase h-BN (a), the wurtzite phase w-BN (b), the layered rhombohedral phase r-BN (c) and the cubic zinc-blende phase c-BN (d).

Results and discussion

1. The ground state of BN

Table 1 presents the calculated lattice parameters a, c/a, volume V and cohesive energy E_c. The calculated results are compared with previous LDA and GGA calculations and available experimental data. The LDA results are consistent with previous LDA calculations and are in reasonably good agreement with experiment. The equilibrium volumes are underestimated slightly by LDA. The volumes of c-BN and w-BN are similar. The volumes of layered structures, such as h-BN and r-BN are much larger than that of dense phases including c-BN and w-BN. The LDA predicts that c-BN is the ground state. The total energy of w-BN is 18 meV per atom above that of c-BN. h-BN and r-BN are similar to each other and approximately 60 meV per atom higher than c-BN.

Table 1 Calculated equilibrium structural parameters and cohesive energies of BN with LDA, PBE/GGA, RPBE/GGA, TPSS/GGA, HSE06, PBE + D2 and PBE + D3 with Becke–Jonson damping. Results are compared with available experiment data (ref. 17–22, 29 and 33). Note that PBE + D2 and PBE + D3 with Becke–Jonson damping are the PBE/GGA with dispersion interactions and the volumes are calculated by the lattice parameters from DFT

	LDA	PBE/GGA	RPBE/GGA	TPSS/GGA	HSE06	PBE + D2	PBE + D3	Expt.
c-BN
V (Å^3 per atom)	5.748	5.959	6.024	5.949	5.954	5.895	5.866	5.905
a	3.583	3.626	3.639	3.624	3.625	3.613	3.607	3.615
Ec (eV per atom)	6.551	5.300	4.530	6.900	2.717	5.549	5.509	6.6
w-BN
V (Å^3 per atom)	5.765	5.973	6.040	5.973	5.837	5.903	5.882	5.966
a	2.525	2.555	2.565	2.555	2.536	2.545	2.542	2.553
c/a	1.654	1.654	1.653	1.654	1.653	1.654	1.654	1.656
Ec (eV per atom)	6.533	5.283	4.513	6.883	2.702	5.524	5.491
h-BN
V (Å^3 per atom)	8.850	10.059	10.159	10.188	10.011	8.422	8.886	9.042
a	2.489	2.512	2.522	2.517	2.497	2.509	2.506	2.504
c/a	2.651	2.931	2.925	2.951	2.970	2.463	2.608	2.660
Ec (eV per atom)	6.491	5.375	4.646	6.948	2.760	5.520	5.505
r-BN
V (Å^3 per atom)	8.898	10.193	10.969	10.227	10.082	8.317	8.883	9.045
a	2.491	2.512	2.521	2.514	2.497	2.508	2.506	2.504
2c/3a	2.659	2.970	3.162	2.973	2.991	2.435	2.607	2.661
Ec (eV per atom)	6.493	5.375	4.651	6.949	2.760	5.521	5.505

---

The lattice parameters and volume calculated by PBE/GGA are similar to that of Janotti et al. with full electron GGA.³⁹ The interlayer attraction due to dispersion interactions is essentially missing from the PBE GGA. Relative to the LDA, the PBE/GGA increases the lattice parameters, especially lattice constant c to very large values corresponding to unbound layers. The PBE/GGA predicts the c/a ratio for layered structures is drastically larger than the experimental value of 2.66. The other two common used functionals, RPBE and TPSS give the similar results about the lattice parameters, compared with that of PBE. In addition, the hybrid functional is checked by using the HSE06 functional. It also predicts the high c/a ratio for layered structures, compared with the experimental results. Obviously, the screened hybrid functional can't incorporate effectively the vdW interaction, though it can correct properly the band gap of usual semiconductors. The improper consideration of long-range interaction in common used GGA and hybrid functional results in the improper increase of distance between layers.

With the results of LDA and GGA, the energy difference from different layered structures is very small. Therefore, the stacking sequence plays a very minor role in the cohesive energy. Importantly, the GGA results predict that the layered structures are more stable than the c-BN, opposite to the LDA. It is also noticed that the cohesive energies given by different functionals are very different. By compared with the experimental value of c-BN, the cohesive energies from LDA, PBE, RPBE and HSE06 are smaller and that from TPSS is larger. While the values of HSE06 are far away from the experimental value, that from LDA and TPSS are close to the experimental value.

With vdW correction, the layers are bound and the c/a ratio is reduced. The cohesive energies are also increased properly from the results of PBE + D2 and PBE + D3 with Becke–Jonson damping. At the same time the ground state is switched to c-BN, with energy 29 meV per atom below the layered structures from PBE + D2. The cohesive energy of w-BN is just a little larger than that of layered structures. From PBE + D3 with Becke–Jonson damping, the energy of c-BN is about 4 meV per atom lower than that of layered structures. The cohesive energy of layered structures is a little larger than that of w-BN. For the calculated the lattice parameters, the c/a ratio from PBE + D3 is more close to the experimental values for layered structures. The cohesive energies of dense and layered structures are similar.

Fig. 2 shows the pressure dependence of the enthalpies. The enthalpy difference between w-BN and c-BN does not change substantially with pressure and c-BN is always lower. The enthalpies of layered structures h-BN and r-BN are similar for the pressures studied. However, with the increase of pressure, the enthalpy difference between layered structures and dense phases becomes larger as expected.

Fig. 2 Calculated enthalpies of w-BN, c-BN, h-BN and c-BN (a), relative lattice parameters a/a₀ (b), c/c₀ (c) and relative volumes V/V₀ (d) as a function of pressure. The lattice parameters and volumes are referenced to their equilibrium values under zero pressure (corresponding to 1.00).

2. Barrier for phase transformation

The transition from the hexagonal phase h-BN to w-BN can be computationally described by considering a 4-atom unit cell with a pair of N atoms with internal coordinates (1/3, 1/3, 0) and (1/3, 2/3, 0.5) moving down (see Fig. 1) or equivalently a pair of B atoms moving up along the z direction. Similarly, a conventional cell of c-BN can be transformed into the hexagonal form. As shown in Fig. 1c, the N atoms or/and B atoms stack in an ABC pattern. Moving three N atoms down or equivalently three B atoms up along the z direction, as shown, results in the transformation of r-BN to c-BN. To model this, the whole cell including the lattice parameters needs to be relaxed while the internal coordinates of atoms change in the cell. These then describe continuous transformation paths from h-BN to w-BN and from r-BN to c-BN, obtained by buckling of the hexagonal BN layers. This is similar to or equivalent to the descriptions given in prior work.^31,35

We find that, if one starts with one of the layered structures (r-BN or h-BN), the energy increases as the buckling of the layers starts and at the same time the c/a ratio rapidly decreases reflecting an increase in the interlayer interaction, as shown in Fig. 3–5 and discussed below. This leads to a sharp decrease in the volume. This decrease in c/a becomes much weaker beyond the saddle point (the energy maximum along the transformation path). This is similar to the description in the earlier work.^31,35 Importantly, calculations without dispersion interactions predict that the energy barrier from r-BN to c-BN is 0.22 eV per atom and that from h-BN to w-BN is 0.26 eV per atom at 0.4 GPa, but with the dispersion interactions we find that the barrier from r-BN to c-BN is substantially lower. We obtain 0.16 eV per atom for the barrier and also a lower barrier of 0.18 eV per atom for h-BN to w-BN at this pressure by PBE + D2 method. Interestingly, the energy barrier from r-BN to c-BN calculated with the PBE GGA including dispersion interactions is similar to the LDA result of Furthműller et al.³¹

Fig. 3 Variation of the total energy from the layered structure r-BN to c-BN following the degree of buckling of the hexagonal layers for different pressures as calculated with PBE/GGA (a) and energy barrier as the pressure calculated by PBE/GGA with and without dispersion interactions (b). Note that the total energy is given to be relative to the total energy of r-BN at zero pressure and the barrier energy is calculated with a six atom unit cell. Note that the dispersion interactions are considered with PBE + D2 method.

Fig. 4 Variation of the total energy from the layered structure h-BN to w-BN following the degree of buckling of the hexagonal layers for different pressures calculated by PBE/GGA (a) and energy barrier as the pressure calculated by PBE/GGA with and without dispersion interactions (b). Note that the total energy is given to be relative to the total energy of h-BN at zero pressure and the barrier energy is calculated with a unit cell of 4 atoms. Note that the dispersion interactions are considered with PBE + D2 method.

Fig. 5 Schematic representation of a unit cell of hexagonal BN with 2-layer structure by AB stacking (a) and AA stacking (c), and the variation of total energy per 4-atom along the path indicated by the arrow in (a) under 0 pressure and 6 GPa (b) and that along the path indicated by the arrow in (c) under 0 pressure and 6 GPa (d).

The barriers from h-BN to w-BN at 0.4 GPa by PBE + D2 method (0.18 eV per atom) and PBE + D3 method (0.199 eV per atom) are a little larger than the LDA result (0.17 eV per atom). In order to explore the effect of the layer's distance in the initial structure on the energy barrier, we calculated the energy barrier by GGA PBE with the structures from PBE + D2 minimum/transition state. The value is about 0.245 eV per atom and is larger than the PBE + D2 result and less than the direct PBE result. We also perform the calculations of energy barrier by hybrid functional HSE06 with the PBE + D2 minimum/transition state geometries. The result (0.243 eV per atom) is similar to that from PBE GGA. Therefore, the effect of layers' distance in the initial structure is less important than that in the structure of transition state since the layers' interaction in the initial structure is weak. The consideration of dispersion interaction at transition state is important to analyze the energy barrier.

The c lattice parameter of the layered phases is much more sensitive to pressure than the in-plane a lattice parameter as may be expected. This increases the tendency for interlayer bonding and layer buckling. As shown in Fig. 3 and 4, the energy barriers decrease rapidly with pressure. Furthermore, the dispersion interactions substantially decrease the energy barrier for all pressures studied. At 25 GPa, the energy barrier from r-BN to c-BN is approximately 21 meV per atom with the dispersion interactions, while the energy barrier from h-BN to w-BN is approximately 31 meV per atom by PBE + D2 method. These low barriers mean that both phase transformations can readily occur around 25 GPa. In addition, it would appear that the phase transition from r-BN to c-BN is easier than that from h-BN to w-BN. However, experiments indicate that the transformation of layered structures to the c-BN phase is more difficult than that to w-BN at least at low pressure.

Turning to the layer stacking, there are two basic types of stacking of the hexagonal layers of BN. One is where B and N atoms of second layer are positioned relative to the B and N atoms of first layer by translation in Fig. 5a and the other has the B and N atoms of second layer related to those of first layer as shown in Fig. 5c. These structures can be transformed into each other by rotating the second layer 60° along z axis. For the first type of stacking (Fig. 5a), there are two energy minima on the potential energy surface for the relative gliding of the layers, as shown in Fig. 5b. The two energy minima correspond to the AB and AC stacking. There is a large energy barrier for the transformation between the structures by this glide (Fig. 5b). In addition, the energy barrier increases with pressure reflecting the increasing of interlayer interactions under pressure. Therefore, for the transition from a layered structure to c-BN under pressure, the layered structure must have ABC stacking. However, the stacking fault energy is very low in this type of structure since faults can have zero energy with only nearest layer interactions, similar to stacking faults in graphite. However, an AB or AC stacking fragment will not be easily transformed into the stable dense phase at low pressure. For the second type of stacking, there is just one energy minima with the configuration in Fig. 5c. There is also one metastable configuration with the B atom of second layer related to the B site of first layer by translation along the path in Fig. 5c. The energy barrier around the minima increases with pressure. Therefore, layered BN with this second type of stacking can be readily transformed to w-BN under pressure.

Conclusions

We report a first principles study of the ground state of BN and the phase transitions from layered structures to dense phases. We find that dispersion interactions are important effect both for the phase stability and for the barriers for transformation to the dense phases. With the PBE GGA and dispersion interactions we find the ground state to be the c-BN phase. At low pressure, the energy barriers for transformation from r-BN to c-BN and from h-BN to w-BN are similar. In both cases the barriers of decrease quickly with pressure. The fact that the w-BN phase forms more readily than the c-BN phase by cold-compression of layered structures may be understood in terms of the effect of stacking in the starting layered materials.

References

1. S. Veprek, J. Vac. Sci. Technol., A, 1999, 17, 2401.
2. G. Bobrovnitchii and M. Filgueira, J. Mater. Process. Technol., 2005, 170, 254.
3. Z. Pan, H. Sun, Y. Zhang and C. Chen, Phys. Rev. Lett., 2009, 102, 055503.
4. Y. Tian, et al., Nature, 2013, 493, 385.
5. G. Giovannetti, P. A. Khomyakov, G. Brocks, P. J. Kelly and J. van den Brink, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073103.
6. C. R. Dean, et al., Nat. Nanotechnol., 2010, 5, 722.
7. A. Pakdel, Y. Bando and D. Golberg, Chem. Soc. Rev., 2014, 43, 934.
8. X. Fan, Z. Shen, A. Q. Liu and J.-L. Kuo, Nanoscale, 2012, 4, 2157.
9. L. Ci, et al., Nat. Mater., 2010, 9, 430.
10. T. Sekine and T. Sato, J. Appl. Phys., 1993, 74, 2440.
11. V. F. Britun, A. V. Kurdyumov, N. I. Borimchuk, V. V. Yarosh and A. I. Danilenko, Diamond Relat. Mater., 2007, 16, 267.
12. F. R. Corrigan and F. P. Bundy, J. Chem. Phys., 1975, 63, 3812.
13. T. Taniguchi, T. Sato, W. Utsumi, T. Kikegawa and O. Shimomura, Appl. Phys. Lett., 1997, 70, 2392.
14. F. P. Bundy and R. H. Wentorf, J. Chem. Phys., 1963, 38, 1144.
15. V. L. Solozhenko and F. Elf, J. Superhard Mater., 1998, 20, 62.
16. L. Liu, Y. P. Feng and Z. X. Shen, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 104102.
17. R. W. Lynch and H. G. Drickamer, J. Chem. Phys., 1966, 44, 181.
18. V. L. Solozhenko, Thermochim. Acta, 1993, 218, 221.
19. V. L. Solozhenko, Diamond Relat. Mater., 1994, 4, 1.
20. V. L. Solozhenko, G. Will, H. Hupen and F. Elf, Solid State Commun., 1994, 90, 65.
21. M. Grimsditch, E. S. Zouboulis and A. Polian, J. Appl. Phys., 1994, 76, 832.
22. P. K. Lam, R. M. Wentzcovitch, and M. L. Cohen, in Materials Science Forum, ed. J. J. Pouch and S. A. Alterovitz, Trans Tech Publications, Zurich, Switzerland, 1990, Vol. 54 and 55.
23. S. Bohr, R. Haubner and B. Lux, Diamond Relat. Mater., 1995, 4, 714.
24. V. L. Solozhenko, J. Hard Mater., 1995, 6, 51.
25. H. Sachdev, R. Haubner, H. Noth and B. Lux, Diamond Relat. Mater., 1997, 6, 286.
26. T. Sato, T. Ishii and N. Setaka, J. Am. Ceram. Soc., 1982, 65, c162.
27. A. V. Kurdyumov, V. F. Britun and I. A. Petrusha, Diamond Relat. Mater., 1996, 5, 1229.
28. L. I. Berge, Semiconductor Materials, CRC Press, NewYork, 1997.
29. K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 6203.
30. G. Kern, G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8551.
31. J. Furthműller, J. Hafner and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 15606.
32. Y.-N. Xu and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7787.
33. E. Knittle, R. M. Wentzcovitch, R. Jeanloz and M. L. Cohen, Nature, 1989, 337, 349.
34. R. M. Wentzcovitch, K. J. Chang and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 1071.
35. R. M. Wentzcovitch, S. Fahy, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 6191.
36. N. Ohba, K. Miwa, N. Nagasako and A. Fukumoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 115207.
37. K. Shirai, H. Fujita and H. Katayama-Yoshida, Phys. Status Solidi B, 2003, 235, 526.
38. H. Chacham and L. Kleinman, Phys. Rev. Lett., 2000, 85, 4904.
39. A. Janotti, S. H. Wei and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174107.
40. M. Halo, C. Pisani, L. Maschio, S. Casassa, M. Schutz and D. Usvyat, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035117.
41. W. J. Yu, W. M. Lau, S. P. Chan, Z. F. Liu and Q. Q. Zheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 014108.
42. L. Hromadova and R. Martonak, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 224108.
43. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
44. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
45. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
46. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048.
47. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
49. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
50. X. F. Fan, W. T. Zheng, V. Chihaia, Z. X. Shen and J.-L. Kuo, J. Phys.: Condens. Matter, 2012, 24, 305004.
51. G. Mercurio, et al., Phys. Rev. Lett., 2010, 104, 036102.
52. J. Sun, M. Marsman, G. Csonka, A. Ruzsinszky, P. Hao, Y.-S. Kim, G. Kresse and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035117.
53. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
54. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.

---