Experimental and theoretical study on thermal decomposition of methyl butanoate behind reflected shock waves†
Abstract
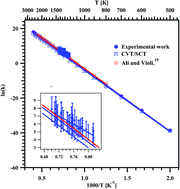
Thermal decomposition of methyl butanoate (MB) diluted in argon was studied behind reflected shock waves in the temperature range of 1229–1427 K using a single pulse shock tube (SPST). The post shock mixtures were analyzed quantitatively using gas chromatography (GC) and qualitatively using Fourier-transform infrared (FTIR) spectroscopy. Methane (CH4), ethylene (C2H4), and acetylene (C2H2) were the major decomposition products. The minor products are ethane (C2H6), propylene (C3H6), 1,3-butadiene (C4H6) and methyl acrylate (C4H6O2). The obtained first order rate coefficient for the decomposition of MB is ktotal (1229–1427 K) = (3.08 ± 1.11) × 1012 exp(−(53.6 kcal mol−1 ± 4.7)/RT) s−1, and for the formation of C2H4, the rate coefficient was found to be kethylene (1229–1427 K) = (7.92 ± 2.72) × 109 exp(−(47.6 kcal mol−1 ± 4.5)/RT) s−1. Theoretical kinetic calculations were also performed for the unimolecular hydrogen transfer reactions using canonical variational transition state theory (CVT) with small-curvature tunneling (SCT) corrections. The temperature dependent rate coefficients for the overall reaction were computed in the temperature range of 500–2500 K, and were used to derive the Arrhenius expression: ktheorytotal (500–2500 K) = (9.05 ± 1.91) × 1013 exp(−(70.7 kcal mol−1 ± 2.0)/RT) s−1. A reaction scheme containing 39 species and 66 elementary reactions was proposed to simulate the reactant and product concentrations over the temperature range of 1229–1427 K. The agreement between the experimental results and the model prediction for all the species is observed to be good. The decomposition of MB happens mostly via intramolecular hydrogen transfer than C–C bond and C–O bond fission. The majority of these intramolecular hydrogen transfer reactions are lower energy barrier reactions than the homolytic bond fission reactions.

 Please wait while we load your content...
Please wait while we load your content...