Origin of the highly anisotropic thermal expansion of the semiconducting ZnSb and relations with its thermoelectric applications†
Abstract
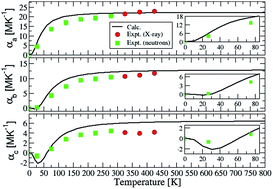
This article is devoted to the thermal expansion of ZnSb combining experiments (neutron and X-ray) and calculations based on density functional theory. Related properties are also studied such as: the zone-center (Raman and infrared) phonon modes, the dielectric (electronic and static) tensors, the phonon density-of-states, the specific heats and the isotropic atomic displacement parameters. Our experimental data show highly anisotropic thermal expansion with large values along the a-direction. Concomitantly, a large increase of the Zn–Zn intra-ring distances and of one of the intra-ring Zn–Sb distances is observed, while other interatomic distances do not significantly change. In agreement with our calculations, the thermal expansion has positive values along the three crystal directions except around 30 K where it has weak negative values along the b and c-directions. This anomalous expansion is more important along the c-direction and it is mainly due to phonon modes with frequencies up to 75 cm−1. These modes are located in the S–Y–Γ (resp. Γ–Z) q-point range along the b (resp. c) direction. Phonon modes located in the Γ–X and in the Y–Γ–Z q-point range with frequencies up to 175 cm−1 are responsible for the positive large thermal expansion at room temperature along the a-direction. The much reduced anisotropy of the thermal conductivity is related to the lower Debye temperatures along the b and c-directions and mainly to the small transverse sound velocity between these directions.

 Please wait while we load your content...
Please wait while we load your content...