Rheology, thermal properties, and foaming behavior of high d-content polylactic acid/cellulose nanofiber composites
Abstract
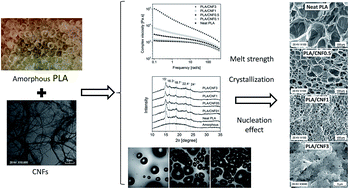
Amorphous polylactic acid (PLA)/cellulose nanofiber (CNF) composites were prepared using the solution casting method. We investigated the effects of the CNFs on the PLA's rheological and thermal properties and on its foaming behavior. The rheological measurements showed that the incorporated CNFs substantially increased the PLA's viscosity in a low frequency range. This was attributed to both the interaction between the PLA molecular chains and the CNFs and the entanglement of CNFs. A batch foaming visualization system showed that the CNFs were effective cell-nucleating agents, and that they suppressed cell coalescence during the foaming process. In solid-state batch foaming processes, the addition of CNFs led to higher cell densities and decreased cell sizes in the composite foams. As the CNF content was increased, the cell-nucleating power and the resultant cell density increased. The cell sizes became more uniform. The improved foam morphology was also attributed to the CO2- and the CNF-induced crystallization during the gas-saturation and foaming processes. Thermal and wide angle X-ray diffraction (WAXD) analyses showed that the presence of CNFs and CO2 enhanced the PLA's crystallization kinetics. An amorphous grade of PLA with a 12% D-content developed a high crystallinity of 21% after CO2 gas saturation. The formed crystals, especially those around the CNFs, promoted cell nucleation by local stress variations that were generated in the surrounding area. The crystals and CNFs also increased the PLA's viscosity, which restricted cell growth and reduced cell coalescence. On the other hand, due to increased stiffness, an excessive CNF content suppressed foaming.

 Please wait while we load your content...
Please wait while we load your content...