Strain-induced semimetal-to-semiconductor transition and indirect-to-direct band gap transition in monolayer 1T-TiS₂

Abstract

We have investigated the effect of uniform plane strain on the electronic properties of monolayer 1T-TiS₂ using first-principles calculations. In the absence of strain, we find monolayer TiS₂ is a semimetal, with a small overlap of the valence band maximum and the conduction band minimum. The band overlap increases under compression; however under tensile, monolayer 1T-TiS₂ experiences a transition from a semimetal to a semiconductor as a band gap emerges. Moreover, the electronic properties change from an indirect to a direct band gap upon application of greater tensile strain. Thus one can modulate the properties of monolayer TiS₂ by applying the appropriate strain, thereby providing a route towards control in optoelectronic devices.

---

Transition metal disulfides crystallize in layered forms. Within each layer, metal and sulfur atoms are held together by strong bonding interactions such that the metal atomic plane is sandwiched between two sulfur atomic planes. Normal to the planes, the individual layers are bound by weak van der Waals forces. These layers can be separated to form two-dimensional crystals composed of one to several layers by various synthetic routes.^1–3 Among the transition metal sulfides, TiS₂ is of particular interest due to its intriguing electronic, structural, and optical properties.^4,5 Moreover, these properties facilitate a synergistic coupling to other materials that has been reported to improve electro- and photocatalytic activity of hydrogen evolution reactions.^6,7

It is well known that strain can modulate the band structure of low dimensional materials. For example, monolayer MoX₂ (X = S, Se, and Te) experiences an indirect-to-direct band gap transition and a semiconductor-to-metal transition under mechanical strain due to the relocation of the conduction band minimum.⁸ In this letter, we present a density functional theory investigation on monolayer TiS₂ under strain and report equally drastic changes to its electronic properties. Upon increasing tensile strain, the material evolves from a semimetal into a small band gap semiconductor. Concurrently, we observe a transition in the band gap from indirect to direct (and then back to indirect). This provides a way to tune the electronic properties of monolayer TiS₂ in a precise fashion by controlling the extent of strain on the monolayer.

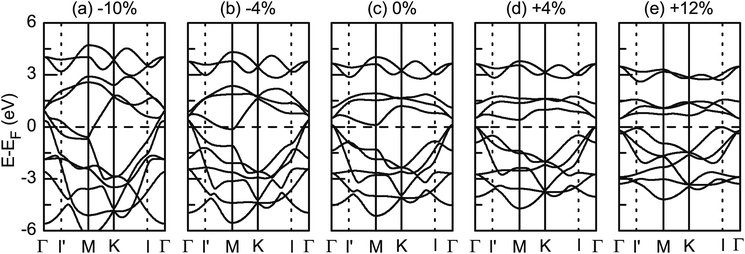
We begin by presenting the properties of unstrained monolayer TiS₂. It consists of three atomic layers, where the titanium layer is sandwiched between two sulfur layers. TiS₂ favors the 1T structure, as opposed to the 2H structure (see Fig. 1). We have compared the energies of monolayer TiS₂ in the 2H and 1T phases, and find 1T-TiS₂ is 0.142 eV per atom lower in energy. All results from this point forward are on the 1-T phase. Fig. 2c and 3b show the band structure and density of states (DOS) of monolayer TiS₂. The primary feature is the Fermi energy (E_F) crosses the valence and conduction bands. The valence band maximum (VBM) is located at Γ 0.109 eV above E_F, while the conduction band minimum (CBM) is located at M 0.104 eV above E_F. As observed from the relative position of the VBM and CBM, there is an energetic overlap of 5 meV suggesting the semimetallic nature of monolayer TiS₂. The angular moment resolved DOS of monolayer TiS₂ can be divided into four main groups with respect to their energies. The first group between −13.6 and −11.9 eV mainly stems from the s states of sulfur and has a sharp peak at −11.91 eV. These states lie far below E_F and have little influence on the properties of monolayer TiS₂. The second group lies between −5.2 eV and E_F, and consists primarily of S-p states and to a lesser extent Ti-d. The third group is located between E_F and 1.8 eV, including hybridization between mainly Ti-d states with some S-p states. The second and third groups meet at E_F, where an inversion of their primary character occurs. The fourth group lies between 2.6 and 3.9 eV, and the hybridization is similar to that of the third group.

Fig. 1 Schematic structure of 1T- and 2H-TiS₂. The 1T phase is 0.142 eV per atom lower in energy.

Fig. 2 Band structures of monolayer 1T-TiS₂ under strain. Panels (a)–(e) correspond to strains of −10%, −4%, 0%, +4%, and +12%, respectively. The Fermi energy is denoted by a horizontal dashed line at zero energy. The I′ and I points in the first Brillouin zone marked by dotted lines are not points with high symmetry.

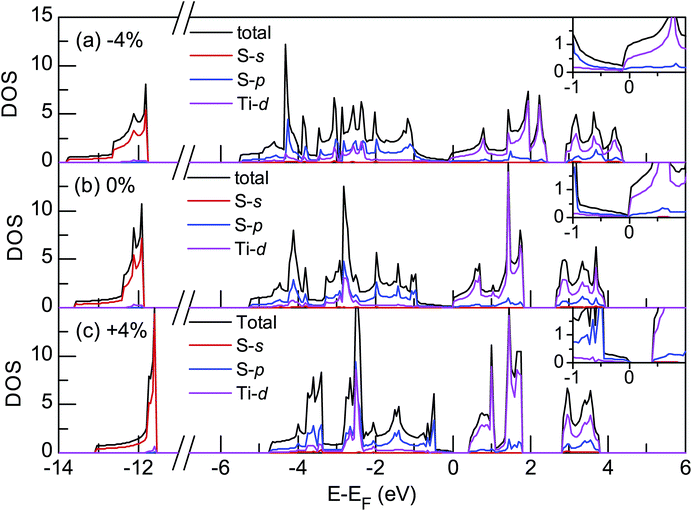Fig. 3 Density of states of monolayer 1T-TiS₂ under strain. Panels (a–c) are under −4%, 0%, and +4% strain, respectively. The insets show the DOS near E_F.

Since the DOS and energy overlap at E_F is quite small (Fig. 2c and 3b), a slight disturbance in the structure may alter the electronic properties substantially. Indeed, strain on other two-dimensional materials – such as graphene,⁹ 2H-MoS₂,^10,11 and ZrS₂,¹² – can adjust the relative position of the valence and conduction band edges. We have calculated the case of compression (negative strain) and tensile (positive strain) of monolayer TiS₂. Under slight compression (−4%, Fig. 2b), the VBM at Γ is shifted up while the CBM at M is shifted down with respect to E_F. The corresponding DOS at −4% strain is not altered in hybridization components, but the four groups are broadened energetically. Most notably, the second and third groups expand into each other's energy range near E_F. As a result, the overlap of conduction and valence bands is enlarged, making monolayer TiS₂ more semimetallic. Increasing compression further shifts the lowest conduction band at the Γ point down. As a consequence, the conduction and valence bands at Γ get closer as compression increases and finally converge energetically when compression is −8%. At this point, the material can be understood as a metal, as part of the original conduction and valence bands are degenerate (Fig. 2a).

We have investigated the geometric variations and charge transfer in strained monolayer TiS₂ to further understand the effects of strain on this material. The results are presented in Table 1. Under compression, the distance between Ti and S atoms is shortened while fewer electrons are transferred from Ti to S, implying covalent bonding is increasing more rapidly than ionic attraction. Compared to zero strain, there is a redistribution of electrons from S_3p states towards Ti_4d, which is shown in the DOS as an expansion of the third group (mainly Ti_4d state) into the range of the second group (largely S_3p state). As a consequence, the second group and third group in the DOS merge into each other. In the corresponding band structure, this is manifested as more overlap of valence and conduction bands.

Table 1 The effect of strain on the geometry and band gap of monolayer 1T-TiS₂. The complete data set is provided in the ESI. Negative (positive) strain means compression (tensile). d_Ti–S is the bond length between nearest Ti and S atoms, h_S–S represents the interlayer height between upper and lower S atomic planes, and CT means charge transfer from Ti to S atoms. Negative band gap indicates overlapping of valence and conduction bands. VB–CB denotes the transition point from valence to conduction bands, and ind/dir refers to whether the transition of VB–CB is indirect or direct

Strain (%)	dTi–S (Å)	hS–S (Å)	CT (e)	Band gap (eV)	VB–CB	Ind/dir
−10	2.368	3.150	1.528	—	—	—
−8	2.378	3.091	1.566	—	—	—
−4	2.400	2.968	1.639	−0.521	Γ–M	Ind
0	2.427	2.851	1.702	−0.005	Γ–M	Ind
+4	2.459	2.737	1.741	0.401	Γ–M	Ind
+6	2.476	2.677	1.752	0.567	Γ–Γ	Dir
+9	2.500	2.581	1.769	0.641	Γ–Γ	Dir
+10	2.508	2.547	1.771	0.601	I–Γ	Ind
+15	2.548	2.354	1.778	0.431	I–Γ	Ind
+20	2.586	2.125	1.768	0.389	I–Γ	Ind

---

When a positive strain, or tensile, is applied to monolayer TiS₂, the VBM and CBM are shifted away from each other energetically as shown in Fig. 2d and e. The band structure for +4% strain displays the features of an indirect band gap semiconductor. In this case, the VBM and CBM are still located at Γ and M points, respectively; however, the energetic overlap has disappeared because the conduction bands are shifted upward. The corresponding DOS (Fig. 3c) is again very similar to the others in component and hybridization. However under +4% strain, the energy distribution of each of the four groups is narrower and the overall range is condensed. Also, the second and third groups are now separated from each other, and the conduction band no longer crosses E_F. So we see an energy gap emerges, and a semimetal-to-semiconductor transition occurs under tensile. As shown in Fig. 2d, the Γ and M points of the lowest conduction band are shifted upward at different rates in response to strain, with Γ shifting slower than M. Consequently, the CBM moves from M to Γ as the tensile strain reaches +6%, resulting in a direct band gap of 0.567 eV. Therefore, the semiconductor type changes from an indirect to direct band gap. Tensile also disproportionately affects the energetics of the valence bands. As the strain increases from 0%, two new points I′ (about 39% from Γ to M) and I (about 34% from Γ to K) are shifted upward in energy rapidly, with I being higher. When strain reaches +10%, the I point exceeds the Γ point to become the VBM, while the CBM remains at the Γ point. Consequently, monolayer TiS₂ changes from a direct band gap (Γ → Γ) to an indirect gap (I → Γ), as shown in Fig. 2e for +12% strain. To summarize the effect of strain, we find monolayer TiS₂ is a semimetal under compression, an indirect semiconductor when strain is between 0 and +6% as well as above +10%, and a direct semiconductor when strain is in the range from +6% to +10%.

Contrary to compression, TiS₂ under tensile strain has extended Ti–S bonds and more electron transfer (Table 1), suggesting ionic attraction plays a more important role. In this way, electrons are localized around atoms to a greater degree and become less itinerant. Therefore, the separation between the valence and conduction bands is enlarged. The energetic overlap is removed and a band gap appears. The band gap increases with strain until it reaches a maximum of 0.641 eV at +9% tensile. This is accompanied by an increase in charge transfer. Beyond this strain the band gap decreases, and charge transfer oscillates slightly while generally trending down. When strain is larger than +16%, the band gap remains almost constant in the range between 0.383 eV and 0.389 eV.

In summary, we have investigated the effect of strain on the electronic properties of monolayer 1T-TiS₂. We find the monolayer is a semimetal in the absence of strain. The semimetallic nature increases with compression and is accompanied by more overlap of the valence and conduction bands. Under tensile, however, the energetic overlap is removed and a semimetal-to-semiconductor transition occurs. The transition between valence and conduction bands is a Γ–Γ direct one when strain is between +6% and +10%. Outside of this range of tensile strain, an indirect transition is predicted. The change of electronic properties with respect to strain can be explained from the geometry and charge transfer. These results establish the relationship between the properties of 1T-TiS₂ and strain, which may find utility in future electronic devices.

Computational methods

The energy and electronic properties of monolayer TiS₂ were calculated using VASP¹³ with the projector augmented wave pseudopotentials¹⁴ and GGA–PBE¹⁵ exchange–correlational functionals. The kinetic energy cutoff was set to 400 eV in the plane-wave basis set. The primary unit cell of monolayer TiS₂ was constructed with 20 Å of vacuum to eliminate possible image interactions. All layered structures were relaxed on a well-converged 25 × 25 × 1 Monkhorst–Pack¹⁶ k-point grid until the Hellmann–Feynmann forces on every ion falls under 0.001 eV Å⁻¹. Strain on the monolayer was simulated by scaling the atomic positions of the relaxed structure by the appropriate factors along the lattice vector directions a₁ and a₂. The system was then allowed to relax again within the scaled unit cell. Calculations of the electronic properties followed on a 41 × 41 × 1 k-point grid. Bader analysis was used to quantify the charge transfer between atoms.¹⁷ Calculations on bulk TiS₂ were also performed and found to be in good agreement with previous reports (see ESI† for description and band structure).

Acknowledgements

This work is supported by the Chemical Sciences, Geosciences, and Biosciences Division, Office of Basic Energy Sciences, Office of Science, U.S. Department of Energy under Award Number DE-SC0010212.

References

1. Z. Zeng, Z. Yin, X. Huang, H. Li, Q. He, G. Lu, F. Boey and H. Zhang, Angew. Chem., Int. Ed., 2011, 50, 11093–11097.
2. J. Zheng, H. Zhang, S. Dong, Y. Liu, C. T. Nai, H. S. Shin, H. Y. Jeong, B. Liu and K. P. Loh, Nat. Commun., 2014, 5, 2995.
3. M. M. Biener, J. Biener and C. M. Friend, J. Chem. Phys., 2005, 122, 034706.
4. C. Tan and H. Zhang, Chem. Soc. Rev., 2015, 44, 2713–2731.
5. C. Wan, X. Gu, F. Dang, T. Itoh, Y. Wang, H. Sasaki, M. Kondo, K. Koga, K. Yabuki, G. J. Snyder, R. Yang and K. Koumoto, Nat. Mater., 2015, 14, 622–627.
6. Z. Zeng, C. Tan, X. Huang, S. Bao and H. Zhang, Energy Environ. Sci., 2014, 7, 797–803.
7. U. Gupta, B. G. Rao, U. Maitra, B. E. Prasad and C. N. R. Rao, Chem.–Asian J., 2014, 9, 1311–1315.
8. P. Johari and V. B. Shenoy, ACS Nano, 2012, 6, 5449–5456.
9. Z. H. Ni, T. Yu, Y. H. Lu, Y. Y. Wang, Y. P. Feng and Z. X. Shen, ACS Nano, 2008, 2, 2301–2305.
10. P. Johari and V. B. Shenoy, ACS Nano, 2012, 6, 5449–5456.
11. L. Dong, A. M. Dongare, R. R. Namburu, T. P. Oapos Regan and M. Dubey, Appl. Phys. Lett., 2014, 104, 053107.
12. Y. Li, J. Kang and J. Li, RSC Adv., 2014, 4, 7396–7401.
13. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
14. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
15. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
16. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
17. W. Tang, E. Sanville and G. A. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.

---

Footnote

† Electronic supplementary information (ESI) available: The complete data set of strain-induced band gaps for mononlayer 1T-TiS₂ as well as the band structure and the density of states for bulk TiS₂ are provided. See DOI: 10.1039/c5ra16877e

---