On the mechanical stability of uranyl peroxide hydrates: implications for nuclear fuel degradation
Abstract
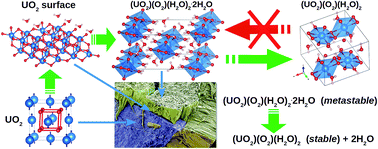
The mechanical properties and stability of studtite, (UO2)(O2)(H2O)2·2H2O, and metastudtite, (UO2)(O2)(H2O)2, two important corrosion phases observed on spent nuclear fuel exposed to water, have been investigated using density functional perturbation theory. While (UO2)(O2)(H2O)2 satisfies the necessary and sufficient Born criteria for mechanical stability, (UO2)(O2)(H2O)2·2H2O is found to be mechanically metastable, which might be the underlying cause of the irreversibility of the studtite to metastudtite transformation. According to Pugh's and Poisson's ratios and the Cauchy pressure, both phases are considered ductile and shear modulus is the parameter limiting their mechanical stability. Debye temperatures of 294 and 271 K are predicted for polycrystalline (UO2)(O2)(H2O)2·2H2O and (UO2)(O2)(H2O)2, suggesting a lower micro-hardness of metastudtite.

 Please wait while we load your content...
Please wait while we load your content...