Solvent-free 1H-tetrazole, 1,2,5,6-tetrahydronicotinonitrile and pyrazole synthesis using quinoline based ionic fluoride salts (QuFs): thermal and theoretical studies†
Abstract
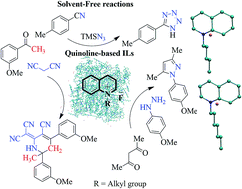
The role of ionic liquids as catalyst and solvent to mediate organic reactions is well documented. While imidazole and pyridine-based ionic liquids have traditionally been the ionic liquids of choice for organic synthesis, imidazole's inert nature and pyridine's toxicity are often viewed as impediments. In the present study, we have synthesized ionic liquids (QuFs), employing the non-toxic quinoline ring. The desired QuFs were readily prepared via N-alkylation and corresponding anion exchange with fluoride ions. The structures of the synthesized QuFs were confirmed with advanced spectroscopic techniques such as 1H and 13C NMR, IR and mass spectrometry. The potential of these newly synthesized QuFs as catalyst for click chemistry and other reactions was explored by carrying out synthesis of 5-(p-methylphenyl)-1H-tetrazole (7), 2-dicyanomethylene-6-methyl-4,6-bis(m-methoxyphenyl)-1,2,5,6-tetrahydronicotinonitrile (12), and 3,5-dimethyl-1-(p-methoxy)-1H-pyrazole (15). Detailed thermal analysis (DSC, TGA and DTG) was carried out to study the thermal stability of synthesized QuFs. Density functional theory (DFT) calculations and molecular dynamics simulations were also carried in order to establish a relationship between binding energies, and structural and dynamic characteristics of QuFs.


 Please wait while we load your content...
Please wait while we load your content...