Needle-free drop deposition: the role of elastic membranes†
Prashant R.
Waghmare
a,
Surjyasish
Mitra
b,
Naga Siva
Kumar Gunda
b and
Sushanta K.
Mitra
*b
aDepartment of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 2G8, Canada
bMicro & Nano-scale Transport Laboratory, Department of Mechanical Engineering, Lassonde School of Engineering, York University, Toronto, Ontario M3J 1P3, Canada. E-mail: sushanta.mitra@lassonde.yorku.ca; Tel: +1 416 736 5924
First published on 16th September 2015
Abstract
Contact angle measurement of low-energy surfaces (superhydrophobic, superoleophobic, etc.) with needle–drop assembly is critical for characterizing such substrates. However, it is extremely difficult to detach the needle from the drop when it is brought into contact with a characterizing substrate and often one has to report contact angles with the needle attached to the drop itself. To overcome this challenge, here we present a new technique to achieve a ‘needle-free’ drop by bringing the drop into contact with an additional elastic membrane, kept between the needle–drop assembly and the characterizing substrate. The detachment of the drop from the needle is achieved by retracting the needle–drop assembly at a finite speed and allowing the drop to receive the elastic energy of the soft flexible membrane. Such interaction of the drop with the elastic membrane allows the drop to be repelled from the elastic membrane and further be deposited on a characterizing substrate. The repelling behavior of the drop can be controlled by appropriately selecting the mechanical and wetting properties of this additional elastic membrane. This technique not only provides a needle-free drop deposition that is independent of the physical properties of the liquid and the needle but it also allows achievement of drop sizes independent of the needle diameter. Experimental analysis and theoretical investigations suggest that the mechanical properties of the elastic membrane, particularly its elasticity, play an important role towards the success of the drop deposition technique.
1 Introduction
Drop deposition on a given target substrate has a plethora of applications from characterizing the wetting properties of natural, bio-inspired, and artificial micro/nano-structured surfaces1–5 to drop impact studies to determine pre- and post-impact dynamics.6–10 In all of these examples, the critical step is to detach the drop reliably from the needle that is typically used in any drop deposition method – be it using the traditional pendant drop method6 or the drop weight method.4,11 Often this critical step poses a challenge in itself, when the surface energy of the needle–drop assembly is comparable with the surface energy of the drop and the characterizing substrate,1,12,13 or when a significant height is required to dispense the drop reliably by its own weight on a given substrate, or the needle diameter produces only a finite range of drop sizes that can be deposited onto a given substrate.14–20 In the latter case, the volume of the drop poses a limitation as one needs a significantly larger drop volume to achieve deposition due to its own weight.21Contact angle measurement has been one of the crucial tasks for accurate quantification of the wetting characteristics of a given substrate.22–26 Recently, we have proposed a ‘needle-free’ drop deposition technique for contact angle measurement of a substrate placed under-water, where a favorable spreading parameter between the drop, the surrounding liquid medium and the fluid at the interface of the surrounding medium and the needle have been appropriately configured to detach the drop from the needle.1 This study was recently extended to achieve a similar needle-free drop deposition, but in an air medium,27 which is the common scenario for characterizing substrates or performing drop-impact studies. However, this technique27 has a limitation in terms of minimum drop volume that could be detached from the needle, which has implications in terms of the drop radius in comparison to the capillary length scale for wetting studies,28 and the achievable Weber numbers and Reynolds numbers for drop impact studies17,18etc. In our previous study,27 drop detachment was achieved by bringing in an additional superhydrophobic rigid substrate through which the needle with the drop at its end was withdrawn: the interaction of the drop with the superhydrophobic substrate caused the detachment of the drop from the needle and allowed the drop to be deposited on the characterizing substrate kept below the superhydrophobic substrate. However, the extent of superhydrophobicity (attained by using a special coating to achieve a static contact angle of >165°) alone could not produce reliable drop detachment for drop volumes less than 3 μL for a needle diameter of 0.5 mm. Moreover, the argument of using a superhydrophobic coating on the needle itself to make the drop also has its own shortcomings. For that technique to work, prior knowledge of surface energies of the needle material and the characterizing substrate is required, which defeats the very purpose of developing reliable tools to measure contact angle (or to interpret the surface energies of unknown substrates).
The ‘needle-free’ drop deposition technique presented in this work is motivated by studies conducted in the literature for understanding drop impact on elastic membranes,29,30 where ethanol drops from a certain height were imparted on a stretchable polymer film below: it was found that the drop impact energy is transferred to the elastic (soft) membrane thereby reducing the drop splashing effect. Hence, it can be inferred that the additional energy transfer mechanism between the drop and a substrate can be obtained by utilizing a deformable solid substrate, as opposed to a rigid superhydrophobic surface, as done in our earlier study.27 In this present work, we take this added advantage provided by such soft membranes, and we coat such membranes with a superhydrophobic coating and utilize it as a top low-energy substrate to obtain ‘needle-free’ drop deposition in an air medium.
2 Experimental methods
A schematic of the experimental setup used in this study is shown in Fig. 1. The experimental set-up consists of a regular contact angle measurement system, DSA 100 (Krüss, Germany) with two key modifications. First, we have designed a special holder (details provided in inset diagram (a) in Fig. 1), which allows an elastic (soft) deformable membrane to be attached in a particular fashion to avoid any wrinkling in the elastic membrane and further undesirable defects due to non-uniform tension.31 To achieve this condition, the elastic membrane was secured between two rings; both rings were fabricated using the prototype machine Eden 350 V, Stratasys Ltd, USA. One end of the inner ring was clamped to the outer ring (with the membrane held in between), whereas the other end of the inner ring was fixed to the pillar-stand of the specially designed membrane holder. This holder with the elastic membrane was attached firmly to the characterizing base-table of the DSA system with nuts and bolts. This arrangement not only allowed placement of the membrane with negligible initial tension and stretching but also provided a perfectly horizontal membrane configuration, which remained parallel with the bottom characterizing substrate placed at the base of the DSA system. The second modification was to attach the needle–drop assembly to a traversing mechanism (Zaber, Canada) which allowed the needle to be retracted vertically at a speed varying between 0.1 mm s−1 and 100 mm s−1. This retraction mechanism is similar to the one used in our previous study.27 The interaction of the needle–drop assembly with the elastic membrane causes the membrane to be deflected by an amount δ in the vertical upward direction, as shown in Fig. 1(b). The elastic (soft) deformable membrane, used in this study, is plastic wrap (NoName brand) purchased from a local store (Edmonton, Canada). The wetting properties of this plastic wrap were determined by performing static equilibrium contact angle measurements (θ = 76.1° ± 6.6), using the DSA 100 (Krüss, Germany) system. This measured value is based on the Young–Laplace equation for equilibrium contact angle. A more accurate measurement can be performed by using the ‘Tadmor method’,33 however, in the case of flexible substrates, like the plastic wrap used here, the definition of a static contact angle is still in an evolving phase.34 A commercially available coating spray (NeverWet) was used to alter the wetting properties of the elastic membrane, thereby achieving an equilibrium contact angle of ∼165°. Deionized water (PURELAB Ultra, ELGA) was used as a working fluid to generate drops with the help of stainless steel needles (NE44, Krüss, Germany) and a glass syringe (SY20, Krüss, Germany). To perform needle-free drop deposition, the elastic membrane was punctured using a stainless steel needle (needle diameter 0.5 mm) approximately at the center of the membrane to create a hole. Then the needle attached to the water filled syringe was inserted through this hole. After that, a drop of a certain volume (2 μL) was generated at the tip of the needle. Finally, the drop–needle assembly was retracted with a finite velocity to allow the drop to impact on the bottom coated surface of the elastic membrane. The interaction (impact) of the drop with the elastic membrane was recorded using a Phantom V711 (ViSion Research, USA).3 Results and discussion
The ‘needle-free’ drop deposition was first attempted with an uncoated elastic membrane (a hydrophilic deformable substrate) attached to the holder, as shown in Fig. 2. A drop volume of 2 μL was produced with the needle of outside diameter 0.5 mm and was withdrawn through the elastic membrane. The needle retraction speed in this case was maintained at 30 mm s−1. Fig. 2 shows different time snaps of the interaction of the water drop with the uncoated elastic membrane. As evident from Fig. 2, the drop detaches from the needle but spreads on the elastic membrane. It is to be noted that the retraction of the needle with a finite speed along with the drop attached at its end imparts energy to the membrane during contact of the drop with the membrane causing a finite deflection in the membrane. Together with the inherent background stress, due to the special holding arrangement of the elastic membrane, the membrane vibrates post impact (see ESI Video S1†). It is evident from this video and Fig. 2(c) that in the case of an uncoated elastic membrane the drop does not detach upon impact. Rather, it spreads on the elastic membrane. This is due to the more dominant drop–membrane adhesion force by virtue of the fact that its hydrophilic nature dominates over the elastic response of the membrane, hence the cause for drop spreading. Therefore, to obtain detachment of the drop from the membrane, thereby achieving the desired ‘needle-free’ drop deposition, first the wettability of the membrane should be such that it opposes spreading and ensures minimal drop–membrane adhesion, i.e., hydrophobic/superhydrophobic. Secondly, the elasticity of the membrane should be such that the post impact elastic response dominates over drop–membrane adhesion and aids drop detachment. Hence, we present both scenarios: we changed the wettability of the membrane significantly – the hydrophilic membrane was converted into a superhydrophobic membrane using the specialized spray discussed earlier; secondly, we varied the elasticity of the membrane by using a different material for the deformable membrane, viz., polydimethylsiloxane (PDMS), details of which are discussed later.To restrict the spreading of the drop on the elastic membrane, we first applied a superhydrophobic coating to the elastic membrane and then attached the coated membrane to the holder in a similar manner as for the uncoated elastic membrane case. Here, all other experimental parameters were kept the same as shown for Fig. 2. Hence, as expected, it was found that the superhydrophobicity (low energy) of the membrane reduces the force of adhesion between the drop and the elastic membrane, thereby preventing spreading, and together with the favorable elastic response of the membrane, successful drop detachment is achieved. This ‘needle-free’ drop descends due to gravity and is subsequently deposited on the desired characterizing substrate, kept at the bottom of the elastic membrane (see ESI Video S2†). Fig. 3 shows snapshots of needle-free drop deposition using the coated superhydrophobic plastic membrane. As mentioned earlier, a second approach to detach the drop would be to change the elastic energy of the membrane. To achieve this, we replaced the elastic membrane used earlier (i.e., the plastic wrap) with a ∼1 mm thick PDMS membrane. The PDMS membrane was produced using the spin-coating technique and appropriate operating parameters32 were used to obtain the desired thickness of ∼1 mm to maintain the flexible properties of the PDMS membrane. We observed that a bare PDMS membrane is hydrophobic with an equilibrium contact angle θ = 111.8° ± 3.7. It should be noted here that contact angle measurements on soft PDMS are challenging since the applicability of Young’s law for soft solids is debatable due to the deformation of such a surface at the three phase contact line.34 Upon retracting the drop–needle assembly through it, it was found that the bare (uncoated) PDMS membrane proved to be successful in detaching the drop by the virtue of its significant elasticity, as depicted in Fig. 4. However, the energy imparted due to its elasticity and vibrating modes is high and hence we observe that the drop does not retain its original spherical shape (as opposed to the case shown for coated plastic wrap membrane in Fig. 3 where the drop retains its spherical shape), but rather breaks up into a number of satellite drops. It is to be noted that such a high magnitude of elastic energy, as observed here, is similar to the effects (i.e., flattening of the drop, recoiling, splashing and break-up35) that we witness during drop-impact on a solid substrate with a very high impact velocity. Recoil and break-up of the drop can be observed in Fig. 4(c) and (d) respectively. The wetting properties of the membrane allow the drop to spread on the membrane and we speculate that this spreading of the drop further initiates such unwanted phenomena (see ESI Video S3†). It was also observed that a certain amount of liquid volume always remains attached to the membrane. Therefore, to avoid these undesirable effects and also to achieve detachment of an intact drop from the membrane (as oppose to satellite drop formation), it is necessary to restrict spreading of the drop on the membrane. Therefore, we changed the wetting properties of the PDMS membrane in a similar way to which we earlier changed the wetting properties of the plastic wrap (the elastic membrane used in Fig. 3). We noticed that when we applied a coating to the PDMS surface, due to the superhydrophobic nature of the coated PDMS membrane (contact angle θ ≈ 165°), the entire drop was detached from the membrane and drop break-up was arrested (see ESI Video S4†). It should be noted here that, post impact, the drop, though it undergoes detachment, does not retain its original spherical shape, changing from a donut-like shape to a more elongated spherical shape at later times. Therefore, we have demonstrated that by tuning the elastic or wetting properties of the elastic membrane, one can easily obtain needle-free drop deposition In the upcoming section, we provide a theoretical analysis of this technique in terms of the wetting and elastic properties of the membrane to achieve the desired ‘needle-free’ drop deposition.
4 Theoretical analysis
To explain the four different scenarios observed, a theoretical analysis is presented. For ease of analysis, we apply conservation of energy at three different stages of the process: first, before the impact of the drop with the elastic membrane, second, at the moment of maximum deflection of the membrane due to impact and, finally, after impact when the drop detaches or spreads on the membrane. For all these stages, the system in consideration is the drop and the elastic membrane. The drop attached to the needle, before impact, corresponds to a spherical non-deformed drop of radius R, retracting with a velocity Vi. The total energy of the system at this initial stage can be expressed as, | (1) |
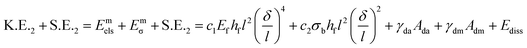 | (2) |
| E3,I = S.E.3 + Evib = [γdaπ(R02 + h02) + γdmπR02] + ρfhfl2(δ/τ)2 | (3) |
 | (4) |
| Parameters | Plastic wrap | PDMS |
|---|---|---|
| ρ | 1190 kg m−3 | 965 kg m−3 |
| E f | 2 GPa | 720 kPa |
| h f | 20 μm | 1 mm |
| δ | 2 mm | 5 mm |
| l | 2 mm | 5 mm |
| σ b | 3.12 kPa | 0.624 kPa |
| τ | 0.133 s | 0.665 s |
The situation is different for the more flexible PDMS membrane. For the uncoated hydrophobic one, even though the drop spreads initially due to inertia the elastic response of the more flexible PDMS membrane is such that vibrations of larger amplitude eventually break up the drop into satellite drops. This can be attributed to the fact that, for the more elastic PDMS membrane, less energy is available to the drop for spreading and there is more residual kinetic energy in the membrane, resulting in oscillations of larger amplitude. So, in addition to stage 3, there is another stage where the drop in its maximum spreading configuration deforms and actually breaks up and finally falls due to gravity. Also, for the superhydrophobic (coated) PDMS membrane, the drop detaches from the membrane, albeit with a deformed shape, and falls due to gravity. It should be noted that for all the scenarios discussed above, the energies E1, E2 and E3 are the same order of magnitude by virtue of the elastic collision. Unfortunately, a more detailed energy analysis is beyond the scope of the present work. On the other hand, a force analysis of the drop impact and subsequent detachment can also be performed to account for the four scenarios described above. In that regard, the competition between the force generated due to the drop impact and the drop–surface adhesion force1,36 will dictate the eventual outcome of the process. The authors would like to point out that drop impact and break up is a field in its own, while in the present work, the focus is entirely on needle-free drop deposition. Compared to our previous study,27 using a rigid hydrophobic top substrate to facilitate drop detachment, drop deposition using an elastic membrane minimizes drop deformation and energy loss upon impact and subsequent detachment due to perfectly elastic interaction, and can be considered as a lower bound of any such post impact drop deformation.
It should be noted here that the retraction velocity is important for successful drop detachment upon impact with the elastic membrane. The needle retraction velocity of 30 mm s−1 corresponds to a Weber number (We = ρVi2R/γ) much lower than unity, which is perfectly suited for successful drop detachment upon impact. For We > 1, unwanted phenomena, such as splashing upon impact or self-detachment from the needle during retraction is expected, as reported in our previous study.27 On the other hand, a very low retraction velocity will not produce a sufficient elastic response from the membrane to enable drop detachment. Instead, for such a scenario, the drop will adhere to the membrane surface.
5 Conclusions
In this work, a ‘needle-free’ drop deposition in air medium is obtained that is independent of the mechanical, geometrical and wetting properties of the needle and the characterizing substrate. This is achieved by bringing in an additional flexible substrate (a soft elastic membrane) between the needle–drop assembly and the bottom characterizing substrate. The ‘needle-free’ technique works when the needle–drop assembly is retracted upward at a finite speed, away from the characterizing substrate, and the interaction of the drop with the flexible membrane ensures negligible energy loss and drop deformation upon impact thereby allowing the drop to be detached from the needle and settle on the bottom characterizing substrate by gravity for accurate contact angle measurement of the characterizing substrate. We have considered two different kinds of membrane substrates – plastic wrap and a PDMS membrane with varying elastic properties. We also varied the wetting characteristics of each substrate by using a specialized coating to make them superhydrophobic surfaces. It was found that in the case of plastic wrap, which has an elasticity significantly smaller than the PDMS membrane, the elasticity of such a surface alone is not sufficient to detach the drop from the needle. Hence, for such low elastic energy membranes, one needs to alter the wetting characteristics of the elastic membrane so that spreading of the drop on to such surfaces can be minimized thereby achieving the desired ‘needle-free’ drop deposition in air. On the other hand, the large elasticity of the PDMS membrane creates unwanted drop splashing, break-up, etc., which to a certain extent can be arrested by again altering the wetting characteristics of the highly deformable membrane. Moreover, in our previous study,27 we observed the failure of the needle-free drop deposition for drop volumes less than 3 μL, corresponding to a needle diameter of 0.5 mm which is of same dimension as that used in our present study. This is because, in the case of a rigid solid substrate, there exists a finite gap between the needle and the inner surface of the drilled hole, which allows capillary imbibition of drops (smaller than 3 μL volume) to occur inside the gap. This problem can be avoided in case of an elastic membrane, where there exists a practically negligible gap between the needle and the flexible elastic membrane. Hence, the proposed technique eliminates the dependence of the drop diameter, to be used for characterizing a given substrate, on the needle diameter, which can be greatly advantageous to studies related to drop impact. Therefore, the ‘needle-free’ drop deposition technique, presented here, has an universal appeal and not only helps in accurately determining the contact angle of low-energy surfaces (superhydrophobic, superoleophobic, etc.) but at the same time opens up a new avenue to revisit drop impact studies with controlled drop diameters over a wide range of impact Weber numbers.Acknowledgements
Financial assistance from NSERC, through Grant No. RGPIN-2014-05236, is acknowledged here. The authors would like to thank Aleksey Baldygin, Ph.D. student in the Department of Mechanical Engineering, University of Alberta, for his help towards designing and setting up the experimental system. The authors would also like to thank Dr Siddhartha Das, who was an Assistant Professor in Department of Mechanical Engineering at the University of Alberta, and is currently at the University of Maryland, for fruitful discussions regarding drop impact study.References
- P. R. Waghmare, S. Das and S. K. Mitra, Soft Matter, 2013, 9, 7437–7447 RSC.
- D. Vadillo, A. Soucemarianadin, C. Delattre and D. Roux, Phys. Fluids, 2009, 21, 122002 CrossRef PubMed.
- X. Deng, L. Mammen, H.-J. Butt and D. Vollmer, Science, 2012, 335, 67–70 CrossRef CAS PubMed.
- O. E. Yildirim, Q. Xu and O. A. Basaran, Phys. Fluids, 2005, 17, 062107 CrossRef PubMed.
- B.-B. Lee, P. Ravindra and E.-S. Chan, Chem. Eng. Commun., 2008, 195, 889–924 CrossRef CAS PubMed.
- X. Deng, F. Schellenberger, P. Papadopoulos, D. Vollmer and H.-J. Butt, Langmuir, 2013, 29, 7847–7856 CrossRef CAS PubMed.
- P. Tsai, S. Pacheco, C. Pirat, L. Lefferts and D. Lohse, Langmuir, 2009, 25, 12293–12298 CrossRef CAS PubMed.
- D. Richard, C. Clanet and D. Quéré, Nature, 2002, 417, 811 CrossRef CAS PubMed.
- B. Qian, M. Loureiro, D. A. Gagnon, A. Tripathi and K. S. Breuer, Phys. Rev. Lett., 2009, 102, 164502 CrossRef.
- C. Antonini, A. Amirfazli and M. Marengo, Phys. Fluids, 2012, 24, 102104 CrossRef PubMed.
- B.-B. Lee, P. Ravindra and E.-S. Chan, Colloids Surf., A, 2009, 332, 112–120 CrossRef CAS PubMed.
- A. Tuteja, W. Choi, M. Ma, J. M. Mabry, S. A. Mazzella, G. C. Rutledge, G. H. McKinley and R. E. Cohen, Science, 2007, 318, 1618–1622 CrossRef CAS PubMed.
- D. Bartolo, C. Josserand and D. Bonn, J. Fluid Mech., 2005, 545, 329–338 CrossRef.
- J. C. Bird, R. Dhiman, H.-M. Kwon and K. K. Varanasi, Nature, 2013, 503, 385–388 CrossRef CAS PubMed.
- A. Yarin, Annu. Rev. Fluid Mech., 2006, 38, 159–192 CrossRef.
- D. Richard and D. Quéré, EPL, 2000, 50, 769 CrossRef CAS.
- M. Pasandideh-Fard, Y. Qiao, S. Chandra and J. Mostaghimi, Phys. Fluids, 1996, 8, 650–659 CrossRef CAS PubMed.
- D. Roux and J. Cooper-White, J. Colloid Interface Sci., 2004, 277, 424–436 CrossRef CAS PubMed.
- Y. C. Jung and B. Bhushan, Langmuir, 2008, 24, 6262–6269 CrossRef CAS PubMed.
- K. Okumura, F. Chevy, D. Richard, D. Quéré and C. Clanet, EPL, 2003, 62, 237 CrossRef CAS.
- J. Zou, P. F. Wang, T. R. Zhang, X. Fu and X. Ruan, Phys. Fluids, 2011, 23, 044101 CrossRef PubMed.
- E. Atefi, J. A. Mann Jr and H. Tavana, Langmuir, 2013, 29, 5677–5688 CrossRef CAS PubMed.
- R. Dufour, M. Harnois, V. Thomy, R. Boukherroub and V. Senez, Soft Matter, 2011, 7, 9380–9387 RSC.
- C. Fuentes, K. Beckers, H. Pfeiffer, L. Tran, C. Dupont-Gillain, I. Verpoest and A. van Vuure, Colloids Surf., A, 2014, 455, 164–173 CrossRef CAS PubMed.
- L. Gao and T. J. McCarthy, Langmuir, 2009, 25, 14105–14115 CrossRef CAS PubMed.
- L. Jenkins and A. Donald, Langmuir, 1999, 15, 7829–7835 CrossRef CAS.
- P. R. Waghmare and S. K. Mitra, J. Appl. Phys., 2014, 116, 114903 Search PubMed.
- P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer Science & Business Media, 2013 Search PubMed.
- R. E. Pepper, L. Courbin and H. A. Stone, Phys. Fluids, 2008, 20, 082103 CrossRef PubMed.
- L. Courbin, A. Marchand, A. Vaziri, A. Ajdari and H. A. Stone, Phys. Rev. Lett., 2006, 97, 244301 CrossRef.
- E. Cerda, K. Ravi-Chandar and L. Mahadevan, Nature, 2002, 419, 579–580 CrossRef CAS PubMed.
- M. Liu, J. Sun, Y. Sun, C. Bock and Q. Chen, J. Micromech. Microeng., 2009, 19, 035028 CrossRef.
- R. Tadmor, Langmuir, 2004, 20, 7659–7664 CrossRef CAS PubMed.
- A. Marchand, S. Das, J. H. Snoeijer and B. Andreotti, Phys. Rev. Lett., 2012, 109, 236101 CrossRef.
- R. Rioboo, C. Tropea and M. Marengo, Atomization Sprays, 2001, 11, 155–165 CAS.
- R. Tadmor, P. Bahadur, A. Leh, H. E. N’ guessan, R. Jaini and L. Dang, Phys. Rev. Lett., 2009, 103, 266101 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra15938e |
| This journal is © The Royal Society of Chemistry 2015 |




