Electric-field-induced rich magneto-absorption spectra of ABC-stacked trilayer graphene

Abstract

The magneto-optical spectra of ABC-stacked trilayer graphene are enriched by an electric field. A lot of prominent absorption peaks, which arise from the inter-Landau-level transitions, gradually change from twin-peak structures into double-peak ones with increasing electric-field strength. This comes from the destruction in mirror symmetry of the xy-plane and the non-equivalence of two sublattices with identical projections. Specially, a single threshold peak becomes a double-peak structure, owing to the Fermi–Dirac distribution. The absorption frequencies continuously grow or decline except for those caused by the anti-crossings of Landau levels. Also, such anti-crossings can induce extra double-peak structures.

---

Graphene, with its fascinating hexagonal lattice structure, was first fabricated by mechanical exfoliation in 2004.¹ Its unique electronic and optical properties can be easily modulated by changing the layer number,² the stacking configuration,³ the external magnetic⁴ and electric fields,⁵ and the deformed structure.⁶ These geometric varieties and tuning effects have attracted numerous theoretical and experimental studies especially for the magneto-electronic and -optical properties in few-layer graphene.^7–9 The quantized Landau levels (LLs) are strongly dependent on the stacking configuration. N-Layer graphene has N groups of conduction and valence LLs. The three highly symmetric layer configurations, AAA-, ABA-, and ABC-stacked trilayer graphene, exhibit totally different magneto-optical properties. The three categories of excitation channels, belonging to intra-group optical transitions, are revealed in AAA-stacked trilayer graphene. The inter-group LL excitations are absent because of the special relationships among the LL wave functions.¹⁰ ABA trilayer graphene is expected to present five categories of absorption peaks since its LLs can be regarded as the superposition of those of the AB-stacked bilayer and monolayer systems. Moreover, ABC-stacked trilayer graphene possesses nine categories of absorption peaks, including all the intra-group and inter-group LL excitations.¹¹ A specific magneto-optical selection rule, Δn = 1 in the variation of quantum number, is identified for the above-mentioned systems. In particular, there are three kinds of the selection rules, Δn = 0, 1, and 2, for sliding graphene with various stacking configurations.¹² On the experimental side, only the intra-group excitation channels from the first LL group in AB-stacked few-layer graphenes (N = 1–5) have been verified until now.¹³ In this work, we focus on how a uniform perpendicular electric field (E = E₀ẑ) affects the low-frequency magneto-optical properties of ABC-stacked trilayer graphene, including the structure, intensity and frequency of the absorption peaks.

We have developed a generalized tight-binding model for various external fields,^14,15 in which the Hamiltonian matrix is built from the tight-binding basis functions, i.e. the subenvelope functions on the different sublattices. The model can be further utilized to investigate the magneto-optical properties of ABC-stacked trilayer graphene in E. Detailed investigations have been performed on how the inter-LL optical transitions are diversified by the relationship between the interlayer atomic interactions and the electric field. This study shows that the electric field causes the splitting of Landau levels, and hence abundant absorption peaks are induced with E₀-dependent peak structure, frequency and intensity. A twin-peak structure or single-peak structure will be replaced by a double-peak structure at a sufficiently large electric-field strength. The extra peaks are generated by the intra-group LL anticrossings during the variation of E₀; furthermore, the abnormal E₀-dependent absorption frequencies are obtained. The theoretical predictions could be verified by the optical spectroscopy methods.^16–19

The magnetic field, electric field and interlayer atomic interactions are simultaneously taken into account in the generalized tight-binding model. The primitive unit cell of ABC trilayer graphene consists of six carbon atoms (A¹, B¹, A², B², A³, B³), where the superscripts 1, 2, and 3 correspond to the first, second, and third layer. The atomic interactions include one intralayer type (β₀ = 3.16 eV) and five interlayer types (β₀ = 3.16 eV, β₁ = 0.36 eV, β₂ = −0.01 eV, β₃ = 0.32 eV, β₄ = 0.03 eV; β₅ = 0.013 eV).²⁰ The vector potential caused by a uniform perpendicular magnetic field introduces a periodic phase in the atomic interactions. Thus, the unit cell is enlarged by 2R_B times (R_B = 79 000/B₀), and the Hamiltonian function is a 12R_B × 12R_B Hermitian matrix. Moreover, a uniform perpendicular electric field leads to a potential energy difference (V_g = E₀d; interlayer distance d = 3.35) between two neighboring layers, i.e., V_g changes the site energies of the diagonal Hamiltonian matrix elements. The eigenvalues and eigenfunctions can be solved effectively by a special diagonalization method for a band-like Hamiltonian matrix.

The optical absorption function according to the Fermi golden rule at zero temperature is directly obtained through

where the superscripts c and v represent, respectively, a conduction and a valence state, f(E^c,v(k, n)) is the Fermi–Dirac distribution function, and Γ (≃ 1 meV) is the broadening parameter. The absorption spectrum accounts for the inter-LL transitions from the occupied state to the unoccupied one. Only vertical transitions of Δk_x = 0 and Δk_y = 0 are allowed because of zero photon momentum. The absorption intensity is dominated by the velocity matrix, which is calculated by the gradient approximation.²¹ For the electric polarization Ê∥ŷ, the velocity matrix elements are obtained from the multiplication of the three matrices corresponding to the initial state, the final state and ∂H/∂k_y. The spectral intensity is dominated by the nearest-neighbor Hamiltonian matrix elements, since the in-plane atomic interaction β₀ makes the largest contribution to the inter-LL excitations. The optical transitions are available only when the subenvelope function of the Aⁱ(Bⁱ) sublattice in the initial state has the same mode as that of the Bⁱ(Aⁱ) sublattice in the final state.

In the presence of an electric field, each LL is twofold degenerate rather than the ordinary fourfold degenerate, mainly owing to the destruction of the xy-plane mirror symmetry. The six subenvelope functions are localized at the 2/6 (5/6; purple) and 4/6 (1/6; blue) positions, as shown in Fig. 1, for B₀ = 48 T and V_g = 0.23 eV. The quantum numbers of the first LL group, n^c,v_1β and n^c,v_1α, are characterized by the B¹_j and A³_j sublattices, respectively, where the subscripts β and α stand for the localized positions 2/6 and 4/6. Even with the same quantum number, the conduction and the valence LLs have their six subenvelope functions which behave differently. For example, the amplitudes of A¹_j and A²_j (B²_j and B³_j) in the n^v_1β = 4 (n^c_1β = 4) LL are much smaller than those in the n^c_1β = 4 (n^v_1β = 4) LL. In general, the subenvelope functions corresponding to the identical planar projections, (A¹_j ↔ B²_j) and (A²_j ↔ B³_j), are similar in their node numbers and amplitudes. However, the potential difference will destroy the stacking symmetry between these two sublattices, so that the subenvelope functions are no longer equivalent at a sufficiently large V_g. The sharp contrast between the amplitudes of the subenvelope functions is expected to induce dramatic changes in the absorption peaks.

Fig. 1 The first group of Landau levels and their respective six subenvelope wave functions for B₀ = 48 T and V_g = 0.23 eV.

The electric field and the atomic interactions lead to a feature-rich energy spectrum, as shown in Fig. 2(a). Some LL energies (E^c,v) monotonously increase or decrease with rising V_g, and the others demonstrate non-monotonic V_g-dependences. In particular, the intra-group LL anticrossings occur frequently during the evolution of the V_g-dependent LL energies (black circles, and green and red rectangles), since some of the LLs possess multi-modes at certain V_g ranges. The amplitudes of the main and side modes in the subenvelope functions are drastically changed.¹² For example, the subenvelope functions, (n^c_1α = 1 & n^c_1α = 4) and (n^v_1β = 1 & n^v_1β = 4), are strongly hybridized around the anticrossing point (V_g ∼ 0.19 eV), the progressions are, respectively, illustrated in Fig. 2(b) and (c) for 0.15 eV ≤ V_g ≤ 0.25 eV. After that, their quantum numbers are exchanged. The modes of the subenvelope wave functions become well-defined again with the further increase of V_g. These variations in the amplitude, waveform, and zero-point number of the subenvelope functions, which are modulated by V_g, directly reflect on the absorption spectra.

Fig. 2 (a) The two Landau-level subgroup spectra at B₀ = 48 T as a function of the electric field (V_g) illustrated in two different color codes: purple and blue. The α-type and β-type intra-group Landau-level anticrossings are indicated by red and green rectangles, respectively. (b) The variations of the A³_j subenvelope wave functions for n^c_α = 1 and n^c_α = 4 with respect to the α-type intra-group Landau-level anticrossing. (c) The variations of the B¹_j subenvelope wave functions for n^v_β = 1 and n^v_β = 4 with respect to the β-type intra-group Landau-level anticrossing.

The low-frequency absorption spectra with respect to the first group of LLs exhibit many more special peak structures as a result of being diversified by the electric field. The absorption peaks of the α- and β-type are, respectively, indicated by the blue and purple curves in Fig. 3. The threshold inter-LL excitation, coming from the optical transition: the occupied n^v₁ = 3 LL to the unoccupied n^c₁ = 2 LL, exhibits a single-peak structure for V_g = 0, which is attributed to the Fermi–Dirac distribution and the selection rule of Δn = 1.¹¹ The LLs with the different localization positions make the same contribution. The LL degeneracy is destroyed by V_g; therefore, the threshold excitation becomes a double-peak structure. The lower- and higher-frequency comes from n^v_1β = 2 → n^c_1β = 3 and n^v_1α = 3 → n^c_1α = 2 (arrows in Fig. 2(a)) with their subenvelope functions localized at the 2/6 and 4/6 positions, respectively. The peak structures stays unchanged, and the frequencies increase with the increment of V_g. However, the other absorption peaks for V_g = 0 possess twin-peak structures with a similar absorption intensity,¹¹ which is caused by the asymmetric energy spectrum between the occupied and unoccupied LLs. Such structures also emerge in two different localization positions, 2/6 and 4/6 for a small V_g. As denoted by and in Fig. 3, where two twin-peak structures or four absorption peaks are displayed at V_g = 0.01 eV. With the further increase of V_g, they are replaced by a double-peak structure (black circle at V_g = 0.11 eV) since a certain peak of the twin-peak structure has almost vanished. In other words, the two peaks in a double-peak structure, respectively, arise from the inter-LL transitions with the distinct localization centers of 2/6 and 4/6. Apparently, the dramatic changes in the peak structure indicate strong competition between the interlayer atomic interactions and the electric field.

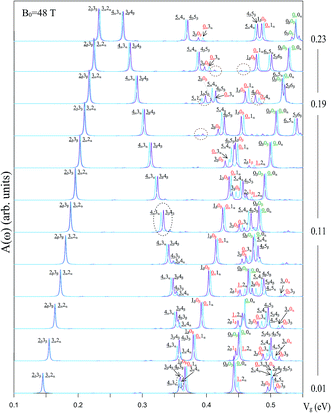Fig. 3 The α- and β-type optical spectra in the low-frequency region from V_g = 0.01 to 0.23 eV are shown by the blue and purple colors, respectively.

The V_g-induced rich absorption spectra deserve a closer investigation. The equivalent sublattices, (A¹_j ↔ B²_j) and (A²_j ↔ B³_j), with identical planar projections, possess similar waveforms and amplitudes for the subenvelope functions.¹¹ The equivalence is destroyed when an electronic static gate voltage induces a potential energy difference on the distinct layers. At a sufficiently large V_g, the amplitudes of A¹ and A² in the valence LLs and those of B² and B³ in the conduction LLs become very small (red rectangles in Fig. 1). And the spectral intensity of the absorption peak is proportional to the inner product calculated from the Bⁱ sublattices of n^v_β = 3 (n^v_α = 4) and the Aⁱ sublattices of n^c_β = 4 (n^c_α = 3). However, for the absorption peak the intensity is determined by the inner product of the Aⁱ sublattices in n^v_β = 4 (n^v_α = 3) and the Bⁱ sublattices in n^c_β = 3 (n^c_α = 4). As a result, the latter is much weaker than the former.

The electric field induces the intra-group LL anticrossings and thus the extra double-peak structures. The existence of extra absorption peaks is mainly controlled by the weight of the side mode in the progressive LL. For example, the spectral intensities of 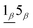and (brown circles in Fig. 3) begin to gradually rise from V_g = 0.15 eV and reach their maximums when V_g gets to 0.19 eV, since the subenvelope functions of n^v(c)_1β(α) = 1 and n^v(c)_1β(α) = 4 are strongly hybridized with each other (Fig. 2(b) and (c)). After that, the intensities drop down low under the increasing V_g and disappear when the quantum numbers of the subenvelope functions are restored, becoming well-defined again.

The low-lying inter-LL absorption frequencies (ω_n̲n) strongly depend on the electric-field strength. The absorption frequencies of the double-peak structures monotonously decrease as V_g increases, while the opposite is true for the threshold double-peak ones, as shown in Fig. 4. Such dependences are revealed to originate from the V_g-dependent LL energies. The perpendicular external electric field induces the opening of the energy gap; therefore, the absolute energies of the six valence and conduction LLs respectively located at the 2/6 and 4/6 positions, which are near the Fermi level and designated to the quantum numbers 0, 1 and 2, will rise with the increasing V_g. However, the behavior of the other LLs at the 2/6 (4/6) position is opposite to these six LLs. As a result, the energy differences of the LLs can be clearly reflected by ω_n̲n. Moreover, ω_n̲n exhibits some discontinuous V_g-dependent structures at certain electric field strengths (Fig. 4, black circles), mainly owing to the intra-group LL anticrossings. The aforementioned characteristics of the V_g-induced magneto-absorption spectra, like the peak structure, peak intensity, and V_g-dependent absorption frequency, could be verified by optical spectroscopy methods, such as transmission,^22,23 reflection^24,25 and Raman scattering spectroscopies.^16,26,27

Fig. 4 The V_g-dependent frequencies of the low-lying inter-Landau level absorption peaks.

The generalized tight-binding model was developed to investigate the optical properties of ABC-stacked trilayer graphene in magnetic and electric fields. The prominent LL magneto-absorption peaks are diversified by the electric field. With increased V_g, the twin-peak structures gradually change into the double-peak ones. The former and the latter, which correspond to the inter-LL transitions with the same and different localization centers, are respectively caused by the asymmetric LL energy spectrum and the destruction of both the mirror symmetry and the equivalence of two sublattices. The special peak structures are mainly determined by the competition between the interlayer atomic interactions and the electric-field strength. Especially, a threshold single peak is replaced by a double-peak structure because of the Fermi–Dirac distribution. Moreover, the anti-crossings of the LLs can create extra double-peak structures and thus disrupt the dependence of the peak frequency on V_g. The experimental examinations of the V_g-induced magneto-optical spectra are useful in identifying the stacking configurations among few-layered graphene systems.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. J. Nilsson, A. C. Neto, F. Guinea and N. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045405.
3. M. Koshino, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125304.
4. M. O. Goerbig, Rev. Mod. Phys., 2011, 83, 1193.
5. E. V. Castro, K. Novoselov, S. Morozov, N. Peres, J. L. Dos Santos, J. Nilsson, F. Guinea, A. Geim and A. C. Neto, Phys. Rev. Lett., 2007, 99, 216802.
6. J. H. Wong, B. R. Wu and M. F. Lin, J. Phys. Chem. C, 2012, 116, 8271.
7. E. McCann and V. I. FalâĂŹko, Phys. Rev. Lett., 2006, 96, 086805.
8. T. Morimoto, M. Koshino and H. Aoki, J. Phys.: Conf. Ser., 2013, 012028.
9. P. Moon and M. Koshino, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195458.
10. C. W. Chiu, S. C. Chen, Y. C. Huang, F. L. Shyu and M. F. Lin, Appl. Phys. Lett., 2013, 103, 041907.
11. Y. P. Lin, C. Y. Lin, Y. H. Ho, T. N. Do and M. F. Lin, Phys. Chem. Chem. Phys., 2015, 17, 15921.
12. Y. K. Huang, S. C. Chen, Y. H. Ho, C. Y. Lin and M. F. Lin, Sci. Rep., 2014, 4, 7509.
13. S. Berciaud, M. Potemski and C. Faugeras, Nano Lett., 2014, 14, 4548.
14. J. H. Ho, Y. H. Lai, Y. H. Chiu and M. F. Lin, Phys. E, 2008, 40, 1722.
15. S. C. Chen, T. S. Wang, C. H. Lee and M. F. Lin, Phys. Lett. A, 2008, 372, 5999.
16. A. C. Ferrari and D. M. Basko, Nat. Nanotechnol., 2013, 8, 235.
17. K. F. Mak, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 104, 176404.
18. K. F. Mak, L. Ju, F. Wang and T. F. Heinz, Solid State Commun., 2012, 152, 1341.
19. C. Cong, J. Jung, B. Cao, C. Qiu, X. Shen, A. Ferreira, S. Adam and T. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235403.
20. J. C. Charlier, J. P. Michenaud and P. h. Lambin, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4540.
21. M. F. Lin and K. W. K. Shung, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17744.
22. C. Li, M. T. Cole, W. Lei, K. Qu, K. Ying, Y. Zhang, A. R. Robertson, J. H. Warner, S. Ding and X. Zhang, et al., Adv. Funct. Mater., 2014, 24, 1218–1227.
23. P. Plochocka, C. Faugeras, M. Orlita, M. Sadowski, G. Martinez, M. Potemski, M. Goerbig, J.-N. Fuchs, C. Berger and W. De Heer, Phys. Rev. Lett., 2008, 100, 087401.
24. Z. Yan, Y. Liu, L. Ju, Z. Peng, J. Lin, G. Wang, H. Zhou, C. Xiang, E. Samuel and C. Kittrell, et al., Angew. Chem., 2014, 126, 1591.
25. B. Daas, K. Daniels, T. Sudarshan and M. Chandrashekhar, J. Appl. Phys., 2011, 110, 113114.
26. C. Cong, T. Yu, K. Sato, J. Shang, R. Saito, G. F. Dresselhaus and M. S. Dresselhaus, ACS Nano, 2011, 5, 8760–8768.
27. K. Kim, S. Coh, L. Z. Tan, W. Regan, J. M. Yuk, E. Chatterjee, M. Crommie, M. L. Cohen, S. G. Louie and A. Zettl, Phys. Rev. Lett., 2012, 108, 246103.

---