Influence of the double bond on the hydrogen abstraction reactions of methyl esters with hydrogen radical: an ab initio and chemical kinetic study†
Abstract
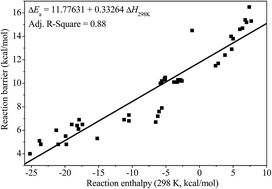
This work reports a systematic ab initio and chemical kinetic study of the rate constants for hydrogen atom abstraction reactions by hydrogen radical on the isomers of unsaturated C6 methyl esters. Geometry optimizations and a frequency calculations of all of the species involved, as well as the hindrance potential descriptions for reactants and transition states have been performed at the B3LYP/6-311G(2d,d,p) level of theory implemented in the composite CBS-QB3 method. The intrinsic reaction coordinate (IRC) calculations are performed to verify that the transition states are the right minima connecting the reactants and the products. The hindered rotor approximation has been used for the low frequency torsional modes in both reactants and transition states. The high-pressure limit rate constants for every reaction channel in certain methyl ester fuel molecules are calculated via conventional transition-state theory with the asymmetric Eckart method for quantum tunneling effect by using the accurate potential energy information obtained with the CBS-QB3 method. The individual rate constants at different reaction sites for all the methyl esters in the temperature range from 500 to 2500 K are calculated and fitted to the modified three parameters Arrhenius expression using least-squares regression. Further, a branching ratio analysis for each reaction site has also been investigated for all of the methyl esters. To the best our knowledge, it is the first systematic theoretical studies to investigate the influence of the double bond on the elementary reaction kinetics of methyl esters. This work not only provides accurate reaction rate coefficients for combustion chemical kinetic modeling, but also helps to gain further insight into the combustion chemistry of biodiesel in future investigations.

 Please wait while we load your content...
Please wait while we load your content...