Synthesis and magnetic properties of nano-dimensional Fe_1−xCu_xAl₂O₄ (0.3 ≤ x ≤ 0.8)

Abstract

Here we report, the sol–gel synthesized, microstructural analysis, surface and magnetic properties of solid solutions of Fe_1−xCu_xAl₂O₄. The singular phase of the samples for x values varied between 0.3 and 0.8 at 700 °C has been obtained. The powder X-ray diffraction, electron diffraction and HRTEM analysis reveal that the particle size systemically increases with the increase in x value. The XPS studies have confirmed the presence of Cu²⁺ species with a (Fe + Cu)/Al surface atomic ratio close to the bulk stoichiometric value. Unlike the common magnetic spinels with B-site magnetic cations, Fe_1−xCu_xAl₂O₄ shows only A-site magnetism in a diamond-type lattice. The samples with smaller particle size, namely the samples for x = 0.3 and 0.4 exhibit small magnetization. The origin of such magnetism is attributed to the inversion in the spinel structure and the defect induced magnetism. Except for the x = 0.7 sample, all other samples show spin glass behavior.

---

Introduction

Transition metal oxides are always an attractive field to the materials community for their wide range of fascinating physical properties and numerous technological applications. The oxide spinels have been investigated extensively for their exotic magnetic properties as well as from the view point of practical usefulness as magnetic materials, semiconductors, pigments, catalysts, refractory materials or as model systems to explore the relative stabilities of cations in octahedral and tetrahedral coordination.^1–5 A majority of the ternary oxides of the general formula AB₂O₄ adopt the spinel structure accommodating a wide range of cation distribution that consequently leads to an interesting range of chemical and physical properties. Generally the spinel structure can be described as a face centered cubic packing arrangement of oxygen anions, where 1/8 tetrahedral and 1/2 octahedral holes are occupied respectively, by the divalent A-cation and trivalent B-cations which crystallizes in cubic structure with the space group Fd3̄m. The site exchange between A and B resulting the mixed A and B cations in the octahedral and B in the tetrahedral sites leads to the inverse spinel structure. Even several binary oxides like Fe₃O₄ or Co₃O₄ can also adopt spinel structure due to the stability in variable oxidation states of transition metal ions. Fe₃O₄ (loadstone) is a well documented inverse spinel with omnipresent magnetic properties and is recently revived due to the interest in biomedical applications.^6,7 Co₃O₄ has recently received interest for the catalytic activity and gas sensing properties.^8,9

Most of the investigations are carried out on those spinels where magnetic ions occupy the octahedral B-site thereby forming a frustrated pyrochlore type spin lattice. However, much less is known about the spinels where magnetic ions are occupied in tetrahedral A-site and B-site is non-magnetic. The A-site forms diamond lattice which also suffers from frustration. The spinel aluminates of the general formula MAl₂O₄ (M = Fe, Co, Ni, Cu and Zn) in its nano crystalline form have revived huge research interest because of their versatile applications. The aluminates have high specific strength and stiffness, thermal stability, hydrophobicity, low surface acidity, low cost of production and have a wide range of applications.^10–12 In spite of large magnetic dilution by aluminium the magnetic properties of FeAl₂O₄ (hercynite) is interesting and gaining importance due to its potential application as a magnetic material.^13–16 FeAl₂O₄ exhibits normal spinel structure though the inversion may take place depending on the synthesis condition.¹⁷ There are very few reports on the synthesis and magnetic properties of FeAl₂O₄ probably due to the difficulty to stabilize the phase at a lower temperature. Tristan et al. have reported the absence of any long range magnetic ordering in hercynite though it exhibits a maximum around 12 K in susceptibility curve.¹⁶ Fukushima et al. have shown that the microwave synthesized FeAl₂O₄ form magnetic clusters with large magnetization which are formed at the grain boundary of the smaller crystallites by partial replacement of Al³⁺ by Fe²⁺.¹⁵ Dutta et al. have reported the spin glass behavior of almost chemically ordered FeAl₂O₄.¹³ In this sense, we consider it is worth investigating the magnetic behavior of FeAl₂O₄ in its nanodimension though its synthesis is challenging.

We have applied the sol–gel/solution combustion method to synthesize FeAl₂O₄ and found the difficulty to stabilize the pure FeAl₂O₄ phase at lower temperature. This drives us to replace part of the iron by copper keeping in mind the aspiration of catalytic use of Fe_1−xCu_xAl₂O₄ solid solution for oxidation catalysis.¹⁸ It has been reported that the cubic normal spinel CuAl₂O₄ can be synthesized at 800 °C and at lower temperature the predominant formation of CuO takes place.^19,20 Thus, low temperature synthesis of CuAl₂O₄ is again a challenging issue. From the magnetic point of view CuAl₂O₄ exhibits spin glass behavior.²¹ Though we could not get pure CuAl₂O₄ in our synthetic strategy like FeAl₂O₄, we have been able to synthesize the solid solutions of Fe_1−xCu_xAl₂O₄ at 700 °C in nanodimensional scale in a limited range of x = 0.3 to 0.8 by sol–gel method. We have observed some interesting magnetic features in Fe_1−xCu_xAl₂O₄ (x = 0.3, 0.4, 0.5 and 0.7) samples. The magnetic property of x = 0.8 is not so interesting and thus it is not discussed here. We restrict our discussion to Fe_1−xCu_xAl₂O₄ for x = 0.3–0.7. Special emphasis is given for the lower copper loaded samples, i.e. x = 0.3 and 0.4 for their smaller particle size (<10 nm) and associated captivating magnetic behavior.

Experimental

Preparation of materials

The Fe_1−xCu_xAl₂O₄ (0.3 ≤ x ≤ 0.8) samples were synthesized by sol–gel/solution combustion method using nitrate salts of copper, iron and aluminum and anhydrous citric acid [C₆H₈O₇] as the combustion agent. All the reagents were purchased from Merck India (99%). Specifically, the preparation of Fe_0.6Cu_0.4Al₂O₄ involved the combustion of Al(NO₃)₃·9H₂O, Fe(NO₃)₃·9H₂O and Cu(NO₃)₂·3H₂O with citric acid according to the molar ratio of 2 : 0.6 : 0.4 : 12. In a typical synthesis, 6 g of Al(NO₃)₃·9H₂O, 1.9385 g of Fe(NO₃)₃·9H₂O, 0.7729 g of Cu(NO₃)₂·3H₂O were dissolved in 80 mL of Millipore water to make a homogeneous solution in a beaker with magnetic stirrer. About 20 mL of diluted nitric acid (1 mL 70% nitric acid diluted to 100 mL Millipore water) was then added to the mixture to prevent the hydrolysis of the salts. Then 18.44 g of citric acid (CA) was added to the resulting solution in order to reach the desired molar ratio (total metal : CA) of 1 : 4. The solution thus obtained was kept overnight at 70 °C under stirring condition. This was followed by an increase of temperature to 250 °C when evaporation took place eventually leading to the formation of citrate gel. At the point of complete evaporation, the xerogel started to burn with the release of brown colored fumes in a self propagating manner to produce a black colored fluffy precursor. The precursor (the black powder formed by burning out the gel) was ground using a mortar, placed in an alumina crucible and calcined at 700 °C for 20 h in air at the heating rate of 10 °C min⁻¹ to get the required spinel oxide material.

Physical characterization

The powder X-ray diffraction (PXRD) data were registered with a Bruker D8 Advance X-ray diffractometer using Cu Kα radiation (λ = 1.5418 Å) operating at 40 kV and 40 mA. The XRD patterns were recorded in the 2θ range of 10–100° using Lynxeye detector (1D mode) with a step size of 0.02° and a dwell time of 1 s per step and analyzed by ICDD (International Centre for Diffraction Data) database for phase identification.

The transmission electron microscope (TEM), electron diffraction (ED) and high resolution TEM (HRTEM) experiments were performed on a FEI Tecnai G2 30 UT LaB₆ microscope operated at 300 kV and having 0.17 nm point resolution. The high-angle annular dark field scanning transmission electron microscopy (HAADF-STEM) and the energy-dispersive X-ray spectroscopy (EDX) elemental mapping analysis were performed on a JEM ARM200F cold FEG double aberration corrected electron microscope operated at 200 kV and equipped with a large solid-angle CENTURIO EDX detector and Quantum EELS spectrometer. Samples for TEM were ground powder under methanol, and the resulting dispersion was transferred to a holey carbon film deposited on Ni supported grid.

Surface characterization was done with X-ray photoelectron spectroscopy (XPS) in a SPECS spectrometer using non-monochromatic AlKα radiation (1486.6 eV) as an X-ray source run at 150 W (12 kV, 12.5 mA). The binding energies reported here were referenced with C1s peak at 284.6 eV. For XPS analysis, powder samples were mounted on the sample holder after making into small pellets and kept in the preparation chamber at ultrahigh vacuum (UHV) at 10⁻⁸ Torr for 5 h in order to desorb any volatile species present on the surface. After 5 h, samples were placed into analyzer chamber with UHV at 10⁻¹⁰ Torr. All individual spectra were recorded with pass energy and step increment of 40 and 0.05 eV, respectively. Relative surface concentrations (at%) of constituent elements were estimated using respective peak area after Shirley background subtraction, atomic sensitivity factors and instrument transmission factor.

The dc magnetization measurements were performed using a superconducting quantum interference device (SQUID) magnetometer with a variable temperature cryostat (Quantum Design, San Diego, USA). The ac susceptibility, χ_ac(T) was measured with a PPMS (Quantum Design, San Diego, USA) with the frequency ranging from 10 Hz to 10 kHz. All the magnetic measurements were performed on powder samples putting inside a Teflon capsule.

Results and discussion

Structural characterization

The PXRD patterns of the Fe_1−xCu_xAl₂O₄ (x = 0.3, 0.4, 0.5 and 0.7) spinels are shown in Fig. 1. All the diffraction peaks can be indexed according to the cubic (Fd3̄m) structure in agreement with the literature report for the CuAl₂O₄ spinel (JCPDS 01-1153). The absence of any additional peak in the PXRD pattern demonstrates that there are no secondary phases such as CuO, Al₂O₃ or Fe₂O₃ in the samples. On either side of the copper doping limit (0.3 ≤ x ≤ 0.8) we are not able to get a singular phase following the present synthetic strategy. The cell parameters are obtained from Rietveld analysis of the lattice structure performed using the FULLPROF refinement program.²² These values are listed in Table 1. It is expected that the substitution of larger Fe²⁺ by smaller Cu²⁺ should contract the lattice. However, we noticed slight increase in lattice constant. Such unusual lattice expansion is not clear to us at this moment but it could be related to the Jahn–Teller effect of Cu²⁺ in the B-site arising out of inversion effect. Such an expansion due to the Jahn–Teller effect of Cu²⁺ has been observed in Ni–Cu–Zn ferrite spinel.²³

Fig. 1 The X-ray diffraction patterns of (a) Fe_0.7Cu_0.3Al₂O₄, (b) Fe_0.6Cu_0.4Al₂O₄, (c) Fe_0.5Cu_0.5Al₂O₄ and (d) Fe_0.3Cu_0.7Al₂O₄.

Table 1 The Rietveld refined lattice parameters (space group: Fd3̄m) for Fe_1−xCu_xAl₂O₄ spinels and the particle size determined from PXRD patterns using Scherrer's formula

Spinel composition	Cell constant (Å)	Cell volume (Å^3)	χ^2	RBragg (%)	Rf (%)	Particle size (nm)
Fe0.7Cu0.3Al2O4	8.089(2)	529.278	4.73	23.4	5.95	6
Fe0.6Cu0.4Al2O4	8.091(4)	529.739	3.24	13.1	5.05	8
Fe0.5Cu0.5Al2O4	8.094(6)	530.299	3.52	9.54	3.65	13
Fe0.3Cu0.7Al2O4	8.097(2)	530.933	2.98	8.07	2.84	19

---

The average particle size was calculated from the diffraction patterns using Scherrer's formula given by:²⁴ D_hkl = Kλ/β cos θ where D_hkl, λ, β and θ are crystallite size, wavelength of X-ray, full width at half maximum (FWHM) of diffraction peaks of the hkl plane and the diffraction angle, respectively. The values of β are extracted from the fitting of the peak to Gaussian distribution for all the major peaks. Putting the values of λ = 1.5418 Å and K = 0.91, the obtained average grain size for all the samples are presented in Table 1. The smaller size particles of the order of less than 10 nm are obtained for x = 0.3 (6 nm) and 0.4 (8 nm) samples. On the other hand, for the higher copper loaded samples the particle size becomes larger, namely 13 nm and 19 nm for x = 0.5 and x = 0.7, respectively synthesized in an identical condition. This observation is very consistent with the microscopic analysis discussed below.

Microstructural analysis

In Fig. 2, the typical TEM images for all the four samples with the corresponding ring ED patterns in the inset are shown. All ED patterns can be completely indexed based on spinel cubic structure (Fd3̄m, JCPDS 01-1153). The absence of any additional peak in the PXRD pattern demonstrates that there are no spurious phases. The particles sizes for Fe_0.3Cu_0.7Al₂O₄, Fe_0.5Cu_0.5Al₂O₄, Fe_0.6Cu_0.4Al₂O₄, and Fe_0.7Cu_0.3Al₂O₄ samples are found to be in the range of 5–60 nm. One can clearly visualize that the diffraction rings for Fe_0.7Cu_0.3Al₂O₄ sample (Fig. 2(a)) is of more dense character compared to that of the Fe_0.6Cu_0.4Al₂O₄ sample (Fig. 2(b)), whereas the other two samples Fe_0.5Cu_0.5Al₂O₄ and Fe_0.3Cu_0.7Al₂O₄ exhibit more separate diffraction spots (Fig. 2(c) and (d)). These results are of clear indication of the large particle sizes for Fe_0.5Cu_0.5Al₂O₄ and Fe_0.3Cu_0.7Al₂O₄ samples compared to the other lower copper loaded samples. These are in corroboration with the particle sizes obtained from Scherrer's formula. This was further confirmed by HRTEM measurements for Fe_0.6Cu_0.4Al₂O₄ and Fe_0.3Cu_0.7Al₂O₄ samples. The HRTEM evidence of the structure and morphology of the individual particles is presented in Fig. 3 and 4 for Fe_0.6Cu_0.4Al₂O₄ and Fe_0.3Cu_0.7Al₂O₄ samples, respectively. It is apparent that the particles are highly crystalline in all size range. The bigger size particles in Fe_0.3Cu_0.7Al₂O₄ sample demonstrates the twin structure with a (111) twinning plane (Fig. 4(a)). The EDX mapping of Fe_0.6Cu_0.4Al₂O₄ materials shows that all elements (Cu, Al, Fe and O) are distributed homogeneously throughout the nanoparticles (Fig. 5). No segregation of any other elements or secondary phases has been observed by HRTEM.

Fig. 2 Low magnification TEM images and the corresponding ring ED patterns of (a) Fe_0.7Cu_0.3Al₂O₄, (b) Fe_0.6Cu_0.4Al₂O₄, (c) Fe_0.5Cu_0.5Al₂O₄ and (d) Fe_0.3Cu_0.7Al₂O₄.

Fig. 3 The HRTEM images of selected nanoparticles of Fe_0.6Cu_0.4Al₂O₄ sample with different size and the corresponding FT patterns: (a) – tens of nanometers in [011] zone axis orientation and (b) – around 10 nm in [112] zone axis orientation.

Fig. 4 The HRTEM images of selected nanoparticles of Fe_0.3Cu_0.7Al₂O₄ sample with different size and the corresponding FT patterns: (a) – tens of nanometers in [011] zone axis orientation and (b) – around 15 nm in [−122] zone axis orientation. See the presence of multi twinning with (111) twin plane for the big size nanoparticles.

Fig. 5 Atomic EDX maps of Fe_0.6Cu_0.4Al₂O₄ sample showing homogeneous distribution of Fe, Cu, Al and O elements within the nanoparticles.

XPS studies

Extensive XPS studies of Fe_1−xCu_xAl₂O₄ spinels were carried out to investigate the elemental oxidation states and their relative surface concentrations. The Cu2p core level, CuLMM and Fe2p core level spectra in various Cu substituted FeAl₂O₄ are shown in Fig. 6. The Cu2p_3/2,1/2 peaks displayed in top left panel of the figure are resolved into spin–orbit doublets. Accordingly, Cu2p_3/2,1/2 core level peaks around 933.5 and 953.4 eV with corresponding satellite peaks and spin–orbit separation of 19.9 eV are assigned to Cu²⁺ in these type of materials.^18,25,26 Satellite peaks are characteristics of oxidized transition metals especially, Fe, Co, Ni and Cu.²⁷ It has been well documented that an additional excitation of a second electron occurs during emission of a photoelectron of a core level creating a hole in it. Sudden creation of a hole in Cu2p⁶ filled orbital from Cu²⁺ ion present in the material makes Cu³⁺ ion and it becomes unstable. Therefore, an electron transfer from O2p level to Cu3d level occurs that leads to satellite peaks in the Cu2p core level spectra as seen in the figure. It is to be noted that satellite peak (S) to main Cu2p_3/2 core level peak (M) intensity ratio (I_S/I_M) in CuO is found to be 0.55.^28–30 In the present study, intensity ratios obtained from the areas under the satellite and main peaks after background subtraction are calculated to be in the range of 0.2 to 0.3 that is lower than the value of CuO. It indicates that Cu²⁺ species present in these materials are in slightly reduced state.

Fig. 6 Cu2p core level (top left), CuLMM (top right) and Fe2p core level (bottom) of (a) Fe_0.7Cu_0.3Al₂O₄, (b) Fe_0.6Cu_0.4Al₂O₄, (c) Fe_0.5Cu_0.5Al₂O₄ and (d) Fe_0.3Cu_0.7Al₂O₄ spinels.

The X-ray initiated Auger electron spectra (XAES) of Cu of these spinels were also recorded to ascertain the oxidation state of Cu and are presented in top right panel of the figure. The characteristic intense peak around 917.1 eV in CuLMM spectra is associated with Cu²⁺ species present in these spinels.^31,32 Thus, XAES results of these Cu substituted spinels agree well with their XPS results.

Further, Fe2p core level spectra of Fe_1−xCu_xAl₂O₄ spinels displayed in bottom panel of the figure contain 2p_3/2 and 2p_1/2 peaks at 710.9 and 724.4 eV corresponding to Fe²⁺ in FeAl₂O₄.³³ However, from the above analysis of Cu oxidation state, the possibility of the presence of Fe³⁺ in this kind of system cannot be completely ruled out. Al is observed to be present in +3 oxidation state in all the materials. The O1s core level spectra show the main peak around 530.5 eV that is attributed to this type of oxide.³¹ Relative surface concentrations of Fe, Cu, Al and O are calculated from the integrated peak areas of Fe2p, Cu2p, Al2p and O1s core level spectra that are given in Table 2. The ratios of combined surface concentrations of Fe and Cu to Al are observed to be in the range of 0.46 to 0.53. This indicates that Fe to Al ratio of 1 : 2 is maintained closely after doping of Cu in the A (Fe) position of the AB₂O₄ spinel oxide.

Table 2 Relative surface concentrations (at%) of Fe, Cu, Al and O in Fe_1−xCu_xAl₂O₄ evaluated from XPS studies

Spinel materials	Fe	Cu	Al	O	(Fe + Cu)/Al
Fe0.7Cu0.3Al2O4	8.85	3.65	26.04	61.46	0.48
Fe0.6Cu0.4Al2O4	7.76	4.43	26.30	61.51	0.46
Fe0.5Cu0.5Al2O4	6.96	5.21	25.63	62.20	0.47
Fe0.3Cu0.7Al2O4	6.60	7.36	26.50	59.54	0.53

---

Magnetic properties

Fig. 7 shows the temperature dependent magnetization for all the samples measured under an applied field of 100 Oe. The zero field cooled (ZFC) and field cooled (FC) data for Fe_0.7Cu_0.3Al₂O₄ and Fe_0.6Cu_0.4Al₂O₄ samples show strong divergence at low temperature region. However, in the case of Fe_0.7Cu_0.3Al₂O₄ sample the divergence extends up to room temperature. The ZFC data exhibit a round shape maximum at ∼230 K and a sharp drop in the magnetization at ∼35 K, whereas the FC data increase gradually with the decrease of temperature and a kink corresponding to the ZFC magnetization drop (Fig. 7(a)). A similar feature is noticed for Fe_0.6Cu_0.4Al₂O₄ sample. However, in this case, the ZFC data exhibit two peaks—one centered around 200 K and the second one around 35 K (Fig. 7(b)). The FC data follow ZFC till ∼100 K followed by a rapid increase in the magnetization with the decrease in temperature (Fig. 7(b)). Thus, the thermomagnetic irreversibility temperature where ZFC–FC diverge, (T_irr) for x = 0.4 sample is much lower than that for the x = 0.3 sample. However, for the higher copper doped samples (x = 0.5 and 0.7) such divergence largely shifts to lower temperatures (Fig. 7(c) and (d)). Though the ZFC data exhibits a peak around 15 K and 10 K for x = 0.5 and x = 0.7 samples, respectively, the FC data show monotonous increase with decreasing temperature (Fig. 7(c) and (d)). The strong thermomagnetic irreversibility may be originated from the glassy magnetic behavior or from the electronic phase separation of the systems. The genesis of such distinct features of these solid solutions may be associated with the change in interaction strength of iron and copper with the variation in compositions.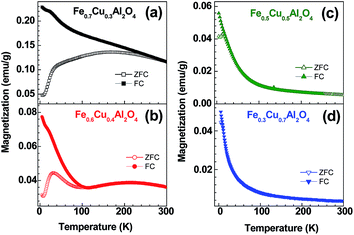

Fig. 7 Temperature dependent magnetization of (a) Fe_0.7Cu_0.3Al₂O₄, (b) Fe_0.6Cu_0.4Al₂O₄, (c) Fe_0.5Cu_0.5Al₂O₄ and (d) Fe_0.3Cu_0.7Al₂O₄ measured under an applied field of 100 Oe.

From the above results it is clear that the magnetic state of the lower copper doped samples is indeed complex in comparison with the higher doped samples. More importantly, unlike the x = 0.3 sample, the x = 0.4 sample exhibits a prominent peak in ZFC around 35 K. We believe that a detailed insight on the x = 0.4 sample will rationalize the x = 0.3 sample as well. Therefore, we have extended our investigations on x = 0.4 sample. Fig. 8 shows the ZFC & FC curves of Fe_0.6Cu_0.4Al₂O₄ in the applied fields of 50 Oe, 100 Oe and 1000 Oe. There is a strong divergence between ZFC and FC data that decreases with the increase in applied field. The existence of two peaks is clearly visualized for ZFC data at 50 and 100 Oe (Fig. 8(a) and (b)). The lower temperature peak is not observed in FC data except a small kink at ∼30 K (close to ZFC peak) (Fig. 8(a) and (b)). The broad maxima at higher temperature (∼230 K) become suppressed in 1000 Oe for both the ZFC and FC data (Fig. 8(c)). We have noticed that the divergence between ZFC and FC magnetization shifts to lower temperatures with the increase of applied field. The observation of magnetic irreversibility below 75 K for 1000 Oe field suggests that the system is not magnetically saturated even at 1000 Oe. In all the cases, the FC data at lower temperatures increases below 100 K. The ZFC data depicts a cusp like feature around 35 K, which shifts toward low temperature with increasing fields and this suggests a spin glass-type origin. There is no signature of magnetic saturation down to 2 K and an upturn in the ZFC is observed below 10 K, indicating the absence of any long range ferromagnetic ordering at low temperature.

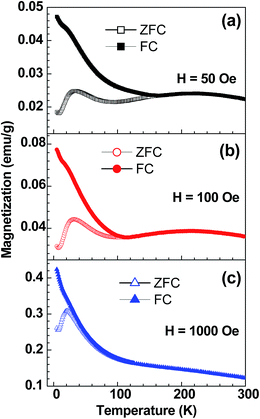Fig. 8 Temperature dependent magnetic susceptibility of Fe_0.6Cu_0.4Al₂O₄ at different applied fields: (a) 50 Oe, (b) 100 Oe and (c) 1000 Oe.

To get a better understanding of the magnetic ground state at lower temperatures we have carried out isothermal magnetization measurements at several temperatures for all the samples and these are shown in Fig. 9. For x = 0.3, 0.4 and 0.5 samples, the M(H) curves registered at 5 K exhibit small hysteresis loop and the shape of the curve is typical for a spin glass type system. The coercive field (H_C) decreases with the increase in x values (980 Oe for x = 0.3; 930 Oe for x = 0.4; 580 Oe for x = 0.5) and the x = 0.7 sample does not show any hysteresis loop, however, a field dependent non-linear behavior is noticed. The higher H_C for x = 0.3 sample could be due to the possible existence of large ferromagnetic clusters compared to the other samples. The x = 0.5 sample exhibits M(H) curve typical for a paramagnetic material at 75 K (Fig. 9(c)). Interestingly, the isothermal magnetization recorded at 210, 300 and 320 K for Fe_0.6Cu_0.4Al₂O₄ (Fig. 10) behaves similarly to that observed for x = 0.3 sample at 75 K. An important point is that the M(H) loops exhibit weak hysteresis throughout the measured temperature range (2–320 K), the coercive field values are 800 Oe and 30 Oe at 2 K and 320 K, respectively. The occurrence of hysteresis loop has often been associated with FM interactions in the system. Hence in our measured temperature range we did not reach the paramagnetic state of the systems (x = 0.3 and 0.4). This is also corroborated with the Curie–Weiss plot in the range 2–400 K (not shown here), which is non-linear. The second notable point is that the M(H) loops at 2 and 5 K (Fig. 9(b)) are weak and S-type without clear saturation (up to a field of 5 Tesla), which is akin to spin-glass or superparamagnetic-type system.

Fig. 9 The isothermal magnetization for (a) Fe_0.7Cu_0.3Al₂O₄, (b) Fe_0.6Cu_0.4Al₂O₄, (c) Fe_0.5Cu_0.5Al₂O₄ and (d) Fe_0.3Cu_0.7Al₂O₄ recorded at different temperatures.

Fig. 10 The isothermal magnetization of Fe_0.6Cu_0.4Al₂O₄ recorded at 210 K, 300 K and 320 K.

In order to understand the nature of magnetic interactions in Fe_0.6Cu_0.4Al₂O₄ sample we have carried out ac-susceptibility measurements in the temperature range of 2–300 K. Fig. 11 shows the in phase component of ac data, measured at an applied dc-field of 0 Oe, revealing two distinct frequency dependent behaviors, one at 35 K and the other one above this temperature up to 300 K. In contrast to conventional spin-glass system,³⁴ we have noticed frequency dependency throughout the 2–300 K range, however we have focused our discussion on the low temperature frequency dependent peak at 35 K, which is corresponding to the ZFC cusp. We have further investigated the ac susceptibility measurements at two different applied dc-magnetic fields (H_dc = 100 and 1000 Oe) (Fig. 11(b) and (c)) and we have observed that the frequency dependent behavior of high temperature peak disappears gradually. The high field (H_dc = 1000 Oe) in phase component is similar to the ZFC data (Fig. 8(c)) in the same dc field and the cusp is around 20 K. This shifts to higher temperature with increasing frequency as expected for canonical spin glass system.²³ From Fig. 11, it is also evidenced that the peak position shifts towards lower temperature with the field strength 35 K (H_dc = 0 Oe; H_ac = 10 Oe) to 23 K (H_dc = 1000 Oe; H_ac = 10 Oe). A similar behavior is observed for Fe_0.7Cu_0.3Al₂O₄ sample except the peak around 35 K. Fig. 12 shows the temperature dependent ac-susceptibility for x = 0.3 sample at different frequencies which is similar to that observed for x = 0.4 sample at higher temperatures at H_dc = 0 Oe (Fig. 11(a)). Fig. 13(a) shows the χ′(T) curves at three different frequencies for x = 0.5. The shift in temperature per frequency decade, , suggests that x = 0.5 can be considered as a canonical spin glass system (p ∼ 0.004 to 0.02),^34,35 whereas for the x = 0.7 sample it is not easy to make any conclusion as can be seen from Fig. 13(b).

Fig. 11 The real part of ac-susceptibility, χ′(T), for Fe_0.6Cu_0.4Al₂O₄ at several frequencies and applied dc-field: (a) H_ac = 10 Oe and H_dc = 0 Oe, (b) H_ac = 10 Oe and H_dc = 100 Oe and (c) H_ac = 10 Oe and H_dc = 1000 Oe.

Fig. 12 χ′(T) for Fe_0.7Cu_0.3Al₂O₄ at several frequencies with H_ac = 10 Oe and H_dc = 0 Oe.

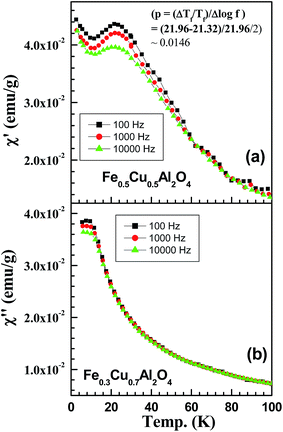Fig. 13 Temperature dependent ac-susceptibility at different frequencies for (a) Fe_0.5Cu_0.5Al₂O₄ and (b) Fe_0.3Cu_0.7Al₂O₄.

The magnetic interaction in Fe_1−xCu_xAl₂O₄ is largely due to the interaction between cation sitting in tetrahedral A-sites. In the spinel structure, the A-site cations form a diamond lattice and the magnetic interaction between the A-site cations is complex involving several paths. The indirect exchange interaction between the A-site cations (Fe/Cu) can be mediated in either of the two ways: (i) (Fe/Cu)²⁺–O–(Fe/Cu)²⁺ path with four nearest-neighbors and (ii) (Fe/Cu)²⁺–O–Al–O–(Fe/Cu)²⁺ path with twelve neighbors. However, the second one is the dominating one, as it has been observed long back in Co₃O₄ where the long exchange path Co²⁺–O–Co–O–Co²⁺ is responsible for the long range antiferromagnetic ordering at 40 K.³⁶ The basic coordination component of the interacting A-site ions is the triangle and results in frustration for the antiferromagnetically coupled sublattice.¹⁶ The observed magnetic behavior may be originated from the defect-induced magnetism phenomenon where defects such as lattice vacancies or local disorder are generated by the reallocation of ions.^37,38 This is the most likely situation in the present case. The smaller size of the particles for x = 0.3 and 0.4 with large surface to volume ratio results in defects induced magnetism. The existence of large coercive field for x = 0.3 and 0.4 samples can be due to the presence of ferromagnetic cluster formation. It has been observed that the microwave synthesized FeAl₂O₄ exhibits formation of magnetic clusters at the grain boundaries due to the inversion effect.¹⁵ A small ferromagnetic moment observed at room temperature in Co₃O₄ was attributed to the inversion of the spinel structure.³⁶ The magnetic behavior of these solid solutions is largely detected by the size of the particle.

Conclusions

To summarize, we have synthesized the Fe_1−xCu_xAl₂O₄ (0.3 ≤ x ≤ 0.8) solid solutions by sol–gel route. The structural and microscopic characterization reveals the formation of nanoparticles of the cubic spinel at 700 °C. The lower copper doped samples are much smaller (6–8 nm) in size compared to the higher doped samples (13–19 nm). The surface elemental composition is fairly similar to the bulk composition. The magnetic properties of these oxides are sensitive to the particle size. The smaller size particles exhibit different behavior compared to the larger sized particles. The large coercive field for the x = 0.3 and 0.4 samples is possibly related to the formation of ferromagnetic clusters. The magnetic cluster formation can be attributed to the inversion and defects induced magnetism. Apart from the x = 0.7 spinel, the other samples exhibit spin glass behavior.

Acknowledgements

Financial support from the Department of Science and Technology, Government of India, by a grant (SR/S1/PC-28/2010) to AG and project fellowship to SM and DST Special Grant to the Department of Chemistry, Jadavpur University in the International Year of Chemistry 2011 is gratefully acknowledged.

References

1. J. C. Lashley, R. Stevens, M. K. Crawford, J. Boerio-Goates, B. F. Woodfield, Y. Qiu, J. W. Lynn, P. A. Goddard and R. A. Fisher, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104406.
2. J. M. A. Almeida, C. T. Meneses, A. S. de Menezes, R. F. Jardim and J. M. Sasaki, J. Magn. Magn. Mater., 2008, 320, e304–e307.
3. H. Ishibashi and T. Yasumi, J. Magn. Magn. Mater., 2007, 310, e610–e612.
4. J. L. Soubeyroux, D. Fiorani and E. Agostinelli, J. Magn. Magn. Mater., 1986, 54–57, 83–84.
5. P. Jeevanandam, Y. Koltypin and A. Gedanken, Mater. Sci. Eng., B, 2002, 90, 125–132.
6. S. J. Byrne, S. A. Corr, Y. K. Gun'ko, J. M. Kelly, D. F. Brougham and S. Ghosh, Chem. Commun., 2004, 22, 2560–2561.
7. S. A. Corr, Y. K. Gun'ko, A. P. Douvalis, M. Venkatesan and R. D. Gunning, J. Mater. Chem., 2004, 14, 944–946.
8. L. F. Liotta, G. di Carlo, G. Pantaleo and G. Deganello, Appl. Catal., B, 2007, 70, 314–322.
9. H. J. Nam, T. Sasakiand and N. Koshizaki, J. Phys. Chem. B, 2006, 110, 23081–23084.
10. J. W. Kim, P. W. Shin, M. J. Lee and S. J. Lee, J. Ceram. Process. Res., 2006, 7, 117–121.
11. W. D. Fei, M. Hu and C. K. Yao, Mater. Chem. Phys., 2003, 77, 882–888.
12. S. Sheibani and M. F. Najafabadi, Mater. Des., 2007, 28, 2373–2378.
13. D. P. Dutta and G. Sharma, Mater. Sci. Eng., B, 2011, 176, 177–180.
14. P. M. Botta, R. C. Mercader, E. F. Aglietti and J. M. Porto López, Scr. Mater., 2003, 48, 1093–1098.
15. J. Fukushima, Y. Hayashi and H. Takizawa, Journal of Asian Ceramic Societies, 2013, 1, 41–45.
16. N. Tristan, J. Hemberger, A. Krimmel, H. A. Krug von Nidda, V. Tsurkanand and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(1–9), 174404.
17. U. Russo, S. Carbonin and A. D. Giusta, in Mossbauer Spectroscopy Applied to Magnetism and Materials Science, ed. G. J. Long and F. Grandjean, Plenum, New York, 1996, vol. 2, p. 207.
18. R. Mistri, S. Maiti, J. Llorca, M. Dominguez, T. K. Mandal, P. Mohanty, B. C. Ray and A. Gayen, Appl. Catal., A, 2014, 485, 40–50.
19. J. Yanyan, L. Jinggang, S. Xiaotao, N. Guiling, W. Chengyu and G. Xiumei, J. Sol–Gel Sci. Technol., 2007, 42, 41–45.
20. M. Salavati-Niasari, F. Davarand and M. Farhadi, J. Sol–Gel Sci. Technol., 2009, 51, 48–52.
21. L. A. Fenner, A. S. Wills, S. T. Bramwell, M. Dahlberg and P. Schiffer, J. Phys.: Conf. Ser., 2009, 145, 012029.
22. J. Rodriguez-Carvajal, An Introduction to the Program FULLPROF 2000, Laboratoire Léon Brillouin, CEA-CNRS, Saclay, France, 2001.
23. S. Aravazhi, PhD Thesis, Pondicherry University, 2002, (Acc. No.: 002728), p. 171.
24. B. D. Cullity and S. R. Stock, Elements of X-Ray Diffraction, Prentice-Hall Inc., 3rd edn, 2001.
25. J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bombem, in Handbook of X-ray Photoelectron Spectroscopy, ed. J. Chastain, Perkin-Elmer Corporation, Eden Prairie, USA, 1992, p. 87.
26. M. Sreedhar, I. N. Reddy, P. Bera, D. Ramachandran, K. G. Saravanan, A. M. Rabel, C. Anandan and P. Kuppusami, Appl. Phys. A, 2015, 120, 765–773.
27. S. Hüfner, in Photoelectron Spectroscopy: Principles and Applications, Springer, 3rd edn, 2003, p. 109.
28. D. C. Frost, A. Ishitani and C. A. McDowell, Mol. Phys., 1974, 24, 861–877.
29. G. Moretti, G. Fierro, M. Lo Jacono and P. Porta, Surf. Interface Anal., 1989, 14, 325–336.
30. Y. Okamoto, K. Fukino, T. Imanaka and S. Teranishi, J. Phys. Chem., 1983, 87, 3740–3747.
31. T. Mathew, N. R. Shiju, K. Sreekumar, B. S. Rao and C. S. Gopinath, J. Catal., 2002, 210, 405–417.
32. K. Lim, J. Park, D.-G. Kim, J.-K. Kim, J.-W. Kang and Y.-C. Kang, Appl. Surf. Sci., 2012, 258, 9054–9057.
33. G. A. C. Rodriguez, G. G. Guillen, M. I. M. Palma, T. K. D. Roy, A. M. G. Hernandez, B. Krishnan and S. Shaji, Int. J. Appl. Ceram. Technol., 2015, 12, E34–E43.
34. A. J. Mydosh, Spin Glasses: An Experimental Introduction, Taylor and Francis, London, 1993.
35. Y. Bréard, V. Hardy, B. Raveau, A. Maignan, H.-J. Lin, L.-Y. Jang, H. H. Hsieh and C. T. Chen, J. Phys.: Condens. Matter, 2007, 19, 216212.
36. B. Raveau and Md. M. Seikh, Cobalt Oxides, Wiley-VCH, 2012.
37. O. V. Yazyev, Rep. Prog. Phys., 2010, 73, 056501.
38. S. B. Ogale, Adv. Mater., 2010, 22, 3125–3155.

---