Simultaneous extraction and preconcentration of some metal ions using eucalyptus-wood based activated carbon modified with silver hydroxide nanoparticles and a chelating agent: optimization by an experimental design†
Maryam Rajabi*a,
Alireza Rezaiea and
Mehrorang Ghaedib
aDepartment of Chemistry, Semnan University, Semnan 35195-363, Iran. E-mail: mrajabi@semnan.ac.ir
bChemistry Department, Yasouj University, Yasouj 75918-74831, Iran
First published on 9th October 2015
Abstract
In the present work, the solid phase extraction (SPE) of Cr(III), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) metal ions was carried out using a new adsorbent, activated carbon modified with silver hydroxide nanoparticles and a chelating agent. The activated carbon was produced by the acid treatment of the carbon obtained from eucalyptus wood. The effects of different parameters on the metal ion preconcentrations were studied and optimized by a central composite experimental design, which is one of the most applicable response surface methodologies used in the design of experiments. The four major variables affecting the adsorption process, consisting of the pH value, amount of adsorbent, amount of ligand, and flow rate of the sample solution, were optimized. In the desorption process, the volume, concentration, and flow rate of the eluting solvent were considered as the variables affecting the amount of metal ion preconcentration. At the end of each step, the metal ions were quantified by flame atomic absorption spectrometry (FAAS). Under the optimal conditions, the recovery percentage and enrichment factor for all the metal ions under study were higher than 98% and 100, respectively (except for the Ni(II) ion, with an enrichment factor of 83.6), which indicate the high performance of the presented preconcentration method. Also, the detection limits for the Cr(III), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) ions were found to be 4.7, 3, 4, 1.7, 1.6, and 2.3 μg L−1, respectively. The relative standard deviation values for six replicate measurements of 0.2 mg L−1 of each metal ion were lower than 2.62%. Thus this preconcentration method can have a high accuracy and precision in the determination of trace amounts of potentially toxic metal ions.
1. Introduction
Any metal that possesses adverse effects in trace amounts may be potentially toxic. Hence, the design and development of novel protocols and use of proper tools for the identification and monitoring of toxic metals are urgent requirements. It should be noted that certain potentially toxic metals such as cadmium, cobalt, and lead can be either harmful or essential, depending on their levels. Cadmium is known to accumulate in the human kidneys for a relatively long time (20–30 years), while in high doses it produces adverse effects on the respiratory system and also leads to bone diseases. Humans normally absorb cadmium into their bodies by either ingestion or uptake through the skin.1 Lead poisoning, except at a level lower than the threshold limit, causes serious damage to human health; it has also been proven to be a carcinogenic agent. Cobalt compounds are extensively applied as catalysts in organic reactions and various industries such as paints, lacquers, varnishes, and printing inks as drying agents, and in alloying with other metals. The presence of cobalt leads to a reduction in the iron absorption, in particular, for patients suffering from iron deficiency.2 Aspiration of the nickel derivatives can lead to serious problems, including the lung and dermatological diseases and malignant tumors. Moreover, nickel can cause a skin disorder known as nickel-eczema, which is a considerable health problem among women.3 Chromium and its compounds have a diverse usage in the metal alloys, and as pigments for rubber, paints, and paper, while their high contents are harmful to most organisms.4 Copper is an essential mineral for the mental and physical health, in despite of the fact that its higher content deposits in the liver and disrupts its ability to detoxify; it also adversely affects on the nervous and reproductive systems. Therefore, it is important to monitor trace levels of these metals in environmental samples.Many established analytical techniques such as electrothermal atomic absorption spectrometry (ETAAS),5 inductively coupled plasma-mass spectrometry (ICP-MS),6 inductively coupled plasma-optical emission spectrometry (ICP-OES),7 atomic fluorescence spectrometry (AFS), X-ray fluorescence spectrometry (XRF), and atomic absorption spectrometry (AAS),8 with good detection limits and high accuracies, are used for monitoring and quantification of the understudied analytes at trace levels.9 However, their very low concentrations in environmentally complex matrices encourage and make an emphasis on the researchers, especially analytical chemists, to preliminary apply the preconcentration techniques10–13 that sometimes are associated with preconcentration as well as separation. Good reports in the literature for such a purpose have been based upon the applications of liquid–liquid extraction, ion-exchange procedures, membrane filtration, cloud point extraction, electro-analytical techniques, and solid phase extraction (SPE). Among these sample preparation methods, advantages like simplicity, rapidity, and the ability to attain a high preconcentration factor candidate SPE based on different and versatile sorbents (activated carbon, C-18, C-60, C-70, Diaion HP-20, chelating resins, and silica gel) as a unique protocol to improve the method characteristics.
Availability of low-cost resources such as plant residues, and suitable properties like high porosity, and large surface area are valuable benefits for the activated carbon used in SPE.14,15 Also its properties, both the selectivity and the adsorption efficiency, can be improved by physical or chemical modifications. The conventional and extensive protocols used for the modification are acid treatment, oxidization, ammonization, and microwave treatment.16–20 The excellent surface properties obtained via chemical modifications lead to its improved binding to nanomaterials in order to achieve a high-performance separation. In fact, the nanomaterials, including nanoparticles, nanowires, nanotubes, and nanocapsules, provide better kinetics and greater extraction capacities in the uptake of metal ions due to their unique physical and chemical properties such as high dispensability and high surface-to-volume ratio. Also, the use of chelating agents causes to improve the selectivity of the metal ions adsorptions.21–26
The experimental design has been accepted to be a beneficial procedure in the modeling and simultaneous optimization of the variables affecting SPE. Also, it may cause to enhance the optimum response values.27–29 Moreover, this procedure can identify the main variables among a high number of them; therefore, more time and expense can be saved before the optimization process.30–32 Among the various types of experimental designs, the response surface methodologies have commonly been applied for the optimization of the effective variables.33–35 They mainly include the central composite design (CCD), Box-Behnken design (BBD), and Doehlert design. In fact, these second-order designs, which are combinations of the mathematical and statistical methods, optimize efficiently the main variables of the process through fitting of the experimental data to the quadratic surfaces.36,37
In this work, the silver hydroxide nanoparticles loaded on the activated carbon was synthesized, and, subsequently, modified with N,N′-bis(salicylidene)-2,2′-dimethyl-1,3-propanediimine (SMPA), as a chelating agent. At a later stage, this novel adsorbent was utilized for the separation and preconcentration of the Cr(III), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) ions in various matrices. The larger pores and various surface functional groups lead to greater uptakes of the metallic cations. A central composite experimental design was used to find the optimum conditions in combination with the desirability function. Finally, the proposed extraction and preconcentration method was successfully applied to the determination of metal ions in real samples by FAAS with satisfactory results.
2. Experimental
2.1. Materials
All the chemicals used including HNO3, HCl, NaOH, ethanol, and the salts of Cr(NO3)3·9H2O, Cu(NO3)2·3H2O, NiSO4·6H2O, Cd(NO3)2·4H2O, Co(NO3)2·6H2O, and AgNO3 with analytical grade and the highest purity available were purchased from Merck (Germany). Eucalyptus wood, as a precursor in the preparation of the activated carbon, was obtained from the Semnan province in Iran.2.2. Instrumentation
An Agilent 200 Series AA (model 240 AA) flame atomic absorption spectrometer (USA) including air-acetylene flame and simultaneous four hollow cathode lamps was used for the metal ion determination. The instrumental parameters were adjusted as follow:Wavelength: Pb, 217.0 nm (slit width: 1.0 nm); Cd, 228.8 nm (slit width: 0.5 nm); Co, 240.7 nm (slit width: 0.2 nm); Cr, 357.9 nm (slit width: 0.2 nm); Ni, 232.0 nm (slit width: 0.2 nm); Cu, 324.7 nm (slit width: 0.5 nm); and lamp current, 10.0 mA.
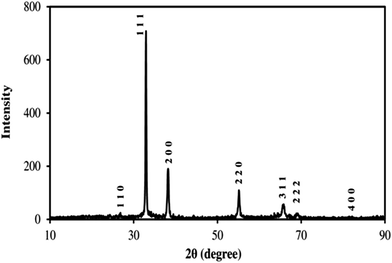
A Shimadsu, UV-visible 1650 PC spectrophotometer (Japan) was used to measure the absorbance spectra in order to follow the deposition of the ligand onto the adsorbent. A BEL PHS-3BW pH-meter (Italy) with a combined glass-Ag/AgCl electrode was used for adjustment of the solution pH values. The FT-IR spectra were recorded on a Shimadzu 8400 double-beam spectrophotometer (Japan) in the range of 4000–400 cm−1, with KBr pallets containing a very small amount of the eucalyptus-based carbon, before and after modification with acid. A scanning electron microscopy (SEM) (LEO, model VP 1450, Germany) was used to identify the surface morphologies of the activated carbon and silver hydroxide nanoparticles loaded on the activated carbon. The X-ray diffraction (XRD) patterns were collected using an automated Philips X'Pert X-ray diffractometer with Cu Kα radiation (40 kV and 30 mA) for 2θ values over 10–90° in order to identify the chemical structure of the AgOH nanoparticles.
2.3. Preparation of real samples
In order to prepare the different real samples, various pretreatments were carried out, as follow:Green tea sample: after placing 1.00 g of the sample in a beaker, 25 mL of boiled distilled water was added to infuse for 20 min. The mixture was then filtered, and certain amounts of the understudied metal ions were spiked to the residual solution.38
Meat sample: 5 g of cow meat was weighted accurately. After adding 20–25 mL of concentrated H2SO4 and standing for several minutes, it was digested with 4 mL of concentrated HNO3 and 2 mL of concentrated H2O2 in a microwave system. Then, the volume of the digested sample was made up to 250 mL with distilled water, followed by spiking with certain amounts of the understudied metal ions.39
Fruit sample: a 10 g peach in a silica crucible was heated for 3 h on a hot plate, and the charred material was then transferred to a furnace for overnight, heating it at 650 °C. The residue obtained was cooled, treated with 10 mL of concentrated nitric acid and 3 mL of 30% (w/v) H2O2, and again kept in the furnace for 2 h. The final residue was treated with 3 mL of concentrated hydrochloric acid and 2–4 mL of 70% (w/v) perchloric acid, and evaporated to fumes. The resulting solution was filtered and spiked with certain amounts of the understudied metal ions.
Tap and well waters: after filtering, certain amounts of the metal ions were spiked to the residual solutions.
Finally, the preconcentration procedure given in Section 2.7 was applied to the prepared solutions.
2.4. Preparation of activated carbon
After crushing the pruned branches of a number of eucalyptus trees into small pieces, they were washed with distilled water to remove the dirt particles and water-soluble materials, and then dried overnight in an oven at 80 °C. The dried small pieces of eucalyptus wood in closed crucibles were placed in a furnace and heated at 350 °C for 2 h. Then, the resulting charcoals were withdrawn from the furnace and cooled to room temperature. After further grinding in a mortar, they were sieved into a uniform size (80–100 mesh). Then, they were impregnated in a concentrated solution of the HCl and HNO3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for 24 h with a mass ratio equal to 1
1) for 24 h with a mass ratio equal to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. The acidity of the activated carbon was removed simply by several washings with distilled water, and, subsequently, it was kept in an oven at 110 °C for 24 h.
4. The acidity of the activated carbon was removed simply by several washings with distilled water, and, subsequently, it was kept in an oven at 110 °C for 24 h.
2.5. Synthesis of silver hydroxide nanoparticles and ligand
AgOH nanoparticles were synthesized by the precipitation method.40 Firstly, 10 g of AgNO3 was dissolved in 100 mL of deionized water. After a continuous stirring for 2 min, the aqueous solution obtained was exposed to the ultrasound waves, and, simultaneously, NaOH solution (0.05 mg L−1) was added dropwise to the solution. Finally, the AgOH nanoparticles produced were washed thoroughly with deionized water, followed by drying in air at 70 °C for 12 h.The ligand N,N′-bis(salicylidene)-2,2′-dimethyl-1,3-propanediimine (SMPA) was synthesized according to a method reported in the literature.41 2,2-Dimethyl-1,3-propanediamine (2.4 mL, 20 mmol) was added to a boiling solution of salicylaldehyde (4.3 mL, 40 mmol) in 50 mL of ethanol, causing a color change from colorless to yellow. About one-third of the solvent was removed under reduced pressure, initiating the formation of yellow crystals. When the crystal formation ended, the product was filtered and dried.
2.6. Modification of activated carbon with silver hydroxide nanoparticles and ligand
Firstly, the physical modification of the activated carbon surface was carried out by mixing it with the silver hydroxide nanoparticles in a mass ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Then, for creation of selectivity towards the metal ions under study, a certain amount of the ligand was dissolved in ethanol, and added to the silver hydroxide nanoparticles loaded on the activated carbon.
1. Then, for creation of selectivity towards the metal ions under study, a certain amount of the ligand was dissolved in ethanol, and added to the silver hydroxide nanoparticles loaded on the activated carbon.
2.7. Sorption and elution steps
The extraction of the understudied metal ions from their aqueous solutions and their preconcentrations were evaluated by a continuous (column) system as follows:At first, the column was packed with the adsorbent composed of a fixed value of the silver hydroxide nanoparticles loaded on the activated carbon. Then a certain volume of the ligand solution with a pre-determined concentration was passed through the column. Finally, an aliquot of 50 mL of the initial sample solution (0.2 mg L−1 of each metal ion) was applied.
Subsequently, various runs were conducted accordingly to the preliminary experiments designed using CCD at various pH values adjusted by the dropwise addition of 0.1 mol L−1 of the nitric acid and/or sodium hydroxide solutions. Then, the concentrations of the residual metal ions present in the solutions were determined by FAAS.
The extraction percentage for each metal ion was calculated as:
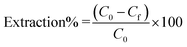 | (1) |
In the elution stage, according to the secondary CCD, certain concentrations and volumes of the eluting solvent with specified flow rates (the effective parameters in the elution step), were passed through the column to recover the metal ions adsorbed in the previous step. The eluted metal ions were introduced to FAAS in order to determine the adsorbed amount of each metal ion.
The recovery percentage for each metal ion was calculated as:
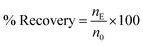 | (2) |
2.8. Experimental design methodology
In order to reduce the required time and number of trials, an appropriate experimental design allowing simultaneous variations in all the experimental factors was applied to achieve the real and enhanced optimum conditions. The central composite design (CCD) is one of the most popular classes of the second-order designs in the experimental design. It was firstly introduced by Box and Wilson in 1951, and it is well-suited for fitting a quadratic surface, so that; it usually works well for the optimization process.42In this work, the Design-expert 7.0.0 Software package was used for the analysis of the experimental data and calculating the response equations in terms of the main and effective factors.
3. Results and discussion
3.1. Characterization of adsorbent
In order to study the surface functional groups created on the eucalyptus wood-based carbon by acid treatment, the FT-IR spectra of carbon, taken after and before impregnating in a concentrated solution of HCl and HNO3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), were studied in the range of 4000–400 cm−1 (Fig. 1a and b). In Fig. 1a, the broad band in the range of 3300–3750 cm−1 was assigned to the stretching vibration of the hydroxyl functional group. In addition, the bands at about 1720 and 1230 cm−1 probably correspond to the C
1), were studied in the range of 4000–400 cm−1 (Fig. 1a and b). In Fig. 1a, the broad band in the range of 3300–3750 cm−1 was assigned to the stretching vibration of the hydroxyl functional group. In addition, the bands at about 1720 and 1230 cm−1 probably correspond to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–O stretching vibrations, respectively. These three peaks were created due to the carbon surface reaction with the concentrated solution of HCl and HNO3 (1
O and C–O stretching vibrations, respectively. These three peaks were created due to the carbon surface reaction with the concentrated solution of HCl and HNO3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), which were not seen in Fig. 1b.
1), which were not seen in Fig. 1b.
 | ||
Fig. 1 (a and b) FT-IR spectra for carbon produced from eucalyptus wood, after and before impregnating in a concentrated solution of HCl and HNO3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), respectively. 1), respectively. | ||
The X-ray pattern for the silver hydroxide nanoparticles is shown in Fig. 2. The diffraction peaks for the silver hydroxide nanoparticles were appeared at the Bragg angles of about 26.6°, 31.1°, 39.0°, 52.6°, 68.9°, 69.8°, and 83.0°, ascribed to the (110), (111), (200), (220), (311), (222), and (400) crystal planes, respectively. The X-ray investigations indicated a cubic lattice structure for the AgOH nanoparticles. The average size of the silver hydroxide nanoparticles was calculated from the main peak (111) using the Scherrer equation. The results obtained indicated that the average size of the silver hydroxide nanoparticles was about 45 nm.
The surface morphologies of the activated carbon and silver hydroxide nanoparticles loaded on the activated carbon were characterized by scanning electron microscopy (SEM) (Fig. 3a and b). By studying the SEM related to Fig. 3a, an irregular activated carbon surface can be observed. As shown in Fig. 3b, the adsorbent surface is more uniform, with a high surface area; due to the loading of the silver hydroxide nanoparticles on the activated carbon.
In order to confirm the immobilization of the ligand on the adsorbent, firstly, the UV-visible absorbance spectrum of the ligand solution (0.001 mol L−1) was taken (Fig. 3c). In the next step, 10 mL of this solution was added to 0.1 g of the adsorbent, and the resulting mixture was placed on a stirrer for 3 h. It was then filtered and centrifuged, and the UV-visible absorbance spectrum of the filtered solution was taken again (Fig. 3d). The absorbance reduction of the ligand peak, shown in this figure, showed that the ligand was somehow linked to the adsorbent via coordinance bonds with the AgOH nanoparticles existing on the carbon surface.
The porosity and effective surface area measurements for the silver hydroxide nanoparticles loaded on the activated carbon were performed by the N2 equilibrium adsorption isotherms at 77 K (Table 1). The BET surface area of the adsorbent used was 1291.94 m2 g−1, with a pore volume of 0.6434 cm3 g−1. Also the average pore width and particle size were found to be 19.92 and 46.44 Å, respectively, indicating an appreciable narrow micro-porosity for silver hydroxide nanoparticles loaded on the activated carbon.
| SBET (m2 g−1) | Sext (m2 g−1) | Smic (m2 g−1) | Vt (cm3 g−1) | Vmic (cm3 g−1) | Dp (Å) |
|---|---|---|---|---|---|
| a SBET: BET surface area; Sext: external surface area; Smic: micropore surface area; Vt: total pore volume; Vmic: micropore volume; Dp: average particle size. | |||||
| 1291.94 | 679.92 | 612.02 | 0.6434 | 0.2700 | 46.44 |
It is necessary to explain, the probable mechanism for modification of the activated carbon with the AgOH nanoparticles and ligand can be proposed as follows: the hydroxyl group in AgOH can bind the activated carbon via hydrogen bonding to the hydroxide, carboxylic or carbonyl groups. Moreover, silver, as a d10 soft atom, can bind through ion–dipole interactions to the non-localized pi-electrons of the carbon backbone. On the other hand, the silver ions can be coordinated to the iminic nitrogen and phenoxy oxygen atoms in the ligand. The oxygen atoms in the ligand can also interact with Ag+ through ion–dipole interactions.43
3.2. Optimization of preconcentration procedure by RSM approach
The optimization of the metal ion uptakes on the adsorbent was carried out using CCD. The four main variables affecting the adsorption step (initial sample pH value, solution flow rate, and amounts of the adsorbent and ligand) were tabulated in Table 2.| Factors | Levels | ||||
|---|---|---|---|---|---|
| −α | Low (−1) | Central (0) | High (+1) | +α | |
| A: amount of adsorbent (g) | 0.050 | 0.075 | 0.100 | 0.125 | 0.150 |
| B: amount of ligand (g) | 0.008 | 0.016 | 0.024 | 0.032 | 0.040 |
| C: solution flow rate (mL min−1) | 1.00 | 1.38 | 1.75 | 2.13 | 2.50 |
| D: pH | 4 | 5 | 6 | 7 | 8 |
As shown in this table, the amounts of the variables involved in the preconcentration procedure were extended in five levels, −α to +α, where α; represents the number of axial points (star points), and depends on the number of factors (k). The α value, in a full factorial state, was evaluated by the following relation:44
| α = [2k]1/4 | (3) |
The α value was equal 2 for the four factors affecting the adsorption step.
The total number of experiments in CCD can be calculated as:45
| N = 2k + 2k + nc | (4) |
For predicting the optimal conditions, a second-order polynomial model between the main variables and the response can be expressed as:
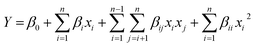 | (5) |
| YCr(III) = −165.86 + 1148.3A + 28.65B + 59.8C + 3.3D + 458.3BD − 3.7CD − 1950A2 − 4.72C2 | (6) |
| YCu(II) = −231 + 1793A + 2701B + 44.3C + 11.2D − 160AD + 3.7CD − 3483A2 − 13509B2 − 4.6C2 − 7.93D2 | (7) |
| YPb(II) = −229 + 1849A + 2538B + 44.55D + 1.6CD − 8308A2 − 47933B2 − 4.6C2 − 17.4D2 | (8) |
| YNi(II) = −330.4 + 2236.7A + 67.21C + 158.3D + 175AC + 547BC − 1458BD − 12.7CD − 13867A2 − 7.04C2 | (9) |
| YCd(II) = −254.4 + 1818A + 1733.1B + 86.3C − 23.3D − 5156.3AB + 36.3AC + 190AD + 168BC + 3.75CD − 10525A2 − 38330B2 − 8.6C2 − 8.6D2 | (10) |
| YCo(II) = −303.7 + 1163A + 671.9B + 29.9D + 15000AB − 281.3BC − 500BD − 3233A2 − 33528.6B2 − 6.9C2 − 8.2D2 | (11) |
| Source of variation | Sum of squares | Degree of freedom | Mean square | F-value | P-value |
|---|---|---|---|---|---|
| Pb(II) | |||||
| Model | 2268.7 | 14 | 162.1 | 179.77 | <0.0001 |
| Residual | 13.52 | 15 | 0.90 | ||
| Lack of fit | 12.19 | 10 | 1.22 | 4.57 | 0.0527 |
| Pure error | 1.33 | 5 | 0.27 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cd(II) | |||||
| Model | 4122.2 | 14 | 294.45 | 172.50 | <0.0001 |
| Residual | 25.60 | 15 | 1.71 | ||
| Lack of fit | 22.77 | 10 | 2.28 | 4.02 | 0.0690 |
| Pure error | 2.83 | 5 | 0.57 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Co(II) | |||||
| Model | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268 268 |
14 | 1233.4 | 1345.5 | <0.0001 |
| Residual | 13.75 | 15 | 0.92 | ||
| Lack of fit | 12.42 | 10 | 1.24 | 4.66 | 0.0517 |
| Pure error | 1.33 | 5 | 0.27 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cu(II) | |||||
| Model | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 668 668 |
14 | 1047 | 1199.3 | <0.0001 |
| Residual | 13.10 | 15 | 0.87 | ||
| Lack of fit | 11.77 | 10 | 1.18 | 4.41 | 0.0575 |
| Pure error | 1.33 | 5 | 0.27 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cr(III) | |||||
| Model | 8465.9 | 14 | 604.71 | 440.86 | <0.0001 |
| Residual | 20.58 | 15 | 1.37 | ||
| Lack of fit | 18.58 | 10 | 1.86 | 4.65 | 0.0519 |
| Pure error | 2.00 | 5 | 0.40 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Ni(II) | |||||
| Model | 8915.2 | 14 | 636.80 | 21.20 | <0.0001 |
| Residual | 450.67 | 15 | 30.04 | ||
| Lack of fit | 372.67 | 10 | 37.27 | 2.39 | 0.1743 |
| Pure error | 78.00 | 5 | 15.60 | ||
Using the determination coefficient, R2 values, the quality of the fitted polynomial models were expressed. The R2 values show a measure of how much variability in the response values obtained can be explained by the experimental factors and their interactions. The values for R2 and Adj-R2 for all of the metal ions were found to be higher 0.90, and close to each other. This indicates the high accuracy and reliability of the proposed models in the determination of the response values.
3.2.1.1. Interaction effects of process variables. Some of the effects of the interactions between the process variables on the extraction percentages of the metal ions, according to their significant P-values, were visualized through the 3D views of the response surface plots (some of the important response surface plots are shown in Fig. 4). The extraction percentages of the metal ions increased with the increment of the amounts of the adsorbent and ligand, while they decreased with increase in the solution flow rate (after passing a maximum). A higher amount of the adsorbent provided a greater surface in order to adsorb the metal ions, which caused to improve the adsorption capacity. Also, an increase in amount of ligands enhanced the selectivity of metal ion extractions and the adsorption capacity. The decrease in the extraction percentages of the metal ions at higher solution flow rates may be due to the decrease in the contact time of the adsorbent sites with the metal ions. Also, lower solution flow rates caused to the increase the metal ion adsorption times. By increasing the solution pH, the extraction of the metal ions improved due to the reduction in the competition between the H+ ions and metal ions in the adsorption on the adsorbent. However, at an alkaline pH, the metal cations probably participate, which leads to a reduction in the metal ion extractions.
3.2.1.2. Optimization of CCD using desirability function. The optimum conditions obtained using the desirability function in the adsorption step were found to be 0.12 g of the silver hydroxide nanoparticles loaded on the activated carbon, 0.03 g of the ligand, 1.38 mL min−1 of the solution flow rate, and the pH value of 5.73, which resulted in maximum extraction percentages (96.16, 96.72, 99.13, 98.55, 88.96, and 93% for the Cr(III), Cu(II), Pb(II), Ni(II), Cd(II) and Co(II) ions, respectively) with a high desirability value of 0.964. Three experiments were performed based on the optimum conditions obtained using the desirability function. The average values for the extraction percentages of the metal ions and the corresponding values predicted by the software had low differences, which could be ignored. Thus the optimum responses obtained had a high accuracy and precision.
3.3. Statistical evaluation of desorption step
After choosing HNO3 as a proper eluting solvent among the applied eluents viz. HCl, HNO3, H2SO4, and CH3COOH through the one-at-a-time method, the optimization of the metal ion desorptions was carried out using CCD. The three main variables affecting the desorption step (concentration, volume, and flow rate of the eluting solvent) and their levels, −1.86 to +1.86, were indicated in Table 4. The recovery percentages obtained from 20 desorption step runs (calculated by eqn (2)) were tabulated in Table S2 (see the ESI†).| Factors | Levels | ||||
|---|---|---|---|---|---|
| −α | Low (−1) | Central (0) | High (+1) | +α | |
| A: eluent volume (mL) | 1.98 | 3.00 | 4.49 | 5.98 | 7.00 |
| B: eluent concentration (mol L−1) | 0.98 | 2.00 | 3.49 | 4.98 | 6.00 |
| C: flow rate of elution (mL min−1) | 0.53 | 0.90 | 1.45 | 2.00 | 2.38 |
The experimental data obtained from the secondary experimental design, which followed the optimum values for the adsorption step, for the three main effective factors in the elution step including the concentration, volume, and flow rate of the eluting solvent were evaluated by ANOVA (Table 5). Similar to the “statistical evaluation of adsorption step” section, based on the P-values in 95% of significance level, the significance of the models was identified. The quadratic models obtained for the recovery percentages of the metal ions in terms of uncoded factors were reported in eqn (12)–(17) for the Cr(III), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) ions, respectively.
| YCr(III) = −114.2 + 24.2A + 19.2B + 48.1C + 0.96AB − 10.2AC − 4.4BC − 1.1B2 − 3.24C2 | (12) |
| YCu(II) = −27.96 + 18.5A + 14.2B − 18.0C + 0.5AB − 1.53AC − 3.2BC − 1.53A2 + 0.6B2 + 4.0C2 | (13) |
| YPb(II) = +8.43 + 9.95A + 16.02B − 4.42C + 0.30AB − 0.76AC − 1.37BC − 1.50B2 − 1.5C2 | (14) |
| YN(II) = −42.3 + 17.64A − 0.69B + 17.44C + 2.31AB − 8.70AC | (15) |
| YCd(II) = −6.71 + 14.33A + 22.5B − 15.20C − 0.44A2 − 2.04B2 | (16) |
| YCo(II) = −38.62 + 24.50A + 23.53B + 3.52C + 0.45AB − 1.83AC − 3.66BC − 1.30A2 − 2.2B2 − 4.2C2 | (17) |
| Source of variation | Sum of squares | Degree of freedom | Mean square | F-value | P-value |
|---|---|---|---|---|---|
| Pb(II) | |||||
| Model | 5567 | 9 | 618.6 | 375.12 | <0.0001 |
| Residual | 16.49 | 10 | 1.65 | ||
| Lack of fit | 13.61 | 5 | 2.72 | 4.74 | 0.0565 |
| Pure error | 2.88 | 5 | 0.57 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cd(II) | |||||
| Model | 5567 | 9 | 618.6 | 375.1 | <0.0001 |
| Residual | 16.491 | 10 | 1.6491 | ||
| Lack of fit | 13.616 | 5 | 2.7233 | 4.7361 | 0.05651 |
| Pure error | 2.875 | 5 | 0.575 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Co(II) | |||||
| Model | 7315.6 | 9 | 812.85 | 1129.9 | <0.0001 |
| Residual | 7.19 | 10 | 0.72 | ||
| Lack of fit | 5.69 | 5 | 1.14 | 3.80 | 0.0848 |
| Pure error | 1.50 | 5 | 0.30 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cu(II) | |||||
| Model | 1922.8 | 9 | 1214 | 1042.5 | <0.0001 |
| Residual | 11.64 | 10 | 1.16 | ||
| Lack of fit | 9.64 | 5 | 1.93 | 4.82 | 0.0546 |
| Pure error | 2.00 | 5 | 0.40 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Cr(III) | |||||
| Model | 1168 | 9 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 975 |
871.67 | <0.0001 |
| Residual | 14.90 | 10 | 1.49 | ||
| Lack of fit | 12.06 | 5 | 2.41 | 4.26 | 0.0689 |
| Pure error | 2.83 | 5 | 0.51 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Ni(II) | |||||
| Model | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595 595 |
9 | 1177.2 | 415.18 | <0.0001 |
| Residual | 28.354 | 10 | 2.8354 | ||
| Lack of fit | 25.521 | 5 | 5.1041 | 9.0073 | 0.0553 |
| Pure error | 2.8333 | 5 | 0.5666 | ||
The R2 and Adj-R2 values for all of metal ions were found to be higher than 0.98. The high amounts of R2 (proximity to unity), and being close to the amounts of Adj-R2 indicate the high accuracy and reliability of the proposed models in the determination of the response values.
3.4. Effect of breakthrough volume
The sample volume is one of the important parameters affecting the preconcentration factor in the analysis of real samples. The breakthrough volumes of the sample solutions for the metal ions were investigated using 250–1500 mL model solutions containing 0.2 mg of each metal salt in a SPE system under the optimized experimental conditions. The results obtained demonstrated that the dilution effect was not significant for the sample volumes up to 1000, 1000, 1000, 1000, 750, and 500 mL for the Cr(II), Cu(II), Pb(II), Cd(II), Co(II) and Ni(II) ions, respectively. Therefore, preconcentration factors for the new adsorbent were found to be 167.22, 167.22, 167.22, 167.22, 125.4, and 83.6 for these ions, respectively.3.5. Effect of potentially interfering ions
To investigate the effects of the potentially interfering ions found in natural samples, various cations and anions were added to 200 mL of a solution containing 0.2 mg of each metal salt. The degrees of tolerance for the potentially interfering ions are presented in Table 6. From the tolerance results, it can be seen that even high levels of the potentially interfering ions have no impact on the preconcentration of these metal ions at pH 5.73. Thus the SPE preconcentration method can be more efficient in the determination of these potentially toxic metal ions in complicated matrices.| Potentially interfering ions | Tolerance limita (Ci/Ca) | Recovery (%) ± standard deviation (N = 3) | |||||
|---|---|---|---|---|---|---|---|
| Cr(III) | Cu(II) | Pb(II) | Ni(II) | Cd(II) | Co(II) | ||
| a Concentration ratio of potentially interfering and analyte ions, adsorption conditions: 0.12 g of adsorbent, 0.03 g of ligand, 1.38 mL min−1 of solution flow rate, pH = 5.73 and 200 mL of the sample with concentration of 0.2 mg L−1 for Cr(III), Cu(II), Pb(II), Ni(II), Cd(II) and Co(II) ions. Desorption conditions: 5.98 mL of HNO3 with the concentration of 4.98 mol L−1 and elution flow rate of 0.90 mL min−1. | |||||||
| Na+ | 1000 | 98.0 ± 1.8 | 90.0 ± 2.0 | 99.0 ± 2.0 | 98.0 ± 1.0 | 98.0 ± 1.0 | 93.0 ± 2.0 |
| K+ | 1000 | 98.0 ± 1.2 | 91.0 ± 2.0 | 99.0 ± 2.0 | 97.0 ± 1.9 | 98.0 ± 2.0 | 94.0 ± 1.3 |
| Ag+ | 750 | 97.0 ± 2.0 | 92.0 ± 1.8 | 98.0 ± 1.3 | 98.0 ± 1.8 | 97.0 ± 2.0 | 94.0 ± 1.6 |
| Mg2+ | 750 | 97.0 ± 2.0 | 91.0 ± 1.2 | 98.0 ± 1.4 | 97.0 ± 1.8 | 96.0 ± 2.0 | 93.0 ± 1.7 |
| Ca2+ | 750 | 97.0 ± 1.2 | 90.0 ± 1.8 | 97.0 ± 1.5 | 97.0 ± 1.5 | 97.0 ± 2.0 | 93.0 ± 2.0 |
| I− | 750 | 98.0 ± 1.7 | 92.0 ± 2.0 | 99.0 ± 2.0 | 97.0 ± 1.7 | 97.0 ± 1.9 | 92.0 ± 2.1 |
| HCO3− | 500 | 98.0 ± 1.0 | 92.0 ± 1.2 | 98.0 ± 2.0 | 96.0 ± 2.0 | 98.0 ± 2.2 | 92.0 ± 2.0 |
| Zn2+ | 500 | 96.0 ± 1.2 | 91.0 ± 1.7 | 98.0 ± 1.8 | 95.0 ± 2.0 | 98.0 ± 2.2 | 92.0 ± 2.0 |
| Mn2+ | 500 | 96.0 ± 1.3 | 92.0 ± 1.7 | 99.0 ± 1.3 | 95.0 ± 1.2 | 98.0 ± 2.0 | 93.0 ± 2.0 |
3.6. Analytical features of SPE
Under the optimal conditions, the calibration curves were constructed for the determination of the Cr(II), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) ions concentrations, according to the mentioned procedure. Linearity was within the range of 20–600 μg L−1 for the Cr(III) ion, 5–700 μg L−1 for the Cu(II) ion, 20–700 μg L−1 for the Pb(II) ion, 10–600 μg L−1 for the Ni(II) ion, 5–600 μg L−1 for the Cd(II) ion, and 10–700 μg L−1 for the Co(II) ion. The determination correlation (R2) value was 0.999 for all the metal ions under study. The limit of detection (LOD) is defined as LOD = 3Sb/m, where Sb is the standard deviation of 8 replicates of the blank signals, and m is the slope of the calibration curve. For a sample volume of 50 mL, LODs were found to be 4.7, 3, 4, 1.7, 1.6, and 2.3 μg L−1 for the Cr(III), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) metal ions, respectively. The precision of this preconcentration method for a standard solution containing 0.2 mg L−1 of each metal ion (n = 4) was evaluated as the relative standard deviation (RSD%); they were found to be 2.1, 1.53, 2.58, 2.1, 2.62, and 2.09%, for the Cr(II), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) ions, respectively. In other words, the proposed extraction method can be considered as an efficient SPE in the determination of these metal ions.3.7. Determination of metal ions in various real samples
The applicability of the proposed adsorbent for the preconcentration of these metal ions in various real samples was investigated, which the results are presented in Table 7. The metal ion recovery percentages for various real samples were almost quantitative. Also, low and reasonable RSDs indicate the high capability of SPE using the activated carbon modified with the AgOH nanoparticles and the chelating agent in the simultaneous extraction of these metal ions in complex matrices.| Sample | Metal ion | Found (μg L−1), without spiking | Found (μg L−1), after spiking (100 μg L−1) | Recovery (%) |
|---|---|---|---|---|
| a Adsorption conditions: 0.12 g of adsorbent, 0.03 g of ligand, 1.38 mL min−1 of solution flow rate, pH = 5.73 and 200 mL of the sample with concentration of 0.2 mg L−1 of Cr(III), Cu(II), Pb(II), Ni(II), Cd(II), and Co(II) ions. Desorption conditions: 5.98 mL of HNO3 with the concentration of 4.98 mol L−1 and elution flow rate of 0.90 mL min−1 (numbers in parenthesis are the standard deviation for three replicate measurements). | ||||
| Tap water | Cr(III) | — | 98.39 (±1.38) | 98.39 |
| Cu(II) | 6.11 (±0.15) | 101.1 (±2.32) | 94.99 | |
| Pb(II) | — | 92.14 (±2.26) | 92.14 | |
| Ni(II) | — | 98.32 (±2.33) | 98.32 | |
| Cd(II) | — | 97.37 (±2.10) | 97.37 | |
| Co(II) | — | 95.63 (±2.76) | 95.63 | |
| Well water | Cr(III) | — | 98.96 (±2.47) | 98.96 |
| Cu(II) | 120.22 (±3.48) | 228.32 (±3.29) | 108.10 | |
| Pb(II) | 22.54 (±0.49) | 125.59 (±3.10) | 103.05 | |
| Ni(II) | 19.23 (±0.63) | 119.54 (±2.78) | 100.31 | |
| Cd(II) | 11.81 (±0.33) | 114.64 (±2.65) | 102.83 | |
| Co(II) | 32.40 (±0.49) | 136.86 (±3.54) | 104.46 | |
| Green tea | Cr(III) | — | 92.37 (±2.47) | 92.37 |
| Cu(II) | 93.08 (±2.69) | 201.33 (±5.13) | 108.25 | |
| Pb(II) | — | 97.74 (±3.34) | 97.74 | |
| Ni(II) | — | 98.57 (±2.67) | 98.57 | |
| Cd(II) | — | 101.09 (±2.38) | 101.09 | |
| Co(II) | 20.67 (±0.64) | 120.53 (±2.69) | 99.86 | |
| Meat (cow) | Cr(III) | — | 96.05 (±2.27) | 96.05 |
| Cu(II) | 12.04 (±0.37) | 106.66 (±3.34) | 94.62 | |
| Pb(II) | — | 91.04 (±2.63) | 91.04 | |
| Ni(II) | — | 94.36 (±1.94) | 94.36 | |
| Cd(II) | — | 93.24 (±2.52) | 93.24 | |
| Co(II) | 20.28 (±0.52) | 118.91 (±2.64) | 98.63 | |
| Fruit (peach) | Cr(III) | — | 95.01 (±3.02) | 95.01 |
| Cu(II) | 80.48 (±2.30) | 183.46 (±4.28) | 102.98 | |
| Pb(II) | — | 90.27 (±2.81) | 90.27 | |
| Ni(II) | 19.63 (±0.54) | 118.83 (±2.57) | 99.20 | |
| Cd(II) | — | 92.18 (±2.81) | 92.18 | |
| Co(II) | 20.17 (±0.49) | 119.62 (±2.82) | 99.45 | |
3.8. Comparison with literature
Comparison of the proposed extraction method with other SPE techniques using some modified activated carbons in the determination of several potentially toxic metal ions is given in Table 8. SPE method using the activated carbon modified with the silver hydroxide nanoparticles and the chelating agent has higher enrichment factors and recoveries of the metal ions compared with those indicated in the literature. Also, the LODs and linear dynamic ranges for the proposed extraction method are comparable with those reported in some previous works.| Metal ions | Adsorbent | Detection | LDRa | LODb | % RSDc | Elution conditions | EFd | Break through volume (mL) | % ERe | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| a Linear dynamic range (ng mL−1).b Limit of detection (S/N = 3), (ng mL−1).c Relative standard deviation.d Enrichment factor.e Extraction recovery.f Inductively coupled plasma mass spectrometry.g Flame atomic absorption spectrometry. | ||||||||||
| Cr(III) | Ethylenediamine-modified activated carbon (AC-EDA) | fICP-OES | — | 0.28 | 4.0 | 3.0 mL of 2% (%w/w) thiourea and 0.5 mol L−1 HCl solution with flow rate of 4.0 mL min−1 | 133.3 | 400 | >95 | 46 |
| 3.4 | ||||||||||
| Fe(III) | — | 0.22 | 1.6 | |||||||
| Hg(II) | — | 0.09 | 3.9 | |||||||
| Pb(II) | — | 0.17 | 2.1 | |||||||
| Cr(III) | Oxidized activated carbon modified with triethylenetetramine | ICP-OES | — | 0.71 | 3.7 | 0.5 mol L−1 HCl solution with the flow rate of 2.0 mL min−1 | — | 150 | >95 | 47 |
| Fe(III) | — | 0.35 | 2.2 | |||||||
| Pb(II) | — | 0.45 | 2.5 | |||||||
| Cr(III) | 1-(2-Formamidoethyl)-3-phenylurea functionalized activated carbon | ICP-OES | — | 0.15 | 3.2 | 2.0 mL of 2.0 mol L−1 HCl solution with the flow rate of 2.0 mL min−1 | 100 | 200 | >95 | 48 |
| Cu(II) | — | 0.41 | 2.5 | |||||||
| Fe(III) | — | 0.27 | 3.6 | |||||||
| Pb(II) | — | 0.36 | 1.9 | |||||||
| Pb(II) | 1-(2-pyridylazo)-2-naphthol impregnated activated carbon cloth | gFAAS | — | 0.1–2.8 | Low 6.3 | 10.0 mL of 3 mol L−1 HNO3 solution with the flow rate of 4.0 mL min−1 | 100 | 1000 | >95 | 49 |
| Cd(II) | — | |||||||||
| Ni(II) | — | |||||||||
| Cu(II) | Modified activated carbon with 1-acylthiosemicarbazide | ICP-OES | 1.85–100 with the R2 better than 0.999 | 0.20 | 4 | 3.0 mL of 2% CS(NH2)2 and 2.0 mol L−1 HCl solution with the flow rate of 3.0 mL min−1 | 100 | 300 | >95 | 50 |
| 3.5 | ||||||||||
| Hg(II) | 0.12 | 1.9 | ||||||||
| Pb(II) | 0.45 | 3.7 | ||||||||
| Cr(III) | Zincon-modified activated carbon | ICP-OES | — | 0.91 | 3.5 | 1 mL of 0.1 mol L−1 HCl solution with the flow rate of 4.0 mL min−1 | 150 | 150 | >95% | 51 |
| Pb(II) | 0.65 | 2.9 | ||||||||
| Pb(II) | 4-(2-Thiazolylazo) resorcinol-modified activated carbon | FAAS | — | 2.03 | 3.2 | 7.0 mL of 3 mol L−1 HNO3 solution with the flow rate of 3.0 mL min−1 | 143 | 1000 | >95% | 52 |
| Cd(II) | 0.15 | 2.7 | ||||||||
| Cu(II) | 0.19 | 4.6 | ||||||||
| Cu(II) | Silver nanoparticles loaded on activated carbon | FAAS | 20–200 | 4.9 | 4.1 | 10.0 mL of 4.0 mol L−1 HNO3 solution | 93.75 | 750 | >96% | 53 |
| Pb(II) | 30–200 | 3.9 | 3.9 | |||||||
| Zn(II) | 20–300 | 3.3 | 2.8 | |||||||
| Al(III) | Polyacrylonitrile activated carbon fibres | ICP-OES | 4–2000 | 1.1 | 3.1 | 3.0 mL of 1.5 mol L−1 HNO3 solution with the flow rate of 1.5 mL min−1 | 67 | 250 | >95% | 54 |
| Be(II) | 0.2–2000 | 0.06 | 2.5 | 50 | 150 | |||||
| Bi(III) | 0.44–2000 | 1.5 | 1.5 | 67 | 250 | |||||
| Cr(III) | 0.43–2000 | 0.13 | 2.5 | 83 | 250 | |||||
| Cu(II) | 0.77–2000 | 0.23 | 2.1 | 83 | 250 | |||||
| Fe(III) | 0.37–2000 | 0.11 | 1.7 | 83 | 250 | |||||
| Pb(II) | 2.1–2000 | 0.63 | 3.5 | 50 | 150 | |||||
| Cr(III) | Activated carbon modified with silver hydroxide nanoparticles and ligand | FAAS | 20–600 | 4.7 | 2.1 | 5.98 mL of 4.98 mol L−1 HNO3 solution with the flow rate of 0.9 mL min−1 | 167.2 | 1000 | >98 | This work |
| Cu(II) | 5–700 | 3 | 1.53 | 167.2 | 1000 | |||||
| Pb(II) | 20–700 | 4 | 2.58 | 167.2 | 1000 | |||||
| Ni(II) | 10–600 | 1.7 | 2.1 | 83.6 | 1000 | |||||
| Cd(II) | 5–600 | 1.6 | 2.62 | 167.2 | 750 | |||||
| Co(II) | 10–700 | 2.3 | 2.09 | 125.4 | 500 | |||||
4. Conclusion
A simple, fast, reproducible, and selective solid-phase extraction (SPE) procedure was developed using a new, economic, effective, and eco-friendly adsorbent, the activated carbon modified with the silver hydroxide nanoparticles and chelating agent, for determining the chromium, copper, lead, nickel, cadmium, and cobalt metal ions. Acid treatment of the carbon obtained from eucalyptus wood caused to improve its linkage with the nanomaterials and chelating agent. The use of the response surface methodology for an efficient optimization of the SPE process was another valuable advantage of this work, so that, without any reduction in efficiency, CCD lowered the analysis time and experimental expense. Moreover, the low LODs and high enrichment factors indicate the high capability of SPE using an efficient adsorbent in the determination of trace amounts of the potentially toxic metal ions at μg L−1 levels in high volumes.Acknowledgements
The authors would like to thank the Semnan University Research Council for the financial support of this work. The authors also express the special thanks to Dr Alireza Asghari (Department of Chemistry, Semnan University, Semnan, Iran) due to his support in this project.References
- J. N. Bianchin, E. Martendal, R. Mior, V. N. Alves, C. S. T. Araújo, N. M. M. Coelho and E. Carasek, Talanta, 2009, 78, 333–336 CrossRef CAS PubMed.
- J. Sorbie, D. Olatunbosun, W. E. Corbett and L. S. Valberg, Can. Med. Assoc. J., 1971, 104, 777 CAS.
- J. Kristiansen, J. M. Christensen, T. Henriksen, N. H. Nielsen and T. Menné, Anal. Chim. Acta, 2000, 403, 265–272 CrossRef CAS.
- S. A. Katz and H. Salem, J. Appl. Toxicol., 1993, 13, 217–224 CrossRef CAS PubMed.
- Y.-H. Sung and S.-D. Huang, Anal. Chim. Acta, 2003, 495, 165–176 CrossRef CAS PubMed.
- J. Yin, Z. Jiang, G. Chang and B. Hu, Anal. Chim. Acta, 2005, 540, 333–339 CrossRef CAS PubMed.
- E. L. Silva, P. dos Santos Roldan and M. F. Gine, J. Hazard. Mater., 2009, 171, 1133–1138 CrossRef CAS PubMed.
- M. Soylak and N. D. Erdogan, J. Hazard. Mater., 2006, 137, 1035–1041 CrossRef CAS PubMed.
- P. K. Srungaram, K. K. Ayyalasomayajula, F. Yu-Yueh and J. P. Singh, Spectrochim. Acta, Part B, 2013, 87, 108–113 CrossRef CAS PubMed.
- M. Soylak, S. Saracoglu and L. Elci, Trace Elem. Electrolytes, 2001, 18, 129–133 Search PubMed.
- M. Tuzen, K. O. Saygi and M. Soylak, J. Hazard. Mater., 2008, 152, 632–639 CrossRef CAS PubMed.
- M. Soylak, A. U. Karatepe, L. Elçİ and M. Doğan, Turk. J. Chem., 2003, 27, 235–242 CAS.
- S. Akman, M. Ozcan and E. Demirel, J. Anal. At. Spectrom., 2002, 17, 743–745 RSC.
- M. Soylak, M. Elci and M. Dogan, Fresenius Environ. Bull., 1996, 5, 148–155 CAS.
- H. K. Chae, D. Y. Siberio-Pérez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523–527 CrossRef CAS PubMed.
- X. Wang, X. Liang, Y. Wang, X. Wang, M. Liu, D. Yin, S. Xia, J. Zhao and Y. Zhang, Desalination, 2011, 278, 231–237 CrossRef CAS PubMed.
- R. H. Hesas, W. M. A. W. Daud, J. N. Sahu and A. Arami-Niya, J. Anal. Appl. Pyrolysis, 2013, 100, 1–11 CrossRef PubMed.
- A. Bhatnagar, W. Hogland, M. Marques and M. Sillanpää, Chem. Eng. J., 2013, 219, 499–511 CrossRef CAS PubMed.
- H. ShamsiJazeyi and T. Kaghazchi, J. Ind. Eng. Chem., 2010, 16, 852–858 CrossRef CAS PubMed.
- N. Soudani, S. Souissi-najar and A. Ouederni, Chin. J. Chem. Eng., 2013, 21, 1425–1430 CrossRef.
- M. Ghaedi, M. Ghayedi, S. N. Kokhdan, R. Sahraei and A. Daneshfar, J. Ind. Eng. Chem., 2013, 19, 1209–1217 CrossRef CAS PubMed.
- M. Ghaedi, F. Ahmadi and A. Shokrollahi, J. Hazard. Mater., 2007, 142, 272–278 CrossRef CAS PubMed.
- M. Ghaedi, J. Tashkhourian, M. Montazerozohori and M. Soylak, Int. J. Environ. Anal. Chem., 2011, 93, 386–400 CrossRef PubMed.
- B. Barfi, M. Rajabi, M. Zadeh, M. Ghaedi, M. Salavati-Niasari and R. Sahraei, Microchim. Acta, 2015, 182, 1187–1196 CrossRef CAS.
- A. Asghari, H. Farzinia, M. Rajabi and M. Ghaedi, Desalin. Water Treat., 2013, 52, 5430–5441 CrossRef PubMed.
- M. Ghaedi, E. A. barakat, A. Asfaram, B. Mirtamizdoust, A. A. Bazrafshan and S. Hajati, RSC Adv., 2015, 5, 42376–42387 RSC.
- P. Vanloot, J. L. Boudenne, L. Vassalo, M. Sergent and B. Coulomb, Talanta, 2007, 73, 237–245 CrossRef CAS PubMed.
- F. L. Melquiades, P. S. Parreira, M. J. Yabe, M. Z. Corazza, R. Funfas and C. R. Appoloni, Talanta, 2007, 73, 121–126 CrossRef CAS PubMed.
- I. H. Lee, Y.-C. Kuan and J.-M. Chern, J. Hazard. Mater., 2006, 138, 549–559 CrossRef CAS PubMed.
- L. A. Escudero, S. Cerutti, R. A. Olsina, J. A. Salonia and J. A. Gasquez, J. Hazard. Mater., 2010, 183, 218–223 CrossRef CAS PubMed.
- T. N. Decaestecker, W. E. Lambert, C. H. van Peteghem, D. Deforce and J. F. van Bocxlaer, J. Chromatogr. A, 2004, 1056, 57–65 CrossRef CAS PubMed.
- L. Živanović, A. Ličanski, M. Zečević, B. Jocić and M. Kostić, J. Pharm. Biomed. Anal., 2008, 47, 575–585 CrossRef PubMed.
- M. Sarkar and P. Majumdar, Chem. Eng. J., 2011, 175, 376–387 CrossRef CAS PubMed.
- K. Yetilmezsoy, S. Demirel and R. J. Vanderbei, J. Hazard. Mater., 2009, 171, 551–562 CrossRef CAS PubMed.
- B. Barfi, A. Asghari, M. Rajabi, S. Sabzalian, F. Khanalipoor and M. Behzad, RSC Adv., 2015, 5, 31930–31941 RSC.
- T. Lundstedt, E. Seifert, L. Abramo, B. Thelin, Å. Nyström, J. Pettersen and R. Bergman, Chemom. Intell. Lab. Syst., 1998, 42, 3–40 CrossRef CAS.
- C. Stalikas, Y. Fiamegos, V. Sakkas and T. Albanis, J. Chromatogr. A, 2009, 1216, 175–189 CrossRef CAS PubMed.
- Ş. Tokalıoğlu and F. Gürbüz, Food Chem., 2010, 123, 183–187 CrossRef PubMed.
- M. Ghaedi, A. Shokrollahi, A. H. Kianfar, A. S. Mirsadeghi, A. Pourfarokhi and M. Soylak, J. Hazard. Mater., 2008, 154, 128–134 CrossRef CAS PubMed.
- M. Ghaedi, Z. Rozkhoosh, A. Asfaram, B. Mirtamizdoust, Z. Mahmoudi and A. A. Bazrafshan, Spectrochim. Acta, Part A, 2015, 138, 176–186 CrossRef CAS PubMed.
- S. Park, V. Mathur and R. P. Planalp, Polyhedron, 1998, 17, 325–330 CrossRef CAS.
- R. H. Myers, D. C. Montgomery and C. M. Anderson-Cook, Response surface methodology: process and product optimization using designed experiments, John Wiley & Sons, 2009 Search PubMed.
- M. K. Amini, M. Ghaedi, A. Rafi, I. Mohamadpoor-Baltork and K. Niknam, Sens. Actuators, B, 2003, 96, 669–676 CrossRef CAS PubMed.
- M. A. Ahmad and R. Alrozi, Chem. Eng. J., 2010, 165, 883–890 CrossRef CAS PubMed.
- C. Cojocaru and G. Zakrzewska-Trznadel, J. Membr. Sci., 2007, 298, 56–70 CrossRef CAS PubMed.
- Z. Li, X. Chang, X. Zou, X. Zhu, R. Nie, Z. Hu and R. Li, Anal. Chim. Acta, 2009, 632, 272–277 CrossRef CAS PubMed.
- L. Zhang, X. Chang, Z. Li and Q. He, J. Mol. Struct., 2010, 964, 58–62 CrossRef CAS PubMed.
- Z. Tu, Q. He, X. Chang, Z. Hu, R. Gao, L. Zhang and Z. Li, Anal. Chim. Acta, 2009, 649, 252–257 CrossRef CAS PubMed.
- Z. A. Alothman, E. Yilmaz, M. Habila and M. Soylak, Ecotoxicol. Environ. Saf., 2015, 112, 74–79 CrossRef CAS PubMed.
- R. Gao, Z. Hu, X. Chang, Q. He, L. Zhang, Z. Tu and J. Shi, J. Hazard. Mater., 2009, 172, 324–329 CrossRef CAS PubMed.
- Z. Li, X. Chang, Z. Hu, X. Huang, X. Zou, Q. Wu and R. Nie, J. Hazard. Mater., 2009, 166, 133–137 CrossRef CAS PubMed.
- M. Habila, E. Yilmaz, Z. A. Alothman and M. Soylak, J. Ind. Eng. Chem., 2014, 20, 3989–3993 CrossRef CAS PubMed.
- M. Ghaedi, M. Montazerozohori, M. Sajedi, M. Roosta, M. Nickoosiar Jahromi and A. Asghari, J. Ind. Eng. Chem., 2013, 19, 1781–1787 CrossRef CAS PubMed.
- X. L. L. Zhang, W. Xia, Y. Zhang and W. Zhang, Int. J. Environ. Anal. Chem., 2014, 94, 728–741 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra14005f |
| This journal is © The Royal Society of Chemistry 2015 |