Study of the electronic structure, stability and magnetic quenching of CrGen (n = 1–17) clusters: a density functional investigation†
Abstract
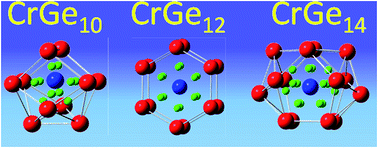
In the present report the evolution of the electronic structure, stability and magnetic quenching of CrGen nanoclusters has been carried out using density functional theory (DFT). From the nature of the variation of the different thermodynamic and chemical parameters, the CrGe10 and CrGe14 ground state clusters are identified as the most stable species. It is observed that the enhanced stability of CrGe10 and CrGe14 are due to the closed shell filled structure of the Cr-atomic orbitals and follow the 18-electron counting rule. It is found that the strong mixing of the Cr d-orbital with the s- and p-atomic orbitals of the Ge atoms in the cluster are mainly responsible for the stability and quenching of the Cr magnetic moment in the clusters. Calculated CPs also give additional information about the bonding and its effect on the stability of the clusters. Calculated IR and Raman spectra also support these results.

 Please wait while we load your content...
Please wait while we load your content...