Solute-induced perturbation of methanol–water association†
Abstract
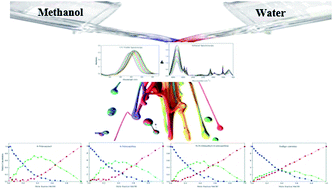
This article addresses experimental evidence of changes in the equilibrium constant of methanol–water association induced by solutes. The behavior of four solutes (solvatochromic dyes) in methanol–water binary mixtures is probed using augmentation of infrared and UV-Vis spectroscopy methods followed by multivariate analysis. In order to get more reliable concentration and spectral profiles, with fewer ambiguities, complementarity and coupling theorems have been utilized. A ternary system was resolved using multivariate analysis on the noted augmented data for each chemical probe. Resultant concentration profiles showed the unique behavior of each solute in the binary-solvent system. Therefore, an individual association constant for the formation of the methanol–water association was achieved for each solvatochromic probe. Indeed, different solutes can change the solvent–solvent interaction based on their hydrogen binding affinity. Diverse hydrogen binding affinities for different solutes were investigated using charge distribution analysis via molecular electrostatic potential (MEP) calculations as well as the atomic charge on the oxygen atoms. In addition, obtained spectral profiles of standard solvatochromic probes were used to calculate solvatochromic parameters of dipolarity/polarizability and hydrogen-bonding basicity of three resolved components (i.e. methanol, water and methanol–water complex surrounded probes).

 Please wait while we load your content...
Please wait while we load your content...