Antioxidant properties can be tuned in the presence of an external electric field: accurate computation of O–H BDE with range-separated density functionals†
Manash Protim Borpuzari,
Rakiba Rohman and
Rahul Kar*
Department of Chemistry, Dibrugarh University, Dibrugarh, Assam, India-786004. E-mail: rahul.kar.dib@gmail.com
First published on 8th September 2015
Abstract
In this article, we have studied the effect of the external electric field on the antioxidant properties of gallic and caffeic acids. The variation of the O–H bond dissociation enthalpy (BDE), adiabatic ionization energy, proton dissociation enthalpy, proton affinity and electron transfer enthalpy, in the presence of an external electric field is studied. It is found that the antioxidant properties can be tuned by the application of an external electric field. In addition, the O–H bond strength, qualitatively measured from the O–H bond length, is found to depend on the external electric field. Furthermore, the performance of seven range-separated density functionals in the presence of the external electric field is reported for the first time. On comparing with the composite model CBS-QB3, it is found that the LC-BLYP functional reproduces the O–H BDE with high accuracy.
Introduction
Antioxidants have a great potential to act as therapeutic agents against a wide range of ailments including neurodegenerative diseases, cancer, diabetes, cardiovascular dysfunctions, inflammatory diseases, ageing, etc.1–5 These ailments have attracted the research community, over a few decades, to increase the efficiency of natural antioxidants. Due to regular metabolic routes and some external factors, free radicals, classified as reactive oxygen species (ROS), reactive nitrogen species (RNS) and reactive sulfur species (RSS), are produced in the human body which can start chain reaction in cells and cause damage or death to the cells. Antioxidants terminate these chain reactions by removing the free radicals and are defined as the substances that delay, prevent or remove oxidative damage to a target molecule.6 However, reactive oxygen species sometimes play a positive role depending on the classification of oxidative stress.7The human antioxidant system is divided into two major groups namely, enzymatic and non-enzymatic antioxidants. Some of the enzymatic antioxidants are glutathione peroxidase, catalase, superoxide dismutase, etc. On the other hand, some endogenous non-enzymatic antioxidants are vitamins (A), enzyme cofactors (Q10), nitrogen compounds (uric acid), and peptides (glutathione).8 Apart from these endogenous antioxidants, human health is dependent on various other antioxidants that are in the diet to maintain the free radical concentration at low level. Recent study reveals that most of the dietary antioxidants can behave as prooxidants (chemicals that include oxidative stress, usually through the formation of reactive species or by inhibiting antioxidant systems) depending on their concentration and nature of neighboring molecules.8,9
Among the phytochemicals, polyphenols got tremendous attention due to the recognition of its antioxidant properties10–12 and its great abundance in our diet.13–15 On their structural basis, they are categorized as phenolic acids, flavonoids, stilbenes, lignans, tocopherols, etc. The flavonoid group is further divided into six classes of compounds namely, flavonols, flavones, isoflavones, flavanones, anthocyanidins, and flavanols. Natural phenolics are also classified as lipophilic group (tocopherols mainly) and hydrophilic group (phenolic acids and flavonoids) on the basis of their solubility.16 Now-a-days, some hybrid systems are synthesized and their antioxidant properties are confirmed by density functional theory (DFT).17
The antioxidant properties of polyphenols are attributed to the presence of hydroxyl groups in its structure that scavenge free radicals via (i) hydrogen atom transfer (HAT), (ii) single electron transfer followed by proton transfer (SET-PT), and (iii) sequential proton loss electron transfer (SPLET). Thus, their corresponding properties such as O–H bond dissociation enthalpy (BDE), adiabatic ionization energy (IE), proton dissociation enthalpy (PDE), proton affinity (PA), and electron transfer enthalpy (ETE) are of prime importance. Many theoretical as well as experimental studies revealed that depending on the structure–antioxidant activity relationship and some other external factors (such as solvent effect), phenolic antioxidants work through any of these mechanisms.18–22
Our aim in this article is to understand the behavior of the antioxidants in the presence of an external perturbation in the form of the external electric field. Earlier, the effect of electric field on hydrogen bond network of methanol and on structures and energetic of water clusters has been investigated.23,24 Influence of the electric field on the chemical reactivity descriptors has been extensively studied for a variety of molecular systems.25–28 Recently, the influence of external electric field on the stability and reactivity of DNA bases and base pairs were studied.29,30 Very recently, in an experimental report, the effect of pulsed electric field on the antioxidant activity of glutathione was studied.31 This motivated us to theoretically understand the behavior of antioxidant molecules in the presence of an external electric field. We anticipate that the behavior of antioxidants can be tuned by the application of such field, and hence would contribute to explore new insights on such class of molecules.
One of the important properties of this class of molecules is the BDE of the O–H bond. However, it is found in the literature that most of the density functionals, such as B3LYP, significantly underestimate X–H (X = C, N, O, Si, P, S) BDE by as much as 3–6 kcal mol−1.32 Moreover, Gilbert has tested the performance of various density functionals in the prediction of structure and BDE of amine–borane complex.33 He has found that the performance of B3LYP is poor in predicting structure and BDE of such amine–borane complex. Furthermore, in the predictions of C–SO2R BDE, the performance of M06-2X is found to be the best among the 13 tested density functionals.34 They have found that root mean square deviation (RMSD) of M06-2X is 1.6 kcal mol−1 whereas, RMSD of B3LYP is 9.4 kcal mol−1. Recently, Chan et al. have developed a comprehensive set of high-level theoretical bond dissociation enthalpies (BDE261) by calculating BDE of 261 molecules at high level W1w composite method and found that the mean absolute deviation (MAD) of B3LYP and B98 are 26.7 kJ mol−1 and 15.0 kJ mol−1, respectively.35 More importantly, CAM-B3LYP and ωB97X, which are range-separated version of B3LYP and B98, produce lower MAD than B3LYP and B98, respectively (18.9 kJ mol−1 and 8.4 kJ mol−1, respectively). Range-separated functionals are new type of functionals which are developed to overcome the drawbacks of conventional density functionals.36–38 In these functionals, by using error function and a range-separation parameter (μ), the coulomb operator i.e. r12−1 is spilt into long-range interaction term (first term in eqn (1)) and short-range interaction term (second term in eqn (1)). The short-range interaction term is evaluated by DFT exchange functional whereas long-range term is evaluated by Hartree–Fock (HF) exchange integral.39,40
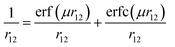 | (1) |
The range-separated functionals are found to be useful in reproducing nonlinear optical properties, orbital energies, Rydberg excitations, charge transfer excitations, and van der Waals energy.41–48 Moreover, these functionals reproduce reaction barrier heights and reaction enthalpies quite accurately.49 To the best of our knowledge, the performance of the range-separated functionals in the presence of the external electric field has not been studied and is unavailable in the literature. Therefore, it would be interesting to evaluate the performance of the range-separated density functional in computing the O–H BDE in presence of an external electric field.
In this article, firstly, we carried out a systematic theoretical study to understand the behavior of the properties such as BDE, IE, PDE, PA and ETE in the presence of the external electric field. Thus, our study is expected to throw light on the efficiency of the antioxidants in the presence of such fields. Secondly, we would like to quantitatively evaluate the performance of density functional in reproducing the O–H BDE in the presence of the external electric field. The present article is arranged as follows: next section provides the Computational details. Then, we present the results and discussion and finally, the conclusions are presented.
Computational details
To understand the behavior of the antioxidants in the presence of the external electric field, firstly, the geometries of all the antioxidant molecules, including radicals, radical cations, and anions, have been fully optimized in LC-BLYP41/6-311++G(3df,2p) level of theory at each electric field value (i.e., −0.010, −0.008, −0.006, −0.004, −0.002, 0.000, 0.002, 0.004, 0.006, 0.008, 0.010 a.u.) in x, y and z-directions [1 a.u. of electric field = 51.4 V Å−1]. Harmonic vibrational frequency calculations have been performed at the same level of theory to confirm that all the optimized structures are minima. Unrestricted calculations have been performed for the open-shell systems, such as radicals and radical cation species and no spin contamination is found. The molecular enthalpy (H) at 298.15 K is consisted of sum of electronic and thermal enthalpies (in which the vibrational contributions include zero-point vibrational energy) calculated at LC-BLYP/6-311++G(3df,2p) level of theory. The gas phase enthalpy of the proton and electron are 0.002363 and 0.001198 Hartree, respectively, taken from ref. 50. Secondly, for the quantitative evaluation of the density functionals in predicting the BDE of the antioxidants in the presence of external electric field, we have fully optimized the molecules and radicals using 6-311++G(3df,2p) basis set at each field value (i.e., −0.010, −0.008, −0.006, −0.004, −0.002, 0.000, 0.002, 0.004, 0.006, 0.008, 0.010 a.u.) considering the following range-separated functionals for our study: LC-BLYP,41 LC-ωPBE,51 ωB97,52 ωB97X,52 ωB97XD,53 M11,54 and CAM-B3LYP.55 For comparison, we have also calculated the BDE with B3LYP and M06-2X56 density functionals. As our reference, we have performed the composite method CBS-QB3 calculations. All the computations have been performed using the Gaussian 09 software.57 The optimized geometries of all the species can be found in the ESI.†Results and discussion
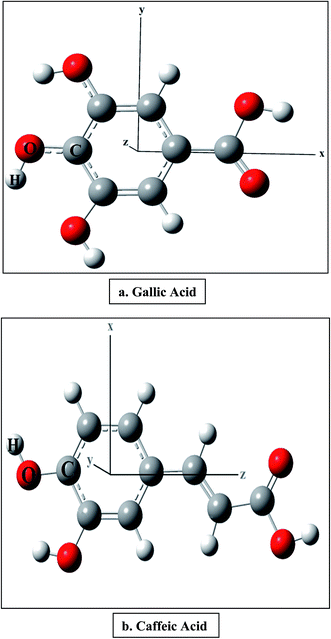
We have considered two polyphenolic molecules, i.e., gallic and caffeic acids, due to their recognition as natural antioxidants, and calculated reaction enthalpies viz., BDE, PDE, PA, ETE and IE in the presence of varying external electric field. We try to explain our results, based on the x-, y-, and z-directions (Fig. 1). However, from a chemists point of view, the three Cartesian axes may be modelled as follows: when the external electric field is applied (i) along (i.e., towards and opposite to) the C–O bond of the most stable phenoxyl radical, produced after the abstraction of H atom; (ii) perpendicular to the C–O bond of the most stable phenoxyl radical, and in the plane of the ring; (iii) perpendicular to the molecular plane. Firstly, the behavior of the antioxidant is discussed when the field is applied along the C–O bond and then we shall discuss their behavior in other two directions. Later, we shall discuss the effect of the electric field on the bond length of the O–H bond of gallic and caffeic acids, and finally, we shall discuss the performance of range-separated density functionals in producing the BDE in the presence of electric field.Electric field applied along the C–O bond
The optimized structures of gallic and caffeic acids at zero field are shown with the Cartesian axes in Fig. 1. It has been reported that out of the three OH groups in gallic acid, 4-OH is the stabilized radical. Similarly, in case of caffeic acid, the formation of two radicals is possible, 3-OH and 4-OH, and it has been earlier reported that the electronic delocalization effect is responsible for the energetic stability of the 4-OH radical.18 The BDE is calculated from the molecular enthalpy (H) of the species involved as follows:| BDE = H(ArO˙) + H(H˙) − H (ArOH) | (2) |
When the external electric field is applied towards the C–O bond (i.e., along the negative x-axis; Fig. 1) the O–H BDE linearly decrease on increasing the field for both gallic and caffeic acid (Table 1 and Fig. 2). For instance, the BDE value for gallic acid, in absence of an external electric field, is computed to be 81.869 kcal mol−1. On gradually increasing the electric field to 0.010 a.u. (towards the C–O bond), this value decreases to 72.446 kcal mol−1. Similarly, for caffeic acid the BDE value decreases from 77.007 kcal mol−1 to 63.651 kcal mol−1 on increasing the external electric field applied towards the C–O bond (i.e., along the negative z-axis; Fig. 1). On the other hand, the BDE value increases on increasing the external electric field in the opposite direction to the C–O bond for these molecular systems (Table 1 and Fig. 2). For gallic acid, when the field is applied opposite to the C–O bond (i.e., along positive x-axis; Fig. 1), BDE increases to 91.003 kcal mol−1, and for caffeic acid (when the field is applied towards the positive z-axis; Fig. 1), it increases to 89.030 kcal mol−1 (Table 1). It is known that BDE is a measure of the ability of an antioxidant to transfer a hydrogen atom to a free radical. Thus, the antioxidant would be more efficient when BDE value comparatively decreases. Hence, we understand that the antioxidant behavior of gallic and caffeic acids would be increased when the electric field is applied towards the C–O bond (of most stable phenoxyl radical produced after the abstraction of H atom).
| Electric field | Along the C–O bond | Perpendicular to molecular plane | Perpendicular to the C–O bond | |||
|---|---|---|---|---|---|---|
| GA | CA | GA | CA | GA | CA | |
| 0.010 | 91.003 | 89.030 | 83.111 | 78.953 | 84.696 | 73.118 |
| 0.008 | 89.195 | 86.671 | 82.708 | 78.249 | 84.197 | 73.894 |
| 0.006 | 87.381 | 84.297 | 82.357 | 77.664 | 83.662 | 74.679 |
| 0.004 | 85.560 | 81.900 | 82.104 | 77.226 | 83.098 | 75.461 |
| 0.002 | 83.708 | 79.473 | 81.936 | 76.983 | 82.499 | 76.236 |
| 0.000 | 81.869 | 77.007 | 81.869 | 77.007 | 81.869 | 77.007 |
| −0.002 | 80.018 | 74.491 | 81.947 | 77.223 | 81.232 | 77.772 |
| −0.004 | 78.151 | 71.913 | 82.125 | 77.701 | 80.543 | 78.530 |
| −0.006 | 76.269 | 69.258 | 82.389 | 78.339 | 79.824 | 79.284 |
| −0.008 | 74.368 | 66.507 | 82.750 | 79.123 | 79.077 | 80.034 |
| −0.010 | 72.446 | 63.651 | 83.134 | 79.992 | 78.301 | 80.780 |
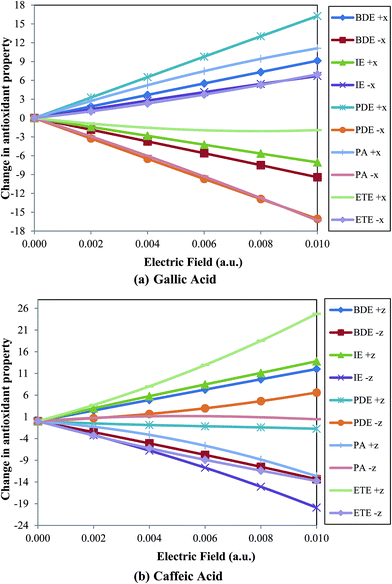 | ||
| Fig. 2 Variation of change in antioxidant property (in kcal mol−1) with respect to zero field for (a) gallic acid and (b) caffeic acid with electric field (in a.u.). | ||
The IE shows opposite behavior for gallic and caffeic acids. The values of the adiabatic ionization energy (IE), calculated using eqn (3), are presented in Table 2.
| IE = H(ArOH˙+) + H(e−) − H(ArOH) | (3) |
| Electric field | Along the C–O bond | Perpendicular to molecular plane | Perpendicular to the C–O bond | |||
|---|---|---|---|---|---|---|
| GA | CA | GA | CA | GA | CA | |
| 0.010 | 185.104 | 200.184 | 193.367 | 187.174 | 193.424 | 196.930 |
| 0.008 | 186.500 | 197.484 | 192.974 | 186.837 | 193.400 | 194.773 |
| 0.006 | 187.915 | 194.841 | 192.633 | 186.570 | 193.263 | 192.646 |
| 0.004 | 189.339 | 192.133 | 192.386 | 186.384 | 193.012 | 190.537 |
| 0.002 | 190.740 | 189.330 | 192.224 | 186.308 | 192.636 | 188.444 |
| 0.000 | 192.159 | 186.365 | 192.159 | 186.365 | 192.159 | 186.365 |
| −0.002 | 193.560 | 183.153 | 192.230 | 186.583 | 191.621 | 184.303 |
| −0.004 | 194.938 | 179.608 | 192.399 | 186.913 | 190.996 | 182.257 |
| −0.006 | 196.283 | 175.660 | 192.652 | 187.310 | 190.326 | 180.229 |
| −0.008 | 197.592 | 171.276 | 192.998 | 187.769 | 189.623 | 178.220 |
| −0.010 | 198.860 | 166.472 | 193.367 | 188.242 | 188.897 | 176.232 |
It can be observed that the IE value increases for gallic acid while decreases for caffeic acid on increasing the external electric field applied in the same direction of C–O bond (Fig. 2). For instance, IE for gallic and caffeic acids in absence of an electric field are 192.159 kcal mol−1 and 186.365 kcal mol−1, respectively. When the field is applied towards the C–O bond, in case of gallic acid, this value increases to 198.860 kcal mol−1, while for caffeic acid, it decreases to 166.472 kcal mol−1 at 0.010 a.u. electric field. However, on increasing the electric field in opposite direction to the C–O bond the IE value of gallic acid decreases to 185.104 kcal mol−1, while for caffeic acid, it increases to 200.184 kcal mol−1. An antioxidant with low IE value indicates a greater tendency to convert free radicals into anions enhancing the antioxidant activity. Thus, gallic acid can behave as a better antioxidant when an electric field is applied in a direction opposite to the C–O bond, while caffeic acid shows better antioxidant activity on applying electric field in the direction of C–O bond.
PDE is calculated from the difference between the sum of enthalpies of radical species and proton with the enthalpy of radical cation species as follows,
| PDE = H(ArO˙) + H(H+) − H(ArOH˙+) | (4) |
PDE of phenolic radical cation (ArOH+˙) should be lower so that the proton can be easily transferred to the anion (produced earlier by the transfer of one electron from the antioxidant) and the more stable phenoxyl radical (ArO˙) can be formed. In this study, we have observed that the PDE values (Table 3) show similar trend with BDE values for gallic acid and opposite trend for caffeic acid (Fig. 2). On increasing the electric field in the direction of the C–O bond from zero to 0.010 a.u. the PDE value for gallic acid is varied from 201.013 kcal mol−1 to 184.950 kcal mol−1, while in case of caffeic acid, the same is varied from 201.944 kcal mol−1 to 208.543 kcal mol−1. Thus, the PDE value decreases for gallic acid and increases for caffeic acid when electric field is applied in the direction of the C–O bond. Of course, the PDE values show opposite trend for both gallic and caffeic acid when electric field is increased in the opposite direction to the C–O bond. On increasing the field to 0.010 a.u. in the opposite direction, PDE for gallic acid increases to 217.263 kcal mol−1, while for caffeic acid, it decreases to 200.210 kcal mol−1.
| Electric field | Along the C–O bond | Perpendicular to molecular plane | Perpendicular to C–O bond | |||
|---|---|---|---|---|---|---|
| GA | CA | GA | CA | GA | CA | |
| 0.010 | 217.263 | 200.210 | 201.109 | 203.144 | 202.637 | 187.552 |
| 0.008 | 214.037 | 200.530 | 201.076 | 202.755 | 202.139 | 190.463 |
| 0.006 | 210.791 | 200.781 | 201.049 | 202.420 | 201.724 | 193.358 |
| 0.004 | 207.534 | 201.080 | 201.030 | 202.155 | 201.399 | 196.236 |
| 0.002 | 204.273 | 201.448 | 201.017 | 201.980 | 201.168 | 199.097 |
| 0.000 | 201.013 | 201.944 | 201.013 | 201.944 | 201.013 | 201.944 |
| −0.002 | 197.764 | 202.643 | 201.022 | 201.946 | 200.916 | 204.773 |
| −0.004 | 194.526 | 203.617 | 201.039 | 202.102 | 200.859 | 207.586 |
| −0.006 | 191.311 | 204.923 | 201.062 | 202.354 | 200.823 | 210.380 |
| −0.008 | 188.119 | 206.573 | 201.094 | 202.697 | 200.796 | 213.156 |
| −0.010 | 184.950 | 208.543 | 201.132 | 203.115 | 200.769 | 215.912 |
PA of ArO− anion of both gallic and caffeic acid shows same trend as that of the PDE values (Table 4 and Fig. 2). The PA is calculated from
| PA = H(ArO−) + H(H+) − H (ArOH) | (5) |
| Electric field (in a.u.) | Along the C–O bond | Perpendicular to molecular plane | Perpendicular to C–O bond | |||
|---|---|---|---|---|---|---|
| GA | CA | GA | CA | GA | CA | |
| 0.010 | 341.205 | 308.976 | 321.654 | 324.345 | 331.274 | 307.885 |
| 0.008 | 339.522 | 312.784 | 321.256 | 323.502 | 331.113 | 310.696 |
| 0.006 | 337.556 | 315.973 | 320.823 | 322.769 | 330.910 | 313.483 |
| 0.004 | 335.319 | 318.485 | 330.117 | 322.172 | 330.671 | 316.233 |
| 0.002 | 332.806 | 320.344 | 330.111 | 321.763 | 330.396 | 318.946 |
| 0.000 | 330.085 | 321.616 | 330.085 | 321.616 | 330.085 | 321.616 |
| −0.002 | 327.162 | 322.389 | 330.114 | 321.746 | 329.773 | 324.249 |
| −0.004 | 324.046 | 322.750 | 330.124 | 322.132 | 329.407 | 326.842 |
| −0.006 | 320.766 | 322.776 | 320.839 | 322.672 | 329.012 | 329.393 |
| −0.008 | 317.337 | 322.532 | 321.273 | 323.350 | 328.589 | 331.903 |
| −0.010 | 313.778 | 322.081 | 321.648 | 324.104 | 328.138 | 334.371 |
For ArO− anion of gallic acid, it decreases from 330.085 kcal mol−1 to 313.778 kcal mol−1, while for ArO− anion of caffeic acid, it increases from 321.616 kcal mol−1 to 322.081 kcal mol−1 when field is applied in the direction of the C–O bond. Similarly, it shows opposite behavior for the antioxidants when the electric field is applied in the direction opposite to the C–O bond (Fig. 2). It is found to be better to decrease the PA values of ArO− anion on applying electric field to enhance the transfer of a proton from the antioxidant to free radical.
ETE is calculated using the following equation:
| ETE = H(ArO˙) + H(e−) − H(ArO−) | (6) |
It can be observed that the ETE shows similar trend with IE for both gallic and caffeic acids (Fig. 2). In case of gallic acid, ETE increases from 63.087 kcal mol−1 to 70.032 kcal mol−1 on increasing the electric field in the direction of the C–O bond, while it decreases to 61.163 kcal mol−1 in the opposite direction (Table 5). On the contrary, for caffeic acid, ETE decreases from 66.693 kcal mol−1 to 52.934 kcal mol−1 with increase in the electric field in the direction of the C–O bond while, increases to 91.418 kcal mol−1 in the direction opposite to the C–O bond.
| Electric field (in a.u.) | Along the C–O bond | Perpendicular to molecular plane | Perpendicular to C–O bond | |||
|---|---|---|---|---|---|---|
| GA | CA | GA | CA | GA | CA | |
| 0.010 | 61.163 | 91.418 | 72.821 | 65.972 | 64.787 | 77.922 |
| 0.008 | 61.015 | 85.230 | 72.794 | 66.089 | 64.426 | 75.468 |
| 0.006 | 61.150 | 79.649 | 72.860 | 66.221 | 64.078 | 73.119 |
| 0.004 | 61.554 | 74.728 | 63.299 | 66.367 | 63.739 | 70.874 |
| 0.002 | 62.208 | 70.434 | 63.130 | 66.525 | 63.408 | 68.732 |
| 0.000 | 63.087 | 66.693 | 63.087 | 66.693 | 63.087 | 66.693 |
| −0.002 | 64.161 | 63.407 | 63.138 | 66.783 | 62.764 | 64.667 |
| −0.004 | 65.418 | 60.476 | 63.315 | 66.882 | 62.449 | 62.738 |
| −0.006 | 66.829 | 57.807 | 72.875 | 66.992 | 62.138 | 60.914 |
| −0.008 | 68.373 | 55.317 | 72.819 | 67.115 | 61.830 | 59.193 |
| −0.010 | 70.032 | 52.934 | 72.851 | 67.253 | 61.528 | 57.574 |
Electric field applied perpendicular to the C–O bond
The BDE vary slowly and linearly when the electric field is applied in a perpendicular direction to the C–O bond of the most stabilized radical in the plane of the molecule (perpendicular to other two axes; Fig. 1). It can be observed from Table 1 that the change in BDE is less than 1 kcal mol−1 with an increment of 0.002 a.u. of electric field. For instance, the BDE value for gallic acid increases to 82.499 kcal mol−1 at 0.002 a.u. of electric field (compared to 81.869 kcal mol−1 in the absence of electric field) while decreases to 81.232 kcal mol−1 on applying the same strength of field in opposite direction. Again, the value of BDE for gallic acid increases to 84.696 kcal mol−1 at 0.010 a.u. of electric field while, decreases to 78.301 kcal mol−1 on applying the same strength of field in opposite direction. Interestingly, in case of caffeic acid, on applying electric field of 0.010 a.u., BDE decreases to 73.118 kcal mol−1 while increases to 80.780 kcal mol−1 in reverse direction (Table 1). On comparing these BDE values with those obtained along the C–O bond direction, it can be observed that the change in BDE with respect to zero field is less in the perpendicular direction (Table 1).The IE for gallic acid increases on increasing electric field in +y axis (Fig. 1) and decreases with electric field applied in opposite direction. For caffeic acid also IE increases with electric field in +x axis (Fig. 1) and the reverse trend is observed for opposite direction. This variation is smaller than that obtained on applying electric field in C–O bond direction, in a similar manner to that of BDE values (Table 2).
PDE for gallic acid did not show much deviation from the zero field value on applying the electric field in this direction (along both +ve and −ve y axis; Fig. 1). On the contrary, highest deviation from zero field value of PDE is obtained for caffeic acid on applying electric field in the perpendicular to C–O bond. PDE decrease to 187.552 kcal mol−1 when the electric field increase to 0.010 a.u. in +x axis while increases to 215.912 kcal mol−1 on increasing the field in the opposite direction (Table 3).
The PA values show same trend as that shown by PDE for the two systems in the presence of the electric field applied perpendicular to the C–O bond (Table 4).
ETE deviates from the zero field value for both gallic and caffeic acids on varying the electric field in this direction. However, this deviation is smaller than that obtained on applying electric field along the C–O bond. For gallic acid, ETE increases with electric field along +y axis and for caffeic acid it increases in +x axis (Table 5). The reverse order is obtained for the both along the opposite directions, separately.
Electric field applied perpendicular to the molecular plane
It can be observed that all the reaction enthalpies for both the antioxidant molecules remain almost invariant with the applied external electric field in the perpendicular direction to the molecular plane (Tables 1–5). However, in case of gallic acid, there is a change in ETE and PA values when the electric field is changed from 0.004 a.u. to higher values (perpendicular to the molecular plane). This is because of a conformational change of one of the O–H bond during the optimization of the anion of gallic acid only.It is expected that the external electric field would interact with the dipole of the molecule, as the molecules are polar in nature. On observation, it is found that the dipoles of gallic and caffeic acids change its direction with the change in the external electric field (see ESI†). Thus, the variation of antioxidant properties may be partially explained from the change in the component of the dipole moment vector along the C–O bond. It is found that when the electric field is applied in the perpendicular direction to the C–O bond in the plane of the molecule, the component of the dipole for both the molecules vary slowly, as compared to the variation of the component of the dipole when the external electric field is applied along the C–O bond (see ESI†). This may explain the significant change in the antioxidant properties of the molecules when the external electric field is applied along the C–O bond. Furthermore, the component of the dipole along the C–O bond in both the molecules remain almost invariant, when the electric field is applied perpendicular to the molecular plane and therefore, electric field has no effect on the antioxidant properties of both the molecules when the external electric field is applied along this direction.
Effect of field on the O–H bond length
Now, we would like to discuss the effect of the external electric field on the O–H bond, from which a stable phenoxyl radical is generated by abstraction of H-atom (i.e., the 4-OH bond). The geometries of gallic and caffeic acids have been fully optimized at LC-BLYP/6-311++G(3df,2p) level of theory with each of the external electric field value applied along the C–O bond. The length of the O–H bond with change in field is presented in Table 6. The length of the O–H bond gives a measure of the O–H bond strength which in turn, gives a qualitative measure of BDE and PA. It can be observed from Table 6 that for both the molecules, the O–H bond length marginally decreases (i.e. bond strength increases) with the increase in the electric field applied towards the C–O bond, whereas the O–H bond length increases (i.e. bond strength decreases) with increase in electric field in the reverse direction. For instance, the O–H bond length at zero field, 0.01 a.u. towards the C–O bond, and 0.01 a.u. in the opposite direction, for gallic acid, are 0.9646 Å, 0.9638 Å and 0.9669 Å, respectively, whereas for caffeic acid, the values are 0.9600 Å, 0.9583 Å and 0.9635 Å, respectively (Table 6). It is known that the BDE depends on the bond strength as well as the radical stability. So, it is expected that the BDE will show a similar trend with the bond strength, however, we found that they actually show an opposite behavior i.e., when the length of the O–H bond increase the BDE increases. This may be due to the fact that the increase in radical stability of the phenoxyl radical with electric field is much more than the increase in bond strength of the O–H bond, which in turn decreases the BDE with the increase in the electric field and vice versa. This may be validated from the radical stabilization energy (RSE)58 of the phenoxyl radical calculated from the following equation:| RSE = H(ArOH) + H(OH˙) − H(ArO˙) − H(H2O) | (7) |
| Electric field (in a.u.) | O–H bond length (Å) | RSE (kcal mol−1) | ||
|---|---|---|---|---|
| GA | CA | GA | CA | |
| 0.010 | 0.9669 | 0.9635 | 29.928 | 31.902 |
| 0.008 | 0.9663 | 0.9626 | 31.431 | 33.955 |
| 0.006 | 0.9658 | 0.9618 | 32.939 | 36.023 |
| 0.004 | 0.9653 | 0.9611 | 34.452 | 38.112 |
| 0.002 | 0.9649 | 0.9605 | 35.996 | 40.231 |
| 0.000 | 0.9646 | 0.9600 | 37.519 | 42.381 |
| −0.002 | 0.9644 | 0.9595 | 39.059 | 44.586 |
| −0.004 | 0.9641 | 0.9591 | 40.612 | 46.851 |
| −0.006 | 0.9640 | 0.9588 | 42.182 | 49.193 |
| −0.008 | 0.9639 | 0.9585 | 43.768 | 51.629 |
| −0.010 | 0.9638 | 0.9583 | 45.374 | 54.169 |
It can be observed from the RSE values that the radical stability of the phenoxyl radical increases with the increase in the external electric field along the C–O bond. For instance, the RSE of the phenoxyl radical of gallic and caffeic acids increases from 37.519 kcal mol−1 and 42.381 kcal mol−1 at zero field, respectively, to 45.374 kcal mol−1 and 54.169 kcal mol−1 at 0.010 a.u. external electric field applied along the C–O bond (Table 6).
Performance of range-separated density functionals
We chose seven range-separated density functionals LC-BLYP, LC-ωPBE, ωB97, ωB97X, ωB97XD, CAM-B3LYP and M11 along with hybrid B3LYP and semi-empirical M06-2X functionals in calculating the BDE of the two antioxidant molecules in the presence of the electric field applied along the C–O bond. Here, the BDE, reported in Table 7, for each functional is calculated from the molecular enthalpy at 6-311++G(3df,2p) which includes the thermal contributions to the enthalpy (in which the vibrational contributions include zero-point vibrational energy) at 298.15 K. We chose to evaluate the performance of the functionals only on BDE, as calculations of the other properties (PDE, IE, PA and ETE) require the experimental enthalpy of proton and electron at different field value. It is known that the hybrid functionals contain a fraction of HF exchange in the whole range, whereas the range-separated functionals contain 100% HF exchange in the long-range. In order to evaluate the performance of the density functionals, we have calculated the mean signed error (MSE), mean absolute error (MAE) and root mean squared error (RMSE) with respect to the composite CBS-QB3 method (Table 7 and Fig. 3).| Electric field | CBS-QB3 | B3LYP | M06-2X | LC-BLYP | LC-ωPBE | ωB97 | ωB97X | ωB97XD | M11 | CAM-B3LYP |
|---|---|---|---|---|---|---|---|---|---|---|
| Gallic acid | ||||||||||
| 0.010 | 90.34 | 86.70 | 91.56 | 91.00 | 86.41 | 86.60 | 87.42 | 87.94 | 92.35 | 88.60 |
| 0.008 | 88.62 | 84.76 | 89.76 | 89.20 | 84.62 | 84.84 | 85.64 | 86.11 | 90.55 | 86.74 |
| 0.006 | 86.90 | 82.86 | 87.95 | 87.38 | 82.82 | 83.08 | 83.84 | 84.25 | 88.74 | 84.87 |
| 0.004 | 85.17 | 80.95 | 86.13 | 85.56 | 81.03 | 81.28 | 82.00 | 82.42 | 86.92 | 83.01 |
| 0.002 | 83.45 | 79.04 | 84.31 | 83.71 | 79.22 | 79.47 | 80.16 | 80.58 | 85.10 | 81.14 |
| 0.000 | 81.69 | 77.12 | 82.47 | 81.87 | 77.41 | 77.70 | 78.36 | 78.71 | 83.27 | 79.26 |
| −0.002 | 79.89 | 75.20 | 80.62 | 80.02 | 75.58 | 75.95 | 76.57 | 76.86 | 81.43 | 77.38 |
| −0.004 | 78.05 | 73.26 | 78.77 | 78.15 | 73.74 | 74.16 | 74.73 | 74.97 | 79.59 | 75.48 |
| −0.006 | 76.19 | 71.32 | 76.90 | 76.27 | 71.89 | 72.31 | 72.83 | 72.99 | 77.73 | 73.57 |
| −0.008 | 74.32 | 69.36 | 75.01 | 74.37 | 70.02 | 70.41 | 70.90 | 70.98 | 75.84 | 71.65 |
| −0.010 | 72.45 | 67.38 | 73.11 | 72.45 | 68.13 | 68.49 | 68.95 | 68.97 | 73.93 | 69.70 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Caffeic acid | ||||||||||
| 0.010 | 87.86 | 86.23 | 90.61 | 89.03 | 85.08 | 85.37 | 86.40 | 87.28 | 91.02 | 87.54 |
| 0.008 | 85.63 | 83.63 | 88.32 | 86.67 | 82.74 | 83.05 | 84.02 | 84.81 | 88.70 | 85.08 |
| 0.006 | 83.40 | 81.05 | 85.99 | 84.30 | 80.40 | 80.72 | 81.66 | 82.42 | 86.35 | 82.62 |
| 0.004 | 81.16 | 78.46 | 83.63 | 81.90 | 78.04 | 78.38 | 79.29 | 80.02 | 83.97 | 80.14 |
| 0.002 | 78.88 | 75.85 | 81.23 | 79.47 | 75.65 | 76.02 | 76.90 | 77.57 | 81.55 | 77.64 |
| 0.000 | 76.57 | 73.20 | 78.77 | 77.01 | 73.23 | 73.61 | 74.46 | 75.05 | 79.08 | 75.10 |
| −0.002 | 74.20 | 70.48 | 76.23 | 74.49 | 70.76 | 71.15 | 71.95 | 72.45 | 76.55 | 72.50 |
| −0.004 | 71.76 | 67.69 | 73.65 | 71.91 | 68.22 | 68.62 | 69.37 | 69.78 | 74.60 | 69.84 |
| −0.006 | 69.25 | 64.81 | 70.92 | 69.26 | 65.61 | 66.03 | 66.72 | 67.03 | 71.23 | 67.10 |
| −0.008 | 66.64 | 61.82 | 68.08 | 66.51 | 62.92 | 63.30 | 63.97 | 64.18 | 68.42 | 64.25 |
| −0.010 | 63.85 | 58.68 | 65.15 | 63.65 | 60.14 | 60.47 | 61.07 | 61.27 | 65.53 | 61.28 |
| MSE | — | −3.93 | 1.49 | 0.36 | −3.75 | −3.42 | −2.68 | −2.26 | 2.10 | −1.90 |
| MAE | — | 3.93 | 1.49 | 0.39 | 3.75 | 3.42 | 2.68 | 2.26 | 2.10 | 1.90 |
| RMSE | — | 4.06 | 1.66 | 0.51 | 3.79 | 3.46 | 2.76 | 2.41 | 2.17 | 2.03 |
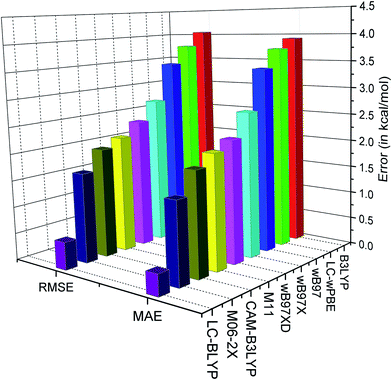 | ||
| Fig. 3 Plot of MAE and RMSE (in kcal mol−1) in reproducing the O–H BDE for different range-separated functionals. | ||
It is observed from the MAE that the tested functionals compute BDE in the presence of the external electric field within an accuracy of 4 kcal mol−1. The best performance is found for the LC-BLYP range-separated functional with the range-separation parameter (μ) of 0.47 Bohr−1 (MAE = 0.39 kcal mol−1 and RMSE = 0.51 kcal mol−1). It can also be observed that the LC-BLYP slightly overestimates the BDE. On the other hand, it can be observed from the MSE (Table 7) that B3LYP, CAM-B3LYP, ωB97, ωB97X, ωB97XD and LC-ωPBE underestimate the BDE values. B3LYP, which is a hybrid functional with 20% HF exchange, shows inferior results in computing the BDE in the presence of the external electric field (MAE and RMSE are 3.93 and 4.06 kcal mol−1, respectively). However, CAM-B3LYP, which is the range separated version of B3LYP, shows lower error than B3LYP (MAE and RMSE are 1.90 and 2.03 kcal mol−1, respectively). On the other hand, the M06-2X functional which is parameterized for calculating thermodynamical property, is found to perform slightly better (MAE = 1.49 kcal mol−1 and RMSE = 1.66 kcal mol−1) than CAM-B3LYP, ωB97, ωB97X, ωB97XD, LC-ωPBE and M11 functionals. Furthermore, the M11 functional, with μ = 0.25 Bohr−1, performs better than the B3LYP (MAE = 2.10 kcal mol−1 and RMSE = 2.17 kcal mol−1) functional. Moreover, the MAE and RMSE values of ωB97 are 3.42 and 3.46 kcal mol−1, respectively, whereas in case of ωB97X they are 2.68 and 2.76 kcal mol−1, respectively (Table 7). We know that ωB97X is a range-separated hybrid with μ = 0.30 Bohr−1 and includes almost 15% of HF exchange in the short-range, whereas ωB97 is range-separated functional with μ = 0.40 Bohr−1. The slightly better performance of ωB97X over ωB97 may be attributed to the inclusion of short-range HF exchange in ωB97X. However, ωB97XD performs slightly better than ωB97X in reproducing BDE due to inclusion of dispersion correction in ωB97XD. It may also be noted that the similar performance of ωB97 and LC-ωPBE may be attributed to the equal value of μ in both the functionals. However, their slight difference in the BDE values may be due to their different functional forms.
Conclusion
In conclusion, we have studied the variation of the antioxidant properties, such as BDE, IE, PDE, PA and ETE, with the external electric field for gallic and caffeic acids. The external electric field is applied (i) along the C–O bond of the most stable phenoxyl radical, produced after the abstraction of H atom; (ii) perpendicular to the C–O bond of the most stable phenoxyl radical, and in the plane of the ring; (iii) perpendicular to the molecular plane. It is found that there is a significant deviation in the antioxidant properties when the electric field is applied along the C–O bond, which may be explained from the interaction of the dipoles with the external electric field. It is known that lower value of BDE, IE, PDE, PA and ETE indicates better antioxidant properties. From our calculations, it is found that, in case of gallic acid, BDE, PDE and PA decreases with increase in the electric field along the C–O bond, whereas IE and ETE decreases with increase in the electric field in the opposite direction. On the other hand, in case of caffeic acid, BDE, IE and ETE decreases with decrease in the electric field along the C–O bond, whereas PDE and PA decreases with increase in the electric field in the opposite direction. Thus, it may be concluded that the antioxidant property of gallic and caffeic acids can be tuned by the application of the electric field. It can also be concluded that the 4O–H bond strength, measured from the O–H bond length and used as a qualitative measure of antioxidant property, decreases with increase in electric field. Furthermore, the performance of range-separated functional are tested in reproducing the O–H BDE in the presence of an external electric field applied along the C–O bond. It is found that the LC-BLYP reproduce the O–H BDE with high accuracy.Acknowledgements
MPB acknowledges the Council of Scientific and Industrial Research (CSIR), New Delhi for his research fellowship. RK acknowledges the SERB, Department of Science and Technology (DST), New Delhi for financial support [SB/FT/CS-132/2013].References
- N. Babbar, H. S. Oberoi and S. K. Sandhu, Crit. Rev. Food Sci. Nutr., 2015, 55, 319–337 CrossRef PubMed.
- B. B. Aggarwal, A. Bhardwaj, R. S. Aggarwal, N. P. Seeram, S. Shishodia and Y. Takada, Anticancer Res., 2004, 24, 2783–2840 CAS.
- Y. Levites, O. Weinreb, G. Maor, M. B. H. Youdim and S. Mandel, J. Neurochem., 2001, 78, 1073–1082 CrossRef CAS.
- D. Bagchi, C. K. Sen, S. D. Ray, D. K. Das, M. Bagchi, H. G. Preuss and J. A. Vinson, Mutat. Res., 2003, 523–524, 87–97 CrossRef CAS.
- F. M. D. Cunha, D. Duma, J. Assreuya, F. C. Buzzi, R. Niero, M. M. Campos and J. B. Calixto, Free Radical Res., 2004, 38, 1241–1253 CrossRef PubMed.
- B. Halliwell, Biochem. Soc. Trans., 2007, 35, 1147–1150 CrossRef CAS PubMed.
- V. I. Lushchak, Chem.-Biol. Interact., 2014, 224, 164–175 CrossRef CAS PubMed.
- M. Carocho and I. C. F. R. Ferreira, Food Chem. Toxicol., 2013, 51, 15–25 CrossRef CAS PubMed.
- M. Strlič, T. Radovič, J. Kolar and B. Pihlar, J. Agric. Food Chem., 2002, 50, 6313–6317 CrossRef PubMed.
- M. N. Franco, T. Galeano-Díaz, Ó. López, J. G. Fernández-Bolaños, J. Sánchez, C. de Miguel, M. V. Gil and D. Martín-Vertedor, Food Chem., 2014, 163, 289–298 CrossRef PubMed.
- J. Ponomarenko, P. Trouillas, N. Martin, T. Dizhbite, J. Krasilnikova and G. Telysheva, Phytochemistry, 2014, 103, 178–187 CrossRef CAS PubMed.
- J. Azevedo, J. Oliveira, L. Cruz, N. Teixeira, N. F. Brás, V. D. Freitas and N. Mateus, J. Agric. Food Chem., 2014, 62, 7002–7009 CrossRef CAS PubMed.
- C. Manach, A. Scalbert, C. Morand, C. Rémésy and L. Jiménez, Am. J. Clin. Nutr., 2004, 79, 727–747 CAS.
- L. Bravo, Nutr. Rev., 1998, 56, 317–333 CrossRef CAS PubMed.
- V. M. Moo-Huchin, I. Moo-Huchin, R. J. Estrada-León, L. Cuevas-Glory, I. A. Estrada-Mota, E. Ortiz-Vázquez and D. Betancur-Ancona, Food Chem., 2015, 166, 17–22 CrossRef CAS PubMed.
- D. M. Maestri, V. Nepote, A. L. Lamarque and J. A. Zygadlo, Phytochemistry, 2006, 105 CAS . ISBN: 81-308-0034-9.
- G. Mazzone, N. Malaj, A. Galano, N. Russo and M. Toscano, RSC Adv., 2015, 5, 565–575 RSC.
- M. Leopoldini, T. Marino, N. Russo and M. Toscano, J. Phys. Chem. A, 2004, 108, 4916–4922 CrossRef CAS.
- G. Wang, Y. Xue, L. An, Y. Zheng, Y. Dou, L. Zhang and Y. Liu, Food Chem., 2015, 171, 89–97 CrossRef CAS PubMed.
- M. Leopoldini, N. Russo and M. Toscano, Food Chem., 2011, 125, 288–306 CrossRef CAS PubMed.
- F. Mura, T. Silva, C. Castro, F. Borges, M. C. Zuñiga, J. Morales and C. Olea-Azar, Free Radical Res., 2014, 48, 1473–1484 CrossRef CAS PubMed.
- N. R. Perron and J. L. Brumaghim, Cell Biochem. Biophys., 2009, 53, 75–100 CrossRef CAS PubMed.
- Y. C. Choi, C. Pak and K. S. Kim, J. Chem. Phys., 2006, 124, 094308–094311 CrossRef PubMed.
- S. J. Suresh, A. L. Prabhu and A. Arora, J. Chem. Phys., 2007, 126, 134502–134507 CrossRef CAS PubMed.
- R. Kar, K. R. S. Chandrakumar and S. Pal, J. Phys. Chem. A, 2007, 111, 375–383 CrossRef CAS PubMed.
- R. Parthasarathi, V. Subramanian and P. K. Chattaraj, Chem. Phys. Lett., 2003, 382, 48–56 CrossRef CAS PubMed.
- R. Kar and S. Pal, Theor. Chem. Acc., 2008, 120, 375–383 CrossRef CAS.
- R. Kar and S. Pal, in Chemical Reactivity: A Density Functional View, ed. P. K. Chattaraj, Taylor & Fransis, CRC Press, 2008, p. 363 Search PubMed.
- K. R. S. Chandrakumar, R. Kar and S. Pal, in Concepts and Methods in Modern Theroetical Chemistry: Electronic Structure and Reactivity, ed. S. K. Ghosh and P. K. Chattaraj, Taylor & Francis, CRC Press, 2013, p. 391 Search PubMed.
- B. J. Dutta and P. K. Bhattacharyya, J. Phys. Chem. B, 2014, 118, 9573–9582 CrossRef CAS PubMed.
- J. Wang, K. Wang, Y. Wang, S. Lin, P. Zhao and G. A. Jones, Food Chem., 2014, 161, 361–366 CrossRef CAS PubMed.
- Y. Fu, X.-Y. Dong, Y.-M. Wang, L. Liu and Q.-X. Guo, Chin. J. Chem., 2005, 23, 474–482 CrossRef CAS PubMed.
- T. M. Gilbert, J. Phys. Chem. A, 2004, 108, 2550–2554 CrossRef CAS.
- H. Z. Yu, F. Fu, L. Zhang, Y. Fu, Z. M. Dang and J. Shi, Phys. Chem. Chem. Phys., 2014, 16, 20964–20970 RSC.
- B. Chan and L. Radom, J. Phys. Chem. A, 2012, 116, 4975–4986 CrossRef CAS PubMed.
- D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 10180–10189 CrossRef CAS PubMed.
- D. J. Tozer, R. D. Amos, N. C. Handy, B. O. Roos and L. Serrano-Andres, Mol. Phys., 1999, 97, 859–868 CrossRef CAS PubMed.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS PubMed.
- A. Savin, in Recent Developments and Applications of Modern Density Functional Theory, ed. J. M. Seminario, Elsevier, Amsterdam, 1996, p. 327 Search PubMed.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151–160 CrossRef CAS.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS PubMed.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109–234117 CrossRef PubMed.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 11363–11370 RSC.
- R. Kar, J.-W. Song, T. Sato and K. Hirao, J. Comput. Chem., 2013, 34, 2353–2359 CrossRef CAS PubMed.
- L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515–1531 CrossRef CAS.
- R. Kar, J.-W. Song and K. Hirao, J. Comput. Chem., 2013, 34, 958–964 CrossRef CAS PubMed.
- R. Kar, M. P. Borpuzari, J.-W. Song and K. Hirao, Mol. Phys. DOI:10.1080/00268976.2015.1059512.
- J.-W. Song, T. Hirosawa, T. Tsuneda and K. Hirao, J. Chem. Phys., 2007, 126, 154105–154111 CrossRef PubMed.
- J. E. Bartmess, J. Phys. Chem., 1994, 98, 6420–6424 CrossRef CAS.
- O. A. Vydrov, J. Heyd, A. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106–074114 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106–084120 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D. 01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- D. J. Henry, C. J. Parkinson, P. M. Mayer and L. Radom, J. Phys. Chem. A, 2001, 105, 6750–6756 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Geometrical coordinates of all the species optimized at different level of theory; calculated thermal enthalpies of all the species at LC-BLYP/6-311++G(3df,2p) (Table S1); total dipole moment (Table S2); component of dipole (Table S3); calculated thermal enthalpies of all the species at different level of theory (Table S4); O–H bond length (Table S5) with different functionals; change of dipole moment (Fig. S1). See DOI: 10.1039/c5ra13462e |
| This journal is © The Royal Society of Chemistry 2015 |