Assessment of two new nitrogen-rich tetrazine derivatives as high performance and safe energetic compounds
Abstract
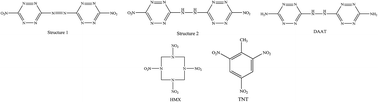
This work introduces two novel nitrogen-rich derivatives of tetrazine, i.e. 1,2-bis(6-nitro-1,2,4,5-tetrazin-3-yl)diazene and 1,2-bis(6-nitro-1,2,4,5-tetrazin-3-yl)hydrazine, as high performance and safe energetic compounds. Reliable methods are used to study the physical, thermodynamic, sensitivity, detonation and combustion properties of these compounds, which include crystal density, condensed phase heat of formation, impact sensitivity, electric spark sensitivity, heat of detonation, detonation temperature, detonation of velocity, pressure detonation, specific impulse, melting point, brisance and power. The predicted properties are also compared with 2,4,6-trinitrotoluene (TNT) and 1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX) as two well-known melt-castable and high performance explosives, respectively. It is shown that these compounds can be seen as interesting organic explosives with relatively high detonation velocity and pressure as well as low sensitivity, and can be used for important industrial applications. Since these new compounds have a relatively high crystal density and melting point as well as great combustion performance, they can also be considered as suitable energetic ingredients in solid propellants. Hydrophobic interactions of these compounds were also computed and compared using the B3PW91/6-31 g(d,p) level of theory as a method for quantum chemical calculations.

 Please wait while we load your content...
Please wait while we load your content...