Closoborate-transition metal complexes for hydrogen storage

Abstract

We report hydrogen uptake capacity of early transition metal (TM) atom (Sc, Ti and V) decorated closoborate (B₆H₆) using density functional theory and second order Møller–Plesset method. Maximum of four hydrogen molecules can be adsorbed on B₆H₆Sc, B₆H₆Ti and B₆H₆V complex with their gravimetric hydrogen uptake of 6.51, 6.36, 6.21 wt% respectively. We have used M06, B3LYP and MP2 methods with 6-311++G** basis set for the study. The Gibbs free energy corrected adsorption energies show that adsorption of four H₂ molecules on B₆H₆Ti and B₆H₆V is energetically favorable whereas it is unfavorable on B₆H₆Sc at 298.15 K at M06/6-311++G** and B3LYP/6-311++G** level. Many-body analysis approach has been used here to study the nature of interaction between adsorbed H₂ molecules and the substrate and that between hydrogen molecules in a complex. The binding energy of B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex is found to be 39.44, 58.43 and 51.03 kcal mol⁻¹ respectively using M06/6-311++G** level of theory. Interaction between inorganic material-metal complexes with adsorbed H₂ molecules is found to be attractive for all the three complexes. The charge transfer between Ti and adsorbed H₂ molecules is more than that for Sc and V. The HOMO–LUMO gap shows that all the three H₂ adsorbed complexes are kinetically stable. The dimers of TM-closoborate complexes in head-to-tail type configuration and multi-transition metal atom decorated closoborate complexes have also been studied. In both the cases number of H₂ molecules adsorbed per TM atom is not affected neither by dimerization nor multi-transition metal atom decoration.

---

1. Introduction

Due to deploying fossil fuels and increasing environmental issues such as global warming it has become necessary to search for a clean and more efficient energy source, its storage options and conversion technologies. Hydrogen is the most abundant element in the universe. It is also the most promising alternative to the carbon based fuels like gasoline. There are no hazardous emissions when it is used as an energy carrier. When used in fuel cells it gives water as the only byproduct. It is a light weight and ideal as a synthetic fuel. For using hydrogen as an energy carrier its production is not a problem but its storage in compact and lightweight package is a challenging task. For hydrogen economy to be a reality searching a material capable of storing hydrogen efficiently for vehicular applications is essential. However it is one of the most difficult challenges. As compared to bulk material nanoscale material and small molecules offer a higher energy storage capacity due to their unique properties such as high surface area, size confinement effect etc.^1–4

Several small organometallic complexes have been considered earlier from hydrogen point of view. It includes transition metal (TM)–acetylene,^5–9 TM–ethylene,^8,10–20 TM–C_nH_n rings and TM–C_nH_m complexes.^21–30 There are several investigations on large inorganic structures as well for hydrogen storage in the form of hydrides. However hydrides require more energy to release hydrogen as it is stored in atomic form. In order to have the fast adsorption and desorption kinetics hydrogen should be stored in a molecular form. As compared to small organometallic complexes, inorganic material-metal (IOM) complexes have received fewer attentions as a hydrogen storage media. Few efforts are made earlier to study IOM complexes from hydrogen storage point of view.^31–40

Hydrogen adsorption in B₆H₂Li₂ has been studied by Srinivasu et al.³¹ and Pathak et al.³² They reported B₆H₂Li₂ as a neutral system. In 1964 Boone has prepared the B₆H₆ ion which is the smallest member of hydroclosoborate family.⁴¹ Chang et al. have investigated the atomistic mechanisms governing hydrogen release and uptake processes in ammonia borane using the density functional theory (DFT) method.³³ The spin-polarized DFT has been used to perform the simulations on 3d transition metal doped borazine.³⁴ Hydrogen storage capacity of alkali metal, alkaline-earth metal and Ti decorated borazine has been investigated using DFT by Li et al.³⁵ They concluded that the alkali metals bound strongly to the borazine. The H₂ uptake capacity of 10.4 wt% was obtained for the Li decorated borazine. Using DFT and Møller–Plesset perturbation theory Pathak et al. have studied the hydrogen uptake of Li and Mg doped boranes.³⁶ Structures and binding energies of hydrogen molecules adsorbed structures were calculated.

Hydrogen storage capacity of Li_mB₆H₆ (m = 1, 2) has been studied by Lu et al. using DFT and observed that the Li atom bound strongly to the substrate.³⁷ Bandaru et al. have constructed the potential energy surface for the H₂ release from ammonia borane with a novel bifunctional cationic ruthenium catalyst based on the sterically bulky β-diketiminato ligand using the DFT.³⁸ Khan and Khan have performed the DFT calculations using hybrid B3PW91 functional to investigate hydrogen storage capacity of Ti, Cr, and Fe doped borazine.³⁹ They concluded that the hydrogen storage capability of Ti–B₃N₃H₆ in its quintet state is half than the triplet state and the quintet state is unfavourable for the hydrogen storage. Samolia and Kumar have studied the hydrogen trapping efficiency of a metal functionalized BN system at various high electron density sites using DFT at M05-2X/6-311G+(d) level of theory.⁴⁰ Zhang et al. have studied Ti substituted boranes computationally for hydrogen storage applications.⁴² They predicted the hydrogen storage capacity of B₅H₅Ti and its TiH substituted analogue B₄H₄Ti₂H₂ as 8.6 and 10 wt% respectively with respective molecular hydrogen binding energy as −23.5 and −35 kJ mol⁻¹ per H₂ molecule. Kumar et al. have modified the metal–organic framework by incorporating transition metal through –OH and –SH functionalization of triphenyl linkers to improve the hydrogen storage capacity of metal–organic framework.⁴³ They applied atoms in molecules theory to characterize the nature of interaction between H₂ and metal centres. Their calculated interaction energy value per H₂ varies from −5.47 to −15.67 kcal mol⁻¹ and is suitable for room temperature hydrogen storage.

Most of the studies on hydrogen storage capacity of IOM complexes have been carried out either with alkali metal or alkaline earth metal doped inorganic material. However it has been observed that hydrogen adsorption on alkali or alkaline earth metal doped organic substrate is energetically unfavorable and these materials are not suitable as hydrogen storage media.^7,9 This is true for wide range of temperature – room temperature, below as well as above room temperature. On the other hand early TM doped systems are good options for hydrogen storage. Therefore we have studied here hydrogen storage capacity of early TM doped inorganic material.

The aim of this work is to study hydrogen adsorption on TM–closoborate (TM = Sc, Ti and V) complexes using DFT and wave function method. The TM–closoborates considered here are B₆H₆Sc, B₆H₆Ti and B₆H₆V. Using Gibbs free energy corrected hydrogen adsorption energies we have suggested a temperature range over which H₂ adsorption is possible on these complexes. Furthermore, the interaction energies between hydrogen molecules and IOM complexes as well as that between different hydrogen molecules in a complex are also studied.

2. Computational details

The geometry optimization of TMB₆H₆(nH₂) (TM = Sc, Ti and V) complexes have been carried out using DFT with Becke's three parameter hybrid functional with LYP correlation functional (B3LYP),^44–46 hybrid functional of Truhlar and Zhao (M06)⁴⁷ and second order Møller–Plesset (MP2) method.⁴⁸ We have used 6-311++G** basis set for all the calculations. All calculations were performed using Gaussian 09 suit of programs.⁴⁹ Vibrational frequencies are also obtained at the same level of theory. Many-body analysis technique has been used to study nature of interaction between different molecules in hydrogen adsorbed complexes and contribution from many-body energies to the binding energy of a respective complex.^50–53

Many-body interaction energies

The decomposition of total energy of a complex can be written aswhere E(i), E(ij), E(ijk), E(ijkl) and E(ijklm) are the energies of various monomers, dimers, trimers, tetramers and pentamers respectively in a complex. E_IOM and E_H2 are the energies of isolated IOM compound and hydrogen molecule respectively. Here u is the number of hydrogen molecules adsorbed in a complex. The pair wise basis set superposition error (BSSE) corrected two-body interaction energies and higher three-body, four-body, etc. interaction energies are defined as:

Δ²E_c(ij) = E(ij) − {E(i) + E(j)} (2)

Δ³E_c(ijk) = E(ijk) − {E(i) + E(j) + E(k)} − {Δ²E(ij) + Δ²E(ik) + Δ²E(jk)} (3)

Δ⁴E_c(ijkl) = E(ijkl) − {E(i) + E(j) + E(k) + E(l)} − {Δ²E(ij) + Δ²E(ik) + Δ²E(il) + Δ²E(jk) + Δ²E(jl) + Δ²E(kl)} − {Δ³E(ijk) + Δ³E(ijl) + Δ³E(ikl) + Δ³E(jkl)} (4)

and so on.

Sum of relaxation energy, two-body energy, three-body energy, four-body energy, and five-body energy gives the binding energy of a complex. The BSSE corrected total energy can be calculated as suggested by Valiron and Mayer.⁵⁴

3. Results and discussions

We have first optimized the geometries of B₆H₆TM (TM = Sc, Ti, V) complexes. The B₆H₆TM structure has six radially bonded H atoms attached to the B atoms at the vertices of an octahedron. The TM atoms Sc, Ti, V are counter-positioned on top of the face centered sites. Optimized structures of B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) at M06/6-311++G** level of theory are shown in Fig. 1. Maximum of four H₂ molecules are adsorbed on B₆H₆Sc, B₆H₆Ti and B₆H₆V complex thereby showing their H₂ uptake capacity of 6.51, 6.36, 6.21 wt% respectively. It is little higher than the target set by U. S. Department of Energy by 2015 (5.5 wt%). Structural parameters of H₂ adsorbed complexes are presented in Table 1. The bond between B₆H₆ and transition metal is little elongated upon H₂ adsorption for all the three cases. The elongation is more for B₆H₆V complex than B₆H₆Sc and B₆H₆Ti. Hydrogen molecules are adsorbed at shorter distance in B₆H₆V(4H₂) than B₆H₆Sc(4H₂) and B₆H₆Ti(4H₂) complexes.

Fig. 1 Optimized structures of (a) B₆H₆Sc(4H₂) (b) B₆H₆Ti(4H₂) (c) B₆H₆V(4H₂) at M06/6-311++G** level.

Table 1 Structural parameters (Å) for B₆H₆TM(4H₂) (TM = Sc, Ti, V) obtained at M06/6-311++G** and B3LYP/6-311++G** levels. The values in the parenthesis are obtained using B3LYP method

Assignments	B6H6Sc(4H2)	B6H6Ti(4H2)	B6H6V(4H2)
B6H6-TM	2.29(2.32)	2.23(2.25)	2.25(2.28)
TM-1H2	2.21(2.25)	2.03(2.06)	1.83(1.83)
TM-2H2	2.26(2.30)	2.04(2.13)	1.98(1.99)
TM-3H2	2.24(2.25)	1.91(1.93)	1.81(1.84)
TM-4H2	2.14(2.17)	1.91(1.92)	1.87(1.94)

---

Not only bond between B₆H₆ and transition metal but the H–H bond lengths of H₂ molecules are also changed upon adsorption. The calculated H–H bond length for the isolated H₂ molecule is found to be 0.750 Å at M06/6-311++G** level of theory. In B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complexes the H–H bond lengths are in a range of 0.769–0.786 Å, 0.785–0.824 Å and 0.782–0.821 Å respectively. These H–H bond lengths are longer in H₂ adsorbed complexes than that of free H₂ molecule. It indicates that there is a Kubas interaction between transition metal atom and adsorbed H₂ molecules.⁴³ This elongation in H–H bond length than the free H₂ molecule is due to the charge transfer from d orbital of the transition metal atom to the adsorbed H₂ molecules.

Thermodynamic calculations have been carried out to evaluate the averaged H₂ adsorption energy. The averaged adsorption energy with Gibbs free energy correction (ΔE_G) for ‘n’ number of H₂ adsorbed TM : B₆H₆ complex is calculated as:

ΔE_G = {E_G[IOM] + nE_G[H₂] − E_G[IOM(H₂)_n]}/n

here E_G[X] stands for the total energy of a complex X with Gibbs free energy correction.

E_G[X] and Gibbs free energy correction E_{G corr}[X] are given by:

E_G[X] = E[X] + E_{G corr}[X], and

E_{G corr}[X] = E_zpe[X] + E_thm[X] + k_BT − TS[X]

here E[X] is the total energy of a complex X, E_zpe[X] is the zero-point energy, E_thm[X] is the energy due to sum of translational, rotational and vibrational motion of X, k_B is the Boltzmann's constant, and S[X] is the sum of entropy for translational, rotational and vibrational motion of X.

Table 2 gives averaged adsorption energies without zero point energy correction (ΔE), with zero point energy correction (ΔE_zpe) and with Gibbs free energy correction (ΔE_G) at 298.15 K for B₆H₆TM(4H₂) (TM = Sc, Ti, V) complexes at M06/6-311++G**, B3LYP/6-311++G** and MP2/6-311++G** levels. The Gibbs free energy corrected adsorption energies show that adsorption of four H₂ molecules on B₆H₆Ti and B₆H₆V is energetically favorable whereas it is unfavorable on B₆H₆Sc at 298.15 K using M06 and B3LYP methods. Using MP2 method the adsorption of four H₂ molecules on B₆H₆Sc and B₆H₆V complex is thermodynamically unfavorable where as it is favorable for B₆H₆Ti complex at room temperature. In order to find a temperature range over which H₂ adsorption on these three complexes is energetically favorable, we have calculated Gibbs free energy corrected H₂ adsorption energies for different temperatures. Temperature dependent ΔE_G values are plotted in Fig. 2 using M06/6-311++G** and B3LYP/6-311++G** levels. As can be seen from Fig. 2 adsorption of four H₂ molecules on B₆H₆Ti and B₆H₆V is energetically favorable for all the temperatures considered here at M06/6-311++G** as well as B3LYP/6-311++G** level of theory. Adsorption of four H₂ molecules on B₆H₆Sc is energetically favorable below 270 K and 160 K at M06/6-311++G** and B3LYP/6-311++G** level respectively.

Table 2 Average hydrogen adsorption energies without zpe correction (ΔE), with zpe correction (ΔE_zpe) and Gibbs free energy correction (ΔE_G) at 298.15 K for B₆H₆TM(4H₂) (TM = Sc, Ti, V) complex at M06/6-311++G**, B3LYP/6-311++G** and MP2/6-311++G** levels of theory. All energies are in eV

Complex	M06/6-311++G**			B3LYP/6-311++G**			MP2/6-311++G**
	ΔE	ΔEzpe	ΔEG	ΔE	ΔEzpe	ΔEG	ΔE	ΔEzpe	ΔEG
B6H6Sc(4H2)	0.42	0.26	−0.03	0.26	0.13	−0.15	0.25	0.12	−0.16
B6H6Ti(4H2)	0.63	0.45	0.16	0.55	0.36	0.07	0.57	0.39	0.09
B6H6V(4H2)	0.55	0.37	0.08	0.35	0.18	0.06	0.30	0.09	−0.21

---

Fig. 2 Temperature dependent Gibbs free energy corrected H₂ adsorption energy for B₆H₆Sc(H₂)₄, B₆H₆Ti(H₂)₄ and B₆H₆V(H₂)₄ at M06/6-311++G** and B3LYP/6-311++G** levels.

For ideal hydrogen storage the H₂ desorption from host material is necessary at ambient conditions. The H₂ desorption temperature from B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complexes is obtained using ΔE_zpe and the van't Hoff equation⁵⁵ as

T_D = (ΔE_zpe/k_B)(ΔS/R − ln P)⁻¹

where k_B is the Boltzmann constant (1.38 × 10⁻²³ J K⁻¹), R the gas constant (8.31 J K⁻¹ mol⁻¹), ΔS the change in the H₂ entropy from gas to liquid phase and P the equilibrium pressure P (1 atm). Using ΔS from ref. 56 and values of ΔE_zpe calculated at M06/6-311++G** level of theory from Table 2, minimum and maximum H₂ desorption temperatures (T_D) from the H₂ adsorbed complexes are calculated. Minimum H₂ desorption temperature for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂), B₆H₆V(4H₂) is found to be 332 K, 574 K and 472 K respectively whereas maximum desorption temperature for the respective complexes is 650 K, 1288 K and 956 K using M06/6-311++G** level of theory. The maximum desorption temperatures (T_{D max}) or the temperatures to desorb all the adsorbed H₂ molecules from the host material are calculated using ΔE_zpe values of the B₆H₆Sc(1H₂), B₆H₆Ti(1H₂) and B₆H₆V(1H₂) complexes. It is found that the maximum desorption temperature is higher for B₆H₆Ti(4H₂) complex relative to other two complexes. This is because when the first H₂ molecule is adsorbed on B₆H₆Ti complex more charge get transferred from Ti to the only adsorbed H₂ molecule and due to the Kubas interaction the H–H bond length gets more elongated. As the H–H bond length increases corresponding ΔE_zpe also increases and as a consequence desorption temperature increases as well. Desorption temperatures using other two methods are also given in Table 3. The value for maximum desorption of B₆H₆V(4H₂) complex is not given because its ΔE_zpe value is found to be negative.

Table 3 Calculated minimum (T_{D min}) and maximum (T_{D max}) H₂ desorption temperatures (in Kelvin) for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complexes

Complex	M06/6-311++G**		B3LYP/6-311++G**		MP2/6-311++G**
	(TD min)	(TD max)	(TD min)	(TD max)	(TD min)	(TD max)
B6H6Sc(4H2)	332	650	166	459	153	357
B6H6Ti(4H2)	574	1288	459	1186	497	2295
B6H6V(4H2)	472	956	230	383	115	—

---

Kinetic stability of H₂ adsorbed complexes is verified by using a gap between Highest Occupied Molecular Orbital (HOMO) and Lowest Unoccupied Molecular Orbital (LUMO) at M06/6-311++G**, B3LYP/6-311++G** and MP2/6-311++G** levels. The HOMO–LUMO gap is plotted for different H₂ adsorbed complexes in Fig. 3 at all three the levels of theories used here. The HOMO–LUMO gap for the maximum H₂ adsorbed B₆H₆Sc and B₆H₆Ti complexes are higher than that for the respective isolated complexes (before H₂ adsorption). It indicates more kinetic stability of H₂ adsorbed B₆H₆Sc and B₆H₆Ti complexes than respective isolated IOM complex. There is negligible change in HOMO–LUMO gap for isolated B₆H₆V after maximum H₂ adsorption on it. The stability of H₂ adsorbed complexes is also verified by calculating vibrational frequencies for the three complexes. Table 4 shows selected vibrational frequencies and their assignment for H₂ adsorbed complexes using M06 and B3LYP method. There are no imaginary frequencies for all the three complexes studied indicating that these complexes are quantum mechanically stable.

Fig. 3 HOMO–LUMO gap for B₆H₆Sc(H₂)₄, B₆H₆Ti(H₂)₄ and B₆H₆V(H₂)₄ at M06/6-311++G**, B3LYP/6-311++G** and MP2/6-311++G** levels.

Table 4 Selected vibrational modes (in cm⁻¹) for B₆H₆TM(4H₂) (TM = Sc, Ti, V) complexes using M06/6-311++G** and B3LYP/6-311++G** levels of theory. The values in the parenthesis are obtained using B3LYP method

Assignments	B6H6Sc(4H2)	B6H6Ti(4H2)	B6H6V(4H2)
B6H6-TM stretch (sym.)	403(376)	410(472)	336(337)
TM-H stretch (sym.)	544/563/511/685	590/693/859/930(934)	958/999/873(915)
TM-H stretch (asym.)	1183/1258(859/455)	1236/1255/1449/1466(779/778)	1546/1588/1322/1426
H–H stretch	3699/3772/3874//3937	3274/3314/3448/3644	3117/3267/3385/3722
	(4081/3918/4071/3851)	(3137/3293/3426/3500)	(3064/3382/3744/3897)

---

Interaction energies between molecules

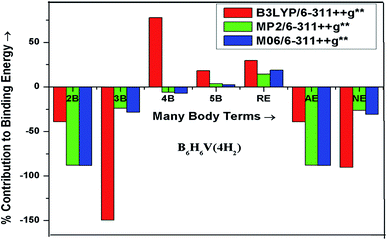
Many-body analysis technique has been used here to calculate various interaction energies for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complexes and are presented in Table 5 at M06/6-311++G** level. The % contribution from many-body energies, additive energy and nonadditive energy to the binding energy of B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complexes is shown in Fig. 4, 5 and 6 respectively at all the three levels of theories used here. As can be seen from Table 4 total two-body energy has major contribution to the binding energy of a respective H₂ adsorbed complex. The binding energy of B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex is found to be 39.44, 58.43 and 51.03 kcal mol⁻¹ respectively at M06/6-311++G** level. This shows that each hydrogen molecule binds to the transition metal atom with energy in a range of 9.86 to 14.6 kcal mol⁻¹ at M06/6-311++G** level of theory. It indicates that the complex considered here are suitable for hydrogen storage. The adsorption energies are within the range of physisorption and chemisorption and we expect fast adsorption and desorption kinetics.

Table 5 Interaction energies and binding energy for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂), B₆H₆V(4H₂) complexes by using the M06/6-311++G** method

Interaction terms	Interaction energy (kcal mol^−1)
	B6H6Sc(4H2)	B6H6Ti(4H2)	B6H6V(4H2)
Two body
IOM–H1	−9.98	−14.63	−15.20
IOM–H2	−11.67	−18.73	−10.08
IOM–H3	−9.56	−21.47	−14.07
IOM–H4	−14.16	−21.59	−12.92
H1–H2	0.25	0.58	0.93
H1–H3	−0.11	−0.05	0.42
H1–H4	−0.11	−0.07	4.28
H2–H3	0.31	3.34	1.21
H2–H4	1.43	3.41	−0.12
H3–H4	−0.12	0.16	0.58
Three body
IOM–H1–H2	1.18	2.37	−2.85
IOM–H1–H3	2.64	2.58	−4.02
IOM–H1–H4	0.82	2.82	−3.41
IOM–H2–H3	1.13	0.13	−1.22
IOM–H2–H4	0.95	0.16	2.08
IOM–H3–H4	1.17	−0.33	−3.74
H1–H2–H3	0.03	−0.32	−0.69
H1–H2–H4	−0.06	−0.26	0.06
H1–H3–H4	−0.02	−0.10	−0.71
H2–H3–H4	−0.01	−0.50	0.04
Four body
IOM–H1–H2–H3	−2.40	−1.87	0.24
IOM–H1–H2–H4	−0.95	−2.05	−2.52
IOM–H1–H3–H4	−1.33	−0.41	0.92
IOM–H2–H3–H4	−1.19	1.18	−2.37
H1–H2–H3–H4	−0.03	−0.04	−0.02
Five body
IOM–H1–H2–H3–H4	1.54	1.04	2.51
Sum of 2-body	−43.72	−69.07	−44.98
Sum of 3-body	7.83	6.56	−14.45
Sum of 4-body	−5.91	−3.20	−3.75
Sum of 5-body	1.54	1.04	2.51
Relaxation energy	0.82	6.25	9.65
Additive energy	−43.72	−69.07	−44.98
Non additive energy	3.46	4.39	−15.69
Binding energy	−39.44	−58.43	−51.03
BSSE corrected total energy	−918.05	−1006.76	−1101.28

---

Fig. 4 Contribution from many-body energies, additive energy, nonadditive energy, relaxation energy to the binding energy of B₆H₆Sc(4H₂) complex. 2B, 3B, 4B, 5B, RE, AE, NE represents total two-body, three-body, four-body, five-body-energy, relaxation energy, additive energy and nonadditive energy respectively.

Fig. 5 Contribution from many-body energies, additive energy, nonadditive energy, relaxation energy to the binding energy of B₆H₆Ti (4H₂) complex. 2B, 3B, 4B, 5B, RE, AE, NE represents total two-body, three-body, four-body, five-body-energy, relaxation energy, additive energy and nonadditive energy respectively.

Fig. 6 Contribution from many-body energies, additive energy, nonadditive energy, relaxation energy to the binding energy of B₆H₆V(4H₂) complex. 2B, 3B, 4B, 5B, RE, AE, NE represents total two-body, three-body, four-body, five-body-energy, relaxation energy, additive energy and nonadditive energy respectively.

Interaction of IOM complex with adsorbed H₂ molecules is found to be attractive for all the three complexes. Total attractive contribution from IOM–H_i two-body interactions to the total two-body interaction energy is 103.8, 110.6 and 116.2% for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively. Total repulsive contribution from H_i–H_j interaction two-body energy terms to the binding energy of a respective complex is 3.8, 10.6 and 16.2%. As we go from B₆H₆Sc to B₆H₆V attractive% contribution from IOM–H_i terms and repulsive% contribution from H_i–H_j terms to the respective total two body energy increases. Though IOM–H_i two-body interaction energies are higher than H_i–H_j interaction energies the latter are not negligible.

Contribution from total three body energy to the binding energy of B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) is found to be 19.85 (repulsive), 11.22 (repulsive) and 28.31 (attractive)% respectively. Three-body energies for which IOM is one of the three body terms contribute about 100.8 (repulsive), 117.9 (repulsive) and 91 (attractive)% to total three body energy for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively. Contribution from H_i–H_j–H_k attractive interaction energy to total three-body energy for the B₆H₆Sc(4H₂) complex is negligible (0.8%) whereas its contribution is 17.9 (attractive) and 9 (attractive)% for the B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively. Most of the IOM–H_i–H_j three-body energies are repulsive in nature except the IOM–H₃–H₄ for B₆H₆Ti(4H₂) and IOM–H₁–H₂, IOM–H₁–H₃, IOM–H₁–H₄, IOM–H₂–H₃ and IOM–H₃–H₄ for B₆H₆V(4H₂) which are attractive in nature.

Similar to total two-body and total three-body energy, total four-body and total five-body energies also contribute significantly to the binding energy of respective complex. Total four-body energy has attractive contribution of 14.98, 5.47 and 7.34% to the binding energy of B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively. Total five body energy contributes repulsively to the binding energy of respective complex and it is about 3.9, 1.8 and 4.9% for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively. In case of four-body energy the contribution from the four-body energy terms H_i–H_j–H_k–H_l is negligible as compared to IOM–H_i–H_j–H_k four-body energy terms. The % of contribution from terms containing IOM as one of the four-body terms is 99.3, 98.4 and 99.5% for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively.

Contribution from the relaxation energy to binding energy of respective complex is also not negligible. It has repulsive contribution of 2.1, 10.7 and 18.9% for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂) and B₆H₆V(4H₂) complex respectively at M06/6-311++G** level. Its contribution increases from B₆H₆Sc to B₆H₆V.

NBO analysis

Natural bond orbital (NBO)⁵⁷ charges are calculated for all the complexes to understand their charge distribution during successive addition of H₂ molecules. To get qualitative picture about charge transfer we calculated the charge on Sc, Ti, V atoms in B₆H₆Sc, B₆H₆Ti, B₆H₆V complexes with successive addition of H₂ molecules using the NBO analysis. The charge on TM atom with successive addition of H₂ molecules is plotted in Fig. 7 at M06/6-311++G** level. Charge on Sc and V atom is positive before H₂ adsorption and remains positive even after adsorption of maximum four H₂ molecules on B₆H₆Sc and B₆H₆V complex. Charge on Ti atom is also positive before adsorption of first H₂ molecule on B₆H₆Ti and becomes negative after adsorption of four H₂ molecules on it. It is observed that charge on Sc before first H₂ adsorption is 1.07 and decreases with successive addition of H₂ molecule up to third H₂ molecule at M06/6-311++G** level. It slightly increases after addition of fourth H₂ molecule. A large change in charge on Ti is observed after H₂ adsorption. Charge on Ti before first H₂ adsorption is 0.91 which becomes −0.54 after fourth H₂ molecule adsorption. The charge on V decreases from 1.06 to 0.18 after adsorption of four H₂ molecules. Charge transfer is more between Ti and adsorbed H₂ molecules than that between Sc and H₂ as well as V and H₂. This is due to the fact that the Ti atom interacts strongly with the adsorbed H₂ molecules than the Sc and V as can be seen from the higher two-body IOM–H_i interaction energies for B₆H₆Ti(4H₂) system than that for B₆H₆Sc(4H₂) and B₆H₆V(4H₂) systems. More the charge transfer between transition metal atom and H₂, more is the elongation in the H–H bond lengths. This is confirmed from more elongation in H–H bond lengths for adsorbed H₂ molecules in B₆H₆Ti(4H₂) complex than the B₆H₆Sc(4H₂) and B₆H₆V(4H₂) complexes.

Fig. 7 Charge on metal atom plotted as a function of number of adsorbed H₂ molecules for B₆H₆Sc(nH₂), B₆H₆Ti(nH₂), B₆H₆V(nH₂) (n = 1–4) complexes at M06/6-311++G** level.

Dimerization of closoborate-TM complex and multi-TM decorated closoborate complexes

We have studied the dimers of closoborate-TM complexes to check whether there is a clustering of transition metal atoms. We have considered here head-to-tail type of dimers and the optimized geometries of one of the three dimers before and after H₂ adsorption are shown in Fig. 8. As can be seen from Fig. 8 there is no clustering of transition metal atoms in case of head-to-tail type of structures for all the three cases before as well as after H₂ adsorption. The number of H₂ molecules adsorbed per TM atom remains four for all the three systems. However H₂ molecules adsorbed on sandwiched TM atom are at little longer distance than that on TM atom which is decorated at one end.

Fig. 8 Head-to-tail type dimers of B₆H₆V (a) before H₂ adsorption (b) after H₂ adsorption at M06/6-311++G** level.

We have also investigated multi-transition metal atom-closoborate complexes and their hydrogen storage capacity. Four transition metal atoms are decorated on closoborate for all the three cases. When four TM atoms are decorated on closoborate we do observed clustering of TM atoms. Fig. 9 shows one of the three structures with decoration of four Sc atoms on closoborate before and after H₂ adsorption. Two pairs of transition metal atom dimers are formed in each case. The Sc–Sc, Ti–Ti and V–V atoms before (after) H₂ adsorption are at a distance of 3.034 (3.154), 2.273 (3.069), 1.871 (2.936) Å from each other respectively in each pair. It indicates that TM–TM bond gets elongated upon H₂ adsorption. Two pairs of Sc–Sc, Ti–Ti and V–V dimers are at a distance of 5.163, 4.880 and 4.528 respectively from each other in H₂ adsorbed complexes. In single TM decorated closoborates, four H₂ molecules are adsorbed per TM atom. Clustering of TM atoms does not affect the number of adsorbed H₂ molecules per TM atom for all the three cases. Total number of H₂ adsorbed on four TM atoms decorated closoborate is sixteen (four H₂ per TM atom) for all the three cases. However two of the sixteen H₂ molecules are dissociated and adsorbed in atomic form one on each TM dimer as shown in Fig. 9. Each TM dimer adsorbs eight H₂ molecules one of which is dissociated.

Fig. 9 B₆H₆ decorated with four Sc atoms (a) before H₂ adsorption (b) after H₂ adsorption at M06/6-311++G** level.

The averaged H₂ adsorption energies for B₆H₆Sc₄(16H₂), B₆H₆Ti₄(16H₂) and B₆H₆V₄(16H₂) complexes without(with) zero point energy correction are found to be 0.52(0.36), 0.59(0.40) and 0.36(0.17) eV respectively. Similar to single TM atom decorated B₆H₆ complexes these energies are within the range of physisorption and chemisorption and we expect fast adsorption and desorption kinetics. The Gibbs free energy corrected adsorption energies for B₆H₆Sc₄(16H₂), B₆H₆Ti₄(16H₂) and B₆H₆V₄(16H₂) complexes are found to be 0.07, 0.10 and −0.13 respectively. It indicates that sixteen H₂ molecule adsorption on four Sc and four Ti decorated closoborates is energetically favorable at ambient conditions whereas it is unfavorable on four V decorated closoborates. The binding energy of B₆H₆Sc₄(16H₂), B₆H₆Ti₄(16H₂) and B₆H₆V₄(16H₂) complex is found to be 195, 219 and 135 kcal mol⁻¹ respectively at M06/6-311++G** level indicating that each hydrogen molecule binds to TM atom with energy in a range of 8.4 to 12.2 kcal mol⁻¹. It indicates that not only single TM atom decorated B₆H₆ complex but four TM atom decorated B₆H₆ complexes are also suitable for hydrogen storage though clustering of TM atoms is observed for the latter.

4. Conclusions

We have studied hydrogen uptake capacity of transition metal decorated closoborate using M06, B3LYP and MP2 methods and 6-311++G** basis set. The number of hydrogen molecules adsorbed on each complex is the same. Contribution from many-body energies to the binding energy of a complex is studied. Many-body analysis for the three complexes reveals that not only two-body but higher many-body energies are also contributing significantly to the binding energy of respective complex. There are no soft modes for the three complexes indicating that these complexes are quantum mechanically stable. Thermochemistry calculations reveal that adsorption of four H₂ molecules on B₆H₆Ti and B₆H₆V is energetically favorable for all the temperatures considered here whereas it is energetically favorable on B₆H₆Sc below 270 K at M06/6-311++G**. Minimum H₂ desorption temperature for B₆H₆Sc(4H₂), B₆H₆Ti(4H₂), B₆H₆V(4H₂) is found to be 332 K, 574 K and 472 K respectively whereas maximum desorption temperature for the respective complexes is 650 K, 1288 K and 956 K using M06/6-311++G** level of theory. Averaged adsorption energy is within the proposed range and affected by the functional employed in DFT calculations. In head-to-tail type of dimers of closoborate-TM complexes there is no clustering of TM atom observed and the number of H₂ molecules adsorbed per TM atom remains four. H₂ molecules adsorbed on sandwiched TM atom are at little longer distance than that on TM atom at one end. In case of four TM atoms decorated closoborate we do observed clustering of TM atoms. Number of H₂ molecules adsorbed per TM atom remains the same with two of the sixteen H₂ molecules are adsorbed in dissociated form.

Acknowledgements

Financial support from C.S.I.R., New Delhi, India (Grant 03/1223) is gratefully acknowledged. We thank CDAC, Pune for providing Bioinformatics Resources and Applications Facility (BRAF).

References

1. http://www.eere.energy.gov/hydrogenandfuelcells/mypp.
2. Solid state hydrogen storage materials and chemistry, ed. G. Walker, Woodhead Publ. Ltd., Cambridge, England, 2008.
3. D. P. Broom, Hydrogen Storage Materials The Characterisation of Their Storage Properties, Springer, 2011.
4. R. A. Varin, T. Czujko and Z. S. Wronski, Nanomaterials for solid state hydrogen storage, Springer, 2009.
5. L. J. Ma, J. Jia, H. S. Wu and Y. Ren, Int. J. Hydrogen Energy, 2013, 38, 16185.
6. M. Li-Juan, J. Jianfeng and H. S. Wu, Int. J. Hydrogen Energy, 2015, 40, 420.
7. V. Kalamse, N. Wadnerkar, A. Deshmukh and A. Chaudhari, Int. J. Hydrogen Energy, 2012, 37, 3727.
8. V. Kalamse, N. Wadnerkar, A. Deshmukh and A. Chaudhari, Int. J. Hydrogen Energy, 2012, 37, 5114.
9. P. Tavhare, V. Kalamse, R. Bhosale and A. Chaudhari, Struct. Chem., 2015, 26, 823.
10. C. S. Liu and Z. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 245419.
11. E. Durgun, S. Ciraci, W. Zhou and T. Yildirim, Phys. Rev. Lett., 2006, 97, 226102.
12. W. Zhou, T. Yildirim, E. Durgun and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085434.
13. N. Wadnerkar, V. Kalamse and A. Chaudhari, Theor. Chem. Acc., 2010, 127, 285.
14. A. Chakraborty, S. Giri and P. K. Chattaraj, Struct. Chem., 2011, 22, 823.
15. A. B. Phillips and B. S. Shivaram, Nanotechnology, 2009, 20, 204020.
16. Y. Okamoto, J. Phys. Chem. C, 2008, 112, 17721.
17. N. He, T. Gao, Z. Zhang, X. Tian and H. Han, J. Mol. Struct.: THEOCHEM, 2009, 916, 147.
18. V. Kalamse, N. Wadnerkar and A. Chaudhari, J. Phys. Chem. C, 2010, 114, 4704.
19. N. Wadnerkar, V. Kalamse, A. B. Phillips, B. S. Shivaram and A. Chaudhari, Int. J. Hydrogen Energy, 2011, 36, 9727.
20. N. Wadnerkar, V. Kalamse and A. Chaudhari, RSC Adv., 2012, 2, 8497.
21. Z. Guo, W. Wu and H. Zhang, Struct. Chem., 2009, 20, 1107.
22. N. Wadnerkar, V. Kalamse and A. Chaudhari, Int. J. Hydrogen Energy, 2011, 36, 664.
23. A. I. Martinez, J. Nano Res., 2009, 5, 113.
24. P. F. Wecka and T. J. D. Kumar, J. Chem. Phys., 2007, 126, 094703.
25. A. B. Phillips, B. S. Shivaram and G. R. Myneni, Int. J. Hydrogen Energy, 2012, 37, 1546.
26. B. Kiran, A. K. Kandalam and P. Jena, J. Chem. Phys., 2006, 124, 224703.
27. Q. Dong, W. Q. Tian, D. L. Chen and C. C. Sun, Int. J. Hydrogen Energy, 2009, 34, 5444.
28. G. Chen, P. Jena and Y. Kawazoe, J. Chem. Phys., 2008, 129, 074305.
29. N. Wadnerkar, V. Kalamse and A. Chaudhari, Struct. Chem., 2013, 24, 369.
30. N. Wadnerkar, V. Kalamse, S. L. Lee and A. Chaudhari, J. Comput. Chem., 2012, 33, 170.
31. K. Srinivasu and S. K. Ghosh, J. Phys. Chem. C, 2011, 115, 1450.
32. B. Pathak, K. Pradhan, T. Hussain, R. Ahuja and P. Jena, ChemPhysChem, 2012, 13, 300.
33. K. Chang, E. Kim, P. F. Weck and D. Tománek, J. Chem. Phys., 2011, 134, 214501.
34. S. A. Shevlina and Z. X. Guo, Appl. Phys. Lett., 2006, 89, 153104.
35. M. Li, J. Li, Q. Sun and Y. Jia, J. Appl. Phys., 2010, 108, 064326.
36. B. Pathak, K. Pradhan, K. T. Hussain, R. Ahuja and P. Jena, ChemPhysChem, 2012, 13, 300.
37. Q. L. Lu, J. W. Meng, W. J. Song and J. G. Wan, Int. J. Hydrogen Energy, 2013, 38, 13328.
38. S. Bandaru, N. J. English, A. D. Phillips and J. M. D. MacElroy, J. Comput. Chem., 2014, 35, 891.
39. M. S. Khan and M. S. Khan, Vacuum, 2014, 101, 151.
40. M. Samolia and T. J. D. Kumar, RSC Adv., 2014, 4, 30758.
41. J. L. Boone, J. Am. Chem. Soc., 1964, 86, 5036.
42. C. G. Zhang, R. Zhang, Z. X. Wang, Z. Zhou, S. B. Zhang and Z. Chen, Chem.–Eur. J., 2009, 15, 5910.
43. R. M. Kumar, J. V. Sundar and V. Subramanian, Int. J. Hydrogen Energy, 2012, 37, 16070.
44. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
45. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
46. A. D. Becke, J. Chem. Phys., 1997, 107, 8554.
47. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
48. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al., Gaussian 09. Revision D.01, Gaussian Inc, Wallingford CT, 2009.
50. S. S. Xantheas, J. Chem. Phys., 1994, 100, 7523.
51. S. S. Xantheas, J. Chem. Phys., 1995, 102, 4505.
52. A. Chaudhari, P. K. Sahu and S. L. Lee, J. Chem. Phys., 2004, 120, 170.
53. A. Chaudhari and S. L. Lee, J. Chem. Phys., 2004, 120, 7464.
54. P. Valiron and I. Mayer, Chem. Phys. Lett., 1997, 275, 46.
55. W. Zhou, T. Yildirim, E. Durgun and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085434.
56. D. R. Lide, CRC Handbook of Chemistry and Physics, New York, 75th edn, 1994.
57. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. WeinholdNBO Program, ver. 3.1, as implemented in link 607 of GAUSSIAN 09.

---