Effect of ionic strength on phosphorus sorption in different sediments from a eutrophic plateau lake

Abstract

The sorption of phosphorus under different ionic strengths was investigated in four types of sediment samples from the Chinese Dianchi Lake by kinetic and batch equilibrium experiments. The results showed that the sorption rate followed both the pseudo-first order and pseudo-second order. However, the pseudo-second order could better describe the sorption kinetics than the pseudo-first order. Sediments 1 (S1) and 4 (S4) had higher sorption capacities than Sediments 2 (S2) and 3 (S3). The sorption capacities of the four sediments were highly influenced by ionic strength, and low ionic strength was favorable for P uptake. The sorption kinetics of P to sediment was regulated by the surface-diffusion mechanism, and the diffusion rate of P from the liquid–sediment boundary to sediment surface determined its sorption rate. The classic Langmuir isotherm equation was modified to describe P sorption on sediments, and the modified Langmuir isotherm could describe the P sorption well. The native adsorbed phosphorus (NAP), equilibrium phosphorus concentration (EPC₀), and maximum phosphorus capacity (Q_m) varied with ionic strength. The Fe/Al oxide in the sediment had a significant relationship (R² > 0.95, P < 0.05) with NAP, EPC₀, and Q_m. The positions of S1 and S4 had the potential risk of P release, whereas S2 and S3 play a pool role of P.

---

1. Introduction

Phosphorus, as one of the main nutrients, is found in soils, sediments, water, and organisms.^1,2 However, excessive P can cause eutrophication and the chaotic growth of undesirable algae and other aquatic plants,^3,4 which has become a widespread environmental problem. P in sediment exists in different forms (e.g., calcium, iron, or aluminum complex salts and organic species), can be adsorbed onto the surface of minerals, and is an important part of many structural and biochemically functional components for cell growth of plants.^5,6 Lake sediments can act as either P sources or pools to the overlying water column. Therefore, understanding the transformation process of P at the sediment–water interface is increasingly becoming important.

In the past, P sorption characteristics on homogeneous sorbents such as goethite, which contain pure minerals,^7,8 has been described by different models that have been used to describe P sorption on sediments. For instance, simple Langmuir and Freundlich models were extensively used to describe the sorption features of P on sediments.^9,10 However, the sediment, which is different from homogeneous sorbents, has complex components. P exists in the sediment in various forms, such as Ca–P, Al–P, Fe–P, and organic P. The native adsorbed phosphorus (NAP) can immediately participate in the sorption or desorption process to influence the sorption or desorption capacity of the sediment. Researchers used oxalate-extractable phosphorus to represent NAP in sediments.^11,12 However, NAP content may change with sediment composition or environmental conditions such as lake chemistry.^6,13 Therefore, NAP cannot be neglected or replaced by oxalate-extractable P in the descriptive model for sorption or desorption processes.

Many experimental conditions that can influence the sorption process, such as pH and temperature, have been investigated. A previous study¹⁴ indicated that P sorption increased as the pH increased from pH 2 to pH 4 in Taihu Lake sediments (China). Detenbeck and Brezonik¹³ found that the sorption decreased when pH increased from pH 4 to pH 6 in Little Rock Lake (Wisconsin, USA). Furthermore, some studies indicated that P sorption increased with temperature increasing, thus decreasing the soluble P fraction.^15,16 These studies indicated that pH and temperature effects differ by sediment. The ionic strength effect has been explored in the area of organic matter (OM) sorption. Some researchers found that under high ionic strength conditions, the water solubility of OM adhered to soil particles decreased because of the salting-out effect.¹⁷ Moreover, the abundant cation in the liquid–solid system could interact with the negative charges of the solid surface. The abundant anion would compete on the active site during the anion sorption process. However, few studies focused on the effect of ionic strength on P sorption in the sediments. Research into P sorption has also been conducted in diverse sediment types. These studies have almost exclusively focused on sediments in shallow lakes, estuaries, or reservoirs,^18–20 whereas information about P sorption or desorption of sediments in plateau lakes are limited or nonexistent. Therefore, the effect of ionic strength on P in sediments should be emphasized. Dianchi Lake, a typical plateau lake, is located in southwestern China and was selected as the research area.

The objectives of the present study are mainly to describe the sorption kinetics of P onto sediments from Dianchi Lake and to model P sorption processes by modified isotherm. Meanwhile, the effect of ionic strength is evaluated. This study provides the useful information for sediment management.

2. Materials and methods

2.1 Area description

Dianchi Lake is a plateau lake (water surface elevation = 1886 m) located in southwestern China (24°48′N; 102°40′E). The lake covers an area of 330 km² with a volume of approximately 1.2 × 10¹¹ m³. The lake is divided into two sections. The northwestern part is called Caohai and the southern part is called Waihai.^21,22 These two sections are separated by Hubing Road (Fig. 1) with a sluice. This study area is located beside Hubing Road in Waihai and encloses two large enclosures (Fig. 1).

Fig. 1 Sampling site at the study area.

2.2 Sediment collection and characterization

Four composite surface sediment samples (each N = 7) were collected at the sites shown in Fig. 1 in April 2014. Sediment 1 (S1) was collected in a small enclosure and Sediment 2 (S2) was collected at the border of the enclosure. Sediments 3 (S3) and 4 (S4) were located between two large enclosures and in the deepest area, respectively. The sediment samples were immediately brought to the laboratory, where they were freeze-dried, ground, and sifted through 100 mesh (0.150 mm) sieve to obtain uniform size.²³ The total phosphorus (TP) of the sediments was measured by using the standard measurement and test (SMT).²⁴ In this procedure, HCl (3.5 mol L⁻¹) was used as extractants and an intake of 200 mg of sediment which was calcined at 450 °C for 3 hours was necessary for the extraction. Oxalate-extractable P (Ox-P) in sediment was measured using ammonium chloride (NH₄Cl) as extractants.²⁵ The P concentration in the solution was determined by the molybdenum blue method after the solution was filtered (0.45 μm filtration membrane).²⁶ The pH of the sediment was measured in a 1 : 2.5 (w/v) mixture of sediment with deionized water or 0.01 mol L⁻¹ KCl solution.²⁷ OM content was calculated according to the loss on ignition to constant mass (4 h) at 550 °C. The specific surface area was measured by the N₂ adsorption method with the surface analyzer (Micromeritics, USA) in the relative atmospheric pressure range of 0.001 to 0.995. The chemical composition of the samples was determined by X-ray fluorescence analyzer (S4 EXPLORER, Germany). The main properties of the collected sediments are shown in Table 1.

Table 1 Physicochemical properties (mean value ± standard deviation) of four sediments

Propert (unit)	S1	S2	S3	S4
TP (mg kg^−1)	1395.98 ± 60.48	1150.59 ± 58.45	996.87 ± 50.87	950.61 ± 55.89
TN (mg kg^−1)	2572.59 ± 75.69	3127.40 ± 73.38	3312.34 ± 69.35	1595.07 ± 54.84
Ox-P (mg kg^−1)	323.21 ± 26.21	265.33 ± 20.05	287.56 ± 21.45	345.12 ± 28.21
OM (%)	13.75 ± 0.24	10.88 ± 0.18	9.68 ± 0.16	12.89 ± 0.21
pH [H2O]	7.39 ± 0.07	7.93 ± 0.06	7.88 ± 0.10	7.28 ± 0.08
pH [KCl]	7.24 ± 0.06	7.79 ± 0.11	7.75 ± 0.08	7.11 ± 0.05
Fe oxide (%)	8.70 ± 0.07	6.56 ± 0.06	8.78 ± 0.09	8.43 ± 0.05
Ca oxide (%)	26.2 ± 0.4	15.9 ± 0.3	22.5 ± 0.4	26.5 ± 0.3
Al oxide (%)	16.6 ± 0.3	13.1 ± 0.3	11.8 ± 0.2	16.6 ± 0.2
Mg oxide (%)	2.14 ± 0.04	1.31 ± 0.03	1.5 ± 0.03	2.14 ± 0.02
BET surface area (m^2 g^−1)	10.44 ± 0.31	7.70 ± 0.28	4.56 ± 0.19	9.12 ± 0.25

---

2.3 Sorption kinetics study

P sorption kinetics was examined at 4 different ionic strengths of 0, 0.001, 0.01, and 0.1 M KCl. The stock solution, which was obtained by dissolving the salt KH₂PO₄ and KCl in deionized water, was prepared within 24 h before use and was stored in the dark at 4 °C until use. Four different sediments (1 g) were added to a series of 150 mL conical flasks containing 50 mL of 10 mg L⁻¹ P solution with different ionic strengths (viz. 0, 0.001, 0.01, and 0.1 M KCl). The sediment suspensions were immediately covered with parafilm and constantly agitated on a temperature-controlled shaker at 200 rpm under a constant temperature of 25 ± 2 °C. At 11 different time intervals (0.5, 1, 2, 4, 8, 12, 24, 36, 48, 60, and 72 h), the suspensions were taken from each flask, centrifuged, filtered (0.45 μm), and analyzed for P content. The experiments were conducted in triplicate, and the sediment sample (1 g) to solution (50 mL) ratio was assumed constant throughout the incubation period.

2.4 Sorption isotherm tests

The sorption isotherms of P by sediments were obtained by using batch experiments. The sediment samples of 1 g in triplicate were added to a series of 150 mL conical flasks containing 50 mL P solution at different initial P concentrations (0, 1, 5, 10, 15, and 20 mg L⁻¹ as KH₂PO₄). In this sorption isotherm tests, four different ionic strengths were studied by using 0, 0.001, 0.01, and 0.1 M KCl. The conical flasks were agitated on a temperature-controlled shaker at 200 rpm under a constant temperature of 25 ± 2 °C for 48 h equilibration period. The suspensions were centrifuged, filtered (0.45 μm), and analyzed for P.

2.5 Kinetic and equilibrium sorption data fitting

The P uptake amount onto the different sediments at each time, Q_t (mg g⁻¹), was calculated by using a mass balance relationship: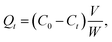where C₀ (mg L⁻¹) is the initial liquid-phase phosphorus concentration, C_t (mg L⁻¹) is the blank corrected concentration of P at time t, V (L) is the volume of the solution, and W (g) is the mass of dried sediment.

To investigate the mechanism of sorption and potential rate-controlling steps, pseudo-first and -second order models and Weber–Morris model were used to describe the sorption kinetics.^28,29

The pseudo-first order model is expressed as follows:

Q_t = Q_e(1 − e^−K₁t), (2)

where Q_t and Q_e are the uptake amounts (mg g⁻¹) of P adsorbed at time point t and equilibrium (mg g⁻¹), respectively. K₁ (h⁻¹) is the first-order kinetic rate constant and t is time (h).

The pseudo-second order model can be expressed as follows:

where K₂ is the sorption rate constant of the pseudo-second order kinetic model (g mg⁻¹ h⁻¹).

The Weber–Morris model is expressed as follows:

Q_t = K_at^0.5 + C, (4)

where C is the intercept of the vertical axis (mg g⁻¹) and K_a is the intra-particle diffusion rate constant for sorption (mg g⁻¹ h^−0.5).³⁰

Sorption isotherm data are also fitted by using Langmuir and Freundlich sorption models.

The Langmuir model is expressed as follows:

where Q_e and Q_m are the sorbed amount of P in the sediments at equilibrium and the maximum P uptake amount (mg g⁻¹), respectively. C_e is the P concentration in the aqueous phase at equilibrium (mg L⁻¹), and K is the affinity parameter (L mg⁻¹).

The Freundlich model is expressed as follows:

Q_e = K_fC_eⁿ, (6)

where K_f is the sorption coefficient (L g⁻¹) and n is a constant used to measure the sorption intensity or surface heterogeneity.³¹

When the sediment interacts with water, P will be exchanged between the water and sediment during the interface until a dynamic equilibrium is reached. The Langmuir sorption isotherm usually describes the equilibrium situation.⁶ Further studies indicated that the Langmuir model has been used widely to describe the anion sorption by soil and sediments^10,32 despite their heterogeneous nature. However, the Langmuir model could not work perfectly because of NAP in the sediment.³² Therefore, to study P sorption directly, eqn (5) is unreasonable because the NAP in the sediment is also included in the sorption equilibrium.³³ By considering NAP, the equilibrium conditions of sorption trials could be described as follows:

and the value of NAP can be calculated by eqn (8).⁶where C⁰_e and Q⁰_e is the equilibrium concentration (mg L⁻¹) and uptake amount (mg g⁻¹), respectively, whereas C_add (the initial concentration of newly added P in solution of sorption trials) is equal to 0 mg L⁻¹.

Thereafter, the modified Langmuir sorption isotherm can be expressed as follows:

P sorption properties on lake sediments that contain different amounts of NAP could be described by eqn (9). By using this model, the data of sorption isotherm trials could be nonlinearly fitted properly with the least square method. The value of Q_m and K were obtained. Thereafter, NAP could be calculated by eqn (8). The zero equilibrium phosphorus concentration (EPC₀) is the concentration in which no net sorption or desorption of P occurs, and the original sediment and water P concentrations are in dynamic equilibrium. When Q_e = 0 or C_add = C_e, the EPC₀ value (C_e) according to eqn (9) is expressed as follows:³⁴

The newly added P is assumed to directly compete with NAP and they have the same values of Q_m and K. K_p can be calculated as follows:

3. Results and discussion

3.1 P sorption kinetics

The sorption kinetic was most commonly described with the pseudo-first and pseudo-second order models.³⁵ Three steps are considered in kinetic models: (1) the sorbate ions diffuse from the liquid phase to the liquid–solid boundary; (2) the sorbate ions move from the liquid–solid boundary to the solid surface; (3) the sorbate ions diffuse into the particles.³⁶ The experimental results corresponding to the P sorption onto four sediments under study (Q_t versus t) together with fitting to the kinetic equations are shown in Fig. 2 and Table 2. The kinetic behavior of P sorption onto these four sediments was examined by 72 h contact time. In these figures, the P sorption from solution onto four sediments was relatively rapid in the first few hours (0 h to 8 h) and the sorption rate progressively diminished until an apparent equilibrium (8 h to 48 h) was reached. This result was similar to early published results on P sorption onto sediments.^37,38 In the first few hours, the active sorption sites were occupied rapidly. In the next few hours, the active sorption sites were reduced and the P sorption rate decreased. After 48 h, the sorption equilibrium could be achieved or desorption might occur for all sediments.

Fig. 2 Sorption kinetics of phosphorus on four sediments.

Table 2 Parameters for pseudo-first and pseudo-second order as well as Weber–Morris models

Sample	Ionic strength (M)	Pseudo-first order model			Pseudo-second order model			Weber–Morris model
		Qe (mg g^−1)	K1 (h^−1)	R^2	Qe (mg g^−1)	K2 (g mg^−1 h^−1)	R^2	C (mg g^−1)	Ka (mg g^−1 h^−0.5)	R^2
S1	0	0.396 ± 0.009	2.161 ± 0.350	0.9487	0.409 ± 0.005	9.681 ± 1.267	0.9881	0.309 ± 0.018	0.028 ± 0.007	0.8329
	0.001	0.406 ± 0.008	2.225 ± 0.338	0.9556	0.418 ± 0.004	10.095 ± 1.187	0.9908	0.324 ± 0.021	0.027 ± 0.008	0.7572
	0.01	0.402 ± 0.008	2.517 ± 0.388	0.9596	0.414 ± 0.004	11.915 ± 1.490	0.9911	0.324 ± 0.016	0.026 ± 0.006	0.8409
	0.1	0.330 ± 0.007	2.597 ± 0.438	0.9534	0.340 ± 0.004	14.973 ± 2.262	0.9874	0.263 ± 0.013	0.022 ± 0.005	0.8596
S2	0	0.299 ± 0.007	1.722 ± 0.256	0.9500	0.310 ± 0.003	9.583 ± 0.970	0.9912	0.222 ± 0.009	0.024 ± 0.004	0.9319
	0.001	0.302 ± 0.007	1.576 ± 0.230	0.9498	0.313 ± 0.003	8.624 ± 0.827	0.9916	0.218 ± 0.010	0.026 ± 0.004	0.9351
	0.01	0.295 ± 0.006	1.881 ± 0.269	0.9556	0.305 ± 0.003	11.221 ± 1.150	0.9918	0.226 ± 0.008	0.022 ± 0.003	0.9504
	0.1	0.226 ± 0.005	1.314 ± 0.187	0.9496	0.235 ± 0.003	9.224 ± 0.951	0.9893	0.167 ± 0.008	0.016 ± 0.003	0.9083
S3	0	0.366 ± 0.009	1.950 ± 0.339	0.9366	0.379 ± 0.005	9.124 ± 1.348	0.9831	0.260 ± 0.018	0.035 ± 0.007	0.8934
	0.001	0.372 ± 0.009	2.130 ± 0.384	0.9364	0.385 ± 0.006	9.708 ± 1.545	0.9815	0.270 ± 0.017	0.032 ± 0.006	0.8872
	0.01	0.373 ± 0.009	1.999 ± 0.340	0.9401	0.386 ± 0.005	9.186 ± 1.291	0.9850	0.283 ± 0.015	0.028 ± 0.006	0.8804
	0.1	0.300 ± 0.008	2.097 ± 0.406	0.9259	0.311 ± 0.005	12.020 ± 2.185	0.9760	0.226 ± 0.020	0.024 ± 0.007	0.7362
S4	0	0.429 ± 0.008	2.594 ± 0.370	0.9663	0.440 ± 0.004	11.846 ± 1.389	0.9926	0.352 ± 0.01	0.024 ± 0.004	0.9209
	0.001	0.425 ± 0.008	2.817 ± 0.450	0.9619	0.437 ± 0.005	13.294 ± 2.074	0.9883	0.361 ± 0.004	0.018 ± 0.002	0.9752
	0.01	0.421 ± 0.007	2.589 ± 0.357	0.9684	0.432 ± 0.004	12.211 ± 1.385	0.9931	0.354 ± 0.010	0.020 ± 0.004	0.8979
	0.1	0.381 ± 0.007	3.312 ± 0.585	0.9634	0.390 ± 0.005	18.721 ± 3.744	0.9854	0.330 ± 0.004	0.013 ± 0.001	0.9666

---

The rate constants and parameters of the pseudo-first and -second order models derived from the nonlinear regression (eqn (2) and (3)) are shown in Table 2. The kinetic sorption data of P by sediments were well fitted with the pseudo-second order model compared with the pseudo-first order model, as indicated by higher correlation coefficients (R² > 0.97). S1 and S4 had higher phosphorus uptake amounts at the equilibrium (Q_e) than S2 and S3 (Table 2). This result could be attributed to the relatively high Fe, Al, and Ca oxide contents among sediments to provide abundant specific areas (Table 1) for P sorption.¹² Regarding these four sediments, they displayed different P sorption kinetic constants, and the K₂ values were S4 > S1 > S3 > S2 in the same ionic strength. The comparison of the kinetic constants obtained for sediments with the physicochemical characterization (Table 1) showed that S1 and S4 had relatively high OM, Fe, Al, and Ca oxides. A previous study³⁹ indicated that sorption velocity was favored by the OM content of the samples. Therefore, S1 and S4 displayed not only the largest Q_e but also the largest K₂ and Fe. Al and Ca oxides favored both the uptake amount and velocity of P sorption; this result is consistent with literature.^40,41 Regarding the pH measured in either in H₂O or in KCl, the P uptake amount and K₂ values were enhanced by relatively low pH values because the increase in pH might prevent P sorption onto Fe, Al, and Ca oxides according to the speciation shifting of phosphate from H₂PO₄⁻ to HPO₄²⁻; the surface charges of Fe, Al, and Ca oxides were also modified.^42,43 The kinetic sorption data showed that P sorption onto S1 and S4 occurred rapidly compared with S2 and S3.

However, the diffusion process of P in pores or that from the liquid–sediment boundary to sediment surfaces was inconclusive. To reveal the relative contribution of surface and intra-particle diffusion to the entire sorption process, the kinetic sorption data of P in the sediment were further fitted with the Weber–Morris model. The sorption process could be divided into three steps: a sharp rise portion, a less-sharp rise portion, and a plateau (Fig. 3). In the first step, approximately 40.0% to 73.1% of P was sorbed into the sediment because of the occupation of exterior activated site by various physicochemical interactions, such as covalent forces, hydrophobic interaction, and van der Waals forces. Furthermore, the thickness of the boundary layer (C) for S1 and S4 (Table 2) was relatively larger compared with S2 and S3.⁴⁴ The surface sorption played a significant role for P in the sediment. In the second step, approximately 16.4% to 19.6% of the P that sorbed into the sediment was slowly diffused from the liquid–sediment boundary to the sediment surfaces. In the third step, the P sorption approached equilibrium and desorption processes might occur. By contrast, if the regression of Q_t against t^1/2 was linear and the regression line passed through the origin, then the intra-particle diffusion was presumed to be the rate-controlling step.³⁶ The Weber–Morris models results in Table 2 and Fig. 3 revealed that Q_t was linearly correlated with t^1/2 and that all regression lines did not pass through the origin with positive intercepts, thus suggesting that the diffusion on the pores might not be a rate-controlling step for the kinetic sorption of P to sediment. Therefore, the sorption kinetic of P to sediment was regulated by the surface-diffusion mechanism and the diffusion rate of phosphorus from the liquid–sediment boundary to the sediment surface determined their sorption rate.

Fig. 3 Weber–Morris model plot of phosphorus on four sediments.

3.2 Ionic strength effects on P sorption

The effect of ionic strength (with KCl as background electrolyte) on P sorption by four sediments was investigated by using batch methods. P uptake amount was statistically insignificant in the 0, 0.001, and 0.01 M KCl treatments and in the 0.001 M KCl solution (Fig. 2); the sediment had relatively high sorption capacity. When the ionic strength increased from 0 M KCl to 0.01 M KCl, the introduction of cations (K⁺) would make the plane potential less negative to increase the electrostatic potential (ψ), thereby facilitating P uptake capacity.⁴⁵ Although chloride ions with low ionic strengths (0, 0.001, and 0.01 M) would compete with P ions on the active sites, the high values of the water-soluble P and ion concentrations in the solution might not cause a noticeable variation in P uptake amount. As the ionic strength increased from 0.01 M KCl to 0.1 M KCl, the P uptake amount considerably decreased. Previous studies^46,47 suggested that the ion exchange reaction was the mechanism for adverse anion effects on P sorption. The introduction of competing anions would reduce the uptake amount of P. The chloride ions would compete with phosphate ions on the active site to replace the pre-adsorbed phosphate.

3.3 Equilibrium sorption of P

The effects of ionic strength on the equilibrium sorption isotherm of P were studied, and Fig. 4 shows the results. The P uptake amounts were S4 > S1 > S3 > S2 in 0, 0.001, 0.01, and 0.1 M ionic strength. P uptake amount was statistically insignificant in the 0, 0.001, and 0.01 M KCl treatments, and in the 0.1 M KCl solution, the P uptake amount was relatively low. The P uptake amount also increased with increasing P initial concentration, and the increase rate decreased as the equilibrium concentration increased in 0, 0.001, and 0.01 M KCl treatments (Fig. 4a–c). However, when the ionic strength increased to 0.1 M, the increased rate of P uptake amount became unstable (Fig. 4d). This result might be explained on the basis of the ion exchange mechanism that played an important role in the sorption process, and the chloride ions would compete with phosphate ions on the active sites.

Fig. 4 Sorption isotherms of phosphorus on four sediments.

The fitting of sorption isotherm equations to experimental sorption is usually a significant aspect of understand sorption behavior. In this study, the sorption isotherms of P by four sediments are presented in Fig. 4, and the isotherm data were fitted with the modified Langmuir and Freundlich models (Table 3). As evidenced by the correlation coefficient R², the P sorption isotherm of four sediments can be described by using the modified Langmuir model (R² > 0.9885) rather than using the Freundlich model (R² < 0.9806). The Langmuir sorption isotherm provided a good estimate of the theoretical sorption maxima (Q_m), thus reflecting the sorption capacity of sorbent and the affinity parameter K. The values of Q_m and K in this study were obtained in Table 3, and the Langmuir sorption maxima and the affinity parameter of these four sediments ranged from 0.527 mg g⁻¹ to 1.126 mg g⁻¹ and 0.252 mg g⁻¹ to 0.983 L mg⁻¹ in different ionic strengths, respectively. The change in Q_m and K was statistically insignificant to the change in ionic strength from 0 M to 0.01 M because the introduction of cations (K⁺) would increase the electrostatic potential (ψ) to facilitate the P uptake capacity or a small amount of chloride ions would compete with phosphate ions on the active site to decrease the P uptake amount. However, when the KCl concentration increased from 0.01 M to 0.1 M, the ionic strength reached a certain level in which the background electrolyte (KCl) not only reduced the uptake amount but also reduced the binding affinity of the absorbent. The introduction of chloride ions would change the sorption atmosphere of the sorbent surface. Therefore, when the KCl concentration increased to 0.1 M, chloride ions competed on the active sites with phosphate ions, and the atmosphere of the sorbent surface could be modified.

Table 3 Langmuir and Freundlich models parameters for sorption of phosphorus

Sediment sample	Ionic strength (M)	C^0e (mg L^−1)	Q^0e (mg g^−1)	Langmuir:						Freundlich: Qe = KfCe^n
				Fitting results			Calculated results			Fitting results
				K (L mg^−1)	Qm (mg g^−1)	R^2	EPC0 (mg L^−1)	NAP (mg g^−1)	Kp (L g^−1)	Kf (L g^−1)	n	R^2
#1	0	0.072	0.0036	0.734	0.970	0.9993	0.065	0.052	0.800	0.307	0.543	0.9413
	0.001	0.061	0.0031	0.606	1.056	0.9998	0.069	0.041	0.597	0.307	0.573	0.9611
	0.01	0.072	0.0036	0.669	0.980	0.9984	0.068	0.049	0.718	0.304	0.548	0.9559
	0.1	0.146	0.0073	0.562	0.923	0.9931	0.116	0.077	0.665	0.269	0.552	0.9386
#2	0	0.093	0.0047	0.380	0.604	0.9949	0.039	0.025	0.657	0.146	0.512	0.9567
	0.001	0.072	0.0036	0.456	0.650	0.9894	0.033	0.024	0.729	0.132	0.546	0.9806
	0.01	0.061	0.0031	0.348	0.591	0.9971	0.026	0.015	0.605	0.148	0.492	0.9592
	0.1	0.188	0.0094	0.252	0.527	0.9911	0.065	0.033	0.510	0.107	0.548	0.9458
#3	0	0.072	0.0036	0.594	0.742	0.9957	0.041	0.034	0.839	0.219	0.503	0.9566
	0.001	0.051	0.0025	0.701	0.718	0.9885	0.027	0.027	1.015	0.240	0.457	0.9248
	0.01	0.083	0.0041	0.617	0.734	0.9951	0.045	0.040	0.889	0.221	0.485	0.9387
	0.1	0.157	0.0078	0.438	0.702	0.9956	0.078	0.053	0.675	0.150	0.604	0.9611
#4	0	0.061	0.0031	0.802	1.091	0.9992	0.070	0.054	0.774	0.372	0.565	0.9492
	0.001	0.051	0.0025	0.983	1.053	0.9940	0.054	0.053	0.983	0.395	0.543	0.9344
	0.01	0.051	0.0025	0.632	1.126	0.9991	0.065	0.038	0.581	0.358	0.577	0.9677
	0.1	0.104	0.0052	0.637	1.025	0.9902	0.103	0.069	0.666	0.280	0.585	0.9317

---

Theoretically, EPC₀ and NAP have the same values for the same sediment. Some studies^12,48 and even recent research¹¹ on the effect of different conditions on P sorption to sediments used oxalate-extractable P to represent NAP in sediments. However, in the current study, the same sediment had different EPC₀ and NAP values (Table 3) in different ionic strengths, and the NAP values varied greatly with changing ionic strength, thus indicating that the NAP value would vary with experimental conditions, such as ionic strength, temperature, and pH. Furthermore, the oxalate-extractable P could not represent NAP. The sorption behavior of the same sediment was studied in different experimental conditions. The NAP of different sediments in different ionic strengths was obtained. S1 and S4 had relatively higher NAP (0.038 mg g⁻¹ to 0.077 mg g⁻¹) compared with S2 and S3 (0.015 mg g⁻¹ to 0.053 mg g⁻¹) (Table 3). For the same sediment in Table 3, as ionic strength ranging from 0 M to 0.01 M, NAP had a slight change. When the ionic strength increased to 0.1 M, the NAP reached a high value. In addition, the K_p value reflects the relative affinities of the solid phase for P. The large value of K_p indicated the high ability of P sorption. Table 3 indicated that S1 and S4 have the better P sorption capacity than S2 and S3 according to K_p value. Researchers have concluded that sediment composition significantly influenced NAP, EPC₀, and Q_m values. The inter-correlations among NAP, EPC₀, Q_m, Ca oxide, and Fe/Al oxide are shown in Table 4. The Fe/Al oxides in sediment have significant relationships (R² > 0.95, P < 0.05) with NAP, EPC₀, and Q_m. The relationship between NAP and Ca oxide was also significant. This relation demonstrated that Fe/Al and Ca oxides played major roles in P sorption. The metal hydroxides of Fe, Al, and Ca are widely known to be the main absorbents for P. Therefore, the high content of Fe, Al, and Ca oxides in S1 and S4 caused the high P sorption capacity.

Table 4 Pearson correlation coefficients between native adsorbed phosphorus (NAP), zero equilibrium phosphorus concentration (EPC₀), the maximum phosphorus uptake amount (Q_m), Fe/Al oxide and Ca oxide^a

	NAP	EPC0	Qm	Fe/Al oxide	Ca oxide
a *P < 0.05.
NAP	1
EPC0	0.975*	1
Qm	0.986*	0.973*	1
Fe/Al oxide	0.986*	0.983*	0.956*	1
Ca oxide	0.951*	0.860	0.933	0.899	1

---

3.4 The dual nature of sediments as a pool and source of P in the study area

Depending on the dynamic equilibrium between solution and solid phases, P can either be adsorbed or desorbed from sediments. The determination of sediment EPC₀ value can reveal the direction of soluble reactive phosphorus (SRP) flux.⁴⁹ If EPC₀ is greater than the SRP concentration in pore water, then the sediment will release P and vice versa. In the present study, the sorption isotherms produce EPC₀. The SRP concentrations in pore water (C_pwp) and overlying water (C_owp) are shown in Table 5. When C_pwp = EPC₀, P sorbed = 0 (neither pool nor source); when C_pwp > EPC₀, P sorbed > 0 (sediment serves as pool of phosphorus); when C_pwp < EPC₀, P sorbed < 0 (sediment serves as source of phosphorus).⁶ For S1 and S4, the values of C_pwp were smaller than EPC₀, and these two sediments were sources of P. Furthermore, in the study area, the ionic strength in overlying water ranges from 10⁻³ mg L⁻¹ to 10⁻² mg L⁻¹, and the average value of sediment cation exchange capacity (CEC) is approximately 0.25 mol (+) kg⁻¹. The differences of ionic strength may cause the change of EPC₀, which is one of the main reasons for sediment serving as source or pool of phosphorus. Therefore, this finding explained why SRP concentrations in the overlying water (C_owp) of these two points were higher than the other two points. For S2 and S3, the values of C_pwp were larger than EPC₀, and these two sediments have a pool role of P, thus resulting in lower C_owp than that in S1 and S4.

Table 5 Zero equilibrium phosphorus concentration (EPC₀) and soluble reactive phosphorus (SRP) concentration in pore water (C_pwp) and overlying water (C_owp) of the study area

Sediment sample	EPC0 (mg L^−1)	Cpwp (mg L^−1)	Cowp (mg L^−1)
#1	0.065 ± 0.013	0.032 ± 0.009	0.022 ± 0.002
#2	0.039 ± 0.014	0.053 ± 0.011	0.015 ± 0.003
#3	0.041 ± 0.016	0.049 ± 0.012	0.017 ± 0.002
#4	0.070 ± 0.014	0.015 ± 0.008	0.029 ± 0.004

---

4. Conclusion

The study of P sorption kinetics is a valuable tool for evaluating the system response to P external loadings. The sorption rate followed both the pseudo-first order and pseudo-second order. The results showed that the pseudo-second order could better describe the sorption kinetics than the pseudo-first order. The sorption capacities of four sediments were S4 > S1 > S3 > S2 and was highly influenced by ionic strength. Low ionic strength was favorable for P uptake. By contrast, the sorption kinetic of P to sediment was regulated by the surface-diffusion mechanism, and the diffusion rate of P from the liquid–sediment boundary to the sediment surface determines their sorption rate. The modified Langmuir isotherm equation interprets well the P sorption data of these four sediments. The Fe/Al oxide in sediment has a significant relationship (R² > 0.95, P < 0.05) with NAP, EPC₀, and Q_m. Comparing the EPC₀ and C_pwp values, S1 and S4 are P sources, whereas S2 and S3 have pool role, providing useful information for sediment management.

Acknowledgements

This study was supported by the Major Science and Technology Program for Water Pollution Control and Treatment (No. 2012ZX07102-004).

References

1. X. L. Huang and J. Z. Zhang, Chemosphere, 2011, 85, 1227–1232.
2. V. Baldy, M. Trémolières, M. Andrieu and J. Belliard, Hydrobiologia, 2006, 575, 343–351.
3. L. E. de-Bashan and Y. Bashan, Water Res., 2004, 38, 4222–4246.
4. C. Yan, L. Zhang, X. Luo and Z. Zheng, Ecol. Eng., 2013, 51, 24–32.
5. R. A. Dorich, D. W. Nelson and L. E. Sommers, Agric., Ecosyst. Environ., 1984, 11, 253–264.
6. A. Zhou, H. Tang and D. Wang, Water Res., 2005, 39, 1245–1254.
7. T. Hiemstra and W. H. van Riemsdijk, J. Colloid Interface Sci., 1996, 179, 488–508.
8. J. S. Geelhoed, T. Hiemstra and W. H. van Riemsdijk, Environ. Sci. Technol., 1998, 32, 2119–2123.
9. P. Lopez, X. Lluch, M. Vidal and J. A. Morgui, Estuarine, Coastal Shelf Sci., 1996, 42, 185–196.
10. M. Del Bubba, C. A. Arias and H. Brix, Water Res., 2003, 37, 3390–3400.
11. L. Huang, L. Fu, C. Jin, G. Gielen, X. Lin, H. Wang and Y. Zhang, Ecol. Eng., 2011, 37, 1515–1522.
12. D. Y. F. Lai and K. C. Lam, Ecol. Eng., 2009, 35, 735–743.
13. N. E. Detenbeck and P. L. Brezonik, Environ. Sci. Technol., 1991, 25, 395–403.
14. S. R. Wang, X. C. Jin, Y. Pang, H. C. Zhao and X. N. Zhou, J. Colloid Interface Sci., 2005, 285, 448–457.
15. R. N. Sah and D. S. Mikkelsen, Plant Soil, 1986, 95, 173–181.
16. N. J. Barrow, J. Soil Sci., 1979, 30, 271–297.
17. A. Turner and M. C. Rawling, Water Res., 2001, 35, 4379–4389.
18. S. Leston, A. I. Lillebo and M. A. Pardal, Estuarine, Coastal Shelf Sci., 2008, 77, 688–696.
19. X. Y. Wang, L. P. Zhang, H. Zhang, X. Y. Wu and D. L. Mei, Environ. Earth Sci., 2012, 67, 15–22.
20. Q. R. Wang and Y. C. Li, J. Soils Sediments, 2010, 10, 1159–1173.
21. X. Qu, L. Xie, Y. Lin, Y. Bai, Y. Zhu, F. Xie, J. P. Giesy and F. Wu, Environ. Sci. Pollut. Res., 2013, 20, 7413–7423.
22. C. Huang, X. Wang, H. Yang, Y. Li, Y. Wang, X. Chen and L. Xu, Sci. Total Environ., 2014, 485–486, 1–11.
23. X. Jin, S. Wang, Y. Pang, H. Zhao and X. Zhou, Colloids Surf., A, 2005, 254, 241–248.
24. V. Ruban, J. F. Lopez-Sanchez, P. Pardo, G. Rauret, H. Muntau and P. Quevauviller, J. Environ. Monit., 2001, 3, 121–125.
25. L. Huang, L. Li, L. Huang, G. Gielen, Y. Zhang and H. Wang, J. Soils Sediments, 2011, 12, 443–455.
26. J. Murphy and J. P. Riley, Anal. Chim. Acta, 1962, 27, 31–36.
27. X. Liao, C. Zhang, L. Yao, J. Li, M. Liu, L. Xu and M. Evalde, Sci. Total Environ., 2014, 473–474, 530–536.
28. Y. S. Ho, D. A. J. Wase and C. F. Forster, Environ. Technol., 1996, 17, 71–77.
29. Y. S. Ho and G. McKay, Process Biochem., 1999, 34, 451–465.
30. W. J. Weber and J. C. Morris, ASCE J. Sanit. Eng. Div., 1963, 89, 31–59.
31. C. Sairam Sundaram, N. Viswanathan and S. Meenakshi, Bioresour. Technol., 2008, 99, 8226–8230.
32. W. A. House and F. H. Denison, Water Res., 2000, 34, 1187–1200.
33. A. Aminot and F. Andrieux, Water Res., 1996, 30, 2805–2811.
34. X. Wang, L. Zhang, H. Zhang, X. Wu and D. Mei, Environ. Earth Sci., 2011, 67, 15–22.
35. P. Janoš, P. Michálek and L. Turek, Dyes Pigm., 2007, 74, 363–370.
36. X. Wang, L. Shu, Y. Wang, B. Xu, Y. Bai, S. Tao and B. Xing, Environ. Sci. Technol., 2011, 45, 9276–9283.
37. M. Otero, J. P. Coelho, E. T. Rodrigues, M. A. Pardal, E. B. Santos, V. I. Esteves and A. I. Lillebo, Mar. Pollut. Bull., 2013, 77, 361–366.
38. O. Eljamal, J. Okawauchi, K. Hiramatsu and M. Harada, Environ. Earth Sci., 2012, 68, 859–863.
39. P. J. A. Howard and D. M. Howard, Biol. Fertil. Soils, 1990, 9, 306–310.
40. M. B. McGechan, Biosystems Eng., 2002, 82, 115–130.
41. H. K. Pant and K. R. Reddy, J. Environ. Qual., 2001, 30, 1474–1480.
42. M. E. Lebo, Mar. Chem., 1991, 34, 225–246.
43. J. J. G. Zwolsman, Estuarine, Coastal Shelf Sci., 1994, 39, 227–248.
44. X. P. Liao, C. X. Zhang, L. L. Yao, J. L. Li, M. Liu, L. Xu and M. Evalde, Sci. Total Environ., 2014, 473, 530–536.
45. N. S. Bolan, J. K. Syers and R. W. Tillman, J. Soil Sci., 1986, 37, 379–388.
46. L. Huang, W. Qiu, X. Xu and Y. Zhang, Chem. Ecol., 2013, 29, 519–528.
47. J. Liu, L. Wan, L. Zhang and Q. Zhou, J. Colloid Interface Sci., 2011, 364, 490–496.
48. D. Freese, S. Vanderzee and W. H. Vanriemsdijk, J. Soil Sci., 1992, 43, 729–738.
49. W. A. House and F. H. Denison, Environ. Sci. Technol., 2002, 36, 4295–4301.

---