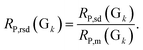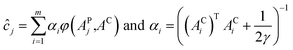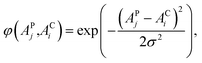Investigation of sample partitioning in quantitative near-infrared analysis of soil organic carbon based on parametric LS-SVR modeling

Abstract

Soil organic carbon (SOC) can be quantitatively determined with the enhanced stability of near-infrared (NIR) measurements. NIR analysis requires a modeling-validation division for real samples. The research of modeling robustness should be discussed in the modeling process based on an investigation of the calibration–prediction sample partitioning. A framework for sample partitioning is proposed with the consideration of the tunable ratio of numbers of the calibration and prediction samples. We addressed this issue in the multivariate calibration for NIR analysis of SOC using the least squares support vector machine regression (LS-SVR) method with an interactive grid search of its two modeling parameters, γ and σ, where γ is the regularization parameter directly influencing the Lagrange multiplier in the kernel transformation, and σ² represents the kernel width used to tune the degree of generalization. We created 7 volunteer groups for different ratios of calibration–prediction partitions. The calibration and prediction samples were re-produced for each volunteer group. The LS-SVR models were established and the parameters were optimally selected by considering the stability and robustness based on the statistical theory of mean value and relative standard deviation. Furthermore, in all comparative partition ratios, the optimal volunteer group was selected with the partition of 65 calibration samples and 35 prediction samples. Consequently, the optimized calibration model with correspondent optimal volunteer group was evaluated by the independent validation samples. The optimal LS-SVR parameters (γ, σ) were (110, 7), and the validation results revealed a root mean square error of 0.302 and a correlation coefficient of 0.907. This validation effect was considerably satisfactory for the random validation samples because an optimal volunteer group was chosen for calibration–prediction partition to guarantee the modeling stability and robustness in the process of model optimization.

---

1. Introduction

Near-infrared (NIR) spectroscopy is a rapid and reagent-less physical technique, requiring minimal or no sample preparation, and in contrast to traditional chemical analysis, it does not produce waste.^1,2 This technology has been widely used in many industries, including agriculture, environment, food processing, pharmaceuticals, and biomedicine.^3–6 NIR spectrometry permits a prediction of many soil properties from measurements. It has become popular in field measurement for the in situ prediction of various soil properties.^7–9 In particular, the diffuse reflectance of NIR spectroscopy is sensitive to the composition of organic carbon in soil.^10–12 Soil organic carbon (SOC) is an important component in agro-ecological soil. It represents a key parameter in evaluating the fertility of soils. SOC can be commonly and successfully predicted by NIR diffuse reflectance spectroscopy under laboratory-controlled conditions.^13,14

The use of NIR spectroscopy for the prediction of soil organic carbon (SOC) content in the field is highly desirable for soil quality assessment and carbon accounting purposes.^15–17 It has been demonstrated that SOC can be measured in the field with enhanced measurement stability at the expense of a slight decrease in accuracy compared to laboratory experiments.^18–20 Once the spectra have been calibrated for SOC, the chemometric methods can provide a rapid and inexpensive estimation of SOC in the field.

NIR analysis of SOC requires a modeling-validation division for real samples. Validation samples are utilized for model evaluation, and the strategy of modeling optimization should be discussed based on a calibration–prediction sample partitioning.^21,22 In multivariate calibration problems involving complex analytes, it is difficult to reproduce the composition variability of the samples using optimized experimental designs.²³ For the procedure of calibration–prediction modeling, the differences in the partitioning of calibration and prediction sets will lead to fluctuations in modeling parameters and thus yield unstable results. In particular, changes in the number of real samples in calibration set and prediction set will influence the robustness of the calibration models; thus, the prediction results will be unstable and the modeling optimization is difficult to achieve. In such cases, a representative calibration set is intensively desired, which must be extracted from the sample pool by considering the randomness, similarity and stability of calibration–prediction sample partitioning. This refers not only to the samples, but also to the partitioning ratio. Therefore, a tunable ratio of sample numbers for the partitioning of calibration and prediction sets is an important research topic.

Multivariate techniques take the spectrum into account and exploit the multi-channel nature of spectroscopic data to provide the signals of organic carbon from the spectral response of soil. Extraction of quantitative information requires the use of a reliable multivariate calibration method.^24,25 Linear regression methods (e.g. principal component regression, PCR, and partial least-squares, and PLS) show their ability to output promising results in specific applications.^26,27 However, agricultural translation of the effective chemometrics in NIR analysis has been largely impeded by the variations in the measurement.^28,29 Linear approaches cannot meet the quantitative modeling accuracy because the spectroscopic analysis of a single component in complex systems (such as soil) is influenced by the responses of other components and noises. Several investigators have recently employed least squares support vector machine regression (LS-SVR) as a nonlinear multivariate method that can handle ill-posed problems and lead to unique global models.^30–32 Several studies have addressed the issue of improvement in the prediction (or classification) accuracy arising from the use of LS-SVR in relation to conventional linear methods.

In this study, we emphasize the investigation of calibration–prediction sample partitioning in the NIR analysis of SOC with multivariate chemometrics. A framework for calibration–prediction partitioning is proposed with a consideration of the tunable ratio of numbers of calibration and prediction samples. First of all, a fixed-number portion of samples is randomly selected as the independent validation set, which should not be subjected to a modeling process. The remaining samples with a dependently fixed number were used for the process of modeling optimization. It is worth noting that the stable and robust calibration model depends on the partitioning ratio of the modeling samples divided into calibration and prediction sets by considering the randomness, similarity and robustness of the framework. We addressed this issue in the multivariate calibration problem involving NIR spectrometric analysis of organic carbon in soil. For example, the total number of modeling samples was fixed because, as abovementioned, the number of the independent validation samples is first identified. Therefore, the number of samples in the calibration and the prediction sets can be changed when the tunable partitioning ratio varies. A group of calibration and prediction sets corresponding to an unchanged partitioning ratio is marked as a volunteer group. The study involved a comparison of the different volunteer groups of calibration and prediction samples. The models obtained in this manner can be compared in terms of their modeling performance. In each volunteer group, the calibration–prediction partitions can be performed many times with a random selection of calibration samples. Based on the varied calibration–prediction partitions, the LS-SVR models can be parametrically optimized by considering the stability and robustness based on the fundamental statistical theory of the mean value and standard deviation. Furthermore, the optimal volunteer group can be chosen in all comparative partition ratios. Consequently, the optimized calibration model with correspondent optimal volunteer group can be estimated and evaluated by the samples in the independent validation set.

2. Theories and algorithms

2.1 Framework of sample partitioning and model optimization

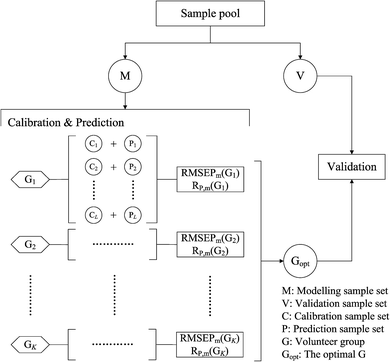
A framework for sample partitioning is proposed to take into account the tunable ratio of numbers of calibration and prediction samples, considering the randomness, stability and robustness of calibration models.

The algorithmic flowchart of this framework is shown in Fig. 1. As can be seen in Fig. 1, in the modeling-validation procedure, a fixed-number portion of validation samples (V set) is first extracted from the initial sample pool of the experimental data, before calibration–prediction partitioning. For the purpose of ensuring independence, the validation samples are randomly selected and totally not subjected to the modeling process. The remaining samples (M set) with a determined number are then partitioned into a calibration set and prediction set, and used further for the model establishment and parameter optimization. It is worth noting that the change in the numbers of calibration samples will result in modeling differences to affect the validating effects, thus a discussion of the partitioning ratio for calibration and prediction samples is necessary when considering the stability and robustness of this framework. For illustration, a fixed partitioning ratio will generate a pair of calibration and prediction sets, which are marked as a volunteer data group (G sets). We try to change the partitioning ratio of the calibration–prediction samples and perform model establishment and parametric optimization processes for each volunteer group (G₁, G₂… G_K). By comparing the modeling results, we can find out an optimized volunteer group (G_opt) to guarantee the stability and robustness of the models.

Fig. 1 Algorithmic flow chart for the framework of the sample partitioning and model optimization.

The calibration–prediction process was carried out for each volunteer group (G_k, k = 1, 2… K). We noted that the volunteer data groups (G sets) are only related to a fixed partitioning ratio, which means that one volunteer group only determines how many samples are used for calibration and how many are for prediction. There is still another issue for sample partitioning in each specific volunteer group: which sample for calibration can provide an improved modeling result? Several sets of experimental evidence indicate that differences in the sample partitioning of calibration and prediction sets will lead to fluctuations in the predictive parameters and yield unstable results.^33–35 On the level of stability and robustness, this issue requires this partitioning to be carried out randomly many times,^36,37 resulting in many different pairs of calibration sets and prediction sets (C_l + P_l, l = 1, 2… L). For the varied partitions of the calibration and prediction sets, the analytical models are established and the parameters are optimized by considering the modeling stability and robustness based on the mean value and standard deviation of the model indicators. For illustration, the root mean square error of the prediction (RMSEP) and correlation coefficients of prediction (R_P) are taken as two important indicators for the models. In one specific volunteer group (G_k), the modeling results for the pair of C_l + P_l are evaluated by RMSEP(l) and R_P(l). Going through all pairs of partitions in the fixed G_k, we have one RMSEP value and one R_P value for each pair of C + P. Based on all partitions in G_k, the mean value and standard deviation of all RMSEPs and R_Ps are calculated and denoted as RMSEP_m(G_k), R_P,m(G_k), RMSEP_sd(G_k) and R_P,sd(G_k). For statistical reasons, the relative standard deviation (RSD) was proposed to evaluate the actual frustration accompanied with the mean values. The RSD values of RMSEP and R_P could be calculated and denoted as

The RMSEP_m(G_k) and R_P,m(G_k) are used for evaluating the prediction accuracy of G_k, and the RMSEP_rsd(G_k) and R_P,rsd(G_k) are for the modeling stability. According to this strategy, we can calculate RMSEP_m and R_P,m for each volunteer group (G_k, k = 1, 2… K). All of the RMSEP (or R_P) values of each volunteer group will be located in the designated numerical region of RMSEP_m × (1 ± RMSEP_rsd) (or R_P,m × (1 ± R_P,rsd)). We have the knowledge that a lower RMSEP_m (or alternatively a higher R_P,m) indicates higher accuracy for the model and a lower RMSEP_rsd and R_P,rsd reflect higher modeling stability. Therefore, by comparing the values of RMSEP_m and R_P,m, we can select the optimal volunteer group (denoted as G_opt), which are expected to give a prospective promising result if utilized in a validation process.

2.2 The theory of LS-SVR

LS-SVR algorithm employs a set of linear equations to reduce the complexity of optimization process associated with the SVR methodology.³⁸ For the NIR spectral data, the predictive concentration ĉ_j of the j-th prediction sample is expressed in the following manner:
where α_i is the Lagrange multiplier that depends on the regularization parameter, γ,³² φ(x_j,x_i) is the kernel function, A^P_j is the NIR spectrum of the j-th sample in the prediction set, and A^C is a linear combination of all the calibration spectra (the NIR spectra with m wavenumbers), weighted by the concentration values.

The distribution of the feature samples in high dimensional space depends on the selection of the kernel and corresponding parameters. The Gaussian radial basis function (RBF) kernel has moderate robustness and stability to enable nonlinear modeling for the acquired NIR dataset, and it is expressed as follows:

where σ² represents the kernel width and is used to tune the degree of generalization. When RBF is selected as the kernel, the performance of LS-SVR depends primarily on the selection of the parameters, γ and σ². The regularization parameter γ determines the trade-off between the training error (which can be thought of as the model accuracy in the calibration dataset) and the model robustness. To optimize these two parameters, we proposed a multi-scale interactive grid search to enable the development of suitable calibration models. Careful selection of γ and σ² is necessary to search for a smooth subarea to obtain a low prediction error.

3. Samples and data

One hundred and thirty-five soil samples were collected from three farmlands in Guangxi (one autonomous region, China). In all the cases, the soils were under pure wheat or white rice or associated with other species such as sweet potato. Approximately 10% of samples were red soils and the rest of samples were the common yellow soils. The 135 sites were located depending on the area of each farmland. Based on the principle of homogeneous distribution, we chose 38, 45, and 52 sites from small, medium and large farmland, respectively. The distances between each adjacent site were slightly different, ranging about 3 to 5 meters. At each site, 10–15 cores were extracted from 0–15 cm in depth. Each core weighed about 2 grams and these cores were mixed together to comprise a sample. All the samples were numbered successively from 1 to 135. The samples were first dried and finely ground in the laboratory, and then passed through a 0.5 mm soil sifter to ensure that the samples were refined to an average of small-size solid particles. Two equivalent sets weighing 10 grams were then extracted from each sample, with one set for the biochemical measurement and the other for spectroscopic detection. The SOC content of each sample was measured using the routine biochemical method of potassium dichromate oxidation.³⁹ The measured values of all the samples, statistically, ranged from 1.10 to 6.42 (%), with an averaging value of 2.686 (%) and a standard deviation of 1.056 (%). These laboratorial values were used for spectroscopic analysis with an investigation of the calibration–prediction–validation sample divisions.

The measurement of spectral data was performed using a Spectrum One NTS FT-NIR spectrometer (PerkinElmer Inc., USA). The inner part of a spectrometer is the optical system composed of several devices. NIR light is produced by a built-in tungsten halogen light source, going through a light-splitting unit; thus, the light is split into a series of point lights, corresponding to each NIR wavelength. Then, every point light one-by-one goes through the sample filled in a round sample cell. This is the key process of spectral scanning. In the sample cell, the light is absorbed and reflected by the sample particles and the out-coming light intensity becomes weakened. A diffuse reflectance accessory is equipped here to amplify the out-coming light. A pair of InGaAs detectors is monitoring the original and the weakened light information. A signal of the NIR spectrum responses is generated using the amplified original and weakened light information. Consequently, the spectrum goes through a Fourier transform amplitude analyzer and the signals are delivered to a computer for digital analysis.

The whole spectroscopic measurement should be conditioned throughout the spectral scanning process. The temperature was controlled at 25 ± 1 °C and the relative humidity was limited at the spot of 46% ± 1% RH. The scanning range of the spectrum spanned from 10 000 cm⁻¹ to 4000 cm⁻¹ with a resolution of 8 cm⁻¹. Every sample was measured three times and the average of the three measurements was further used for modeling. Thus, we had an average of 135 absorption spectra of soil (see Fig. 2).

Fig. 2 The near infrared spectra of 135 soil samples.

4. Results and discussion

4.1 The NIR dataset

The whole scanning range of 10 000–4000 cm⁻¹ with a resolution of 8 cm⁻¹ collected the NIR spectral responses at 1512 discrete wavenumbers per spectrum for each soil sample. The spectral absorbance includes the contributions of the chemical components and the noises that arise from the light scattering and base-line drift, due to the sample particle factors (e.g. particle size and shape, thickness and tightness, etc.). Data pretreatment is indispensable for extracting the spectral signals. Multiplicative scatter correction was used to pretreat the raw spectra of the calibration samples in each volunteer group.

The NIR dataset was constructed including the pretreated NIR data and the reference values of SOC. The whole sample pool was divided into calibration, prediction and validation sets by the framework of sample partitioning for model optimization and evaluation.

4.2 The performance of sample partitioning on LS-SVR models

All the NIR data of 135 soil samples were prepared as the original sample pool. According to the calibration–prediction–validation procedure, 35 samples were randomly selected into the independent validation sample set (totally excluded in the modeling process). The statistical data of the validation samples and the remaining samples are shown in Table 1.

Table 1 Statistics for the randomly selected validation samples and the calibration–prediction samples

	Number of samples	SOC content (%)
		Maximum value	Minimum value	Averaging value	Standard deviation
Validation	35	5.06	1.35	2.565	0.945
Calibration–prediction	100	6.42	1.10	2.728	1.093

---

The remaining 100 samples were further divided into calibration and prediction sets for modeling. The samples for calibration should not be less than those for prediction, and the calibration samples should not be significantly more than the prediction samples to prevent over-fitting. Based on these concepts and on the framework of sample partitioning, we changed the calibration–prediction partitioning ratio from 1 : 1 to 4 : 1. Practically, with a total of 100 modeling samples, we changed the number for calibration from 50 to 80 with a step of 5; thus, the number for prediction changed from 50 to 20 with a step of −5. Therefore, we generated 7 different volunteer groups (i.e. K = 7) and denoted them as G₁, G₂, G₃, G₄, G₅, G₆ and G₇. The detailed numbers for the calibration and prediction samples in each volunteer group are listed in Table 2. For model establishment, we are planning to have 100 modeling samples divided randomly into calibration set and prediction set according to the preset numbers designated in each volunteer group (see Table 2). Seven volunteer groups gave seven different partitioning cases. We try to discuss which case will provide an optimal calibration model with the highest robustness.

Table 2 Numbers of calibration and prediction samples in each volunteer group

Volunteer group	Number of calibration	Number of prediction
G1	50	50
G2	55	45
G3	60	40
G4	65	35
G5	70	30
G6	75	25
G7	80	20

---

As can be seen in Table 2, the volunteer groups are only related to the numbers of calibration and prediction samples, but a fixed number does not determine which samples are for calibration and which samples are for prediction because we used a random division strategy. This will raise the problem that different calibration samples influence the modeling results. To discuss this issue, we set the modeling sample randomly partitioned for 30 times (i.e. L = 30), obeying the preset partitioning numbers. This operation would generate 30 different pairs of calibration and prediction sets (i.e. C₁ + P₁, C₂ + P₂… C₃₀ + P₃₀) for each specific volunteer group (G_k, k = 1, 2… 7). Calibration models were established for each pair of C_l + P_l (l = 1, 2… 30) using the LS-SVR method with an interactive grid search of the tunable parameters of γ and σ² (hereafter, we discussed σ and successively obtain σ² easily).

γ changes from 10 to 200 with a step of 10, whereas σ changes consecutively from 1 to 20. The LS-SVR models corresponding to each combination of (γ, σ) were established and the parameters of γ and σ were interactively optimized on a grid. Based on the 30 different pairs of C_l + P_l (l = 1, 2… 30), the RMSEP_m and R_P,m were calculated as the stable modeling results corresponding to the interactive effect of γ and σ. The RMSEP_rsd and R_P,rsd were also calculated for evaluating the frustration of models. Successively, the optimal parameter combination can be found by searching for the minimum RMSEP_m or the alternative maximum R_P,m. This optimal result was taken as the stable and robust modeling effect for the specific volunteer group G_k. Furthermore, the optimal volunteer group can be selected by comparing the best values of RMSEP_m(G_k) and R_P,m(G_k) for the 7 volunteer groups (G_k, k = 1, 2… 7). The LS-SVR models with the optimal parameter were further selected. Table 3 lists the LS-SVR modeling results with the optimal parameters for the 7 designated volunteer groups. We can see from Table 3 that G₄ exhibits the minimum RMSEP_m and a corresponding maximum R_P,m. The relatively low values of RMSEP_rsd and R_P,rsd demonstrated that the optimal stable LS-SVR model had little predicted frustrations. It could be concluded that the optimal volunteer group for the NIR analysis of SOC is volunteer group G₄. The partition of 65 calibration samples and 35 prediction samples brought the best prospective results.

Table 3 The optimal LS-SVR modeling results for the 7 volunteer groups

Volunteer group	γ	σ	RMSEPm	RMSEPrsd	RP,m	RP,rsd
G1	120	8	0.283	0.197	0.900	0.159
G2	110	6	0.261	0.187	0.916	0.154
G3	100	7	0.258	0.190	0.923	0.148
G4	110	7	0.247	0.185	0.937	0.147
G5	130	8	0.254	0.205	0.932	0.155
G6	120	10	0.269	0.214	0.909	0.161
G7	100	9	0.285	0.217	0.885	0.175

---

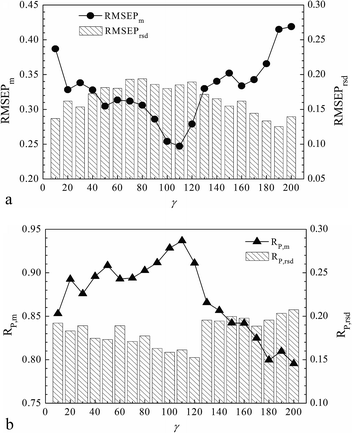
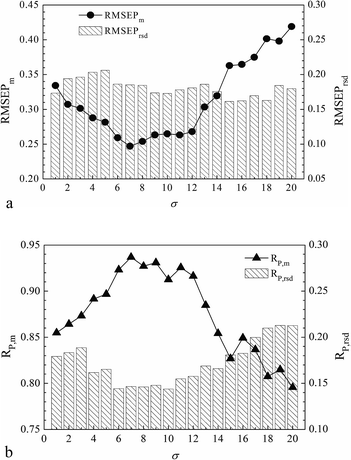
For LS-SVR modeling, it is worth noting that the two parameters of γ and σ represent the regularization extension and the kernel width when using the RBF kernel. In particular, we discussed the interactive grid searching of the parameters based on the optimal volunteer group (G₄) with the projective insight of the influence from each separate tuning of γ and σ. The model predictive results corresponding to each value of γ are shown in Fig. 3 (Fig. 3(a) distributes RMSEP_m and RMSEP_rsd, and Fig. 3(b) distributes R_P,m and R_P,rsd). Similarly, the model predictive results corresponding to each value of σ are shown in Fig. 4 (Fig. 4(a) distributes RMSEP_m and RMSEP_rsd, and Fig. 4(b) distributes R_P,m and R_P,rsd).

Fig. 3 Model predictive results corresponding to each value of γ in LS-SVR modeling (sub-figure (a) distributes RMSEP_m and RMSEP_rsd, and sub-figure (b) distributes R_P,m and R_P,rsd).

Fig. 4 Model predictive results corresponding to each value of σ in LS-SVR modeling (sub-figure (a) distributes RMSEP_m and RMSEP_rsd, and sub-figure (b) distributes R_P,m and R_P,rsd).

Fig. 3 shows that the RMSEP_rsd and R_P,rsd values varied according to γ, but most of them were smaller than 0.2, which demonstrated that the modeling frustration was small enough and the models could be considered stable. The minimum RMSEP_m was obtained when γ equaled 110 with a correspondingly highest R_P,m. Fig. 4 shows that most RMSEP_rsd and R_P,rsd derived from every value of σ were also smaller than 0.2, which in another aspect revealed the modeling stability and robustness. The minimum RMSEP_m was obtained when σ was 7, with the correspondingly highest R_P,m. In summary, the optimal LS-SVR parameters (γ, σ) were (110, 7), and the optimal RMSEP_m and R_P,m were 0.247% and 0.937, respectively. This optimal modeling result was obtained by the nonlinear LS-SVR algorithm based on the calibration–prediction sample partitioning with different ratios. We concluded that the optimal model with (γ, σ) equaling to (110, 7) was stable and robust for the calibrations in the NIR analysis of SOC.

4.3 Validation of the optimal LS-SVR model

The randomly selected 35 independent validation samples were used to evaluate the LS-SVR models on the 7 volunteer groups, using the corresponding optimal parameters. The LS-SVR models were established using the spectral data and actual SOC contents (measured by potassium dichromate oxidation). We found out the optimal parameters and determined the model regressive coefficients in the calibration–prediction process. Furthermore, the NIR predicted values for the 35 validation samples can be estimated by fitting the NIR data into the model and using the coefficients. The NIR predicted values of SOC in each volunteer group were obtained and the RMSEV and R_V for the 35 validation samples are shown in Table 4. The validation process is objective and representative because the validation samples were totally excluded in the modeling optimization process. We observe in Table 4 that the optimal modeling volunteer group G₄ outputs the optimal validation results. The predicted values were close to the actual contents with a minimum RMSEV of 0.302 (%) and a corresponding high R_V of 0.907. The correlation between the predicted values and actual contents is shown in Fig. 5. The results showed that the predicted values and the actual contents were highly correlated for SOC. The validation effect was much satisfactory for the random validation samples because we achieved the modeling stability and robustness in the process of model optimization with a prospective choice of the volunteer group for calibration–prediction partition.

Table 4 LS-SVR modeling results for validation samples based on the optimal parameters in each volunteer group

Volunteer group	RMSEVm	RMSEVrsd	RV,m	RV,rsd
G1	0.361	0.256	0.857	0.180
G2	0.332	0.244	0.872	0.183
G3	0.335	0.244	0.888	0.187
G4	0.302	0.239	0.907	0.180
G5	0.330	0.252	0.899	0.181
G6	0.342	0.277	0.870	0.184
G7	0.351	0.282	0.855	0.190

---

Fig. 5 Correlation between the NIR predicted values and actual contents of SOC.

5. Conclusions

NIR analysis requires a modeling-validation division for real samples. Differences in the partitioning and changes in the numbers of real samples in calibration set and in the prediction set lead to fluctuations and influence the stability and robustness of the modeling parameters, yielding unstable results. A representative calibration set must be extracted from the sample pool with the considerations referring to not only the samples but also the partitioning ratio. In our study, the strategy of modeling optimization was proposed based on a calibration–prediction sample partitioning. A framework for sample partitioning was built up with the consideration of the tunable ratio of numbers of calibration and prediction samples, aiming to confirm the modeling stability and robustness. This issue was addressed in the multivariate calibration involving NIR spectrometric analysis of SOC.

We created 7 volunteer groups (G_k, k = 1, 2… 7) for different ratios of calibration–prediction partitioning. For each G_k, the calibration–prediction sample partition was carried out randomly for 30 times. The LS-SVR models were established and the optimal parameters were selected for each single partition. By considering the stability and robustness, we calculated the RMSEP_m(G_k) and R_P,m(G_k), as well as the RMSEP_rsd(G_k) and R_P,rsd(G_k) based on the 30 different calibration–prediction partitions in the specific G_k. Moreover, we optimized the LS-SVR modeling parameters of γ and σ in an interactive grid search, and successively by comparing all 7 values of the RMSEP_m, we found that the optimal volunteer group was G₄. The optimal LS-SVR parameters (γ, σ) were (110, 7), and the optimal RMSEP_m and R_P,m were 0.247% and 0.937, respectively. The values of RMSEP_rsd and R_P,rsd were small enough to confirm that the models were stable and robust.

Furthermore, the optimized calibration model was evaluated by the independent validation samples for each of the 7 volunteer groups. The out-of-modeling validation effects were satisfactory for the random validation samples, and the validation optimal volunteer group was also selected as G₄. We conclude that we have achieved the modeling stability and robustness in the process of model optimization based on a discussion of the tunable ratio of numbers of calibration and prediction samples.

Acknowledgements

This study was supported by the National Natural Scientific Foundation of China (61505037), the National Spark Program of China (2014GA780009), the Pearl River S&T Nova Program of Guangzhou (201506010035) and the Natural Scientific Foundation of Guangxi (2015GXNSFBA139259).

Notes and references

1. M. C. Sarraguça, A. Paulo, M. M. Alves, A. M. Dias, J. A. Lopes and E. C. Ferreira, Anal. Bioanal. Chem., 2009, 395, 1159–1166.
2. C. Collell, P. Gou, J. Arnau and J. Comaposada, Food Chem., 2011, 129, 601–607.
3. V. R. Sinija and H. N. Mishra, LWT--Food Sci. Technol., 2009, 42, 998–1002.
4. A. Saleem, C. Canal, D. A. Hutchins, L. A. J. Davis and R. J. Green, Anal. Methods, 2011, 3, 2298–2306.
5. M. Soto-Barajas, I. Gonzalez-Martin, J. M. Hernandez-Hierro, B. Prado, C. Hidalgo and J. Etchevers, Anal. Methods, 2012, 4, 2764–2771.
6. H. Chen, W. Ai, Q. Feng, Z. Jia and Q. Q. Song, Spectrochim. Acta, Part A, 2014, 118, 752–759.
7. R. Rinnan and A. Rinnan, Soil Biol. Biochem., 2007, 39, 1664–1673.
8. M. Nocita, A. Stevens, C. Noon and B. van Wesemael, Geoderma, 2013, 199, 37–42.
9. B. Stenberg, R. A. Viscarra Rossel, A. M. Mouazen and J. Wetterlind, Adv. Agron., 2010, 107, 163–215.
10. A. M. Mouazen, M. R. Maleki, J. de Baerdemaeker and H. Ramon, Soil Tillage Res., 2007, 93, 13–27.
11. R. A. Viscarra Rossel, S. R. Cattle, A. Ortega and Y. Fouad, Geoderma, 2009, 150, 253–266.
12. B. Minasny, A. B. McBratney, V. Bellon-Maurel, J. M. Roger, A. Gobrecht, L. Ferrand and S. Joalland, Geoderma, 2011, 167–168, 118–124.
13. L. K. Sorensen and S. Dalsgaard, Soil Sci. Soc. Am. J., 2005, 69, 159–167.
14. H. T. Xie, X. M. Yang, C. F. Drury, J. Y. Yang and X. D. Zhang, Can. J. Soil Sci., 2011, 91, 53–63.
15. R. S. Bricklemyer and D. J. Brown, Comput. Electron. Agr., 2010, 70, 209–216.
16. T. H. Waiser, C. L. S. Morgan, D. J. Brown and C. T. Hallmark, Soil Sci. Soc. Am. J., 2007, 71, 389–396.
17. C. D. Christy, Comput. Electron. Agr., 2008, 61, 10–19.
18. A. Stevens, B. van Wesemael, H. Bartholomeus, D. Rosillon, B. Tychon and E. Ben-Dor, Geoderma, 2008, 144, 395–404.
19. P. V. Ajayakumar, D. Chanda, A. Pal, M. P. Singh and A. Samad, J. Pharm. Biomed. Anal., 2012, 58, 157–162.
20. H. Chen, Q. Feng, Z. Jia and Q. Q. Song, Asian J. Chem., 2014, 26, 4839–4844.
21. R. K. H. Galvao, M. C. U. Araujo, G. E. Jose, M. J. C. Pontes, E. C. Silva and T. C. B. Saldanha, Talanta, 2005, 67, 736–740.
22. M. Silva, M. H. Ferreira, J. W. B. Braga and M. M. Sena, Talanta, 2012, 89, 342–351.
23. M. Zeaiter, J. M. Roger and V. Bellon-Maurel, TrAC, Trends Anal. Chem., 2005, 24, 437–445.
24. X. Shao, X. Bian, J. Liu, M. Zhang and W. Cai, Anal. Methods, 2010, 2, 1662–1666.
25. Z. P. Chen, L. J. Zhong, A. Nordon, D. Littlejohn, M. Holden, M. Fazenda, L. Harvey, B. McNeil, J. Faulkner and J. Morris, Anal. Chem., 2011, 83, 2655–2659.
26. S. R. Delwiche and J. B. Reeves III, The effect of spectral pre-treatments on the partial least squares modelling of agricultural products, J. Near Infrared Spectrosc., 2004, 12, 177–182.
27. B. Igne and C. R. Hurburgh Jr, J. Chemom., 2010, 24, 75–86.
28. N. C. Dingari, I. Barman, G. P. Singh, J. W. Kang, R. R. Dasari and M. S. Feld, Anal. Bioanal. Chem., 2011, 400, 2871–2880.
29. H. Chen, G. Tang, Q. Song and W. Ai, Anal. Lett., 2013, 46, 2060–2074.
30. A. Borin, M. F. Ferrao, C. Mello, D. A. Maretto and R. J. Poppi, Anal. Chim. Acta, 2006, 579, 25–32.
31. R. G. Brereton and G. R. Lloyd, Analyst, 2010, 135, 230–267.
32. I. Barman, N. C. Dingari, G. P. Singh, J. S. Soares, R. R. Dasari and J. M. Smulko, Anal. Chem., 2012, 84, 8149–8156.
33. H. Chen, T. Pan, J. Chen and Q. Lu, Chemom. Intell. Lab. Syst., 2011, 107, 139–146.
34. T. Pan, Z. Chen, J. Chen and Z. Liu, Anal. Methods, 2012, 4, 1046–1052.
35. Z. Liu, B. Liu and T. Pan, Spectrochim. Acta, Part A, 2013, 102, 269–274.
36. H. Z. Chen, Q. Q. Song, G. Q. Tang and L. L. Xu, J. Cereal Sci., 2014, 60, 595–601.
37. H. Z. Chen, W. Ai, Q. X. Feng and G. Q. Tang, Anal. Methods, 2015, 7, 2869–2876.
38. N. Cristianini and J. Shawe-Taylor, An introduction to support vector machines and other kernel-based learning methods, Cambridge University Press, New York, USA, 2000.
39. R. K. Lu, Methods for chemical analysis of soil agriculture, China agricultural science and technology press, Beijing, China, 2000.

---