Solubility of DL-serine and DL-phenylalanine in aqueous mixtures of dimethyl sulfoxide and solvation thermodynamics
Aslam Hossaina,
Sanjay Royb,
Srabani Ghosha,
Samiran Mondala and
Bijoy Krishna Dolui*a
aDepartment of Chemistry, Visva-Bharati, Santiniketan, 731235, West Bengal, India. E-mail: bijoy_dolui@yahoo.co.in
bDepartment of Chemistry, Shibpur Dinobundhoo Institution (college), Howrah-711102, West Bengal, India
First published on 11th August 2015
Abstract
The standard free energies (ΔG0t(i)) and entropies (ΔS0t(i)) of transfer of DL-serine and DL-phenylalanine from water (1) to aqueous mixtures of dimethylsulfoxide (DMSO) (2) at 298.15 K are reported in the present study. The transfer energies have been determined from solubility measurements of the amino acids. The solubility is measured at different temperatures i.e. from 288.15 to 308.15 K by an ‘analytical gravimetric method’. The chemical parts of the free energies (ΔG0t,ch(i)) and entropies (TΔS0t,ch(i)) of transfer of the amino acids have been computed by subtracting the cavity effects and dipole–dipole interaction effects from the total transfer energies. The characteristics of the solvation thermodynamics of the amino acids in an aqua-organic solvent system are studied and discussed in the present manuscript.
1. Introduction
It is well known that proteins play key roles in nearly all biological processes. The proteins are built using amino acids as the structural units. The side chains of these building blocks differ in size, shape, charge, hydrogen bonding capacity, acidity, basicity, hydrophilicity, hydrophobicity, chemical reactivity, etc. The zwitterionic behavior of amino acids is also an important guiding factor in building different proteins.The native state of a protein is determined by the character and sequence of its constituent amino acids and also by the solvent environment in which it is present. Protein folding is an important process that affects nearly every aspect of their biological activities. The conformation of a protein in solution is generally a function of electrostatic, hydrogen bonding, van der Waals forces, acid–base interactions, hydrophobic and hydrophilic interactions among the amino acid residues.1 Denaturation or defolding of a protein is also an essential process for the dissolution and purification of proteins during their extraction from natural sources.
In this respect, the knowledge of the solvation thermodynamics of proteins as well as amino acids in different solutions is necessary.1–19 For a long time researchers had drawn their attention to determine the solubilities as well as solvation thermodynamic data of amino acids in different solvent systems.1–19 The purposes of such studies were to gain clear ideas about the various aspects of protein folding–unfolding and protein hydration2,3 with biological as well as pharmaceutical and industrial importance.6–9 Various research groups in the world wide2–22 are working on the solvation thermodynamics of some amino acids in aquo-organic, aqueous electrolyte and in non-aqueous solvent systems. Solvation thermodynamic data like free energy of transfer of the amino acids can help to predict the stability of different conformations of the biomolecules like amino acids,3–9 peptides10,17 as well as proteins.1,15,31 Some authors23–26 also believed that entropy of transfer of amino acids can be used as a structural probe to recognize the structural changes taking place in various solvent systems in presence of amino acids.
All these researcher also tried to explore the ideas about the relative stabilization of these amino acids and other biomolecules in aqua-organic,2,3,5,10–16 aqueous electrolyte6,7,17,18 and in non-aqueous mixtures27–29 with respect to water and the complex solute–solvent and solvent–solvent interactions therein.
Presently, DMSO with immense biological importance20 is chosen here as co-solvent with H2O to get further broader insight about the aqua-organic chemistry for amino acid solvation.
DMSO possesses two hydrophobic methyl groups with +I effect and these hydrogen atoms of two CH3– groups are of acidic character.37 Also it has increased basicity as well as protophilic dipolar aprotic character compared to H2O. On the other hand between the amino acid DL-serine and DL-phenylalanine here under study the first and the second one is composed of hydrophilic –OH group and hydrophobic –C6H5 group respectively. Therefore study of solvation mechanism of these amino acids may be rewarding in H2O–DMSO mixtures. Considering these point of views and followed by previous works,19 we are presenting the standard transfer free energy (ΔG0t(i)) and entropies (ΔS0t(i)) of amino acids like DL-serine and DL-phenylalanine from pure water to aqua-organic mixture of DMSO at 298.15 K.
In such situation in the present study we have tried to get some important ideas about structural eccentricities of water23 and the role of highly complex aquo-organic chemistry in the context of stabilization of the same.
The solvation characters of this aqua-organic solvent mixture undergo gradual but material change compared to pure solvent system10–16 with respect to amino acid solvation. The results found in the present study i.e. in this aqua-organic binary solvent system are likely to be very much useful to understand the solvation mechanism of amino acid and amino acid induced solvent–solvent interaction in aqua-organic binary solvent mixture and fill up the needs of the thermodynamic data in chemical, pharmaceutical, cosmetics, food and in industrial sciences.
2. Experimental section
2.1. Materials and their purifications
Amino acids, DL-serine (>99.0% E Merck) and DL-phenylalanine (>99.0%, E-Merck), were used after drying in a vacuum desiccator without further purification.11Dimethylsulfoxide (DMSO)29,30 (>99.8%, Sigma Aldrich) was first dried over fused CaCl2 for 3–4 days, decanted and then was distilled under reduced pressure. The distilled sample was preserved in a well stoppered Jena bottle in desiccators and redistilled before use. The triple distilled water is used in the whole experimental solutions and for other needs.
2.2. Method
Aqueous solvent mixtures of DMSO (2) that have been used were 0, 5.4, 13.3, 25.6, 47.9 and 100 mol% of DMSO. The mixed solvents were prepared by mixing triple distilled H2O (1) and DMSO (2) by weight using a Mettler balance having a precision of ±0.1 mg.The pure solvents and solvent mixtures were preserved in well stoppered glass bottles and all were protected by storing in desiccators when not in use.
The ‘analytical gravimetric’ method26,31 consists of the preparation of a saturated solution at the desired temperatures. The jacketed glass cell was charged with known masses (±0.1 mg) of the binary mixed solution and with each amino acid in a small excess to the expected saturation limit. To reach equilibrium conditions the solution was continuously stirred for 24 h and, after that, the solutions were allowed to settle for at least 12 h before sampling with preheated pipette. The samples (5 cm3) were withdrawn from the supernatant phase, inserted into glass vessels and immediately weighted.
The next step was to evaporate all solution from the sample, and to dry completely in a drying stove for 2 days. Finally, the samples were cooled in a dehydrator with silica gel for 1 day and weighted; the process was regularly repeated until a constant mass value was achieved.
The mass of dissolved amino acids were calculated from the knowledge of the initial electrolyte concentration in the solution and the weight of the glass vessels empty, with the saturated solution and with the dried sample.
Four sets of measurements for the entire aqueous electrolyte mixtures were made for all temperatures by equilibrating the solutions from both above and below (±0.1 K) the required temperatures i.e. 288.15, 293.15, 298.15, 303.15 and 308.15 K and the solubilities were found to agree with maximum 2.4% uncertainties.
3. Theoretical
3.1. Calculations of thermodynamic parameters
The Gibbs energy of solutions (ΔG0sol(i)) on molal scale were computed at different temperatures for each solvent mixture using eqn (1) like previous studies.11,28,29
ΔG0sol(i) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sγ ≈ −RT Sγ ≈ −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S S
| (1) |
Amino acids are likely to be zwitterions in solutions. So they are expected to have large dipole–dipole interaction among themselves. Therefore, the activity coefficient factor −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ may contribute to ΔG0sol(i). In some previous studies Held and coworkers9 measured the activity coefficients of some amino acids like glycine, proline, hydroxyproline, L-leucine, L-methionine, etc., in aqueous systems. They found that the values of activity coefficient (γ) were nearly unity for such amino acids in lower concentrations. It is to be noted here that the mole fractions of amino acids present in different compositions of the present aqueous DMSO solvent system, as calculated from solubility values (shown in Table 3) are negligibly small. Therefore the activity coefficients of the present solute–solvent systems are taken as unity in calculating of ΔG0sol(i) as is usually done for non-electrolytes.23,24,28,29
γ may contribute to ΔG0sol(i). In some previous studies Held and coworkers9 measured the activity coefficients of some amino acids like glycine, proline, hydroxyproline, L-leucine, L-methionine, etc., in aqueous systems. They found that the values of activity coefficient (γ) were nearly unity for such amino acids in lower concentrations. It is to be noted here that the mole fractions of amino acids present in different compositions of the present aqueous DMSO solvent system, as calculated from solubility values (shown in Table 3) are negligibly small. Therefore the activity coefficients of the present solute–solvent systems are taken as unity in calculating of ΔG0sol(i) as is usually done for non-electrolytes.23,24,28,29
This assumption will not be difficult to understand because the factor containing the ratio of activity coefficient, −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γs/γR (‘s’ for H2O–DMSO and ‘R’ for reference solvent, H2O), in determining transfer free energies, ΔG0t(i) [ΔG0t(i) = sΔG0sol(i) − RΔG0sol(i)], which is our main concern, is likely to be negligibly small.
γs/γR (‘s’ for H2O–DMSO and ‘R’ for reference solvent, H2O), in determining transfer free energies, ΔG0t(i) [ΔG0t(i) = sΔG0sol(i) − RΔG0sol(i)], which is our main concern, is likely to be negligibly small.
To get the precise value of ΔG0sol(i) and to quantify the effect of temperature on ΔG0sol(i) the method of least squares is used in the form of eq (2).29
ΔG0sol(i) = a + bT + cT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T T
| (2) |
| ΔG0t(i) = sΔG0sol(i) − RΔG0sol(i) | (3) |
ΔG0t(i) = (as − aR) + (bs − bR)T + (cs − cR)T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T − RT T − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ms/MR) ln(Ms/MR)
| (4) |
ΔS0t(i) = (bR − bs) + (cR − cS)(1 + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) + R T) + R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ms/MR) ln(Ms/MR)
| (5) |
Now ΔX0t(i) (where X = G or S) may be ascribed as the sum of the following terms (assuming dipole induced dipole term to be negligibly small).23,26
| i.e. ΔX0t(i) = ΔX0t,cav(i) + ΔX0t,d–d(i) + ΔX0t,ch(i) | (6) |
| σs = mole fraction of water × hard-sphere diameter of water + mole fraction of DMSO × hard-sphere diameter of DMSO. |
| Chemical name | Chemical structure | Source | Initial puritya (fraction) | Purification method | Final purity (fraction) |
|---|---|---|---|---|---|
| a Declared by the supplier.b Gas−liquid chromatography. | |||||
| DL-Phenylalanine | 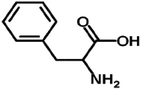 |
E. Merck | 99.8% (mass) | Drying in vacuum desiccator | 99.9% (mass) |
| DL-Serine | 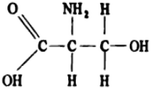 |
E. Merck | 99.8% (mass) | Drying in vacuum desiccator | 99.9% (mass) |
| Dimerthylsulfoxide |  |
Sigma Aldrich | 99.8% (mass) | Distilled under reduced pressure | 99.98% (mass) (analysis method: GCb) |
| Sodium hydroxide | NaOH | GR, E. Merck | 99% (mass) | — | 99% |
| Water | H2O | Distillation | — | ||
| Formaldehyde | HCHO | GR, E. Merck | 99% (mass) | Distillation | 99% (mass) |
| Mol% DMSO | Mole fraction (zs) | Mole fraction (zR) | Molar mass (MS) | 103 ds (kg m−3) | Molar vol. (Vs) | σs (nm) | σs−x (nm) | Dipole moment (μs) | α (×10−3) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Phe | Ser | |||||||||
| a #, *For the ref. 31. | ||||||||||
| 0.00 | 0.000 | 1.000 | 18.015 | 0.997# | 18.06921 | 0.274 | 0.467 | 0.433 | 1.831 | 0.257* |
| 5.40 | 0.054 | 0.946 | 21.260 | 1.002 | 21.21756 | 0.286 | 0.473 | 0.440 | 1.941 | 0.296 |
| 13.30 | 0.133 | 0.867 | 26.010 | 1.009 | 25.77800 | 0.303 | 0.482 | 0.448 | 2.105 | 0.353 |
| 25.60 | 0.256 | 0.744 | 33.400 | 1.021 | 32.71303 | 0.329 | 0.495 | 0.461 | 2.359 | 0.442 |
| 47.90 | 0.479 | 0.521 | 46.810 | 1.042 | 44.92322 | 0.378 | 0.519 | 0.486 | 2.821 | 0.602 |
| 100 | 1.000 | 0.000 | 78.130 | 1.091# | 71.61320 | 0.491 | 0.576 | 0.542 | 3.900 | 0.982 |
Keesom-orientation expression30,32 is used to calculate ΔG0d–d(i) and sΔS0d–d(i) as:
| ΔG0t,d–d(i) = (sΔG0d–d(i) − RΔG0d−d(i)) | (7) |
| ΔS0t,d–d(i) = (sΔS0d–d(i) − RΔS0d–d(i)) | (8) |
| sΔG0d−d(i) = −(8Π/9)N2μ2sμ2xσ−3s−x(kT)−1V−1s = A/TVs | (9) |
The dipole moment of the mixed binary solvent system in a particular composition is calculated as:38 μs = μ of reference solvent (H2O) × mole fraction of reference solvent (H2O) + μ of co-solvent (DMSO) × mole fraction of co-solvent (DMSO).
σs−x represents the distance at which the attractive and repulsive interactions between the solvent and solute molecules are equal and is generally equal to 1/2(σs + σx) where σs and σx are the hard sphere diameters of co-solvent and solute amino acid molecules respectively (Tables 2 and 6).
Here ΔS0d−d(i) can be written as follows:
| sΔS0d–d(i) = −{δsΔG0d–d(i)/δT}p | (10) |
| TsΔS0d–d(i) = sΔG0d–d(i)[1 + Tα]23,29 | (11) |
α = (δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vs/δT)p = −(δ Vs/δT)p = −(δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ds/δT) ds/δT)
| (12) |
As in the earlier studies,32,33 in order to get the ΔX0t,d–d(i) term on the mole fraction scale, ΔX0t,d–d(i) was again multiplied by Xsl, which is the actual mole fraction of the organic co-solvent in the vicinity of the solute for the contribution of dipole–dipole interaction,33 which was estimated using the eqn (13) as follow;32
| Xs1 = Xs(μs/σs3)/(μR/σR3) | (13) |
On the other hand ΔX0t,ch(i) values of amino acids were calculated after the subtraction of ΔX0t,cav(i) and ΔX0t,d–d(i) from the total i.e. ΔX0t(i). The values of ΔX0t,cav(i), ΔX0t,d–d(i) and ΔX0t,ch(i) are presented in Table 6.
4. Result and discussion
4.1. Analysis of solubility data
The solubility of DL-serine and DL-phenylalanine increases with temperature in a particular composition of water–DMSO mixed solvent system. But the solubility of DL-serine is higher than DL-phenylalanine in 0, 20 and 40 wt % of water–DMSO composition and the reverse is true in 60, 80 and 100 wt% of the same at any temperature. This is due to the involvement of structural effect of solutes and solvents i.e. DL-serine, DL-phenylalanine, water and DMSO. Pure water has strong intermolecular hydrogen bonding capability. On the other hand the![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) S
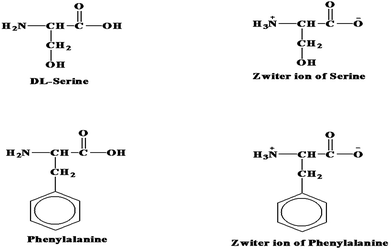
S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety of DMSO allows weak acid-base, anionophilic and cationophilic interaction for –COO− and NH3+ moieties of both the amino acids. In DL-serine there is a hydrophilic –OH group (Scheme 1). In contrast there is a bulky hydrophobic moiety like –C6H5 instead of –OH moiety in DL-phenylalanine (Scheme 1). The –OH group can take part in hydrophilic interaction with the solvent molecules through H-bonding and acid–base interactions which lead to more solubility for the amino acid DL-serine, but in case of DL-phenylalanine, the presence of such bulky hydrophobic moiety reduces the hydrophilic interaction with the solvent molecule, so that the solubility become higher for the former than the latter in water-rich composition of water–DMSO solvent system. The reverse is true due to the increased concentration of larger dipolar aprotic DMSO co-solvent from 60 to 100 wt% of the same in such aqueous DMSO binary solvent mixtures.
O moiety of DMSO allows weak acid-base, anionophilic and cationophilic interaction for –COO− and NH3+ moieties of both the amino acids. In DL-serine there is a hydrophilic –OH group (Scheme 1). In contrast there is a bulky hydrophobic moiety like –C6H5 instead of –OH moiety in DL-phenylalanine (Scheme 1). The –OH group can take part in hydrophilic interaction with the solvent molecules through H-bonding and acid–base interactions which lead to more solubility for the amino acid DL-serine, but in case of DL-phenylalanine, the presence of such bulky hydrophobic moiety reduces the hydrophilic interaction with the solvent molecule, so that the solubility become higher for the former than the latter in water-rich composition of water–DMSO solvent system. The reverse is true due to the increased concentration of larger dipolar aprotic DMSO co-solvent from 60 to 100 wt% of the same in such aqueous DMSO binary solvent mixtures.
4.2. Solvation of the amino acids
The specifications of chemical samples used in the experimental are given in the Table 1. The experimental solubility (mol kg−1) of the amino acids (DL-serine, DL-phenylalanine) are measured on molal scale and are listed in Table 3. Standard uncertainties of solubilities at all temperatures and compositions are found to be ±0.00004 and cited in the Table 3.| T/K | Solubility (S) | |||||
|---|---|---|---|---|---|---|
| Mass fraction of DMSO (X) | ||||||
| 0.00 | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 | |
| mol% of DMSO | ||||||
| 0.00 | 5.40 | 13.30 | 25.60 | 47.90 | 100 | |
| a # u(T) = ± 0.1. u(x) ±0.01. *u(S) = ±0.00004. | ||||||
| DL-Phenylalanine | ||||||
| 288.15 | 0.0657 | 0.0496 | 0.0304 | 0.0117 | 0.0084 | 0.0050 |
| 293.15 | 0.0690 | 0.0526 | 0.0342 | 0.0140 | 0.0096 | 0.0059 |
| 298.15 | 0.0726 | 0.0558 | 0.0366 | 0.0162 | 0.0104 | 0.0065 |
| 303.15 | 0.0762 | 0.0589 | 0.0392 | 0.0178 | 0.0118 | 0.0072 |
| 308.15 | 0.0798 | 0.0629 | 0.0418 | 0.0208 | 0.0130 | 0.0082 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| DL-Serine | ||||||
| 288.15 | 0.4604 | 0.2142 | 0.0702 | 0.0180 | 0.0035 | 0.0017 |
| 293.15 | 0.4960 | 0.2252 | 0.0739 | 0.0206 | 0.0045 | 0.0022 |
| 298.15 | 0.5292 | 0.2365 | 0.0778 | 0.0227 | 0.0053 | 0.0025 |
| 303.15 | 0.5580 | 0.2456 | 0.0822 | 0.0254 | 0.0078 | 0.0031 |
| 308.15 | 0.5858 | 0.2504 | 0.0894 | 0.0285 | 0.0102 | 0.0039 |
The values of ΔG0t(i) are cited in Table 5 which are represented by the Fig. 1. The positive increment of ΔG0t(i) values for the both amino acids at 298.15 K with increased concentration (mol%) of DMSO in H2O–DMSO mixed solvent system indicates destabilization of the same. But the positive increment is higher for DL-serine than the DL-phenylalanine. This indicates that the former amino acid gains lesser stability in H2O–DMSO mixed solvent system than the latter due to different types of solute–solvent interactions like cavity forming, dipole–dipole and chemical interactions. The more or less gradual increase of components of ΔG0t(i) due to dipole–dipole interaction, ΔG0t,d–d(i) and cavity effect, ΔG0t,cav(i) are also responsible for this trend. Since the total transfer free energies, ΔG0t(i) of amino acid is mainly the sum of ΔG0t,cav(i), ΔG0t,d–d(i) and ΔG0t,ch(i) (Table 6) and so it depends on many types of interactions. However, the actual stability order of the amino acids is somewhat complex to explain by considering total transfer free energies with the variation of solvent composition. So that the ΔG0t,ch(i)-composition profiles can be used to explain the results in terms of chemical interactional effects. The ΔG0t,ch(i) values of the amino acids with DMSO composition are presented in Table 6.
 | ||
| Fig. 1 Variation of ΔG0t(i) in kJ mol−1 of DL-phenyl alanine and DL-serine in aqueous mixtures of DMSO at 298.15 K. | ||
The ΔG0t,ch(i) values are obtained after elimination of ΔG0t,cav(i) and ΔG0t,d–d(i) from ΔG0t(i) of each amino acid. The amino acids become stabilized (Table 6) by the cavity forming interaction in the mixed aqueous DMSO solvent mixtures due to the involvement of larger (σDMSO = 4.91 Å (ref. 32)) DMSO co-solvent molecules. But the dipole–dipole interaction between solute (amino acids) and mixed aqueous solvent (H2O–DMSO) systems become unfavorable for the stabilization of both the amino acids. The stability due to dipole–dipole interaction, ΔG0t,d–d(i) of DL-phenylalanine is higher than DL-serine for the difference in size and dipole moment of the involved solutes and solvents under study.
The term ΔG0t,ch(i) represents the chemical interactions which is actually arises due to H-bonding, acid-base, dispersion, hydrophilic, hydrophobic and hard–soft interactions. The chemical interactions impart a gradual destabilization for both the amino acid i.e. DL-phenylalanine and DL-serine. In the main the extent of destabilization is comparatively greater for DL-serine than DL-phenylalanine.
DL-serine having hydrophilic side chain (–CH2OH) along with –COO− and NH3+ moieties are strongly interacted (greater association) by hydrogen bonding, acid–base, hydrophilic and hydrophobic hydration capability of reference solvent, protic H2O molecule in the water-rich region of such protic and dipolar aprotic solvent mixtures.
But the gradual destabilization of the same occurs with the increase of concentration of co-solvent, DMSO having weaker capacity of hydrogen bonding, acid–base, hydrophobic and hydrophilic interactions. Here co-solvent, DMSO with its larger size32 and hence polarizability (greater softness) will impart dispersion interaction for DL-serine (5.93 Å). But the weakening of the polarity oriented former types of interactions plays dominant role over the latter type of interaction with the increased concentration of DMSO in such binary solvent mixtures and hence the nature of stability is reflected in Fig. 2.
 | ||
| Fig. 2 Variation of ΔG0t,ch(i) in kJ mol−1 of DL-phenyl alanine and DL-serine in aqueous mixtures of DMSO at 298.15 K. | ||
On the other hand DL-phenylalanine having only bulky hydrophobic side chain (–CH2C6H5) can take part in lesser extent of hydrogen bonding, acid–base, hydrophobic and hydrophilic interactions. Therefore it will be destabilized in water-rich region of this water–DMSO solvent mixture. DL-phenylalanine will take part in dispersion as well as soft–soft interaction with larger co-solvent DMSO molecules in greater extent than DL-serine due to the larger size of the former. Therefore, DL-phenylalanine will comparatively be more stabilized than DL-serine with the increased concentration of DMSO in water–DMSO mixtures.
As the concentration of DMSO is increased, the association between H2O and DMSO (Scheme 2(A)) may occur20,35 resulting comparatively larger associated solvent molecules. The self association (dimerisation) of DMSO (Scheme 2(B))29,34 occurs in the higher concentration of DMSO in the mixed solvent system. Now the associated or self associated larger size molecule of mixed solvent takes part in dispersion interaction for both the α-amino acids.
 | ||
| Scheme 2 (A) Associated form of dimethylsulfoxide and water molecules; (B) dimerised form of dimethylsulfoxide. | ||
The size of DL-phenylalanine (6.60 Å) is larger than DL-serine (5.93 Å). Therefore the dispersion interaction will be stronger for the former than the latter.
It is to be noted that the stability of DL-serine is greater than DL-Phenylalanine in 100 wt % of DMSO. Here the dimerised (DMSO)2 (Scheme 2(B))29,34 exerts dispersion as well as acid-base, hydrogen bonding and cationophilic/anionophilic interaction for both the amino acids. These chemical interactions altogether will be stronger for DL-serine than DL-phenylalanine due to the presence of polar –OH group in the side chain of the former.
4.3. Role of amino acids for controlling solvent–solvent interaction in protic and dipolar aprotic binary solvent mixtures
The variations of TΔS0t(i) (Fig. 3) values of the amino acids with the increased concentration of DMSO in H2O –DMSO solvent system are presented in the Tables 3 and 4. | ||
| Fig. 3 Variation of TΔS0t(i) in kJ mol−1 of DL-phenyl alanine and DL-serine in aqueous mixtures of DMSO at 298.15 K. | ||
| 288.15 K | 293.15 K | 298.15 K | 303.15 K | 303.18 K | |||||
|---|---|---|---|---|---|---|---|---|---|
| S | ΔG0sol | S | ΔG0sol | S | ΔG0sol | S | ΔG0sol | S | ΔG0sol |
| a #Standard uncertainties of temperature u(T) = ±0.1 K. | |||||||||
| DL-Phenylalanine | |||||||||
| 0.0657 | 6.5226 | 0.0690 | 6.5163 | 0.0726 | 6.5014 | 0.0762 | 6.4885 | 0.0798 | 6.4772 |
| 0.0496 | 7.1961 | 0.0526 | 7.1778 | 0.0558 | 7.1538 | 0.0589 | 7.1375 | 0.0629 | 7.0869 |
| 0.0304 | 8.3688 | 0.0342 | 8.2270 | 0.0366 | 8.1992 | 0.0392 | 8.1637 | 0.0418 | 8.1338 |
| 0.0117 | 10.6564 | 0.0140 | 10.4039 | 0.0162 | 10.2195 | 0.0178 | 10.1536 | 0.0208 | 9.9219 |
| 0.0084 | 11.4502 | 0.0096 | 11.3234 | 0.0104 | 11.3182 | 0.0118 | 11.1896 | 0.0130 | 11.1261 |
| 0.0050 | 12.6931 | 0.0059 | 12.5099 | 0.0065 | 12.4832 | 0.0072 | 12.4347 | 0.0082 | 12.3067 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| DL-Serine | |||||||||
| 0.4604 | 1.8582 | 0.4940 | 1.7188 | 0.5292 | 1.5775 | 0.5580 | 1.4704 | 0.5858 | 1.3700 |
| 0.2142 | 3.6914 | 0.2252 | 3.6334 | 0.2365 | 3.5739 | 0.2456 | 3.5388 | 0.2504 | 3.5272 |
| 0.0702 | 6.3639 | 0.0739 | 6.3491 | 0.0778 | 6.3299 | 0.0822 | 6.2974 | 0.0894 | 6.1862 |
| 0.0180 | 9.6244 | 0.0206 | 9.4625 | 0.0227 | 9.3833 | 0.0254 | 9.2574 | 0.0285 | 9.1151 |
| 0.0035 | 13.5476 | 0.0045 | 13.1701 | 0.0053 | 12.9891 | 0.0078 | 12.2330 | 0.0102 | 11.7475 |
| 0.0017 | 15.2776 | 0.0022 | 14.9143 | 0.0025 | 14.8517 | 0.0031 | 14.5587 | 0.0039 | 14.2106 |
| Solvent mass fractions (x2) | a (kJ mol−1) | b (kJ mol−1 K−1) | c (kJ mol−1 K−1) | ΔG0t(i) (kJ mol−1) | TΔS0t(i) (kJ mol−1) |
|---|---|---|---|---|---|
| a u(T) = ±0.1. u(x2) ±0.01. | |||||
| DL-Phenylalanine | |||||
| 0.000 | 3.14 | 0.0889 | −0.01363 | 0 | 0 |
| 0.200 | −20.20 | 0.6441 | −0.09694 | 0.257 | 0.831 |
| 0.400 | 128.55 | −2.6431 | 0.39304 | 0.777 | 2.885 |
| 0.600 | 101.82 | −1.8612 | 0.27276 | 2.226 | 6.453 |
| 0.800 | 17.56 | −0.0522 | 0.00545 | 2.408 | 5.487 |
| 1.000 | 62.53 | −1.0279 | 0.15135 | 3.034 | 6.696 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| DL-Serine | |||||
| 0.000 | 65.87 | −1.3047 | 0.19115 | 0 | 0 |
| 0.200 | 65.63 | −1.3458 | 0.19967 | 1.569 | −4.759 |
| 0.400 | −95.93 | 2.3436 | −0.35114 | 3.821 | −4.437 |
| 0.600 | 12.86 | 0.0611 | −0.01278 | 6.252 | 0.919 |
| 0.800 | −361.94 | 8.9363 | −1.34871 | 8.904 | 5.626 |
| 1.000 | −71.95 | 2.2443 | −0.34074 | 13.136 | 6.358 |
| Solvent mass fractions (x2) | ΔG0t(i) (kJ mol−1) | ΔG0t,cav(i) (kJ mol−1) | ΔG0t,d−d(i) (kJ mol−1) | ΔG0t,ch(i) (kJ mol−1) | TΔS0t(i) (kJ mol−1) | ΔH0t,cav(i) (kJ mol−1) | TΔSot,cav(i) (kJ mol−1) | TΔS0t,d−d(i) (kJ mol−1) | TΔS0t,ch(i) (kJ mol−1) |
|---|---|---|---|---|---|---|---|---|---|
| a u(T) = ±0.1. u(x2) ±0.01. Here σH2O = 2.74 Å,32 σDMSO = 4.91 Å,32 μHOH = 1.83 D (ref. 32) and μDMSO = 3.90 D.32 The required hard sphere diameter of DL-phenylalanine and DL-serine is 6.60 and 5.93 Å respectively. Dipole-moment values of DL-phenylalanine and DL-serine are 2.480 D (ref. 35) and 11.10 D (ref. 36) respectively. | |||||||||
| DL-Phenylalanine | |||||||||
| 0.000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.200 | 0.257 | −1.580 | 0.011 | 1.826 | 0.831 | −1.090 | 0.490 | 0.010 | 0.331 |
| 0.400 | 0.777 | −3.200 | 0.050 | 3.927 | 2.885 | −1.820 | 1.380 | 0.045 | 1.460 |
| 0.600 | 2.226 | −4.870 | 0.121 | 6.975 | 6.453 | −2.090 | 2.780 | 0.108 | 3.565 |
| 0.800 | 2.408 | −6.670 | 0.236 | 8.842 | 5.487 | −1.110 | 5.560 | 0.199 | −0.272 |
| 1.000 | 3.034 | −7.840 | 0.398 | 10.476 | 6.696 | 16.900 | 24.740 | 0.294 | −18.338 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| DL-Seine | |||||||||
| 0.000 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.200 | 1.569 | −1.450 | 0.307 | 2.712 | −4.759 | −0.892 | 0.558 | 0.294 | −5.611 |
| 0.400 | 3.821 | −2.960 | 1.310 | 5.471 | −4.437 | −1.500 | 1.460 | 1.120 | −7.017 |
| 0.600 | 6.252 | −4.550 | 3.170 | 7.632 | 0.919 | −1.710 | 2.840 | 2.860 | −4.781 |
| 0.800 | 8.904 | −6.310 | 6.340 | 8.874 | 5.626 | −0.879 | 5.431 | 5.470 | −5.275 |
| 1.000 | 9.571 | −7.620 | 10.700 | 6.491 | 6.358 | 14.300 | 21.920 | 8.270 | −23.832 |
The TΔS0t(i) value is composed of cavity, dipole–dipole and chemical interaction effect as-
| TΔS0t(i) = TΔS0t,cav(i) + TΔS0t,d–d(i) + TΔS0t,ch(i) | (14) |
The first two energy terms stand for the difference in the entropy change involved in creating appropriate cavities for accommodating the amino acids and dipole–dipole interaction between the amino acid dipole with the solvent dipole, respectively. TΔS0t,cav(i) and TΔS0t,d–d(i) values are presented in Table 6.
TΔS0t,ch(i) term i.e. the chemical transfer entropy change, (Fig. 4) stands for the combined effects of various chemical interactions between solvent molecules induced by the amino acids. The values of TΔS0t,ch(i) of the amino acids are summarized in Table 6.
 | ||
| Fig. 4 Variation of TΔS0t,ch(i) in kJ mol−1 of DL-phenyl alanine and DL-serine in aqueous mixtures of DMSO at 298.15 K. | ||
At water rich region with the introduction of DMSO molecules the hydrogen bonds between the water molecules are broken down and immediately the free water molecules are interacted with the solute molecules through hydrogen bonding. This type of interaction occurs strongly and easily with the molecules having polar side chain with stronger hydrogen bonding capacity. Therefore water molecules are involved in the interaction with DL-serine to show its lesser disorderness [negativeTΔS0t,ch(i)] in the water-rich region (up to 60 wt% H2O) of this water–DMSO binary solvent system. DL-Serine induces the association between H2O and DMSO (Scheme 2(A))20 resulting comparatively larger associated solvent molecules with lesser disorderness involving negative TΔS0t,ch(i) as the concentration of DMSO is increased (80 wt% DMSO). The self association (dimerisation) of DMSO (Scheme 2(B))29,34 is induced in the highest concentration of DMSO in the mixed solvent system imparting the lowest disorderness.
But in presence of DL-phenylalanine, having larger hydrophobic phenyl moiety the disorderness of the solvent molecules becomes more favorable up to about 60 wt% DMSO concentration due to weaker solute–solvent interaction. After that up to 100 wt% the disorderness is gradually decreased. With the increment of the concentration of DMSO in this mixed solvent system dimerisation of DMSO (Scheme 2(B))29,34 occurs progressively. Larger self-associated dimerised, (DMSO)2 is induced to take part in the strongest dispersion interaction towards the amino acid, DL-phenyl alanine.
The numbers of free DMSO molecules become lower due to such dimerisation of it. Therefore the overall entropy change due to DL-phenylalanine induced chemical interactions results more negative values of transfer entropy [TΔS0t,ch(i)] that is the lowest disorderness in this aqueous DMSO solvent mixture (Fig. 4).
5. Conclusion
From the above surveillance it may be concluded that the stability of both the amino acid, DL-serine and DL-phenylalanine is decreased in aqueous dimethylsulfoxide. DL-phenylalanine is comparatively more stable than DL-serine in such protic-dipolar aprotic aqua-organic binary solvent mixture. The cavity forming, dipole–dipole and chemical interactions influence the solvation mechanism of these two amino acids. The dispersion interaction and hydrogen bonding interactions play foremost role to control solvation mechanism of these amino acids. These types of interactions are also significant for controlling amino acid induced solvent–solvent interaction which is reflected in the change in disorderness that is in transfer entropy in the mixed binary solvent.Acknowledgements
The authors record their kind thanks to the Department of Chemistry, Visva-Bharati for financial assistance and computational facilities. Authors are also pleasure to acknowledge to Shibpur Dinobundhoo Institution (college) for encouragement in this work.References
- S. Lapamje, In physico-chemical Aspects of proteins denaturation, Wiley Intercience, New York, 1978 Search PubMed.
- F. Koseoglu, E. Kilic and A. Dogan, Anal. Biochem., 2000, 277, 243–246 CrossRef CAS PubMed.
- S. Chatterjee and I. Basu mallick, J. Chin. Chem. Soc., 2007, 54, 667–672 CrossRef CAS PubMed.
- M. N. Islam and R. P. Wadi, Phys. Chem. Liq., 2001, 39, 77–84 CrossRef CAS PubMed.
- T.-S. Bani pal, G. Singh and B.-S. Lark, J. Solution Chem., 2001, 30, 657–670 CrossRef CAS.
- C. Held, T. Reschke, R. Müller, W. Kunz and G. Sadowski, J. Chem. Thermodyn., 2014, 68, 1–12 CrossRef CAS PubMed.
- J.-B. Daldrup Grosse, C. Held, G. Sadowski and G. Schembecker, Ind. Eng. Chem. Res., 2011, 50, 3503–3509 CrossRef.
- J.-B. Daldrup Grosse, C. Held, F. Ruether, G. Schembecker and G. Sadowski, Ind. Eng. Chem. Res., 2010, 49, 1395–1401 CrossRef.
- C. Held, L. F. Cameretti and G. Sadowski, Ind. Eng. Chem. Res., 2011, 50, 131–141 CrossRef CAS.
- J. Lu, X.-J. Wang, X. Yang and C.-B. Ching, J. Chem. Eng. Data, 2006, 51, 1593–1596 CrossRef CAS.
- S. Roy, K. Mahali and B. K. Dolui, J. Solution Chem., 2013, 42, 1472–1487 CrossRef CAS.
- S. C. H. pink and M. Auker, J. Phys. Chem., 1970, 74, 1742–1747 CrossRef.
- S. Roy, K. Mahali, S. Akhtar and B. K. Dolui, Asian J. Chem., 2013, 25, 6661–6665 CrossRef CAS.
- S. Roy, K. Mahali and B. K. Dolui, Asian J. Chem., 2013, 25, 8037–8042 CrossRef CAS.
- Y. Nozaki and C. Tanford, J. Biol. Chem., 1963, 238, 4074–4081 CAS.
- M. Abu- Hamd lyyah and A. Shehabuddin, J. Chem. Eng. Data, 1982, 27, 74–76 CrossRef.
- H. Talukdar, S. P. Rudra and K. K. Kundu, Can. J. Chem., 1988, 66, 461–468 CrossRef CAS.
- S. Roy, K. Mahali, M. Murmu and B. K. Dolui, Int. J. Chem. Phys. Sci., 2014, 3, 29–42 CAS.
- S. Roy, K. Mahali, S. Mondal and B. K. Dolui, Russ. J. Phys. Chem. A, 2015, 89, 654–662 CrossRef CAS.
- P. B. Undre, P. W. Khirade, V. S. Rajenimbalkar, S. N. Helambe and S. C. Mehrotra, J. Korean Chem. Soc., 2012, 56, 416–423 CrossRef CAS.
- S. Roy, K. Mahali and B. K. Dolui, BioChem.: Indian J., 2009, 3, 63–68 Search PubMed.
- S. Roy, K. Mahali and B. K. Dolui, BioChem.: Indian J., 2010, 4, 71–76 CAS.
- R. Sinha, S. K. Bhattacharya and K. K. Kundu, J. Mol. Liq., 2005, 122, 95–103 CrossRef CAS PubMed.
- J. Datta and K. K. Kundu, J. Phys. Chem., 1982, 86, 4055–4061 CrossRef CAS.
- J. Datta and K. K. Kundu, Can. J. Chem., 1983, 61, 625–631 CrossRef CAS.
- A. Bhattacharyya and S. K. Bhattacharyya, J. Solution Chem., 2013, 42, 2149–2216 CrossRef CAS.
- K. Mahali, S. Roy and B. K. Dolui, J. Biophys. Chem., 2011, 2, 185–193 CrossRef CAS.
- K. Mahali, S. Roy and B. K. Dolui, J. Solution Chem., 2013, 42, 1096–1110 CrossRef CAS.
- K. Mahali, S. Roy and B. K. Dolui, J. Chem. Eng. Data, 2015, 60, 1233–1241 CrossRef CAS.
- U. Mandal, S. Bhattacharya, K. Das and K. K. Kundu, Z. Physik. Chemic. Neue Folge, 1988, 159, 21–36 CrossRef CAS.
- A. L. Ferreira, A. E. Macedo and S. P. Pinho, Ind. Eng. Chem. Res., 2005, 44, 8892–8898 CrossRef.
- Y. Marcus, Ion Solvation, John Willy & Sons, Chicester, U. K, 1985 Search PubMed.
- J. I. Kim, A. Cocal, H. Born and E. A. Comma, Z. Physik. Chemic. Neue Folge, 1978, 110, 209–227 CrossRef CAS.
- B.-V.-K. Naidu, K.-C. Rao and M. C. S. Subha, J. Chem. Eng. Data, 2002, 47, 379–382 CrossRef CAS.
- M. I. Myhovich and V. A. Kelman, Ukr. J. Phys., 2014, 59, 581–588 CAS.
- B. Dittrich and D. Jayatilaka, Struct. Bonding, 2012, 47, 27–46 CrossRef.
- W. S. Macgregor, Ann. N. Y. Acad. Sci., 1997, 141, 3–12 CrossRef PubMed.
- G. Graziano, J. Phys. Chem. B, 2001, 105, 2632–2637 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |