Determination of the ion exchange process of K2Ti4O9 fibers at constant pH and modeling with statistical rate theory
Abstract
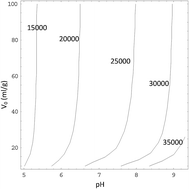
The ion exchange kinetics of K2Ti4O9 fibers at constant pH was determined precisely by ion-selective electrodes, and activity coefficients of ions in solutions were calculated by the Lu–Maurer equation. It was found that the equilibrium time and TiO2/K2O molar ratio in the solid phase are more sensitive to pH than to water volume. After that, a two-step exchange kinetics model was developed, in which a statistical rate theory base on chemical potential difference between interface was use to describe surface reaction process instead of an empirical exponential equation. The model shows that the resistance of the surface reaction step, which includes hydration of K+ ions on the surface and their transport in the solid phase, is the main resistance of the ion exchange process.

 Please wait while we load your content...
Please wait while we load your content...