Crystal structures and properties of nitrogen oxides under high pressure

Abstract

First-principles calculations were performed to investigate the structural, electronic, and elastic properties of N₂O₄ and N₂O₅. Two new phases, namely, P4₂2₁2 N₂O₄ and P2₁/m N₂O₅, are determined under high pressure through an ab initio evolutionary algorithm. For N₂O₄, the Im3 phase transforms to the P4₂2₁2 structure at 35 GPa. The pressure–volume curves of N₂O₄ and N₂O₅ show that this transition has a first-order nature. The calculated phonon dispersion and elastic constants of Im3 N₂O₄, P4₂2₁2 N₂O₄, and P2₁/m N₂O₅ demonstrate that the dynamic and mechanical stable pressure ranges are 2–35, 35–80, and 29–120 GPa, respectively. The electronic properties and projected density of states imply that these three structures are insulators. Furthermore, the N–N and N–O bond length of nitrogen oxides under high pressure are discussed.

---

1. Introduction

Various pressure-induced transformations, such as structural and electronic phase transitions, chemical reactions, and bonding patterns, in atomic and molecular systems have been studied.^1,2 Nitrogen oxides are a group of interest because they are ideal energy storage materials and exhibit complex behavior under high pressure. On the other hand, the biological and environmental chemistry properties of nitrogen oxides and their structurally characteristics are fascinating. Most special is N₂O₄, which is a planar dimer of NO₂ with a longer N–N bond than the conventional N–N single bond.³ The behavior of nitrogen oxides under high pressure has gained increased research attention over the last few decades.

Kvick et al.³ studied the cubic phase of planar N₂O₄ molecules (space group Im3) obtained from condensed gas and found that the phase remains stable at temperatures as low as 20 K. Agnew et al.⁴ reported that planar and non-cubic β-N₂O₄ can be formed through laser irradiation of cubic α-N₂O₄. At a pressure range of 1.5–3 GPa, β-N₂O₄, which is regarded as metastable, exhibits a reversible phase transition to ionic NO⁺NO₃⁻, whereas α-N₂O₄ is stable to at least 7.6 GPa.⁴ Previous studies elucidated the synthesis of aragonite-type and possible non-centrosymmetric ionic solid NO⁺NO₃⁻ from N₂O at high pressures and temperatures.⁵ Meng et al.⁶ applied hard X-ray photon radiation to induce dissociation of N₂ and O₂ molecules and generate ionic NO₂⁺NO₃⁻ at 0.5 GPa. At 1.7 GPa, these molecules subsequently decompose into ionic NO⁺NO₃⁻, whose structure was determined as layer monoclinic P2₁/m.

Sihachakr and Loubeyre⁷ found that the ionic compound synthesized from N₂/O₂ mixtures with 66% O₂ exhibits a Pmmm structure at 5.5 GPa, this structure differs from that obtained from the N₂O system for the topochemical effect. Song et al.⁸ studied N₂O₄ through Raman, synchrotron infrared, and X-ray diffraction measurements and observed a transformation from molecular to ionic structure under high P–T conditions. Kuznetsov et al. and Meng et al. presented different views about transformation of NO⁺NO₃⁻ compound to NO₂⁺NO₃⁻ crystal at temperatures higher than ambient and pressure lower than 9 GPa. A series of transformations were demonstrated (NO⁺NO₃⁻ → NO₂⁺NO₃⁻ → N₂O₄), and the spatial group of NO₂⁺NO₃⁻ was reported as hexagonal P6₃/mmc.⁹ Recently, a new orthorhombic Pna2₁ phase of NO⁺NO₃⁻ has been reported by Xiao et al.¹⁰ through theoretical studies on N₂O, the obtained phase is more stable than the monoclinic phase.

To the best of our knowledge, although several experimental studies are available, a few theoretical investigations were performed. Theoretical and experimental investigations about the structure of nitrogen oxides under high pressure have been conducted, however, their structures and mechanical properties under extremely high pressures have not been described. In this work, the thermodynamical and mechanical stability of nitrogen oxides are discussed.

2. Computational methods

In this paper, the evolutionary algorithm^11–16 which has been designed to search for the structure with the lowest free energy at high P–T condition is used to search for candidate high pressure structure. The evolutionary algorithm is performed with the USPEX code. Our first-principle calculations on N₂O₄ and N₂O₅ are performed with the Cambridge serial total energy package (CASTEP)^17,18 code using plane-wave pseudopotential method¹⁹ and employing the generalized gradient approximation functional (GGA)²⁰ of Perdew–Burke–Ernzerhof (PBE)²¹ for the exchange–correlation energy. The energy cutoff was set to 960 eV for the total energy calculations on account of convergence tests. The Monkhorst–Pack K-meshes²² were used with the resolution of 2π × 0.03 Å⁻¹ for Brillouin zone (BZ) sampling to ensure that all the enthalpy calculations were well converged to less than 0.05 meV per atom. The structure relaxation and self-consistent calculations of lattice constants and atomic position are carried out by using the Brodyden–Fletcher–Goldfarb–Shaano (BFGS) method.²³ The phonon calculations are carried out using a supercell approach²⁴ combined with linear response theory.

3. Results and discussion

3.1. Predicting structures and stability of nitrogen oxides under high pressure

Simulations of an N/O system were performed to predict the structures of the compositions of N₂O₄ and N₂O₅ at pressures lower than 120 GPa. Different types of relaxed structures were found. In accordance with the simulations, P4₂2₁2 N₂O₄ (2 f.u. per cell) at 60 GPa and P2₁/m N₂O₅ (2 f.u. per cell) at 60 GPa are presented in Fig. 1. The Im3 N₂O₄ at 20 GPa originated from experimental results at low pressure³ and is presented in Fig. 1. For Im3 N₂O₄, which was obtained from a previous study,³ one nitrogen atom is connected to two oxygen atoms and exists in the form of an NO₂ dimer, which is on the same plane. For P4₂2₁2 N₂O₄, the two nitrogen atoms are contiguous and each nitrogen atom is connected to two oxygen atoms. Interestingly, one NO₂ unit appears to spin, thereby bringing two NO₂ units out of the same plane. For P2₁/m N₂O₅, one nitrogen atom is linked with three oxygen atoms, with an oxygen atom as the center, and forms a symmetrical structure, which is apparently a layer structure. All nitrogen atoms, as well as all oxygen atoms for the last two phases, are in the same plane.

Fig. 1 The stable structures of nitrogen oxides are chose. (a) Im3 N₂O₄ at 20 GPa, (b) P4₂2₁2 N₂O₄ at 60 GPa, (c) and (d) P2₁/m N₂O₅ at 60 GPa. The yellow and green ball delegate O and N atom, respectively.

The structural thermodynamical stability was systematically studied. The formation enthalpy were calculated on new nitrogen oxide structures, namely, P4₂2₁2 N₂O₄ (2 f.u. per cell), P1 N₂O₄ (1 f.u. per cell), P1 N₂O₅ (1 f.u. per cell), and P2₁/m N₂O₅ (2 f.u. per cell), and known structures, such as Im3 (3 f.u. per cell, ref. 3), P2₁/m (2 f.u. per cell, ref. 7), and Pna2₁ (4 f.u. per cell, ref. 10) for N₂O₄, as well as P6₃/mmc (2 f.u. per cell, ref. 9) for N₂O₅. The calculated enthalpy difference curves for the new structures relative to Im3 N₂O₄ and P6₃/mmc N₂O₅ as a function of pressure are shown in Fig. 2. From Fig. 2(a), P4₂2₁2 N₂O₄ is apparently more stable than P1 N₂O₄ at high pressure and P2₁/m N₂O₅ exhibits lower enthalpy than other structures within the whole pressure range presented in Fig. 2(b). Meanwhile, Im3 N₂O₄ transforms into the P4₂2₁2 structure at 35 GPa. The calculated pressure–volume data is plotted in Fig. 2(c), which demonstrates that the volume decreases discontinuously about 2.5% with increasing pressure, thereby confirming that the phase transition is a first-order nature.

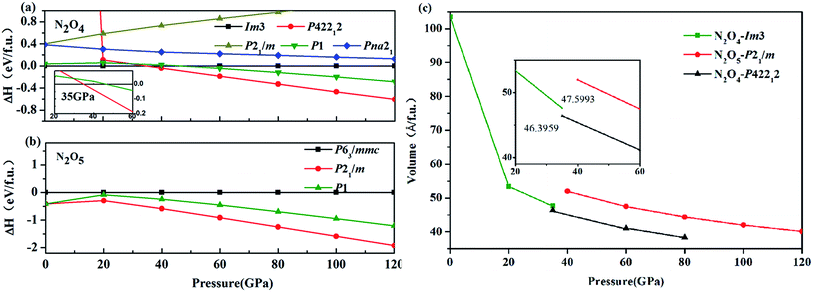Fig. 2 Thermal stability of nitrogen oxides. (a) and (b) Calculated enthalpy difference of nitrogen oxides in the pressure from 2 to 120 GPa. (c) The calculated P–V relationship for N₂O₄ and N₂O₅.

The plot of the thermodynamic convex hull shown in Fig. 3(a) indicates the thermodynamical stability of nitrogen oxides. N₂O₄ appears first at 0 GPa, N₂O₅ starts to occur under compression at 40 GPa, and both of them coexist between 40 and 80 GPa. At pressure higher than 80 GPa, the enthalpy difference changes make the formation of N₂O₄ prohibited. This finding indicates that nitrogen content decreases with increasing pressure, that is, energy storage is reduced. Formation enthalpies were calculated and are shown in Fig. 3(b) to confirm the pressure range of N₂O₄ and N₂O₅. Accordingly, N₂O₄ adopts the Im3 phase at pressure ranging from 0 to 35 GPa and the P4₂2₁2 structure stabilizes at 80 GPa. In addition, P2₁/m N₂O₅ is predominant at pressure ranging from 29 GPa to 120 GPa.

Fig. 3 (a) Convex hull curve of nitrogen oxides. (b) The formation enthalpy of N₂O₄ and N₂O₅ at pressure range from 0 to 120 GPa.

Phonon dispersion curves were constructed at 0 K to verify the dynamical stability of Im3 N₂O₄ P4₂2₁2 N₂O₄, and P2₁/m N₂O₅ at pressures (selected phonon dispersion as shown in Fig. 4(a)). No imaginary phonon frequency exists in the whole Brillouin zone. This finding confirms the dynamical stability of the three phases. In addition, phonon spectrums of Im3 N₂O₄ at 0 and 2 GPa at 0 K were calculated, which were not shown here. The phonon dispersion results show that Im3 N₂O₄ is stable in the pressure range of 2 to 35 GPa.

Fig. 4 (a) The delineative phonon dispersive curves for Im3 N₂O₄ at 20 GPa. P4₂2₁2 N₂O₄ at 60 GPa. P2₁/m N₂O₅ at 60 GPa, respectively. (b) The calculated electronic structure for Im3 N₂O₄, P4₂2₁2 N₂O₄ and P2₁/m N₂O₅ at 20, 60 and 60 GPa, respectively.

3.2. Electronic properties of nitrogen oxides

The calculated electronic energy band structure of Im3 N₂O₄, P4₂2₁2 N₂O₄, and P2₁/m N₂O₅ along high-symmetry directions in the Brillouin zone at 20, 60, and 60 GPa, respectively, are displayed in Fig. 4(b). The three structures are all insulators, as confirmed based on the underestimation of band gap caused by PBE through generalized gradient approximation.¹⁰ The variation trend of the band gap for N₂O₄ and N₂O₅ on compression is plotted in Fig. 5, which indicates that the band gap of both nitrogen oxides decrease monotonically with increasing pressure. The band gap of N₂O₅ is significantly larger than N₂O₄, but the rate of descent for N₂O₄ is faster than N₂O₅.

Fig. 5 Pressure variation of the band gap of N₂O₄ and N₂O₅.

Over the past few years, the bonding properties of nitrogen oxides have been investigated^25–33 theoretically and experimentally. In this paper, the optimized structure was obtained through density functional theory using CASTEP code with the GGA of PBE for exchange–correlation energy. Theoretical and experimental results of N₂O₄ are tabulated in Table 1, in which the distance of N–N and N–O decreases with increasing pressure. Kvick et al.³ studied the N–N and N–O bond length of N₂O₄ at various temperatures, the results showed that R_NO decreases with increasing temperature, whereas R_NN is not affected by changes in temperature. Hence, the distance of R_NO for Im3 N₂O₄ at 2 GPa is consistent with the experimental value but R_NN is higher than the experimental results and other theoretical values. N₂O₄ is a dipolymer of NO₂ bridged by N–N bond. The weak N–N bond may be explained by the electron correction effects,³ N–N antibonding pπ orbitals,³² and HOMO contributions to the N–N bond.³² For example, electron correction effects is a kind of Coulomb interaction, here the two nitrogen atoms are carrying positive charge, so a strong repulsive interaction is there. That makes the bond length between nitrogen and nitrogen is very long and the bond order is very small, so as to make the weak bonding between the two nitrogen atoms. Moreover, the HOMO of electron is antibonding orbital, this characteristic may decrease the bonding energy in molecule.

Table 1 The calculated N–N and N–O bond lengths (Å) of N₂O₄ at different pressures compared with other theoretical results and the experimental values

	Im3		P42212
	2 GPa	20 GPa	40 GPa	60 GPa	80 GPa
a Ref. 28, ground state.b Ref. 31.c Ref. 32.d Ref. 25, at 252 K.
RNN (Å)	1.835	1.705	1.683	1.626	1.581
RNO (Å)	1.199	1.188	1.185	1.180	1.175

---

	ACM^a	B3P86^b	B3PW91^b	B3LYP^c	Exp^d
RNN (Å)	1.773	1.774	1.782	1.779	1.782
RNO (Å)	1.183	1.183	1.183	1.189	1.190

---

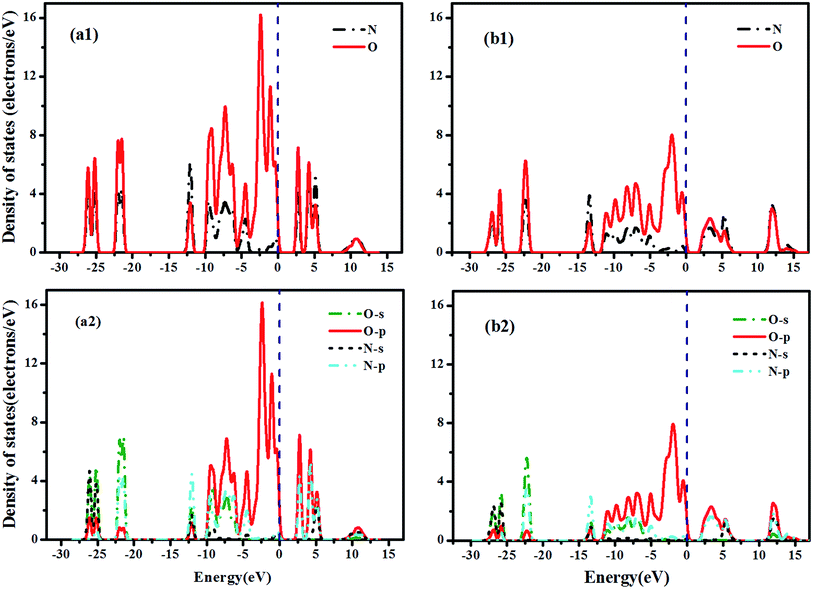
The projected density of states for Im3 N₂O₄ (20 GPa) and P4₂2₁2 N₂O₄ (60 GPa) are shown in Fig. 6. Fig. 6(a1) and (b1) show the intense hybridization of N and O atoms within the whole energy range, except −4 to 0. Moreover, the O atom is the major contributor near the Fermi surface. Fig. 6(a2) and (b2) indicate that O-p and N-p states primarily participate in the bonding. Consequently, we hypothesized that the strong interaction between N and O atoms weakens the N–N bond. A weak N–N bond is considered as an unusual covalent bond, in accordance with the results presented by Chesnut³² and Llusar et al.³³ for Im3 N₂O₄ and P4₂2₁2 N₂O₄, respectively. Table 2 presents the three mean values of the N–O bond length of P2₁/m N₂O₅ at 60 GPa as well as other theoretical and experimental values, the results reveal that P2₁/m N₂O₅ exhibits the C_2v structure. The calculated length of three different N–O bonds decreases with increasing pressure. The results we gained are in agreement with the other values in the table, such as the data of ACM, B3P86 and experiment, respectively, which are obtained from the N₂O₅ molecule. The N–O2 and N–O3 bonds contract smoothly with an overall decrease of 0.51% at 60 GPa. Similarly, the N–O1 distances decrease monotonically with a somewhat larger contraction of 1.68% reflecting the larger compressibility.

Fig. 6 The projected density of states (a) Im3 N₂O₄ at 20 GPa. (b) P4₂2₁2 N₂O₄ at 60 GPa.

Table 2 The calculated N–O bond lengths (Å) for P2₁/m N₂O₅ at different pressures compared with other theoretical results and the experimental values

	40 GPa	60 GPa	80 GPa	100 GPa	120 GPa
a Ref. 28.b Ref. 31.c Ref. 26.
RNO1 (Å)	1.490	1.465	1.445	1.428	1.418
RNO2 (Å)	1.184	1.178	1.172	1.167	1.162
RNO3 (Å)	1.183	1.177	1.172	1.167	1.162

---

	ACM^a	B3P86^b	B3PW91^b	B3LYP^b	Exp^c
RNO1 (Å)	1.495	1.494	1.496	1.512	1.498
RNO2 (Å)	1.182	1.182	1.183	1.187	1.188
RNO3 (Å)	1.183	1.184	1.184	1.188	1.188

---

3.3. Elastic properties

The elastic constants of Im3 N₂O₄, P4₂2₁2 N₂O₄, and P2₁/m N₂O₅ at 20, 60, and 80 GPa, respectively, were calculated to determine the mechanical stability of nitrogen oxides, and the results are listed in Table 3. The elastic constants C_ij calculated employing strain-stress relations at finite strains under high pressure. The elastic constants of the three phases satisfy the mechanical stability criteria, hence, these structures are mechanically stable. The well-known Born stability criteria³⁴ for cubic, tetragonal and monoclinic system are cubic phase:³⁵ C₁₁ > 0, C₄₄ > 0, C₁₁ > C₁₂, (C₁₁ + 2C₁₂) > 0.

Table 3 Elastic constants C_ij (GPa) for Im3 N₂O₄, P4₂2₁2 N₂O₄ and P2₁/m N₂O₅ at 20, 60 and 80 GPa, respectively (unit: GPa)

Im3	C11		C44		C12
	177.92		40.94		62.86
P42212	C11	C33	C44	C66	C12	C13
	385.82	377.36	113.42	112.02	171.79	200.77
P21/m	C11	C22	C33	C44	C55	C66	C12
	616.83	495.50	691.08	62.82	179.85	73.94	212.03
	C13	C15	C23	C25	C35	C46
	198.82	34.17	208.97	−1.65	−44.32	−2.72

---

Tetragonal phase³⁵. C₁₁ > 0, C₃₃ > 0, C₄₄ > 0, C₆₆ > 0, (C₁₁ − C₁₂) > 0, (C₁₁ + C₃₃ − 2C₁₃) > 0, [2(C₁₁ + C₁₂) + C₃₃ + 4C₁₃] > 0.

Monoclinic phase³⁵. C₁₁ > 0, C₂₂ > 0, C₃₃ > 0, C₄₄ > 0, C₅₅ > 0, C₆₆ > 0, [C₁₁ + C₂₂ + C₃₃ + 2(C₁₂ + C₁₃ + C₂₃)] > 0, (C₃₃C₅₅ − C₃₅²) > 0, (C₄₄C₆₆ − C₄₆²) > 0, (C₂₂ + C₃₃ − 2C₂₃) > 0, [C₂₂ (C₃₃C₅₅ − C₃₅²) + 2C₂₃C₂₅C₃₅ − C₂₃² C₅₅ − C₂₅² C₃₃] > 0, {2[C₁₅C₂₅ (C₃₃C₁₂ − C₁₃C₂₃) + C₁₅C₃₅ (C₂₂C₁₃ − C₁₂C₂₃) + C₂₅C₃₅ (C₁₁C₂₃ − C₁₂C₁₃)] − [C₁₅² (C₂₂C₃₃ − C₂₃²) + C₂₅² (C₁₁C₃₃ − C₁₃²) + C₃₅² (C₁₁C₂₂ − C₁₂²)] + C₅₅g} > 0. g = C₁₁C₂₂C₃₃ – C₁₁C₂₃² – C₂₂C₁₃² – C₃₃C₁₂² + 2C₁₂C₁₃C₂₃.

Furthermore, the calculated pressure dependencies of normalized lattice constants such as a/a₀, b/b₀, and c/c₀ from 0 to 120 GPa for P2₁/m N₂O₅ are illustrated in Fig. 7, where a₀, b₀, and c₀ are the values under ambient condition. The compression of this structure is regarded as anisotropic, with low compressibility along the c-axis and high compressibility along the b-direction, which could be due to the weak force among the layers. The simulation results of elastic constants (Table 3) show that C₃₃ is higher than C₁₁ and C₂₂. Hence, P2₁/m N₂O₅ is the most incompressible along the c-axis; this finding is consistent with the normalized lattice constants calculated.

Fig. 7 Calculated the normalized lattice constants for P2₁/m N₂O₅ as a function of pressure.

4. Conclusions

In summary, the properties of nitrogen oxides, namely, P4₂2₁2 N₂O₄ and P2₁/m N₂O₅, under high pressure are revealed through ab initio evolutionary simulations. Im3 N₂O₄ changes to P4₂2₁2 N₂O₄ at 35 GPa, and this phase transition is determined to be a first-order reaction, as evidenced by the discontinuous decrease in volume. The convex hull diagram indicates that P4₂2₁2 N₂O₄ and P2₁/m N₂O₅ coexist from 29 GPa to 80 GPa. N₂O₄ adopts Im3, P4₂2₁2, and P2₁/m N₂O₅ within pressure ranges of 2–35, 35–80, and 29–120 GPa, respectively. The phonon dispersion diagrams and elastic constants suggest that the three structures are dynamically and mechanically stable. Meanwhile, the calculated electronic energy bands confirm that these three structures are insulators. We can find that there are no electronic energy bands through the Fermi surface. That confirms both N₂O₄ and N₂O₅ are insulator. Meanwhile, the density of states is 0 (electrons per eV) at Fermi level showed in Fig. 6 reveals the same electronic property. The elastic constants calculated also confirm that P2₁/m N₂O₅ is the most incompressible along the c-axis, whereas the calculated bond lengths suggest that the N–N bond is an unusual covalent bond.

Acknowledgements

This work was supported by the National Basic Research Program of China (No. 2011CB808200), National Natural Science Foundation of China (No. 51572108, 11574109, 11404134, and 11074090), Program for Changjiang Scholars and Innovative Research Team in University (No. IRT1132), National Found for Fostering Talents of basic Science (No. J1103202), and Specialized Research Fund for the Doctoral Program of Higher Education (20120061120008 and 20110061120007), Parts of calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.

References

1. R. J. Hemley, Annu. Rev. Phys. Chem., 2000, 51, 763–800.
2. J. Sun, D. D. Klug, C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2011, 106, 145502.
3. A. Kvick, R. K. McMullan and M. D. Newton, J. Chem. Phys., 1982, 76, 3754–3761.
4. S. F. Agnew, B. I. Swanson, L. H. Jones, R. L. Mills and D. Schiferl, J. Phys. Chem., 1983, 87, 5065–5068.
5. S. Maddury, A. Madduri, A. F. Goncharov, O. Tschauner, P. F. McMillan, H. R. Mao and R. J. Hemley, Phys. Rev. Lett., 2011, 87, 135504.
6. Y. Meng, R. B. Von Dreele, B. H. Toby, P. Chow, M. Y. Hu, G. Y. Shen and H. K. Mao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 214107.
7. D. Sihachakr and P. Loubeyre, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 064113.
8. Y. Song, R. J. Hemley, H. K. Mao, Z. X. Liu and D. R. Herschbach, Chem. Phys. Lett., 2003, 382, 686–692.
9. Y. Kuznetsov, L. Dubrovinsky, A. Kurnosov, M. M. Lucchese, W. Crichton and C. A. Achete, Adv. Phys. Chem., 2009, 2009, 180784.
10. H. Xiao, Q. An, W. A. Goddard, W. G. Liu and S. V. Zybin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 5321–5325.
11. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704–244715.
12. C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720.
13. R. Oganov, C. W. Glass and S. Ono, Earth Planet. Sci. Lett., 2006, 241, 95–103.
14. O. Lyakhov, A. R. Oganov and M. Valle, Comput. Phys. Commun., 2010, 181, 1623–1632.
15. A. R. Oganov, A. O Lyakhov and M. Vallen, Acc. Chem. Res., 2011, 44, 227–237.
16. A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182.
17. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
18. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
19. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
21. B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413.
22. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
23. R. H. Byrd and J. Nocedal, SIAM J. Numer. Anal., 1989, 26, 727–739.
24. K. Parlinski, Z. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066.
25. B. W. McClemlland, G. Gundersen and K. J. Hedberg, J. Chem. Phys., 1972, 56, 4541.
26. B. W. McClemlland, L. Hedberg, K. Hedberg and K. Hagen, J. Am. Chem. Soc., 1983, 105, 3789–3793.
27. A. Stirling, L. Papal, J. Mink and D. R. Salahub, J. Chem. Phys., 1994, 100, 2910.
28. H. Munakata, T. Kakumoto and J. Baker, J. Mol. Struct., 1997, 391, 231–240.
29. S. S. Wesolowski, J. T. Fermann, T. D. Crawford and H. F. Schaefer, J. Chem. Phys., 1997, 106, 7178.
30. K. B. Borisenko, M. Kolonits, B. Rozsondai and I. Hargittai, J. Mol. Struct., 1997, 413, 121–131.
31. P. Aplincourt, F. Bohr and M. F. Ruiz-Lopez, J. Mol. Struct., 1998, 426, 95–104.
32. D. B. Chesnut and A. L. Crumbliss, Chem. Phys., 2005, 315, 53–58.
33. R. Llusar, A. Beltran, J. Andres, S. Noury and B. Silvi, J. Comput. Chem., 1999, 20, 1517–1526.
34. M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1956.
35. Z. J. Wu, E. J. Zhao, H. P. Xiang, X. F. Hao, X. J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.

---