Compressed sodalite-like MgH6 as a potential high-temperature superconductor

Abstract

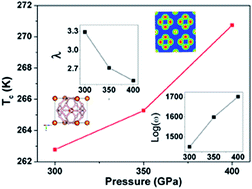
Recently, an experimental work reported a very high T_c of ∼190 K in hydrogen sulphide (H₂S) at 200 GPa. The search for new superconductors with high superconducting critical temperatures in hydrogen-dominated materials has attracted significant attention. Here we predict a candidate phase of MgH₆ with a sodalite-like framework in conjunction with first-principles electronic structure calculations. The calculated formation enthalpy suggests that it is thermodynamically stable above 263 GPa relative to MgH₂ and solid hydrogen (H₂). Moreover, the absence of imaginary frequency in phonon calculations implies that this MgH₆ structure is dynamically stable. Furthermore, our electron–phonon coupling calculation based on BCS theory indicates that this MgH₆ phase is a conventional superconductor with a high superconducting critical temperature of ∼260 K under high pressure, which is even higher than that of the recently reported compressed H₂S. The present results offer insight in understanding and designing new high-temperature superconductors.