DOI:
10.1039/C5RA11428D
(Paper)
RSC Adv., 2015,
5, 64918-64924
Manipulation and precise control of colloidal microsphere resonators coupled to a non-planar waveguide
Received
15th June 2015
, Accepted 23rd July 2015
First published on 23rd July 2015
Abstract
A new operation scheme using optoelectronic tweezers and a locally confined dielectrophoresis to implement a tunable microsphere resonator coupled to a non-planar waveguide is presented. The optoelectronic tweezers are utilized to bring the microsphere to the waveguide while the dielectrophoretic force around the waveguide is exploited to finely tune the gap space between the microsphere and the waveguide in a liquid medium. Through these two mechanisms, we demonstrate a polyester microsphere can be freely moved to an SU-8 rib waveguide and operated in any of the coupling conditions by adjusting applied voltage.
1. Introduction
Microsphere resonators are widely applied in various fields, including molecule spectroscopy, label free detection for biosensing,1 and many optical functions such as switching, multiplexing,2 nonlinear optics,3,4 etc. Inside the microsphere resonators, light could propagate along the spherical surface via total internal reflection to have a round-trip constructive interference for certain particular wavelengths, which are also known as whispering gallery modes (WGMs). WGM has the advantage of a high quality factor and a small mode volume. However, for a colloidal microsphere resonator in a liquid medium, to excite the WGM and probe the signal is challenging. The key point is whether there is a manipulation platform to precisely control the position of a suspended microsphere resonator with respect to an optical waveguide in liquid. Optical tweezers5 are commonly applied for moving colloidal objects and are already demonstrated to maneuver polystyrene microspheres (PSM) to a planar optical component.6 However, to couple the PSM to a non-planar waveguide via optical tweezers, freely and precisely controlling the position of PSM could be difficult because of a strong light scattering around this waveguide structure which may further disturb the optical trapping force originating from the optical tweezers.
In this study, we propose using optoelectronic tweezers (OET) and a locally confined dielectrophoresis (LCDEP) to precisely control the relative position of a PSM coupled to a rib waveguide in a liquid medium. OET7 have been reported to be an ideal tool for manipulating colloidal objects freely just via a simple optical projection setup. Nevertheless, the movement is mainly on the horizontal plane and the resolution is ultimately limited by the pixel size of the projector. Therefore, we take advantage of LCDEP generated around the waveguide itself to align the PSM exactly on the top. Furthermore, by tuning an applied voltage, the coupling gap between the PSM and the waveguide is adjustable and the resolution can be down to sub-micron. In combination with these two mechanisms, the PSM can be freely moved from any location to the waveguide by OET and precisely positioned through LCDEP.
2. Principles
In this section, we illustrate the basic mechanism of lightwave coupling between a microsphere resonator and waveguide, and the calculation of DEP force acting on the microsphere. The detailed description of device analysis is given in Section 3. The experimental setup and results are shown in Section 4 and 5.
2.1. Spherical whispering gallery modes
Unlike conventional standing-wave microresonators such as Fabry Perot etalons and distributed Bragg reflector cavities, the microsphere actually features as a travelling-wave resonator that has a particular resonant mode name, called WGM. Here, we assume a dielectric microsphere with a homogeneous refraction index ns and a radius R0 placed in a liquid medium that has a lower refraction index n0. A general expression of the normalized electrical field of WGM can be written by a product of three independent spatial functions in a spherical coordinate system, which are given by8,9| |
 | (1) |
where l, m and n are the mode indices with respect to the radius, inclination and azimuth coordinates, respectively, J is the spherical Bessel functions, H is the Hermite–Gauss functions, and αs is the decay constant outside the microsphere along the radial direction. The mode indices can be obtained by solving the following characteristic equation for the TM modes:| |
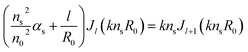 | (2) |
Note that the mode index l is directly correlated with the decay constant αs, which affects the mode coupling between the microsphere and the waveguide.
2.2. Optical transfer function of a waveguide coupled to a microsphere resonator
For a single waveguide coupled to a microsphere resonator illustrated in Fig. 1, there are two characteristic numbers governing wavelength-dependent waveguide transmittance; one is the intrinsic (or unload) quality factor Qint, and the other is the external quality factor Qext, both of which are corresponding to the power dissipation of the stored energy in the resonator and are expressed by| |
 | (3) |
| |
 | (4) |
where ω0 and βl are the angular frequency and the propagation constant of a WGM, respectively. The Gamma value is associated with the radiation loss, the scattering loss due to surface roughness and the material absorption of the microsphere that mainly depends on the wavelength. On the other hand, the Kappa value is correlated with the mode coupling between the waveguide and the resonator, which is determined by the mode field overlap integral of these two optical modes and the index perturbation seen either by the waveguide or the resonator alone. Therefore, the Kappa value varies significantly with the distance between these two components. The total quality factor, thus, is given by| | |
1/Q = 1/Qint + 1/Qext
| (5) |
by comparing Qint and Qext at resonance wavelength, three coupling conditions are defined. The first is under-coupling (Qext > Qint), where the intrinsic quality factor dominates the total quality factor. This coupling regime is typically applied for a low-threshold optical pump laser.10 The second is critical coupling (Qext = Qint), where the intrinsic quality factor is equal to the external. Under this condition, the waveguide power is completely transferred to the resonator. Zero power transmits at the output of the waveguide, and the resonator has the maximal optical energy stored inside. It has been widely exploited especially for nonlinear optics3 and sensing.11 The third is over-coupling (Qext < Qint), where the external quality factor dominates. In this case, the waveguide power is first coupled into the resonator and then coupled back to the waveguide to yield a phase difference. This resonance-induced phase difference is often utilized for implementing an optical all-pass filter.12,13 In fact, all these three coupling conditions can be characterized by a waveguide transfer function, which is formulated by:14| |
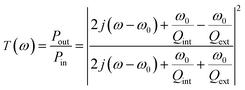 | (6) |
 |
| | Fig. 1 Schematic illustration of evanescent coupling between a microsphere resonator and a waveguide. | |
2.3. DEP force working on objects
DEP force is widely applied for moving objects dispersed in liquid through a locally non-uniform electric field. The Clausius–Mossotti function15 is usually accurate enough to find the time averaged DEP force on a small object if the depolarization of the object does not disturb the global field significantly. However, the electric field at the vicinity of a large object could be very different than the global field. In this case, the Maxwell stress tensor should be included to consider the local field and precisely calculate the DEP force on the object with any kind of shape. The Maxwell stress tensor is formulated according to a three dimensional time-averaged electrical field in space, which is given by16| |
 | (7) |
where Ei, i = x, y, z is the time-averaged local electrical field in the Cartesian coordinates. Then the net DEP force acting on the object can be obtained through integration of the tensor element all around the object surface, which is given by| |
 | (8) |
where a is the surface area of the object.
3. Operating procedure and device design
A schematic illustration of this device structure is shown in Fig. 2(a). A PSM of a 100 μm diameter is dispensed into a liquid chamber filled with a 5% sucrose solution, where the concentration of the sucrose solution is 1.01 g cm−3. Note that the sucrose solution utilized in this study is to finely engineer the gravity of the microsphere in liquid, in order to match the DEP force easily during operation. The liquid chamber is made of two transparent conducting plates separated by a 240 μm plastic double-side tape. The bottom plate consists of 1 μm indium tin oxide (ITO, n = 1.7), 1.5 μm silicon dioxide (SiO2, n = 1.45) and a rib waveguide made by SU8 (SU-8 2000 series, MicroChem, n = 1.58) stacking on a glass substrate. The top plate is laminated by 1 μm hydrogenated amorphous silicon (a:Si–H, n = 3.45) on a FTO-coated (SnO2:F) glass. The two plates are biased with an AC voltage. A commercial projector controlled by a computer creates an image pattern projected on the photoconductive amorphous silicon layer for generating a pseudo electrode. This electrode is image-controlled and yields a programmable DEP force to actuate the microsphere laterally in the chamber. A complete design and analysis on the waveguide dimension, mode coupling and the DEP force are given in the following sections.
 |
| | Fig. 2 Schematic illustration of the operating procedure (not in scale): (a) dispensing PSMs randomly in the liquid chamber, (b) selecting and moving a PSM toward the waveguide by OET, (c) attracting and aligning the PSM with the waveguide center by LCDEP, and (d) controlling the gap space between the PSM and the waveguide through adjusting the applied voltage. | |
3.1. Operating procedure
Manipulation of the microsphere resonator coupled to the waveguide is described as follow. Initially, the PSMs stay on the bottom plate until a voltage is applied to slightly lift the PSMs up without contacting the plate. Then an image is focused on the top photoconductive plate to drift the PSMs by OET, where only one PSM is selected to actuate toward the waveguide. As the PSM approaches to the rib waveguide, a non-uniform electric field around the rib generates a LCDEP force that attracts the PSM and positions it at the center of waveguide, even when the illumination is still turned on. Finally, the gap space between the rib and the PSM is finely adjusted through tuning the applied voltage. A comprehensive description of operation is shown in Fig. 2. Note that this PSM afterward can be simply moved away from the waveguide by the OET with a much higher applied voltage, because the balance position becomes far above the waveguide, resulting in a weak confinement effect by the LCDEP.
3.2. Single-mode waveguide design
The SU-8 rib waveguide should be single-mode guided to effectively excite the WGM of the microsphere resonator. Suppose the waveguide width is around 4 μm and the total waveguide height is 3.5 μm, where the thickness is based on the data sheet of SU-8 thickness provided by the company. Next, we determine the rib height and slab thickness via an empirical formula17 for the single-mode guiding condition and figure out the dimensions to be 1.4 μm and 2.1 μm, respectively. We further verify the supported mode number numerically (RF module, COMSOL multiphysics software) and confirm it is a single-mode rib waveguide. Moreover, the bottom-cladding layer of SiO2 should be thick enough to minimize the waveguide attenuation caused by ITO absorption. Analyzed by beam propagation method (Rsoft, synopsys), the minimum thickness of the SiO2 layer is 1.5 μm.
3.3. Coupling gap
To estimate the distance between the SU8 waveguide and the PSM required for essential coupling, the fundamental WGM profile and the corresponding propagation constant have to be known first. Solving the eigenmodes of an axisymmetric resonator in a cylindrical coordinate system can be converted into a two-dimensional problem.18 We use the COMSOL PDE module to analyze the WGM of the 100 μm PSM.
The coupling condition of the microsphere resonator can be examined by the value of Qint − Qext, which is a function of the gap space and the round-trip loss of the WGM. Assume the PSM has a perfect spherical shape and a smooth surface; therefore, the intrinsic quality factor Qint can be considered as a small constant, so the coupling condition is mainly dictated by the external quality factor Qext. Using eqn (2), (4) and the above simulation results, we calculate the external quality factor varied by the gap space and the result is shown in Fig. 3. The external quality factor is generally an exponential function of the gap. According to the previously reported data,17 if the intrinsic quality factor of a 100 μm PSM is typically around 1 × 104 to 5 × 106, the gap space, therefore, should be in the range of 100–400 nm to achieve the critical coupling condition.
 |
| | Fig. 3 Calculated external quality factor varied by the gap space between a 100 μm PSM and a SU-8 waveguide. | |
3.4. Calculation of DEP force
Both the OET and LCDEP forces are dependent on the local electric field on the object and the surrounding medium. For a microsphere suspended between two parallel electrode plates as an example, the induced DEP force, in light of the electric field, can be evaluated through the Maxwell stress tensor analysis.19,20 At the central level of the two plates, the DEP force is zero because of a symmetric electric field profile. However, as the object deviates from the center, it can be either attracted or expelled by the electrode, depending on the dielectric contrast between the object and the surrounding medium. This force can be very large especially when the object is close to the electrode. In our case, the dielectric constant of the PSM is smaller than that of the sucrose solution. Therefore, a negative DEP force exhibits near the surface of the bottom electrode, causing the PSM to levitate if this DEP force is strong enough to overcome the gravity.
Table 1 lists the material properties required to simulate the electric field for finding the DEP force working on the device. The separation distance of the two electrode plates, the size of the PSM and the dimension of waveguide are illustrated in Fig. 1. Here we use COMSOL AC/DC module at 100 kHz to simulate the time averaged electrical field first, and then apply eqn (7) and (8) to calculate the net DEP force on the PSM. The first study is to analyze the DEP force under light illumination (OET), where the PSM is positioned on a planar waveguide slab without the rib. A circular image pattern with a diameter of 500 μm is projected on the top photoconductive plate. Since the PSM has a slightly large density compared with the surrounding medium, we consider the DEP force with respect to the position of the PSM near the bottom plate only. The result is shown in Fig. 4. Fig. 4(b) displays the horizontal component of the generated DEP force. Near the illuminated region, the PSM suffers from a repulsive force. On the other hand, the vertical DEP force tends to push the PSM upward, especially when the PSM is close to the surface of the bottom plate (Fig. 4(c)). With combination of these two forces, the PSM can be easily moved around the bottom plate through the OET without counteracting with the contact friction. Next we study the LCDEP force in the vicinity of the rib waveguide without light illumination. Fig. 5(b) and (c) show the horizontal and vertical component of the LCDEP force, respectively, revealing that the PSM is able to be attracted and confined at the center of the waveguide horizontally while is pushed upward along the vertical direction, which is similar to the result of OET.
Table 1 Material properties utilized in the simulation
| Material |
ε (F m−1) |
σ (S m−1) |
Refractive index |
| a-Si–H |
11.8ε0 |
Light: 10−4, dark: 10−5 |
3.38 |
| SiO2 |
3.9ε0 |
1 × 10−10 |
1.45 |
| SU8 |
3.2ε0 |
1 × 10−12 |
1.56 |
| Sucrose solution |
78ε0 |
1 × 10−5 |
1.34 |
| PSM |
2.6ε0 |
4 × 10−5 |
1.57 |
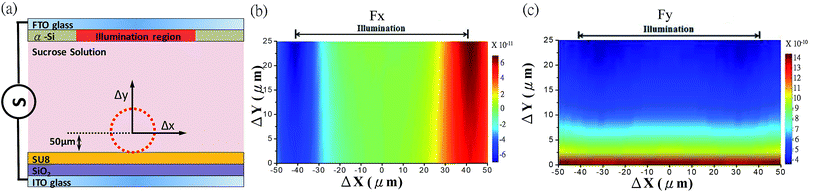 |
| | Fig. 4 Simulated DEP force with respect to the position of a 100 μm PSM under light illumination in a sucrose solution: (a) schematic illustration, (b and c) are the horizontal and vertical force field, respectively. | |
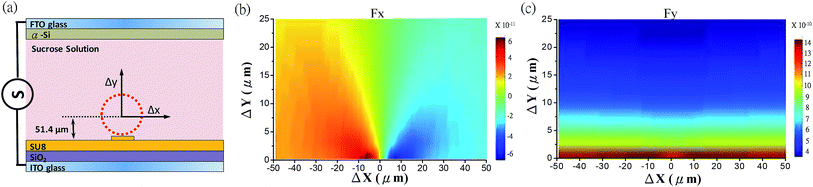 |
| | Fig. 5 Simulated DEP force with respect to the position of a 100 μm PSM near the waveguide in a sucrose solution: (a) schematic illustration, (b and c) are the horizontal and vertical force field, respectively. | |
As the PSM is confined at the center of the rib waveguide, the upward LCDEP force is against the gravity of the PSM. Because the vertical DEP force decays rapidly from the surface and is proportional to the applied voltage, at a certain altitude, these two forces are balanced and the PSM stays steadily at that position. We plot the DEP forces as functions of the gap space with respect to different applied voltages. The result is shown in Fig. 6. The intersection points of the DEP force and the gravity correspond to the balance positions of the PSM. In principle, the coupling condition of the PSM resonator can be freely controlled through tuning the applied voltage.
 |
| | Fig. 6 Simulated DEP force acting on the PSM (upward direction) versus the gap space for different applied voltages from 5.6 Vpp to 5.8 Vpp. The dash line in this diagram is the net gravity force in a sucrose solution (downward direction). | |
4. System setup
The detail of experimental setup is shown in Fig 7. An AC voltage (100 kHz sinusoidal wave) is amplified and applied across the top and bottom plate. A programmable image is projected and focused on the top photoconductive layer (a-Si) to dynamically move the PSM by the OET toward the SU-8 waveguide. A CCD camera captures the microsphere image for real-time monitoring the position of the PSM. To access the waveguide signal interacting with the microsphere resonator, an amplified spontaneous emission (AQ4315A, Ando) light source from 1530 nm to 1560 nm is launched into the SU-8 waveguide through a lensed fiber. The polarization is adjusted to be TM-polarized via an in-line linear polarizer as well as a polarization rotator. The output signal is collected by another lensed fiber connected with an optical spectrum analyzer (AQ6317B, Ando).
 |
| | Fig. 7 Illustration of the experimental setup for the PSM measurement. | |
5. Experimental results
5.1. PSM manipulation
Fig. 8 shows microscopy snapshots of manipulating a PSM to the SU-8 waveguide. The PSM is initially away from the waveguide and then driven by OET toward the waveguide through a programmable illuminated circular pattern, as displayed in Fig. 8(a)–(c). Note that in addition to DEP, light-induced ac electroosmosis and electrothermal flow can also introduce forces on the PSM.21,22 However, in this study, the operating frequency is above 100 kHz, which can exclude the effect from electroosmosis.21 As the PSM is close to the waveguide, it is attracted and positioned right at top of the waveguide via the LCDEP force introduced by the waveguide rib (Fig. 8(d)). Finally, the gap space between the PSM and the waveguide is finely adjusted by increasing the applied voltage from 60 Vpp to 120 Vpp, where the PSM is slightly pushed upward, resulting in a blurred image seen in Fig. 8(e) and (f). The applied voltage is generally much higher than the simulation value because of impedance mismatch due to a large contact resistance and capacitance between the two parallel plates.
 |
| | Fig. 8 Snapshots of manipulating the PSM via the OET and LCDEP near the waveguide rib. Because the CCD camera is not completely perpendicular to the sample surface, the PSM image is slightly deviated from the center of the waveguide during operation. Scale bar in figures are 200 μm. | |
5.2. Tunable coupling condition
Fig. 9 shows transmittance spectra of a waveguide coupled to a PSM at different applied voltages. Near 100 Vpp, a transmission dip emerges, revealing that the waveguide is properly coupled to the PSM to excite the WGM. By examining the variation of spectrum, the transmission depth, in fact, increases first and then decreases as the applied voltage alters from 95 Vpp to 110 Vpp. It indicates that the coupling condition transits from over-coupling to under-coupling, since the gap space between the PSM and waveguide increases with the applied voltage.
 |
| | Fig. 9 Measured transmittance spectra of a waveguide coupled to a PSM at different applied voltages. The coupling condition changes from over-coupling to under-coupling from 95 Vpp to 115 Vpp. The curve for 100 Vpp has the largest dip on the spectrum, indicating that it is near the critical coupling condition. | |
We also characterize Qint and Qext through fitting the experimental transmittance spectra into eqn (6) and the results are shown in Table 2. Note that the intrinsic quality factor Qint is assumed to be a fix value because it only depends on the intrinsic loss of PSM. The external quality factor Qext, however, increases with the coupling distance. As the applied voltage is below 100 Vpp, where Qext < Qint, the PSM is operated in the over-coupling regime. On the other hand, as the voltage is over 105 Vpp, it is operated in the under-coupling regime since Qext > Qint. The critical coupling ought to happen between 100 Vpp and 105 Vpp. The black curve in Fig. 9 shows the waveguide and the PSM are totally decoupled for the voltage more than 115 Vpp.
Table 2 Calculated intrinsic quality factor and external quality factors via a curve fitting technique, according to the measured transmittance spectra shown in Fig. 9
| Vpp |
Qext |
Qint |
Qtot |
Coupling condition |
| 95 |
3434 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
3043 |
Over-coupling |
| 97 |
4099 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
3554 |
Over-coupling |
| 100 |
4197 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
3627 |
Over-coupling |
| 105 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 324 |
Under-coupling |
| 110 |
49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783 783 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382 382 |
Under-coupling |
6. Conclusions
We demonstrated a platform of manipulating a colloidal microsphere resonator coupled to a non-planar waveguide. Firstly, the microsphere is brought to the vicinity of waveguide from an arbitrary location in a liquid medium via OET. Then, the LCDEP, generated by the waveguide itself, attracts and confines the microsphere exactly above the center of waveguide. Finally, the coupling distance (gap space) between the microsphere and waveguide is finely tuned by adjusting the applied voltage. In this study, a 100 μm polyester bead dispensed in a sucrose solution is utilized as the microsphere resonator. The operation chamber is made by two electrode plates separated by 180 μm; one is coated with amorphous Si for OET operation and the other is fabricated with a SU-8 waveguide structure on the surface for creating LCDEP and light coupling. Through a proper design and analysis on the waveguide dimension and the DEP force, the microsphere resonator can be freely operated from the under-coupling to over-coupling condition. This platform can be an ideal tool for studying resonance-enhanced optofluidics and all types of biological and chemical sensors.
Acknowledgements
This research work is funded by Ministry of Science and Technology (NSC100-2628-E-007-027-MY3 and MOST 103-2633-M-007-001) in Taiwan. We thanks for Prof. Gwo-Bin Lee's group in National Tsing Hua University for discussion and experimental setup.
Notes and references
- F. Vollmer and S. Arnold, Nat. Methods, 2008, 5, 591–596 CrossRef CAS PubMed.
- H. C. Tapalian, J. P. Laine and P. A. Lane, IEEE Photonics Technol. Lett., 2002, 14, 1118–1120 CrossRef.
- A. C. Turner, M. A. Foster, A. L. Gaeta and M. Lipson, Opt. Express, 2008, 16, 4881–4887 CrossRef.
- S. X. Qian, J. B. Snow and R. K. Chang, Opt. Lett., 1985, 10, 499–501 CrossRef CAS.
- S. M. Block, L. S. B. Goldstein and B. J. Schnapp, Nature, 1990, 348, 348–352 CrossRef CAS PubMed.
- J. Lutti, W. Langbein and P. Borri, Appl. Phys. Lett., 2007, 91, 141116 CrossRef PubMed.
- M. C. Wu, Proc. SPIE, 2011, 5, 324 Search PubMed.
- J. C. Knight, N. Dnbreuil, V. Sandoghdar, J. Hare, V. Lefevreseguin, J. M. Raimond and S. Haroche, Opt. Lett., 1995, 20, 1515–1517 CrossRef CAS.
- B. E. Little, J. P. Laine and H. A. Haus, J. Lightwave Technol., 1999, 17, 704–715 CrossRef.
- L. N. He, S. K. Ozdemir and L. Yang, Laser Photonics Rev., 2013, 7, 60–82 CrossRef CAS PubMed.
- M. D. Barnes, K. C. Ng, W. B. Whitten and J. M. Ramsey, Anal. Chem., 1993, 65, 2360–2365 CrossRef CAS.
- F. N. Xia, M. Rooks, L. Sekaric and Y. Vlasov, Opt. Express, 2007, 15, 11934–11941 CrossRef.
- Q. Li, M. Soltani, S. Yegnanarayanan and A. Adibi, Opt. Express, 2009, 17, 2247–2254 CrossRef CAS.
- M. Soltani, S. Yegnanarayanan, Q. Li and A. Adibi, IEEE J. Quantum Electron., 2010, 46, 1158–1169 CrossRef CAS.
- P. Y. Chiou, A. T. Ohta and M. C. Wu, Nature, 2005, 436, 370–372 CrossRef CAS PubMed.
- D. Graffiths, Introduction to Electrodynamics 3rd, 1998 Search PubMed.
- R. A. Soref, J. Schmidtchen and K. Petermann, IEEE J. Quantum Electron., 1991, 27, 1974 CrossRef.
- M. Oxborrow, IEEE Trans. Microwave Theory Tech., 2007, 55, 1209–1218 CrossRef.
- T. S. Santra and F. G. Tseng, Micromachines, 2013, 4, 333–356 CrossRef PubMed.
- N. Green and H. Nili, Encyclopedia of Nanotechnology, 2012, pp. 534–543 Search PubMed.
- J. K. Valley, A. Jamshidi, A. T. Ohta, H. Y. Hsu and M. C. Wu, J. Microelectromech. Syst., 2008, 17, 342–350 CrossRef CAS PubMed.
- A. Kumar, S. J. Williams, H. S. Chuang, N. G. Green and S. T. Wereley, Lab Chip, 2011, 11, 2135–2148 RSC.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 
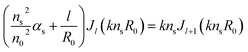


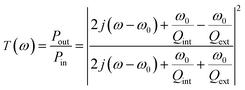




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311
311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324
324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 783
783![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707
707![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 382
382






