Structure and oxide ion conductivity in tetragonal tungsten bronze BaBiNb₅O₁₅

Abstract

The crystal structure and electrical properties of a tetragonal tungsten bronze (TTB) compound, BaBiNb₅O₁₅, were investigated by high-resolution synchrotron X-ray powder diffraction and AC impedance spectroscopy. The compound is a new type of oxide ion conductor with a total electrical conductivity of 3 × 10⁻⁴ S cm⁻¹ at 600 °C and a relatively small activation energy (0.3–0.5 eV). It is suggested that the large amount of cationic vacancies in the A sites, the large free space created by the large Ba²⁺ cations, and the splits of the Bi atoms are in favor of oxygen ion migration. This stable tungsten bronze compound BaBiNb₅O₁₅ with moderate oxide ion conductivity shows potential for applications in SOFC anodes, amperometric gas sensors, and active catalyst supports.

---

1. Introduction

Tetragonal tungsten bronze (TTB) type materials are a big family of functional compounds that are composed of layered corners sharing an octahedra framework. The general formula of TTB-type structures can be formulated as (A2)₄(A1)₂(C)₄(B1)₂(B2)₈O₃₀, where A1, A2, and A3 are quadrangular (12-coordinated), pentagonal (15-coordinated), and triangular (9-coordinated) tunnels, respectively.¹ B1 and B2 are the octahedral sites. In general, the A1 and A2 sites can be fully or partially occupied by larger cations such as alkaline, alkaline earth, rare earth, bismuth or lead,² whereas the smaller A3 sites can be filled with very small ions such as Li⁺ ions but are more typically vacant (see Fig. S1 in ESI†).³ The structures and dielectric properties of these materials have been widely investigated due to their instinct crystalline sites and compositional flexibility.^4–10

Oxide materials that exhibit oxygen ion conductivity have attracted a great deal of interest due to their wide applications such as oxygen separation membranes, gas sensors, catalysts, and electrodes and electrolytes for solid-oxide fuel cells (SOFCs).^11–14 One such family of oxides that has been widely studied is those with a perovskite structure. Herein, for example, (Sr,Mg)-doped LaGaO₃ shows a higher ionic conductivity than conventional zirconia-based electrolytes such as YSZ at moderate temperatures,¹⁵ whereas mixed ionic-electronic conductors, such as doped La_1−xSr_xMnO₃ and La_1−xSr_xCoO₃, are widely used as cathode materials in SOFCs.¹⁶ Computer simulations have shown that the oxygen ion migration occurs by a hopping mechanism between adjacent oxygen sites along a BO₆ octahedron edge with a slightly curved trajectory accompanied by outward relaxation of the adjacent cations,^17,18 and the migrating ion moves through the center of a triangle (or saddle-point) defined by two A site cations and one B site cation.^19,20 As is known, TTB-structured compounds possess a similar network of corner-sharing BO₆ octahedra (with similar saddle-points in a lattice). Moreover, the larger pentagonal tunnels and vacancies (cationic vacancies) in the A1 and A2 sites may provide more free space for the migration of oxygen ions and minimize the migration energy. However, few reports have addressed the oxide ion conductivity concerning TTB oxides. Kaiser et al. investigated (Ba/Sr)₃Nb₄TiO₁₅ as an anode material for SOFCs, which revealed respectable conductivities (∼10 S cm⁻¹ at 930 °C) under reducing conditions; however, it suffered from poor oxygen ion conductivity.²¹ Similarly, Prades et al.²² investigated the electrical properties of oxygen-deficient TTB ceramics Ba₂NdTi_2+xNb_3−xO_15−x/2, in which only a small number of oxygen vacancies and low oxide ion conduction could be obtained by varying the Ti/Nb ratio. More recently, Kuang et al. studied nonstoichiometric TTB-type compounds Ba_0.5−xTaO_3−x; nevertheless, the highly nonstoichiometric (TaO)³⁺-containing phase exhibited a migration of Ba²⁺ cations rather than of oxygen ions.²³

In this study, we report a Bi-based TTB-type oxide, BaBiNb₅O₁₅ (BBN). It is a stable oxygen ion conductor with an electrical conductivity of ∼3 × 10⁻⁴ S cm⁻¹ at 600 °C, which is much larger than any of the other reported TTB compounds, and may have potential applications in SOFC anodes, amperometric gas sensors and active catalyst supports.¹² The structure of BBN was characterized by high-resolution synchrotron X-ray powder diffraction (SPD). The electrical properties were measured by AC impedance spectroscopy. Two other compounds, Ba₂BiNb₃Ti₂O₁₅ (BBNT) and SrBiNb₅O₁₅ (SBN), were also synthesized for comparison. This study shows that TTB-type compounds may be a new family of oxygen ion conducting materials.

2. Experimental

BBN ceramics were synthesized by a solid-state method using BaCO₃ (99%), Nb₂O₅ (99.99%), and Bi₂O₃ (99.9%) as starting materials. The ball-milled powders according to the target stoichiometry were sintered at 800 °C for 4 h. The calcined products were ball milled again for 4 h and then pressed into pellets uniaxially. The pellets were fired at 1240 °C for 2 h and covered with some calcined powder to reduce Ba and Bi loss during the firing process. The pellet density was estimated using the Archimedes method. The raw materials BaCO₃, Nb₂O₅, Bi₂O₃, TiO₂ (99.5%), and SrCO₃ (99.5%) were used for the preparation of BBNT and SBN using the same method as mentioned above. High-angular resolution synchrotron X-ray powder diffraction (SPD) data were collected using a Debye–Scherrer camera with an imaging plate on beam line BL02B2 at SPring-8, Japan (RT; wavelength = 0.9980 Å). The structure was refined by the Rietveld method using Jana2006 software.

AC impedance spectroscopy measurements from 200 °C to 600 °C in air were carried out with a Solartron SI 1260 impedance analyzer over the frequency range from 0.1 Hz to 1 MHz with an AC measuring voltage of 100 mV. Dielectric parameters were measured as a function of temperature at a fixed frequency using an impedance analyzer (Agilent 4294A). Before the measurements, silver paste was coated onto both sides of the polished pellet, to be used as an electrode and fired at 650 °C for 30 min to burn the organic components. The complex impedance data were corrected for the sample geometry (thickness/area of pellet) and analyzed using the ZView software (version 3.4b Scribner Associates Inc., USA). The AC impedance spectra were also obtained on the BBNT and SBN pellets for comparison. Impedance measurements of BBN were also performed under air and Ar gas flows to examine whether the impedance data changed with the oxygen partial pressure, which would provide some information about the possible oxide ion conduction in BBN ceramics.

3. Results and discussion

3.1 Crystal structure

The high-angular resolution of the SPD profile makes it possible to determine the crystal structure of BBN accurately. A preliminary LeBail fitting carried out on the SPD data showed that BBN was a tetragonal phase with a = 12.533(6) Å and c = 3.923(2) Å. On the basis of the systematic absences of the space group, P4bm (no. 100) and P4/mbm (no. 127) were assigned. However, the non-centrosymmetric space group P4bm was excluded since the second harmonic generation (SHG) signal was not detected in the BBN sample. The starting P4/mbm model reported previously in the paraelectric phase of Pb₂K_0.5Li_0.5Nb₅O₁₅ (ref. 3) was used for refinements of the SPD pattern, and the barium, niobium and oxygen contents were fixed to the nominal stoichiometry. Crystallographic data of BBN refined from the SPD pattern are listed in Table 1. The experimental, calculated, and difference profiles are shown in Fig. 1, while the refined structural parameters and crystal structure are shown in Table 2 and Fig. 2. The possible distributions of Ba²⁺ and Bi³⁺ in different A sites were tested in the refinement process. The big Ba atoms are prone to occupy A2 sites due to the negative convergence in the A1 sites. Then, the smaller Bi atoms reside in the rest of the A sites. Compared to the Ba atom, the smaller Bi atom seems to have an irregular distribution in A1 and A2 sites. The A1 sites are only occupied by 52.09% Bi, while the A2 sites are occupied by 24.95% Bi and 50.0% Ba, implying that about 1/3 of the A sites are vacant, which is uncommon in the TTB structures. The refinements for the room temperature (RT) data showed that the isotropic displacement factor U_iso for Bi atoms at the A2 sites was abnormally large, while the refinement of the atomic anisotropic displacement factors (ADPs) for the Bi atoms at the A2 sites improved the fitting remarkably. The prolate shapes of the thermal ellipsoids in Fig. 2(a), which are extremely large, suggest the split of Bi at the A2 sites. Finally, a multiple-split of Bi atoms in the A2 sites evolved, which is depicted as the butterfly-like atomic clusters in Fig. 2(b). This split may be in correlation with the asymmetric electronic-shell environments of the Bi cations with 6s² lone pairs. In the literature,^24,25 the substitution of Bi³⁺ (1.16 Å, CN = 8) in BBN by La³⁺ (1.17 Å, CN = 8) (i.e. BaLaNb₅O₁₅) leads to lanthanum niobate impurities, indicating that the split of Bi atoms in pentagonal cavities is in favor of the stability of tetragonal tungsten bronze, particularly with large numbers of cationic vacancies. The final refined chemical formula is Ba₂Bi_2.04Nb₁₀O₃₀, and the EDS gives the cations ratio of Ba₂Bi_1.89Nb_9.24 (error < 5%, shown in Table S1 in ESI†), suggesting that the sample is stoichiometric. Moreover, the EDS mapping displays uniform elements distributions (Fig. S2†). The phase also shows it is structurally stable at 800 °C in reducing conditions (Fig. S3 and S4†).

Table 1 Crystallographic data of BBN refined from SPD at room temperature

	RT (SPD)
Rp	3.37%
Rwp	5.43%
χ^2	3.15
Space group	P4/mbm
a (Å)	12.5337(1)
c (Å)	3.9232(1)
15-coordinated site (A2)	24.95% Bi, 50.0% Ba, 25.05% vacancy
12-coordinated site (A1)	52.09% Bi, 48.91% vacancy

---

Fig. 1 Rietveld fit pattern for the high-resolution synchrotron X-ray powder diffraction (SPD) data of BBN collected at RT with the space group P4/mbm.

Table 2 The final refined structural parameters of BBN at RT with the split of Bi in the A2 sites

Atom	Site	x	y	z	Uiso (Å^2)	Occupancy
Ba2	4h	0.6736(3)	0.1736(3)	0.5	0.0152(7)	0.5
Bi2	8j	0.6169(17)	0.2457(27)	0.5	0.0077(97)	0.0251(3)
Bi2a	8j	0.5936(10)	0.1816(11)	0.5	0.0301(39)	0.0747(3)
Bi2b	4h	0.7867(18)	0.7133(17)	0.5	0.0290(8)	0.0499(3)
Bi1	2b	0	0	0.5	0.0847(13)	0.5209(3)
Nb1	2d	0	0.5	0	0.0109(6)	1
Nb2	8i	0.2114(1)	0.0740(1)	0	0.0116(4)	1
O1	2c	0	0.5	0.5	0.0304(16)	1
O2	4g	0.2146(5)	0.7146(5)	0	0.0154(12)	1
O3	8i	0.0685(6)	0.1425(5)	0	0.0154(12)	1
O4	8i	0.0058(5)	0.3428(6)	0	0.0154(12)	1
O5	8j	0.7867(18)	0.7133(18)	0.5	0.0304(16)	1

---

Fig. 2 (a) Schematic structure of BBN at RT refined with the anisotropic displacement parameters. The large size of the ellipsoids in the A2 site indicates the split of Bi atoms. (b) Final structure of BBN at RT with multiple-splits of Bi in the A2 sites.

3.2 Electrical conductivity characterization

The electrical conductivities of the BBN, SBN and BBNT ceramics were measured by impedance spectroscopy using pellets fired at 1240 °C for 2 h. AC impedance spectroscopy normally resolved the grain (bulk), grain boundary, and electrode response according to their characteristic relaxation time, showing successive semicircles in a complex plane. Impedance data in the form of a complex plane plot for BBN, SBN and BBNT measured at 600 °C in air are shown in Fig. 3. The BBN sample exhibited a single semicircle arc and a spike within the measured frequency range. The extracted ε_r is ∼350, obtained from the single arc using the relation ωRC = 1 at the arc maximum and the formula C = ε_rε₀A/d (where ω is the angular frequency corresponding to the maximum Z′′, A is the electrode area, d is the sample thickness, and ε₀ is the permittivity of free space). This is consistent with the permittivity value of ∼360 obtained from the temperature dependence of the relative permittivity at the fixed frequency (1 MHz), as depicted in Fig. 7, indicating that the arc is associated with a bulk response.^26,27 The spike corresponding to the Warburg electrode response was observed in the low frequency range 1–0.1 Hz, which shows a capacitance of ∼10⁻⁶ to 10⁻⁵ F cm⁻¹ and is assigned as the ionic conduction response.²⁸ The spikes for SBN and BBNT, however, are not distinct with relatively larger resistivities of 225 kΩ cm⁻¹ and 550 kΩ cm⁻¹ (the resistivities were estimated from the intercept of the semicircle arc at low frequency). We may speculate that the electrical conductivity in BBN is dominated by ionic conduction, as compared with SBN and BBNT.

Fig. 3 Complex impedance plots for the BBN measured in air at 600 °C (a), SBN at 600 °C (b) and BBNT at 600 °C (c). The low frequency tail or spike is ascribed to the electrode response.

It is notable that no significant grain boundary contribution was observed in the impedance data for BBN at 600 °C, similar to that at lower temperatures (see Fig. S8†). The impedance data were replotted as the imaginary parts of the complex impedance Z′′ and electric modulus, M′′, against frequency on a double-logarithmic scale, Fig. 4. The maxima of the M′′ spectra are dominated by components with the smallest capacitance, while the maxima in the Z′′ spectra are sensitive to components with the largest resistance. The Z′′/M′′ curves show only a single Debye-type peak in both cases with the maxima at similar frequencies, indicating that the sample may be electrically homogeneous and could be represented by a single parallel RC element.²⁸ In addition, the overlap of the Z′′ and M′′ peaks in the spectra reflects the domination of the long-range migration of ions at 600 °C.²⁹ The capacitance, C′, as a function of frequency (see Fig. 4 inset section) showed a frequency-independent plateau in the high frequency region, which corresponds to the bulk response with relative permittivity values of ∼360.

Fig. 4 Z′′/M′′ spectroscopic plots. The inset is the C′ spectroscopy plot at 600 °C for BBN sintered for 2 hours.

The Arrhenius plots of TTB-type BBN, SBN, and BBNT are shown in Fig. 5. The conductivity data of BBN sintered at 1240 °C for 10 h were also plotted for comparison. The total conductivity of BBN sintered at 1240 °C for 10 h varied within 10⁻⁵ to 3 × 10⁻⁴ S cm⁻¹ with an activation energy of 0.3–0.42 eV over the 250–600 °C range. The SBN and BBNT ceramics showed lower conductivities and larger activation energies. The relative low activation energy for BBN is unusual in TTB compounds, and this will be discussed in Section 3.4 below.

Fig. 5 Comparison of total electrical conductivity of the three TTB-structure BBN, SBN, BBNT pellets measured in air, which were sintered at 1240 °C for 2 hours. Conductivity data of BBN sintered at 1240 °C for 10 hours were also plotted for comparison.

Impedance spectroscopy measurement was employed under different gas atmospheres (see Fig. S5†). There was no distinct change in bulk electrical conductivity at 550 °C by varying the p_O2 from air to Ar gas. When measured in 10% H₂/90% N₂, however, the ceramic showed a much lower resistance, indicative of some n-type electronic conductivity at more reducing atmospheres. It could be concluded that the migration ions are oxygen ions. The ionic transport number was evaluated to be 0.66–0.94 at 250–600 °C in air (see Fig. S9†). Actually, the SBN ceramic should show a larger ionic conductivity due to the smaller Sr²⁺ ions if the migration ions are Ba²⁺ ions in BBN ceramic.

3.3 Dielectric properties

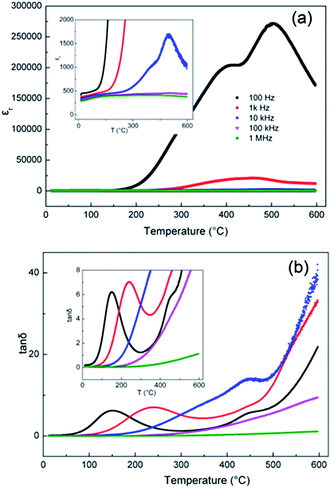
The temperature dependence of the permittivity ε_r and dielectric loss tan δ for BBN at fixed frequencies of 0.1, 1, 10, 100 kHz and 1 MHz over the temperature range from RT to 600 °C are shown in Fig. 6. Two giant permittivity peaks of ∼2 × 10⁵ and 2.8 × 10⁵ at 100 Hz at 400 °C and 600 °C, respectively, can be observed, while at higher frequencies (>10 kHz), no peaks are observed. This phenomenon is in accordance with the capacitance data as a function of frequency in Fig. 4 (inset section), which shows a sharp increase as the frequency decreases. The giant permittivity peaks are not associated with the intrinsic bulk response, but rather with the Warburg electrode response that arises from the formation of electric double layers at the electrode–sample interface. This also confirms the ionic conduction in BBN. Loss tan δ peaks at low frequencies (<10 kHz) below 500 °C are observed. The dielectric relaxation peaks may be associated with the short-range hopping of oxygen vacancies, since oxygen vacancies are active at low frequency and act as “polarons”, similar to with the reorientation of the dipole.^30,31

Fig. 6 The temperature dependences of the dielectric permittivity ε_r (a), and loss tan δ (b) at different fixed frequencies from 100 Hz to 1 MHz for BBN pellets sintered for 2 h at 1240 °C. Insets are an expanded view of the data between RT and 600 °C.

The temperature dependencies of the dielectric permittivity ε_r and loss tan δ at 1 MHz for BBN, SBN, BBNT and BBN10 (sintered at 1240 °C for 10 h) pellets between RT and 600 °C are shown in Fig. 7. There are no sharp dielectric peaks in these TTB compounds, Fig. 7(a), due to their paraelectric properties above room temperature since these compounds exhibit typical relaxor behaviors with a broad phase transition T_m, which is lower than the room temperature.³² It can be seen that the dielectric loss of BBN is much larger than SBN and BBNT, indicative of the higher conductivity associated with ion conduction in BBN. In contrast, the dielectric loss markedly increased for BBN with the extension of the sintering time from 2 h to 10 h. The large dielectric loss may arise from the oxygen vacancies generated from the volatilization loss of Bi₂O₃ during the ceramic processing, in terms of the Kroger–Vink equation,^26,27

Fig. 7 Temperature dependence of (a) dielectric permittivity ε_r and (b) loss tan δ at 1 MHz from RT to 600 °C for BBN, BBN 10 h, SBN, and BBNT. The BBN 10 h pellet was sintered at 1240 °C for 10 h, and the others for 2 h with an impedance analyzer Agilent 4294A.

The increase in dielectric loss and total electrical conductivity with the extension of sintering time may derive from the greater loss of Bi₂O₃. Unfortunately, the loss amount is too small to be measured using the common chemical techniques such as ICP and EDS.²⁶ Other migration ion species can be excluded since the bulk conductivity would not increase significantly with the extension of sintering time.

3.4 Conduction mechanism

Why BBN ceramic shows a larger oxide ion conductivity compared with SBN and BBNT is an intriguing issue. It can be noted that the larger cell parameters of BBN compared with SBN (see Fig. S6 in ESI†) can provide more free space for the hopping of oxide ions, since the ionic radius of Ba (1.61 Å, CN = 12) is much larger than that of Sr (1.44 Å, CN = 12).³³ This may be associated with the relative low enthalpies for oxide ion hopping or activation energy as mentioned above. The smaller, stiffer lattices of SBN offer less dynamics and the oxide ions mobility decrease. This is analogous to the situation wherein Gd-doped CeO₂ shows a much larger oxide ion conductivity than Y-doped ZrO₂.¹¹

On the other hand, the cationic vacancies account for about 1/3 of the total A sites for BBN, which is different from perovskite-structured compounds with fully-occupied A sites, which may also increase the oxide ion mobility. When the A sites of a TTB-type compound are fully filled with cations, for example, in BBNT, the conductivities decrease significantly and the activation energy increases obviously (see Fig. 5 and S7 in ESI†). Such cationic vacancies in BBN may be responsible for the lower activation energy of ∼0.3–0.5 eV. Actually, many Bi-based oxide compounds^26,34–37 are oxide ion conductors. The highly polarizable cation Bi³⁺, whose 6s² lone pair electrons are known to be highly stereochemically active and hybridized easily, is suitable for anion migration, and the formation of oxygen defects is favored by the weak Bi–O bond. For BBN, the multiple-split of Bi atoms in A2 sites brings about a variety of Bi–O bond lengths (see Table S2 in ESI†). This may facilitate the migration of oxide ions.

4. Conclusions

The present study reveals that a Bi-based TTB-type oxide, BaBiNb₅O₁₅, exhibits an oxygen ion conductivity of 3 × 10⁻⁴ S cm⁻¹ at 600 °C with a relatively low E_a (0.3–0.5 eV), which shows the best oxide ion conductivity among TTBs. The structure was determined by high-resolution synchrotron X-ray powder radiation, and the compound was seen to crystallize in the tetragonal centric space group P4/mbm with a = 12.5337(1) Å and c = 3.9232(1) Å. The electrical properties were studied by impedance spectroscopy, and the dielectric properties were also discussed. It is suggested that the large amount of cationic vacancies in the A sites, the big free space created by the large Ba²⁺ cations, and the split of Bi atoms (significant polarisability) may be in favor of oxygen ion migration. This study shows that TTB oxides may be a new type of an oxygen ion conductivity material.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (grant no. 91022016, 91422301, and 21231001), the Program for Changjiang Scholars and the Innovative Research Team in University (IRT1207), and the Fundamental Research Funds for the Central Universities, China (Grant No. FRF-SD-13-008A). We thank Liuzhen Bian from the University of Science and Technology Beijing for their help in the complex impedance measurement at different atmospheres.

References

1. P. B. Jamieson, S. C. Abrahams and J. L. Bernstein, J. Chem. Phys., 1968, 48, 5048–5056.
2. K. Lin, H. Wu, F. Wang, Y. Rong, J. Chen, J. Deng, R. Yu, L. Fang, Q. Huang and X. Xing, Dalton Trans., 2014, 43, 7037–7043.
3. K. Lin, Y. Rong, H. Wu, Q. Huang, L. You, Y. Ren, L. Fan, J. Chen and X. Xing, Inorg. Chem., 2014, 53, 9174–9180.
4. P. B. Jamieson, S. C. Abrahams and J. L. Bernstein, J. Chem. Phys., 1969, 50, 4352–4363.
5. J. Gardner and F. D. Morrison, Dalton Trans., 2014, 43, 11687–11695.
6. C. A. Kirk, M. C. Stennett, I. M. Reaney and A. R. West, J. Mater. Chem., 2002, 12, 2609–2611.
7. R. R. Neurgaonkar, J. R. Oliver, W. K. Cory, L. E. Cross and D. Viehland, Ferroelectrics, 1994, 160, 265–276.
8. R. J. Xie and Y. Akimune, J. Mater. Chem., 2002, 12, 3156–3161.
9. J. H. Ko, S. Kojima, S. G. Lushnikov, R. S. Katiyar, J. H. Kim and J. H. Ro, J. Appl. Phys., 2002, 92, 1536–1543.
10. P. Ganguly, S. Devi, A. K. Jha and K. L. Deori, Ferroelectrics, 2009, 381, 111–119.
11. L. Malavasi, C. A. J. Fisher and M. S. Islam, Chem. Soc. Rev., 2010, 39, 4370–4387.
12. P. Vernoux, L. Lizarraga, M. N. Tsampas, F. M. Sapountzi, A. de Lucas-Consuegra, J. L. Valverde, S. Souentie, C. G. Vayenas, D. Tsiplakides, S. Balomenou and E. A. Baranova, Chem. Rev., 2013, 113, 8192–8260.
13. J. Sunarso, S. Baumann, J. M. Serra, W. A. Meulenberg, S. Liu, Y. S. Lin and J. C. D. da Costa, J. Membr. Sci., 2008, 320, 13–41.
14. B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352.
15. T. Ishihara, H. Matsuda and Y. Takita, J. Am. Chem. Soc., 1994, 116, 3801–3803.
16. D. J. L. Brett, A. Atkinson, N. P. Brandon and S. Skinner, Chem. Soc. Rev., 2008, 37, 1568–1578.
17. M. S. Khan, M. S. Islam and D. R. Bates, J. Phys. Chem. B, 1998, 102, 3099–3104.
18. M. S. Islam, J. Mater. Chem., 2000, 10, 1027–1038.
19. J. A. Kilner and R. J. Brook, Solid State Ionics, 1982, 6, 237–252.
20. R. L. Cook and A. F. Sammells, Solid State Ionics, 1991, 45, 311–321.
21. A. Kaiser, J. L. Bradley, P. R. Slater and J. T. S. Irvine, Solid State Ionics, 2000, 135, 519–524.
22. M. Prades, N. Masó, H. Beltrán, E. Cordoncillo and A. R. West, Inorg. Chem., 2013, 52, 1729–1736.
23. X. Kuang, F. Pan, J. Cao, C. Liang, M. R. Suchomel, F. Porcher and M. Allix, Inorg. Chem., 2013, 52, 13244–13252.
24. K. Masuno, J. Phys. Soc. Jpn., 1964, 19, 323–328.
25. J. K. Wang, N. Wakiya, K. Shinozaki and N. Mizutani, Electroceramics in Japan III, 2000, 181–182, 31–34.
26. M. Li, M. J. Pietrowski, R. A. de Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35.
27. M. Li, H. Zhang, S. N. Cook, L. Li, J. A. Kilner, I. M. Reaney and D. C. Sinclair, Chem. Mater., 2015, 27, 629–634.
28. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138.
29. R. Gerhardt, J. Phys. Chem. Solids, 1994, 55, 1491–1506.
30. C. Ang, Z. Yu and L. E. Cross, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 228–236.
31. X. P. Wang, Q. F. Fang, Z. S. Li, G. G. Zhang and Z. G. Yi, Appl. Phys. Lett., 2002, 81, 3434–3436.
32. A. Simon and J. Ravez, Phys. Status Solidi A, 2003, 199, 541–545.
33. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
34. J. C. Boivin and G. Mairesse, Chem. Mater., 1998, 10, 2870–2888.
35. X. Kuang, J. L. Payne, J. D. Farrell, M. R. Johnson and I. R. Evans, Chem. Mater., 2012, 24, 2162–2167.
36. Y. Li, T. P. Hutchinson, X. Kuang, P. R. Slater, M. R. Johnson and I. R. Evans, Chem. Mater., 2009, 21, 4661–4668.
37. S. Sanna, V. Esposito, J. W. Andreasen, J. Hjelm, W. Zhang, T. Kasama, S. B. Simonsen, M. Christensen, S. Linderoth and N. Pryds, Nat. Mater., 2015, 14, 500–504.

---

Footnote

† Electronic supplementary information (ESI) available: Structure model of TTB, SEM micrograph of BBN, complex impedance plots of BBN measured in different atmospheres, XRD patterns of BBN at different temperatures, XRD patterns of BBN, SBN, and BBNT samples, cell parameters of BBN and SBN versus temperature, Rietveld pattern of BBNT, selected bond lengths of BBN. Complex impedance plots at 250 °C and 400 °C and for YSZ-coated samples. See DOI: 10.1039/c5ra10635d

---