Mineral carbonation of a desulfurization residue for CO2 sequestration
Wenjin Dingab,
Huaming Yang*abc and
Jing Ouyang*ab
aCentre for Mineral Materials, School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China. E-mail: hmyang@csu.edu.cn; jingouyang@csu.edu.cn; Fax: +86-731-88710804; Tel: +86-731-88830549
bKey Laboratory for Mineral Materials and Application of Hunan Province, Central South University, Changsha 410083, China
cState Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
First published on 28th July 2015
Abstract
The feasibility of mineral carbonation of a desulfurization residue for sequestering CO2 was evaluated both through theoretical and experimental approaches. The carbonation reaction, including carbonation of Ca(OH)2 and CaSO4, occurred through a kinetically controlled stage with an activation energy of 20.21 kJ mol−1. The concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperature impacted on the carbonation ratio of the desulfurization residue through their direct and definite influence on the rate constant. Concentration of ammonia and liquid to solid ratio were the most important factors influencing the desulfurization residue carbonation in terms of both the carbonation ratio and reaction rate. Under optimized conditions the carbonation ratio could reach approximately 98% when using industry-grade CO2. The crystalline phases of the carbonated desulfurization residue were calcite and vaterite with spherical and granular morphology. CO2/O2/N2 mixed gas was also used as the simulated desulfurization fuel gas in the carbonation reaction and it had a relatively minor effect on the carbonation ratio. However, it slowed the carbonation reaction and produced a carbonation product with a smaller average particle size, which included high purity (≥99%) white calcite. The carbonated desulfurization residue reported herein showed a rapid CO2 sequestration ratio, high CO2 sequestration amount, low cost, and a large potential for in situ CO2 sequestration in the electricity and steel industry.
1. Introduction
Current warming of the global climate is considered to be caused by increasing emissions of anthropogenic greenhouse gases since pre-industrial times, in particular the emissions of CO2.1–3 The control of greenhouse gas emissions is arguably the most challenging environmental policy issue that has been encountered, both in China and elsewhere.4–6 Continued uncontrolled greenhouse gas emissions may lead to rising sea levels and species extinction. In 2013, global CO2 emissions hit a new record, reaching about 36.1 billion tons. Among them, China's emissions of 10 billion tons account for nearly a third of the global CO2 emissions.7 The global carbon cycle is sufficiently extensive to conclude that natural processes cannot absorb all the anthropogenically produced carbon dioxide (CO2) in the coming centuries, so adaptation technologies are urgently required.8,9 Mineral carbonation has recently been considered as a leading method for CO2 sequestration. The technology is based on the reaction of CO2 with an alkaline metal oxide to form stable carbonates, typically of calcium (CaCO3) or magnesium (MgCO3). Many natural minerals containing large quantities of primary cations (Ca2+ and Mg2+), such as olivine, serpentine and wollastonite, have been evaluated for CO2 sequestration.9–17 The carbonation of natural minerals often requires harsh reaction conditions because the natural minerals are thermodynamically stable. Furthermore, the added costs of mining, grinding, and separation of natural minerals from the source rock, which is in some sense also a waste of resources, make natural mineral carbonation less applicable to industrial development.18Solid wastes may also contain many alkaline metal ions, and their use for CO2 sequestration has several advantages over using natural minerals. The advantages offered by solid wastes include: (1) they supply a readily available source of calcium or magnesium mineral matter without any need for pre-processing; (2) they are typically fine-grained with high reactive surface areas; (3) the environmental quality of the waste materials accumulation area can be improved through pH-neutralization and mineral transformation; and (4) the carbonation product may be amenable for beneficial reuse as road base or other construction materials.19,20 Researchers have studied carbonation with a range of wastes including steel slag,21–24 mining residues,25 coal ash,26 and waste concrete and blast furnace slag.27,28 Desulfurization residue is a kind of solid wastes, and it is mostly generated during the process of removing SOx from flue gas streams from power generation and sintering plants. The residue generally contains rich calcium. And desulfurization residue is produced in the form of a fine powder, it can be used directly in the carbonation process without pre-processing. Approximately 20 Mt of desulfurization residue is produced in China each year with only 15% of this being recycled,29 suggesting that approximately 5–7 Mt of CO2 could be sequestered annually if all available desulfurization residue were used for mineral carbonation.
To our knowledge, there have few reports about the flue gas desulfurization gypsum carbonation for CO2 sequestration,30–32 but they all focused on the effects of process conditions on the results, and the composition of desulfurization gypsum is much simpler than that of desulfurization residue.
In this paper, desulfurization residue was used in the carbonation experiments, and ammonia was employed as the reaction media to speed up the reaction. The feasibility of this route was investigated by using both theoretical and experimental approaches. The underlying mechanism was further discussed by kinetic analysis during the carbonation reaction.
2. Experimental
2.1 Materials preparation
The desulfurization residue, with clubbed and granular morphology (Fig. 1a and b), used in this study was obtained from China Wuhan Iron and Steel Corp. The main phase of the desulfurization residue sample was gypsum that also contained some calcium hydroxide (Fig. 1c). The major constituents were CaO, SO3 and combined water, and the major impurities were SiO2, Fe2O3 and Al2O3. The detailed composition is presented in Table 1. The particle size was measured using a particle size analyzer (LS-POP(6), Zhuhai OMEC Instrument Co., Ltd, China). The average (d50) particle size was 35.92 μm and over 90% of the particles were smaller than 80 μm (Fig. 1d). Gaseous CO2 was first supplied from bottled sources at industry-grade of 99.9% purity. In later tests CO2 was supplied as a part of a mixture that simulated desulfurized flue gas. After removal of SOx, desulfurized flue gas typically contains 5–10% CO2, 10–15% O2, 75–80% N2. To evaluate the feasibility of the carbonation experiment with a CO2/O2/N2 gas mixture similar to that from a steel or iron plant a mixture of 75% N2, 15% O2 and 10% CO2 was used.| CaO | SO3 | SiO2 | Fe2O3 | Al2O3 | H2O | Others |
|---|---|---|---|---|---|---|
| a The chemical elements in the desulfurization residue are in the form of oxides. | ||||||
| 48.45 | 25.75 | 0.55 | 1.98 | 2.49 | 18.1 | 2.68 |
For each experiment 20 g of desulfurization residue was placed into a 400 mL reaction vessel with a predetermined volume and concentration of ammonia solution then added. A magnetic stirrer was used to ensure adequate mixing while a hot-water bath maintained the desired reaction temperature. The CO2-rich gas was injected with a predetermined flow rate at normal pressure. A pH meter was installed to monitor the progress of the carbonation reaction. The pH value was recorded at 2 min intervals until the pH value was relatively constant. The mixture was then filtered to separate the solids from the solution before the solids were washed with distilled water and dried in an oven at 110 °C for approximately 24 h. Detailed experimental conditions for each set of experiments are listed in Table 2.
| Desulfurization residue (g) | Ammonia concentration (mol L−1) | CO2 flow rate (mL min−1) | Liquid to solid ratio (mL g−1) | Temperature (°C) | CO2 purity (%) | |
|---|---|---|---|---|---|---|
| A1 | 20 | 1 | 200 | 5 | 30 | 99.9 |
| A2 | 20 | 2 | 200 | 5 | 30 | 99.9 |
| A3 | 20 | 3 | 200 | 5 | 30 | 99.9 |
| A4 | 20 | 4 | 200 | 5 | 30 | 99.9 |
| B1 | 20 | 3 | 50 | 5 | 30 | 99.9 |
| B2 | 20 | 3 | 100 | 5 | 30 | 99.9 |
| C1 | 20 | 3 | 100 | 3 | 30 | 99.9 |
| C2 | 20 | 3 | 100 | 8 | 30 | 99.9 |
| D1 | 20 | 3 | 100 | 5 | 20 | 99.9 |
| D2 | 20 | 3 | 100 | 5 | 40 | 99.9 |
| E1 | 20 | 3 | 300 | 5 | 30 | 10 |
| E2 | 20 | 3 | 400 | 5 | 30 | 10 |
| E3 | 20 | 3 | 500 | 5 | 30 | 10 |
2.2 Characterization
The composition of the sample was determined by X-ray fluorescence (XRF) and chemical titration. Powder XRD measurements of the samples were conducted with a DX-2700 X-ray diffractometer using Cu Kα radiation (λ = 0.15406 nm) at a scanning ratio of 0.02 degree per s with a voltage of 40 kV at 40 mA. SEM was performed by a JEOL JSM-6360LV scanning electron microanalyzer with an accelerating voltage of 5 kV. The carbonation ratio (η) and the CO2 sequestration efficiency (ε) were calculated according to the following equation:
 | (1) |
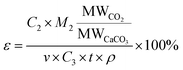 | (2) |
3. Results and discussion
In the gas–liquid–solid system, the overall possible chemical reactions are expressed by eqn (3)–(6). To illustrate the theoretical feasibility of the route proposed above, the thermodynamic parameters at the standard state in the carbonation processes of desulfurization residue were calculated.| Ca(OH)2(aq) + CO2(aq) → CaCO3(s) + H2O(1) ΔG (kJ mol−1) = −75, K = 1.40 × 1013 | (3) |
| 2NH4OH(aq) + CO2(aq) → (NH4)2CO3(aq) + H2O(l) ΔG (kJ mol−1) = −276, K = 2.40 × 1048 | (4) |
| CaSO4(s) + (NH4)2CO3(aq) → CaCO3(s) + (NH4)2SO4(aq) ΔG (kJ mol−1) = −22, K = 7.18 × 103 | (5) |
| Ca(OH)2(aq) + (NH4)2CO3(aq) → CaCO3(s) + 2NH4OH(aq) ΔG (kJ mol−1) = +201, K = −1.71 × 1035 | (6) |
From the thermodynamic calculation results, the Gibbs free energy changes (ΔG) are −75, −276 and −22 kJ mol−1 for eqn (3)–(5). They are all less than zero. And their corresponding equilibrium constants (K) are 1.40 × 1013, 2.40 × 1048 and 7.18 × 103. They are all greater than zero. So, eqn (3)–(5) can proceed spontaneously, and they can be regarded as the irreversible exothermic reaction. The Gibbs free energy change (ΔG) is +201 kJ mol−1 > 0 for eqn (6). And the corresponding equilibrium constant (K) is −1.71 × 1035 < 0. So, eqn (6) can not proceed spontaneously in the carbonation process. Through the above analysis, the proposed route is theoretically feasible. And the desulfurization residue carbonation can be summarized into the following two steps: carbonation of Ca(OH)2 and carbonation of CaSO4.
The influence of concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperature on the carbonation of desulfurization residue were shown in Fig. 2–5, respectively. Fig. 2a showed the change of the pH of the reaction solution with time. The initial pH value was approximately 12.5 but decreased over time as the ammonia reacted to form ammonium carbonate, while the carbonation ratio gradually increased (Fig. 2b). Values of pH eventually stabilized at approximately 7, which signified the end of the reaction. Except for A1 (1 mol L−1) and A2 (2 mol L−1), the carbonation ratios were over 90% when the carbonation reactions were finished. In the cases of both A1 and A2, however, the carbonation reaction was not completed due to a lack of ammonia. Because the carbonation ratio did not increase after 60 min, then it should correspond to the virtual termination of the reaction, which was confirmed from pH value of 7. Thus, it could be determined that the termination time of carbonation was simply by monitoring the pH variation time as shown in Fig. 2a. For the high ammonia experiment, A4 (4 mol L−1), the high terminal pH value of 7.6 indicated that there was excess ammonia, thus 3 mol L−1 was chosen as the optimum ammonia concentration.
 | ||
| Fig. 2 Effect of ammonia concentration on the desulfurization residue carbonation sample (a) pH of solution, (b) carbonation ratio of product. | ||
 | ||
| Fig. 3 Effect of CO2 flow rate on the desulfurization residue carbonation sample (a) pH of solution, (b) carbonation ratio of product, and (c) CO2 sequestration efficiency of product. | ||
 | ||
| Fig. 4 Effects of liquid-to-solid ratio on the desulfurization residue carbonation sample: (a) pH value of solution, (b) carbonation ratio of product. | ||
 | ||
| Fig. 5 Effects of reaction temperature on the desulfurization residue carbonation sample (a) pH value of solution, (b) carbonation ratio of product. | ||
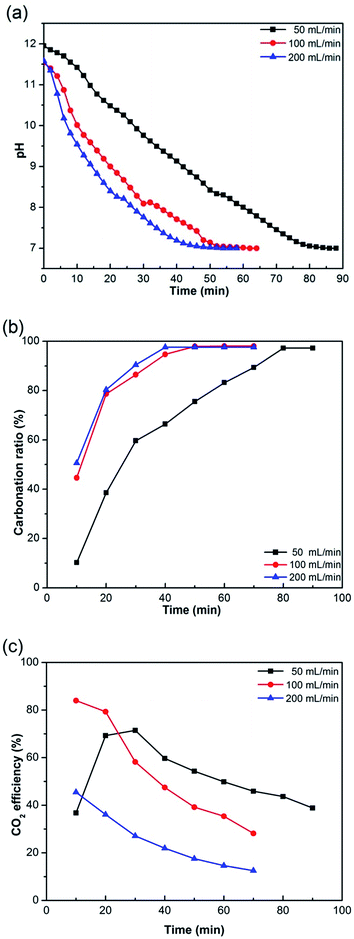
The effect of the CO2 flow rate on the desulfurization residue carbonation was evaluated by considering CO2 flow rates of 50, 100 and 200 mL min−1 (B1, B2 and A3, respectively). At 200 mL min−1, the pH of the solution reached 7, indicating that the reaction had completed, after 50 min (Fig. 3a). When the flow rate was decreased to 100 and 50 mL min−1, the time required for the pH to reach 7 increased to 55 and 80 min, respectively. This suggested that an increase in the CO2 flow rate accelerated the carbonation reaction. In addition, Fig. 3b showed that over 90% of the gypsum and calcium hydroxide were converted to calcium carbonate in approximately 50 min when the CO2 flow rate was 200 mL min−1. However, a comparable conversion was only achieved after 80 min when the flow rate was 50 mL min−1. Despite this, it was not always advantageous to increase CO2 flow rate to obtain a higher reaction rate. Because the CO2 flow rate should be considered both by the reaction time and the CO2 sequestration efficiency. Fig. 3c showed the effect of CO2 flow rate on the CO2 sequestration efficiency of product. As the reaction progress, the CO2 sequestration efficiency was decreased. The CO2 sequestration efficiency was 38.83% after 10 min when the flow rate was 50 mL min−1, while it can reach approximately 84% when the flow rate was 100 mL min−1 (Fig. 3c). And it needed less time to finish the reaction when the CO2 flow rate was 100 mL min−1 compared to 50 mL min−1. When the CO2 flow rate was 200 mL min−1, it needed the same time to finish the reaction compared to 100 mL min−1, but it had lower CO2 sequestration efficiency (Fig. 3c).
The effect of the liquid to solid ratio on the carbonation of desulfurization residue was evaluated by adjusting the ratio from the range of 3–8 mL g−1 (C1, B2 and C2). A period of approximately 60 min was required to complete each reaction and the pH value of the solution was not significantly affected by changing the liquid to solid ratio (Fig. 4a). However, Fig. 4b showed that the liquid to solid ratio affected the carbonation ratio, which fell from 98% for B2 and C2 to 90% when the liquid to solid ratio was 3 mL g−1. This indicated that the carbonation reaction was incomplete because of the lack of ammonia. The conditions in B2 were chosen as the optimal liquid to solid ratio.
The effect of the reaction temperature on the carbonation of desulfurization residue was evaluated by considering the temperatures of 20, 30 and 40 °C (D1, B2 and D2). The influence of reaction temperature on the desulfurization residue carbonation was not as strong as that of concentration of ammonia and CO2 flow rate. Fig. 5a showed the pH variation of the reaction solution over time and showed that reaction time decreased with an increase in the reaction temperature. For all three experiments carbonation ratios of over 95% were observed (Fig. 5b). Considering the tradeoff between reaction time and energy consumption for heating, 30 °C (B2) was chosen as the optimal reaction temperature.
The above research has clearly demonstrated the feasibility of using desulfurization residue for CO2 sequestration with industry-grade. By following the optimized process, the carbonation ratio (η) can reach 98%, and 1 t desulfurization residue was able to sequester 373 kg of CO2, a value greater than the other solid wastes obtained previously (Table 3). And approximately 1 t of desulfurization residue can absorb 373 kg of CO2, where the process required 3.9 t of water and 1 t of industrial ammonia. In the carbonation process, ammonia can be recycled by calcining intermediate ((NH4)2SO4). And 1 t ammonium sulphate was able to prepare 177 kg of ammonia. 1 t desulfurization residue was able to produce 900 kg of ammonium sulphate, and it can recycle 160 kg of ammonia ($12). Combining with previous research,33 we preliminarily estimated that the total cost of the whole desulfurization residue carbonation process (including energy consumption, reagent recovery and the value of the recycled agent) may be around $92 (Table 4), much lower than that of previous methods.33,34
| Raw material | Process conditions | Results | References |
|---|---|---|---|
| Coal fly ash | 75 °C, 50 g L−1, 0.3 MPa, 600 rpm, 4.5 h | 230 kg(CO2) t−1 | 39 |
| Steel slag | Pretreated from 200 °C to 900 °C, carbonation at 600 °C for 5 min at atmospheric pressure | 113 kg(CO2) t−1 | 40 |
| Blast furnace slag | Acetic acid and sodium hydroxide were used as agents, carbonation at atmospheric pressure and 30 °C | 227 kg(CO2) t−1 | 28 |
| Desulfurization gypsum | NH4OH was used as agent, carbonation at room temperature and atmospheric pressure | 243 kg(CO2) t−1 | 30 |
| Mining residues | Carbonation at room temperature and atmospheric pressure | 1.2–3.7 kg(CO2) t−1 | 41 |
| Oil shale ash | Carbonation at room temperature and atmospheric pressure | 90 kg(CO2) t−1 | 42 |
| Desulfurization residue | NH4OH was used as agent, carbonation at room temperature and atmospheric pressure | 373 kg(CO2) t−1 | This work |
| Feed material | Costs ($ t−1) | Treatment methodology | Treatment energy consumption kWh t−1 | Total costs ($) |
|---|---|---|---|---|
| Desulfurization residue | 20 | Grinding | — | 92 |
| Water | 0.735 | Stiring (400 rpm) | 8 | |
| NH4OH | 75 | Heat treatment | — | |
| Filtering | 3 | |||
| Ammonium sulphate | Calcination | 50 |
The reaction products from the desulfurization residue carbonation experiments were examined using XRD and SEM. After the carbonation reaction, the product containing calcium carbonate with purity above 94% and the crystalline phase of the carbonated desulfurization residue was mainly calcite with some vaterite also present (Fig. 6a), indicating the successful carbonation of desulfurization residue at a low temperature and ambient pressure under the action of ammonia. Fig. 6b showed the morphology and microstructure of carbonation products in the desulfurization residue after reaction with industry-grade CO2. The carbonated sample showed a large number of spherical and granular particles, and they were agglomeration together (Fig. 6b).
Desulfurization residue is mostly generated from power generation and sintering plants. The generation of desulfurization residue is accompanied by a large amount of carbon dioxide emissions, so we explored the experiments that the desulfurization residue carbonation for CO2 sequestration with the simulated desulfurized flue gas in the following study. The experimental conditions used for simulated desulfurized flue gas were exactly the same to those used for the industry-grade CO2 gas (except for the injection rate), and they were listed in Table 2. The injection rates of the gas mixture were 300, 400 and 500 mL min−1 (E1, E2 and E3).
Carbonation conducted by using simulated desulfurized flue gas was found to be slower compared to that conducted by using industry-grade CO2. This fact could be inferred from the lower decrease rate of the pH of the gas mixture (Fig. 7a) compared to that in the case of industry-grade CO2 gas. This tendency was more easily observed in the carbonation ratio curve in Fig. 7b. It could be seen that the carbonation reaction in the case of the gas mixture was not significantly affected through changing the mixed gas flow rate by comparing E1, E2 and E3 (Fig. 7b). The carbonation ratio could reach 90% after the reaction was done for 150 min in the case of E1, E2 and E3. Fig. 8 showed the XRD and SEM results of the carbonation product with simulated desulfurized flue gas. The crystalline phase of the carbonation product was mainly calcite, there was also some vaterite (Fig. 8a), indicating the successful carbonation of desulfurization residue with simulated desulfurized flue gas. The morphology of the carbonation product was rectangular and spherical (Fig. 8c and d). The injection of simulated desulfurized flue gas did not change the crystal phase and morphology of the carbonation product (Fig. 6 and 8), but the particles became smaller. Some calcite with a purity exceeding 99% and good crystal morphology could be obtained in the reaction filtrate in the case that simulated desulfurized flue gas was injected (Fig. 8b and d). Therefore, desulfurized flue gas could be used directly in the desulfurized residue carbonation process without any need for a separate CO2 capture process.
 | ||
| Fig. 7 Effects of CO2–N2–O2 mixed gas on the desulfurization residue carbonation sample (a) pH value of solution, (b) carbonation ratio of product. | ||
The aqueous carbonation of materials with low porosity, such as desulfurized residue, is an irreversible and heterogeneous gas–liquid–solid reaction. CO2 dissolved in the water and reacted with Ca(OH)2 in the desulfurized residue particles and NH4OH. This activity occurs during the kinetically controlled stage or the diffusion-controlled stage. An analysis of the relationship between η and t was conducted to study the kinetics of the desulfurized residue carbonation, in which the reaction kinetic equation of spherical particles (eqn (7)) and the Ginstling equation of spherical particles (eqn (8))35 were adapted to describe the kinetically controlled stage and the diffusion-controlled stage, respectively.
| (1 − η)−2/3 − 1 = k1t | (7) |
| 1 − 2η/3 − (1 − η)2/3 = k2t | (8) |
The relationships of ln[(1 − η)−2/3 − 1] versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t and ln[1 − 2η/3 − (1 − η)2/3] versus ln
t and ln[1 − 2η/3 − (1 − η)2/3] versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t at different concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperatures were shown in Fig. 9 and 10. ln[(1 − η)−2/3 − 1] and ln
t at different concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperatures were shown in Fig. 9 and 10. ln[(1 − η)−2/3 − 1] and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t in Fig. 9 showed a definite linear dependence generally during the carbonation process. While, ln[1 − 2η/3 − (1 − η)2/3] and ln
t in Fig. 9 showed a definite linear dependence generally during the carbonation process. While, ln[1 − 2η/3 − (1 − η)2/3] and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t in Fig. 10 did not well conform to the linear relationship. So, the reaction kinetic equation was a successful fit for the kinetically controlled stage during the carbonation of desulfurized residue regardless of the change in concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperature. However, the irregular and uneven shape of the actual desulfurized residue particles caused the slopes of these curves to deviate from the theoretical value (1.0) in varying degrees.36 The rate constant k1 could be derived and was showed in Table 5. Most of the k1 rate constants derived in this study were higher than those calculated by Sun et al.,37 demonstrating theoretically that the reaction rate of desulfurized residue carbonation was significantly faster than the carbonation showed by Sun et al.37 Concentration of ammonia and liquid to solid ratio were the most important process variables for the desulfurized residue carbonation and had a strong influence on the kinetically stage. k1 increased more than 6 and 4 times, from 0.0335 min−1 at 1 mol L−1 to 0.212 min−1 at 4 mol L−1, and from 0.0528 min−1 at 3 mL g−1 to 0.224 min−1 at 8 mL g−1, respectively. The influence of either the CO2 flow rate or temperature on the carbonation of desulfurized residue was not as notable as the influence of concentration of ammonia and liquid to solid ratio. The final carbonation ratio almost increased when the rate constant k1 increased, indicating that process variables such as concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperature could influence the carbonation ratio of desulfurized residue through a direct and definite influence on the corresponding rate constant.
t in Fig. 10 did not well conform to the linear relationship. So, the reaction kinetic equation was a successful fit for the kinetically controlled stage during the carbonation of desulfurized residue regardless of the change in concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperature. However, the irregular and uneven shape of the actual desulfurized residue particles caused the slopes of these curves to deviate from the theoretical value (1.0) in varying degrees.36 The rate constant k1 could be derived and was showed in Table 5. Most of the k1 rate constants derived in this study were higher than those calculated by Sun et al.,37 demonstrating theoretically that the reaction rate of desulfurized residue carbonation was significantly faster than the carbonation showed by Sun et al.37 Concentration of ammonia and liquid to solid ratio were the most important process variables for the desulfurized residue carbonation and had a strong influence on the kinetically stage. k1 increased more than 6 and 4 times, from 0.0335 min−1 at 1 mol L−1 to 0.212 min−1 at 4 mol L−1, and from 0.0528 min−1 at 3 mL g−1 to 0.224 min−1 at 8 mL g−1, respectively. The influence of either the CO2 flow rate or temperature on the carbonation of desulfurized residue was not as notable as the influence of concentration of ammonia and liquid to solid ratio. The final carbonation ratio almost increased when the rate constant k1 increased, indicating that process variables such as concentration of ammonia, CO2 flow rate, liquid to solid ratio and temperature could influence the carbonation ratio of desulfurized residue through a direct and definite influence on the corresponding rate constant.
| Process variables | k1/10−2 min−1 | R2 | Final η/% | |
|---|---|---|---|---|
| Ammonia concentration (mol L−1) | 1 | 3.35 | 0.944 | 75.5 |
| 2 | 6.85 | 0.95 | 90.28 | |
| 3 | 21.1 | 0.959 | 97.62 | |
| 4 | 21.2 | 0.988 | 98.01 | |
| CO2 flow rate (mL min−1) | 50 | 12.5 | 0.961 | 97.21 |
| 100 | 24.2 | 0.976 | 98.01 | |
| 200 | 21.1 | 0.959 | 97.62 | |
| Liquid to solid ratio (mL g−1) | 3 | 5.28 | 0.958 | 90.58 |
| 5 | 24.2 | 0.976 | 98.01 | |
| 8 | 22.4 | 0.978 | 98.21 | |
| Temperature (°C) | 20 | 16.5 | 0.981 | 97.94 |
| 30 | 24.2 | 0.976 | 98.01 | |
| 40 | 27.8 | 0.983 | 97.81 |
The activation energy, which was E = 20.21 kJ mol−1 (R2 = 0.94) for the kinetically controlled stage was determined through a linear fitting of the plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus 1/T according to the Arrhenius empirical formula.38 The activation energy determined in this study was slightly lower than those reported by Tian et al.,36 which was 21.29 kJ mol−1 and slightly higher than those reported by Sun et al.,37 which was 14.84 kJ mol−1 for the kinetically controlled stage.
k versus 1/T according to the Arrhenius empirical formula.38 The activation energy determined in this study was slightly lower than those reported by Tian et al.,36 which was 21.29 kJ mol−1 and slightly higher than those reported by Sun et al.,37 which was 14.84 kJ mol−1 for the kinetically controlled stage.
4. Conclusions
The carbonation of desulfurization residue was studied both by theoretical and experimental approaches to evaluate the feasibility of its use for CO2 sequestration. The desulfurization residue carbonation reaction followed the kinetically controlled stage mechanism, which could be effectively modeled with the reaction kinetic equation. The activation energy was 20.21 kJ mol−1 for the kinetically controlled stage.Ammonia concentration, CO2 flow rate, liquid to solid ratio and temperature affected the carbonation ratio of desulfurization residue through their direct and definite influence on the rate constant. Ammonia concentration and liquid to solid ratio were the most important process variables influencing the desulfurization residue carbonation in terms of both the carbonation ratio and reaction rate. The influence of either CO2 flow rate or temperature was not as notable as ammonia concentration and liquid to solid ratio.
The desulfurization residue displayed high carbonation reactivity, even at low temperature and atmospheric pressure, producing calcite and vaterite with spherical and granular morphology. Under the optimized conditions (3 mol L−1 ammonia solution, 100 mL min−1 CO2 flow rate, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mL g−1 liquid to solid ratio and a reaction temperature of 30 °C), calcium carbonate with >94% purity could be produced within 60 min with a carbonation ratio of approximately 98% and a maximum CO2 sequestration of 373 kgCO2 tresidue−1. The simulated desulfurization fuel gas in the carbonation reaction had a relatively minor effect on the carbonation ratio. However, it slowed the carbonation reaction and produced a carbonation product with a smaller average particle size, which included high purity (≥99%) white calcite. This technique has the advantage of a rapid CO2 sequestration ratio, low costs, and a large potential for in situ CO2 sequestration in the electricity and steel industry. Therefore, more pilot experiments should be undertaken to provide a practical foundation for future applications.
1 mL g−1 liquid to solid ratio and a reaction temperature of 30 °C), calcium carbonate with >94% purity could be produced within 60 min with a carbonation ratio of approximately 98% and a maximum CO2 sequestration of 373 kgCO2 tresidue−1. The simulated desulfurization fuel gas in the carbonation reaction had a relatively minor effect on the carbonation ratio. However, it slowed the carbonation reaction and produced a carbonation product with a smaller average particle size, which included high purity (≥99%) white calcite. This technique has the advantage of a rapid CO2 sequestration ratio, low costs, and a large potential for in situ CO2 sequestration in the electricity and steel industry. Therefore, more pilot experiments should be undertaken to provide a practical foundation for future applications.
Acknowledgements
This work was supported by the National Science Fund for Distinguished Young Scholars (51225403), the State Key Laboratory of Powder Metallurgy, Central South University, the Hunan Provincial Co-Innovation Centre for Clean and Efficient Utilization of Strategic Metal Mineral Resources, and the Fundamental Research Funds for the Central Universities of Central South University (2014zzts062).Notes and references
- C. Stewart and M.-A. Hessami, Energy Convers. Manage., 2005, 46, 403–420 CrossRef CAS PubMed.
- S. Liu and H. Yang, Appl. Clay Sci., 2014, 101, 277–281 CrossRef CAS PubMed.
- J. Jin, J. Ouyang and H. Yang, Appl. Clay Sci., 2014, 99, 246–253 CrossRef CAS PubMed.
- R. Bredesen, K. Jordal and O. Bolland, Chem. Eng. Process., 2004, 43, 1129–1158 CrossRef CAS PubMed.
- M. Mikkelsen, M. Jørgensen and F. C. Krebs, Energy Environ. Sci., 2010, 3, 43–81 CAS.
- R. Shukla, P. Ranjith, A. Haque and X. Choi, Fuel, 2010, 89, 2651–2664 CrossRef CAS PubMed.
- P. Friedlingstein, R. M. Andrew, J. Rogelj, G. P. Peters, J. G. Canadell, R. Knutti, G. Luderer, M. R. Raupach, M. Schaeffer, D. P. van Vuuren and C. Le Quéré, Nat. Geosci., 2014, 7, 709–715 CrossRef CAS PubMed.
- P. Falkowski, R. J. Scholes, E. Boyle, J. Canadell, D. Canfield, J. Elser, N. Gruber, K. Hibbard, P. Högberg, S. Linder, F. T. Mackenzie, B. Moore, T. Pedersen, Y. Rosenthal, S. Seitzinger, V. Smetacek and W. Steffen, Science, 2000, 290, 291–296 CrossRef CAS.
- A. Sanna, M. Uibu, G. Caramanna, R. Kuusik and M. M. Maroto-Valer, Chem. Soc. Rev., 2014, 43, 8049–8080 RSC.
- X. Li and H. Yang, CrystEngComm, 2014, 16, 4501–4507 RSC.
- H. E. King, O. Plümper and A. Putnis, Environ. Sci. Technol., 2010, 44, 6503–6509 CrossRef CAS PubMed.
- A.-H. A. Park and L.-S. Fan, Chem. Eng. Sci., 2004, 59, 5241–5247 CrossRef CAS PubMed.
- W. J. J. Huijgen, G.-J. Witkamp and R. N. J. Comans, Chem. Eng. Sci., 2006, 61, 4242–4251 CrossRef CAS PubMed.
- I. Stasiulaitiene, V. Vajegaite, D. Martuzevicius, G. Denafas, S. Sliaupa, J. Fagerlund and R. Zevenhoven, Environ. Prog. Sustainable Energy, 2014, 33, 512–518 CrossRef CAS PubMed.
- H. H. Khoo and R. B. H. Tan, Environ. Prog., 2006, 25, 208–217 CrossRef CAS PubMed.
- F. Mahaut, G. Gauthier, P. Gouze, L. Luquot, D. Salin and J. Martin, Environ. Prog. Sustainable Energy, 2014, 33, 572–580 CrossRef CAS PubMed.
- W. Ding, L. Fu, J. Ouyang and H. Yang, Phys. Chem. Miner., 2014, 41, 489–496 CrossRef CAS.
- W. J. J. Huijgen, R. N. J. Comans and G.-J. Witkamp, Energy Convers. Manage., 2007, 48, 1923–1935 CrossRef CAS PubMed.
- M. M. Maroto-Valer, D. J. Fauth, M. E. Kuchta, Y. Zhang and J. M. Andrésen, Fuel Process. Technol., 2005, 86, 1627–1645 CrossRef CAS PubMed.
- M. Fernández Bertos, S. J. Simons, C. D. Hills and P. J. Carey, J. Hazard. Mater., 2004, 112, 193–205 CrossRef PubMed.
- S. Teir, S. Eloneva, C.-J. Fogelholm and R. Zevenhoven, Energy, 2007, 32, 528–539 CrossRef CAS PubMed.
- J. Yu and K. Wang, Energy Fuels, 2011, 25, 5483–5492 CrossRef CAS.
- W. J. Huijgen, G. J. Witkamp and R. N. Comans, Environ. Sci. Technol., 2005, 39, 9676–9682 CrossRef CAS.
- R. Baciocchi, A. Polettini, R. Pomi, V. Prigiobbe, V. N. Von Zedwitz and A. Steinfeld, Energy Fuels, 2006, 20, 1933–1940 CrossRef CAS.
- G. P. Assima, F. Larachi, G. Beaudoin and J. Molson, Ind. Eng. Chem. Res., 2000, 51, 8726–8734 CrossRef.
- J.-H. Wee, Appl. Energy, 2013, 106, 143–151 CrossRef CAS PubMed.
- A. Iizuka, M. Fujii, A. Yamasaki and Y. Yanagisawa, Ind. Eng. Chem. Res., 2004, 43, 7880–7887 CrossRef CAS.
- S. Eloneva, S. Teir, J. Salminen, C.-J. Fogelholm and R. Zevenhoven, Energy, 2008, 33, 1461–1467 CrossRef CAS PubMed.
- L. Yan, Y. Huaifen, Z. Bo, W. Shujuan, Z. Yuqun, C. Changhe and X. Xuchang, Ecol. Environ. Sci., 2010, 19, 1682–1685 Search PubMed.
- M. G. Lee, Y. N. Jang, K. W. Ryu, W. Kim and J. H. Bang, Energy, 2012, 47, 370–377 CrossRef CAS PubMed.
- K. Song, Y.-N. Jang, W. Kim, M. G. Lee, D. Shin, J.-H. Bang, C. W. Jeon and S. C. Chae, Chem. Eng. J., 2012, 213, 251–258 CrossRef CAS PubMed.
- K. Song, Y. N. Jang, W. Kim, M. G. Lee, D. Shin, J. H. Bang, C. W. Jeon and S. C. Chae, Energy, 2014, 65, 527–532 CrossRef CAS PubMed.
- S. J. Gerdemann, W. K. O'Connor, D. C. Dahlin, L. R. Penner and H. Rush, Environ. Sci. Technol., 2007, 41, 2587–2593 CrossRef CAS.
- K. E. Kelly, G. D. Silcox, A. F. Sarofim and D. W. Pershing, Int. J. Greenhouse Gas Control, 2011, 5, 1587–1595 CrossRef CAS PubMed.
- J. H. Sharp, G. W. Brindley and B. N. Narahari Achar, J. Am. Ceram. Soc., 1966, 49, 379–382 CrossRef CAS PubMed.
- S. Tian, J. Jiang, X. Chen, F. Yan and K. Li, ChemSusChem, 2013, 6, 2348–2355 CrossRef CAS PubMed.
- J. Sun, M. F. Bertos and S. J. R. Simons, Energy Environ. Sci., 2008, 1, 370–377 CAS.
- A. K. Galwey and M. E. Brown, Thermochim. Acta, 2002, 386, 91–98 CrossRef CAS.
- M. Back, M. Kuehn, H. Stanjek and S. Peiffer, Environ. Sci. Technol., 2008, 42, 4520–4526 CrossRef CAS.
- S. C. Tian, J. G. Jiang, K. M. Li, F. Yan and X. J. Chen, RSC Adv., 2014, 4, 6858–6862 RSC.
- G. P. Assima, F. Larachi, J. Molson and G. Beaudoin, Chem. Eng. J., 2014, 245, 56–64 CrossRef CAS PubMed.
- M. Uibu, R. Kuusik, L. Andreas and K. Kirsimäe, Energy Procedia, 2011, 4, 925–932 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |





