New insights into the elasticity and multi-level relaxation of filler network with studies on the rheology of isotactic polypropylene/carbon black nanocomposite
Abstract
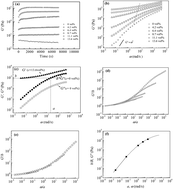
The elastic properties and multi-level relaxation behavior of a filler network in isotactic polypropylene/carbon black (iPP/CB) nanocomposites were systematically investigated, which was instructive for the development and application of viscoelastic materials. Based on a two-phase model, master curves of the elastic modulus of composites with different CB concentrations were built to describe the elastic feature of CB networks in the composites. From the elasticity of the networks, it was found that the critical volume of particle for the formation of the elastic network is 2.4 vol% and that the value of critical exponents is 5.1 ± 0.3, indicating that the particle–particle interaction in the network is strong. Based on semi-dilute fractal theory, the value obtained for the fractal dimension of the filler network was df = 2.0 ± 0.1, which was in agreement with the reaction limited aggregation mechanism, namely that CB particles must overcome a great barrier to form a cluster. The relaxation behavior of the filler network was also studied. For composites with a CB content of 2.0 vol% (slightly lower than the elastic percolation threshold of 2.4 vol%), the relaxation behavior became slower with the extension of the annealing time. Furthermore, the CB particles aggregated to form a denser network or backbone and the distribution of relaxation units became narrower, leading to an increase of the relaxation modulus. For composites with a CB content of 13.6 vol%, 0.5 h annealing treatment brought a wider distribution of relaxation units, due to the formation of “short chains” of particles, while both relaxation time and relaxation modulus of the network increased. Further annealing treatment (>0.5 h) made no difference to the distribution of relaxation units and relaxation modulus of the network, but relaxation time of the networks kept increasing. The CB concentration dependence of the relaxation behavior of the network revealed that as CB content increased, the relaxation modulus of the filler network increased monotonously. However, both relaxation time and distribution of relaxation units decreased to a minimum value when CB content increased to 6.4 vol%, and then increased with CB content.

 Please wait while we load your content...
Please wait while we load your content...