Correlating flat band and onset potentials for solar water splitting on model hematite photoanodes

Abstract

Hematite (α-Fe₂O₃) is a very promising material for solar water splitting that requires a high anodic potential to initiate the oxygen evolution reaction (OER). In this work, we explore the correlation between the downshift in flat band potential of hematite, V_fb, and in onset potential of OER, V_onset, caused by prolonged annealing. We observed a cathodic shift (i.e., towards lower potentials) of 200 mV of V_onset on model photoanodes consisting of ultra-thin hematite films, upon increasing the oxidation time during fabrication and without any further modifications. Detailed physical characterization, electrochemical impedance spectroscopy, and Mott–Schottky analysis revealed a quantitative correlation between the cathodic shift of V_onset and a lowering of V_fb. We identified a reduction in concentration of grain boundaries with increasing oxidation time, as the mechanism behind the observed shift of the V_fb. The approach presented here can be seen as a complementary strategy to co-catalysts and other post-fabrication treatments to lower V_onset. Moreover, it is generically applicable to photoelectrodes used to carry out oxidation and reduction half–cell reactions.

---

Introduction

Solar radiation is a sustainable energy source whose potential greatly exceeds the current global energy demand. However, as the Sun does not shine continuously everywhere on Earth, developing efficient and economically viable methods to concentrate and store the harvested radiation is required. An appealing possibility is to store solar energy in the form of chemical bonds, in a similar fashion to natural photosynthesis, via photoelectrochemical (PEC) water splitting.^1,2 A key factor for a commercially successful introduction of PEC water splitting is the development of photoelectrodes that meet strict requirements in terms of efficiency, durability, and availability.³

Among the 200+ compounds tested for water splitting after the seminal work by Fujishima and Honda,^4–6 hematite (α-Fe₂O₃) has emerged as a promising candidate for the water oxidation half-cell reaction (or oxygen evolution reaction, OER).^7,8 This is thanks to the following properties of hematite: (i) it has an optical bandgap energy, E_G, between 1.9 and 2.2 eV (depending on the fabrication route), appropriate to absorb a wide range of solar photon energies; (ii) it is stable under operation in neutral and alkaline conditions;⁹ and (iii) its constituents are earth-abundant and non-toxic elements.¹⁰ Based on the value of E_G alone, a maximum theoretical solar to chemical energy conversion efficiency of 16.8% has been predicted for hematite based water oxidation.¹¹ However, the efficiency values achieved hitherto are at most of about 3%.¹² This is mainly due to: (i) a low hole collection efficiency, particularly for energies close to the bandgap;¹³ and (ii) a slow OER at the hematite/electrolyte interface, hence, requiring highly anodic potentials to achieve a reasonable rate.¹⁴

The typical energetics of a junction between hematite and an aqueous electrolyte is illustrated schematically in Fig. S1a.† As the materials brought into contact reach equilibrium, electrons transfer from hematite to the electrolyte will cause an upward band bending of the conduction and valence bands in the semiconductor. By applying an external bias to the semiconductor, the extent of the band bending can be increased, decreased and even reversed to be downwards. By definition, the flat band potential, V_fb, is the electrochemical potential applied to the semiconductor that reduces this band bending to zero. Commonly found values of V_fb for hematite range between 0.4 and 0.8 V vs. the reversible hydrogen electrode (RHE).^15–18 For any potential more anodic than V_fb, the upwards band bending drives photogenerated holes towards the solid/liquid interface. Then, if the quasi-Fermi energy level of the holes E_F,p is lower than the OER potential, water oxidation can in principle take place. In practice, however, E_F,p is higher than the top of the valence band due to a notably small value of photovoltage (V_ph) sustained by hematite. Also, as mentioned above, the OER kinetics is slow. These two factors lead to the existence of a large (typically at least 400 mV) difference between V_fb and the experimentally observed V_onset. The quantity V_onset − V_fb is often referred to as overpotential for the OER.¹⁹

Fig. S1b† illustrates the present gap between the performance of state-of-the-art hematite photoanodes and those of an ideal hematite photoanode. The latter delivers a photocurrent density (per projected unit area, A_pro) j_max of 12 mA cm⁻² at an electrochemical potential equal to or lower than 0.8 V vs. RHE.²⁰ The former photoanodes, instead, show an illuminated V_onset of about 1.15 V vs. RHE and reach 4 mA cm⁻² at 1.54 V vs. RHE.²¹ Therefore, both enhancing j_max and shifting V_onset towards more cathodic potentials are needed to fully exploit the potential of hematite.

The issue of increasing j_max is typically addressed by material doping^22–24 to increase conductivity and hence improve current collection, and/or nanostructuring to increase the surface to volume ratio.^25–27 Most successful attempts to shift V_onset cathodically can be grouped into three categories:^28,29 (i) introducing OER co-catalysts, to accelerate the OER kinetics;^25,30,31 (ii) depositing under- or overlayers of other oxides, to create homo- or heterojunctions leading to reduced overpotential or to enhanced photovoltage;^32–35 (iii) post-fabrication treating the hematite surface.^36–38 The aforementioned modifications of hematite result into either an increase of the V_ph, or into a decrease of the overpotential (i.e., V_onset − V_fb). A complementary approach to further shift V_onset cathodically is to lower V_fb. This will lead to a lowered V_onset provided that worsening of other properties in the system, for instance slower OER kinetics or smaller V_ph, does not overshadow this beneficial effect. Such a strategy is rarely investigated owing to the established concept that V_fb is an intrinsic property of the semiconductor given a certain fabrication procedure. Nevertheless, combining this strategy to others of proven efficiency is likely to be required to meet the goal of 12 mA cm⁻² at 0.8 V vs. RHE, especially considering that j_max is only achieved at a potential which is 0.3–0.4 V more anodic than V_onset.

A systematic investigation of the correlation between the modification of V_fb and that of the photoelectrochemical performance of hematite photoanodes is missing in the literature, to the best of our knowledge, and we aim at correcting such deficiency in this work. Also, we address the following questions: can we shift the OER V_onset on hematite by lowering V_fb without any further post-fabrication treatments, and without affecting negatively other PEC properties of the material? And if so, can we explain the observed trend(s) regarding V_fb and V_onset? Besides the intrinsic interest in deepening the understanding of hematite based water splitting, we anticipate that lowering V_fb of hematite, combined with strategies already established to shift V_onset cathodically (and to enhance j_max), will help reaching the ideal performance of hematite photoanodes.

In order to address these questions, we employed a model system consisting of flat hematite films, and studied the impact of varying a key fabrication parameter, namely the oxidation time, on the PEC performance of the photoanodes. Our fabrication route (dry thermal oxidation of iron thin films) yields hematite photoanodes showing typical j_max between 0.1 and 0.12 mA cm⁻² (see results and discussion). This is commensurate with the j_max measured by other groups on flat hematite thin films in which the density of majority charge carriers is determined by oxygen vacancies in the lattice.^16,18,24,39 We notice that these values of current per projected unit area A_pro are more than an order of magnitude lower than those recorded on nanostructured, doped champion photoanodes. We mainly attribute such a difference to the fact that our samples are much flatter and therefore characterized by a smaller hematite/electrolyte contact area A_contact (for instance, the latter was determined to be 28 for nanocauliflower hematite fabricated by atmospheric pressure chemical vapor deposition²⁵). Moreover, we stress that we focus here on V_onset and V_fb, rather than on j_max. Our samples are an excellent model system given the focus of this work, thanks to a less complicated interpretation of PEC data – in particular from electrochemical impedance spectroscopy, EIS – as compared to that obtained on nanostructured photoelectrodes.²⁰ We present samples with a range of values of V_onset, where the lowest ones are commensurate with those measured on the best hematite photoanodes without post-fabrication treatments. We stress that it is important to analyze and understand the processes on all samples, with both high and low values of V_onset in order to make models that can be extrapolated beyond state-of-the-art.

By prolonging the oxidation time of the films, and without any further treatment, we demonstrated a cathodic shift of V_onset of about 200 mV. From EIS characterization, we obtained insights in the OER kinetics of the photoanodes and discriminated between losses taking places in the bulk of hematite and at the hematite/electrolyte interface. We used Mott–Schottky analysis to extract the V_fb in our films and thus compare the observed trends in V_onset and V_fb. Then, we employed a series of physical characterization techniques to investigate the physical mechanism(s) behind the observed PEC trends. We used scanning electron microscopy (SEM) and atomic force microscopy (AFM) to observe the morphology and topography of the hematite, respectively. We determined the oxidation state of Fe in the proximity of the hematite surface and investigated possible surface doping by means of X-ray photoemission spectroscopy (XPS). We measured the optical absorption coefficient and bandgap of hematite using optical spectroscopy. Finally, we used transmission electron microscopy (TEM) to qualitatively investigate the microstructure of hematite in terms of relative grain orientation and grain boundaries. We identified a reduction in concentration of grain boundaries upon increasing oxidation time as cause for the lowering of flat band potential.

Methods

Fabrication

Photoelectrodes were fabricated on indium tin oxide (ITO, PGO GmbH, sheet resistance ≤ 20 Ω per square) or fluorine doped tin oxide (FTO, Solaronix, sheet resistance ≤ 10 Ω per square) covered glass substrates, according to a procedure described in detail elsewhere.⁴⁰ Briefly, iron films were deposited on top of the respective substrate by physical vapor deposition (PVD 225, Kurt. J. Lesker, base pressure < 5 × 10⁻⁷ mbar). Complete conversion into Fe₂O₃ was achieved with thermal oxidation at 350 °C in a mixed N₂ : O₂ (3 : 1) atmosphere. The temperature was ramped from room temperature up to 350 °C at a rate of 15 °C min⁻¹, after which the temperature was kept constant at 350 °C for a time t_ox, which was between 0 and 24 h depending on the sample. Then, the furnace was allowed to cool down to room temperature naturally.

Characterization

SEM of the as-prepared samples was performed in a Zeiss Supra 60 VP microscope, using an acceleration voltage of 5 kV. The topography was investigated with a Bruker Dimension ICON AFM. Five 500 × 500 nm scans were acquired in tapping mode for each sample, and the roughness for each scan was calculated after image flattening using NanoScope Analysis v1.40r1 software (Bruker). The thickness of the films was measured with a Dektak 150 surface profiler (Veeco). The optical absorption in the films deposited on ITO was measured with a Cary 5000 spectrophotometer (Varian) equipped with the External Diffuse Reflectance Accessory (DRA) 2500, which accounts for optical reflection. The absorption in hematite was determined by using a blank ITO substrate as reference. The latter was exposed to the same furnace treatment as the hematite covered substrates. The absorption coefficient α was extracted from the measured absorption assuming a Lambertian absorption profile. The values obtained were used for Tauc analysis according to the formula (αhν)^0.5 = (hν − E_G), where hν is the photon energy, E_G is the bandgap energy of the semiconductor and the exponent 0.5 indicates an indirect (i.e., phonon assisted) transition. The values of E_G for different samples were obtained by extrapolating to the horizontal axis the linear part of the curves in the Tauc plots in the energy range between 2.1 and 2.3 eV. XPS spectra were acquired in a Perkin Elmer Phi 5500 setup (base pressure < 10⁻¹⁰ mbar) using Al_Kα radiation of 1.4866 keV. The XPS spectra were shifted using the C(1s) peak corresponding to adventitious carbon (284.5 eV) as a reference. TEM was performed with a field emission Jeol JEM 2100F microscope at 200 kV. To facilitate the TEM analysis, thin silicon nitride membranes (‘TEM windows’⁴¹) were used as support and hematite films were fabricated on the membranes using the same procedure as described above.

Photoelectrochemical measurements

All PEC characterization of the ITO/hematite samples was carried out in a Teflon based cell (Accent PN4300), using an Autolab PGSTAT302N potentiostat. A three electrodes configuration was used, with the ITO/hematite as working electrode, a Pt wire as counter-electrode and a Ag/AgCl (KCl saturated) reference electrode. A 0.1 M KOH solution (pH = 12.9) was used as the electrolyte, and the working electrode was illuminated from the front in all measurements. The Ag/AgCl electrode potential, V_Ag/AgCl, was converted to the reversible hydrogen electrode, V_RHE, using the equation V_RHE = V_Ag/AgCl + V⁰_Ag/AgCl + 0.059 × pH, where V⁰_Ag/AgCl = 0.197 V at 25 °C. The light source was a 300 W Xe lamp (Cermax_LX_300) equipped with a UV filter (420 nm cut-off wavelength, Schott), positioned at a distance of 38.5 cm from the PEC cell. At such a distance, the total light intensity impinging on the working electrode was estimated from product specification to be about the same as AM 1.5 filtered illumination provided by a solar simulator (100 mW cm⁻²), although with a different spectral distribution. Cyclic voltammetry was performed between 0.76 and 1.76 V vs. RHE at a scan rate of 10 mV s⁻¹. To obtain the photocurrent density j, the current was divided by the projected area in contact with the electrolyte, A_pro. Only the forward scan from cathodic to anodic potentials was plotted for ease of visualization. For the EIS measurements, the DC voltage was changed in steps of 0.1 V from 1.76 to 0.86 V vs. RHE, on top of which an AC voltage of root mean square amplitude of 10 mV and frequency varying between 10⁵ and 0.1 Hz was superimposed. Nyquist plots obtained under illumination were fitted using the software Nova v. 1.9 (Metrohm Autolab). Mott–Schottky analysis was performed in the dark, in the same potential window, using an AC voltage with a frequency of 10⁴ Hz. Cyclic voltammetry of the FTO/hematite samples was performed in the same 3-electrode configuration, using a Gamry ref. 600 potentiostat, in a H-type glass cell with working electrode and counter-electrode compartments separated by a glass frit. The working electrode compartment had flat optical windows to allow for the illumination of the samples. A solar simulator (SKU SS150, Sciencetech. Inc.) was the illumination source, with intensity at the working electrode surface adjusted to 100 mW cm⁻² using a NIST calibrated photodiode.

Results and Discussion

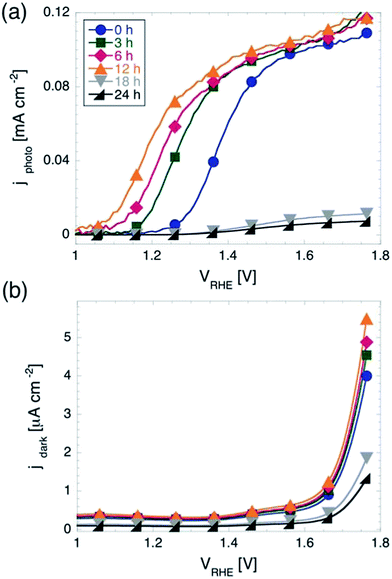
In light assisted OER from water splitting, as explained above, two quantities are of key interest, namely the onset potential V_onset and the plateau photocurrent j_max measured before purely electrochemical water splitting is observed. Fig. 1 shows the results of the cyclic voltammetry measurements performed on samples with different t_ox under illumination and in the dark. While samples with t_ox between 0 and 12 h show a maximum photocurrent between 0.11 and 0.12 mA cm⁻², those with longer t_ox show negligible photoactivity. This is most likely due to the loss of electrical conductivity of ITO when exposed at temperatures of 350 °C for prolonged times.⁴² Therefore, in the remainder of the manuscript we will focus on samples with t_ox ≤ 12 h.

Fig. 1 Current density j as function of electrochemical potential V for hematite films on ITO. (a) Photocurrent density under UV-filtered illumination from a Xe-lamp. The onset potential for the OER V_onset shifts of 200 mV towards more cathodic potentials for t_ox increasing from 0 to 12 h. For longer t_ox, the films show negligible photoactivity. (b) Current density measured in the dark. The onset potential shifts only by around 30 mV between t_ox = 0 h and t_ox = 12 h.

The maximum photocurrent j_max does not depend significantly on t_ox for potentials more anodic than 1.6 V vs. RHE. As discussed in the introduction, the values j_max measured here are more than an order of magnitude lower than those measured on state-of-the-art photoanodes, however commensurate to those observed on photoanodes fabricated using similar routes.³⁹ It is worth mentioning that we found an increase of j_max of about 20% as compared to hematite films fabricated via the same procedure and characterized in previous work.⁴³ This difference is most likely caused by the differences in the spectral distribution of the illumination source. We recall that here the light intensity impinging on the sample was 100 mW cm⁻², but not with an AM 1.5 spectral distribution.

Although all samples shown in Fig. 1a reach very similar values of j_max for high anodic potentials, they show a striking difference in V_onset, which moves towards more cathodic potentials for increasing t_ox. Considering the quantitative determination of V_onset, different definitions can be found in the literature. For example, V_onset has been defined as: (i) the potential at which the photocurrent exceeds a certain defined value,³⁰ (ii) the potential at which dJ/dV exceeds a certain defined value,⁴⁴ or (iii) the potential at which the tangent to the J(V) curve in the region of maximum slope intersects the J(V) curve measured in the dark.³³ It should be noted that all these definitions are somewhat arbitrary and may be more or less appropriate depending on the shape of the J(V) curves at hand. For instance, using method (iii) can result in a situation where a curve with a steep slope will have a more anodic V_onset than one with a flatter slope, although they may have the same V_onset according to methods (i) and/or (ii). We note that the J(V) curves presented here show a very similar slope after the photocurrent starts rising. Therefore, although the choice of method to define V_onset might slightly affect the exact values extracted from the J(V) curves, the shifts in V_onset with varying t_ox will be practically be independent of the chosen method. Here we used method (i), with 10 μA cm⁻² as a threshold in photocurrent density (corresponding to about 10% of j_max). According to this definition, we found V_onset to be equal to 1.28 V vs. RHE for t_ox = 0. Upon increasing t_ox from to 3, 6, and 12 hours, V_onset shifts significantly towards more cathodic potentials, to 1.19, 1.13, and 1.08 V vs. RHE, respectively.

The onset potential showed a much weaker dependency on t_ox for cyclic voltammetry in the dark, as shown in Fig. 1b. Using method (i) again (with threshold current corresponding to 10% of the maximum current observed in the dark in the potential window investigated), we found that the onset potential shifts only 30 mV in total when increasing t_ox from 0 to 12 h. This indicates that the effect of prolonging t_ox on the OER in the dark is negligible.

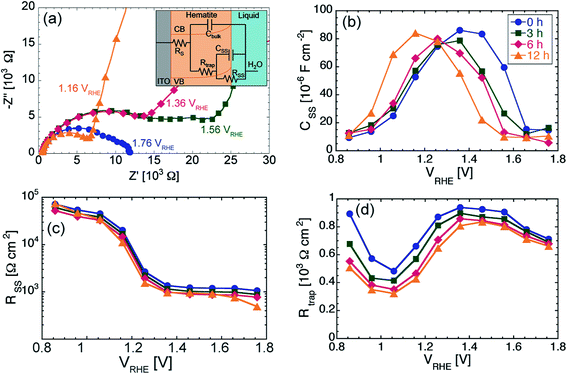
We further investigated the PEC properties of the photoanodes via EIS. Recent studies have established EIS as a powerful technique to characterize the dynamics of charge transfer at the hematite/electrolyte interface, as well as of charge transport in the bulk of the semiconductor.^14,45 Data from EIS measurements is often shown in form of Nyquist plots, where the real component and negative imaginary component of the complex impedance Z are plotted on the horizontal and vertical axis, respectively. Fig. 2a shows the Nyquist plots obtained for the 6 h sample, under illumination, at some relevant values of DC bias. A qualitative decrease in total impedance is visible with increasing potential (at 1.16 V vs. RHE the impedance values at lower frequencies are well outside the range of impedance in the plot). The presence of two semicircles indicates that two time constants are present in the system. We found the same evolution of the Nyquist plots for increasingly anodic potential for all samples measured.

Fig. 2 (a) Representative Nyquist plots obtained from EIS measurements on the t_ox = 6 h sample under illumination at different applied potential. Inset: equivalent circuit used to fit the Nyquist plots under illumination. (b–d) Results from the equivalent circuit fitting of the Nyquist plots. The following quantities are plotted as function of applied potential: (b) Surface states capacitance C_SS, (c) Charge transfer resistance R_SS, (d) trapping resistance R_trap.

In order to correlate changes in the Nyquist plots with changes in the properties of charge transport through the photoanode and of charge transfer at the hematite/semiconductor interface, equivalent circuit modeling is required. For photoelectrodes where water oxidation performance is hampered by slow OER kinetics, an appropriate circuit is shown in the inset of Fig. 2a, which has been discussed and employed previously for studying hematite photoanodes.^8,45 In brief, the electrical components of this equivalent circuit are: R_S, the contact resistance between ITO and hematite; C_bulk, the capacitance originating from the charge in the space-charge layer in hematite; R_trap, the resistance associated with transport of charge through the bulk of hematite; C_SS, the chemical capacitance associated with surface states at the hematite/electrolyte interface,⁴⁶ and R_SS, the resistance associated with charge transfer from hematite to the electrolyte. Within this model, the high and low frequency semicircles in the Nyquist plots are associated with bulk and surface properties of the photoanode, respectively. It is clear that the impedance associated with the low frequency semicircle decrease considerably with increasing potential, while the impedance associated with high frequency is basically independent of the applied bias.

By fitting of the Nyquist plots using the equivalent circuit described above, we extracted the values of C_SS, R_trap and R_SS for all samples as function of the applied DC potential. The results are shown in Fig. 2b–d. For each sample, C_SS(V) first increases for more anodic potential, reaches a maximum and then decreases back to about its initial value for the most anodic potentials. Moreover, the potential at which C_SS(V) peaks is close to the onset potential V_onset. This fact is a signature that the OER under illumination takes place via surface states for potential values close to V_onset. These surface states are first charged and then discharged when the potential is sufficiently anodic to start the OER. We estimated the charge density on the surface state Q_SS by integrating C_SS with respect to V. We found Q_SS to be between 38.2 and 39.2 μC cm⁻² for the 12 h and 0 h samples, respectively. In other words Q_SS is basically constant regardless of t_ox. These observations, together with the weak dependency of the dark electrolysis onset potential on t_ox, point to very similar OER kinetics for all samples.

The hematite/electrolyte charge transfer resistance, R_SS(V), is plotted in Fig. 2c, from which we see that the transfer of holes from the semiconductor to the electrolyte is not significantly affected by changing t_ox. Fig. 2d shows that the resistance associated with recombination of charge carriers in the bulk of the hematite, R_trap(V), has a similar behavior for all samples, with a minimum at 1.06 V vs. RHE and a flatter region for potentials more anodic than 1.36 V vs. RHE. However, the values of R_trap are clearly decreasing for increasing t_ox, with the strongest effect for potentials more cathodic than 1.56 V vs. RHE.

We can summarize the main findings of our equivalent circuit analysis as follows: (1) the results from the analysis of the C_SS(V) and R_SS(V) plots are additional evidence that varying t_ox does not affect the OER kinetics under illumination; (2) the decrease of R_trap(V) with increasing t_ox for low anodic bias indicates a possible beneficial effect of prolonged oxidation time on the charge carrier transport within the films.

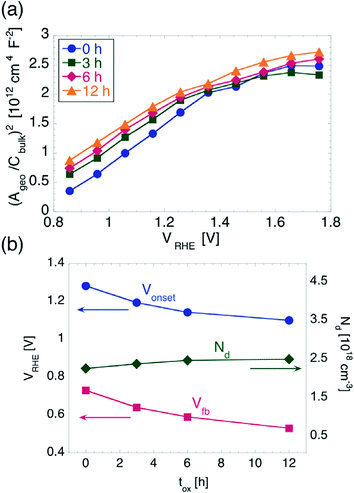
Mott–Schottky (MS) analysis is commonly performed in the dark, in order to extract not only V_fb, but also the donor/acceptor (for n- and p-type semiconductor, respectively) concentration, N_D. For a perfectly planar semiconductor–electrolyte interface (i.e. where A_pro = A_contact), the MS equation reads (A_pro/C_bulk)² = 2(V − V_fb − k_bT/e)/(ε₀ε_rN_D), where, C_bulk is the capacitance of the space-charge layer, k_b is the Boltzmann constant, T is the absolute temperature, e is the elementary charge, ε₀ is the permittivity of vacuum and ε_r is the relative permittivity of the semiconductor.⁴⁷ The validity of this simple relationship between C_bulk and V − V_fb lies on the following assumptions: (i) C_bulk is much smaller than the capacitance C_H associated with the Helmholtz layer in the electrolyte; (ii) the donors/acceptors are uniformly distributed in space, have all the same energy, and are all ionized; (iii) the width of the space-charge layer W_SC is much smaller than the thickness d of the semiconductor. Under these assumptions, the MS plot is linear, and N_D can be obtained from the relationship N_D = 2/ε₀ε_reS, where S is the slope of the plot, while V_fb is obtained from the intercept with the horizontal axis.

The MS plots for the values of t_ox investigated in this work are indeed linear for potentials between 0.86 and 1.36 V vs. RHE, as shown in Fig. 3a, while for potentials more anodic they show a concave shape. The latter could in principle be explained by assuming a special non-uniform distribution of ionized donors.⁴⁸ In particular, one would have to assume a continuously increasing N_D with increasing distance from the hematite/electrolyte interface. However, we do not consider such a possibility as plausible, since the oxidation of Fe into Fe₂O₃ is carried out for a sufficiently long time (including ramp up and cool down time) for the resulting films to have uniform electronic properties throughout their thickness.

Fig. 3 (a) Mott–Schottky plots for hematite films on ITO. (b) Onset potential V_onset and flat band potential in hematite V_fb (left y-axis) and donor concentration N_D (right y-axis) as function of t_ox.

Instead, the considerably small thickness of our hematite films makes the approximation W_SC ≪ d questionable. It has been shown that, in photoanodes consisting of a thin TiO₂ deposited on ITO, the depletion region can extend into the ITO for sufficiently high anodic potentials, and the MS equation needs to be modified to take this effect into account.⁴⁹ In particular, the MS plot was predicted to have two distinct slopes, one at more cathodic potentials, which is determined by the ε_r and N_D of the TiO₂, and one for more anodic potentials, which is determined by the ε_r and N_D of the ITO. The potential V_th where the slope changes is the potential at which W_SC in the TiO₂ equals the TiO₂ thickness. The following relationship between d and V_th was then found: d = ε₀ε_rS^0.5(V_th − V kT/e)^0.5. We followed a similar approach to further analyze our MS plots. We note that the potentials applied here were not so anodic that the second slope could be determined without a large deviation. Therefore we used, for the slope at high anodic potentials, the values of ε_r (ITO) = 9 and N_D (ITO) = 10²⁰ cm⁻³, which are normally found for ITO films with similar sheet resistance as compared to the ones used here.^49,50 Once V_th is determined and d is known, ε_r can be extracted. We found that ε_r only varies between 18.9 and 19 when increasing t_ox. We note that these values for ε_r are considerably smaller than the values of 32 and 80 often plugged into the simplest form of the MS equation to directly extract N_D.^28,51 Within the approach used here, instead, we can use the ε_r extracted from our MS plots to obtain N_D. We found the latter to increase from 2.28 × 10¹⁸ cm⁻³ to 2.52 × 10¹⁸ cm⁻³ with t_ox increasing from 0 to 12 h. From the measurements performed here we cannot determine unambiguously the origin of such difference in N_D. Nevertheless, we stress that the increase of N_D is only of a factor of 1.1, which we judge insufficient to explain the considerable V_onset shift found from cyclic voltammetry. Moreover, we found a quantitative correlation between the shift of V_onset and that of V_fb, as explained below.

In order to evaluate V_fb, we fitted the linear part of the MS plots, where only the properties of hematite come into play. Since we did not measure directly A_contact, we used the value of A_pro (0.1 cm²) as contact area for all samples, and we found V_fb to shift from 0.73 V to 0.53 V vs. RHE. Such a shift towards more negative potentials follows closely the shift of V_onset observed during the cyclic voltammetry measurements, as illustrated in Fig. 3b. The difference between V_onset and V_fb is about 550 mV irrespective of t_ox, which points once again to very similar OER kinetics for all samples. This is in contrast to the reduction in V_onset obtained upon employing electrocatalysts or other surface coatings, which do not change V_fb appreciably.^30,52 The shift of V_fb could in principle be caused by a decrease in the Helmholtz layer capacitance. A treatment of the solid/liquid interface that includes explicitly C_H has shown to predict a MS plot with the same slope as in the simplest case,⁵³ but with an intercept shifted by an amount equal to ε₀ε_reN_D/2C_H² = 1/S C_H². In order to obtain the extracted 200 mV shift of V_fb, one would have to assume an increase of C_H of a factor of 25 upon increasing t_ox from 0 to 12 h, which we judge unreasonable given the similarity of the hematite/electrolyte interface properties as extracted by EIS under illumination.

Another possible mechanism of the observed shift of V_fb could be the introduction of In or Sn atoms from ITO into the hematite, which would be consistent with the slight increase of N_D extracted previously. The modification of V_fb upon doping has been observed, for instance, in other semiconductors used in PEC cells/solar cells.^54,55 However, direct evidence that neither In nor Sn did not diffuse from ITO to the surface of the photoanodes is offered by XPS measurements, as discussed further on. Furthermore, we performed control cyclic voltammetry measurements on hematite samples deposited FTO, which is known to be thermally stable up to 700 °C. The photocurrent measurements carried out on the FTO based films demonstrated a similar cathodic shift of the onset potential upon increasing t_ox from 3 to 12 h to that obtained for the films deposited on ITO, which confirms that the observed V_onset is also independent of the electron collection layer underneath hematite.

Thanks to the MS analysis, we established a quantitative correlation between the extracted shift of V_fb and the shift of V_onset observed during the cyclic voltammetry measurements. While V_fb is typically determined by the properties of the solid/liquid junction and of the space-charge layer, V_onset is determined by the properties of the whole photoelectrode. However, due to the very small thickness of the films used here, it is reasonable to consider both V_fb and V_onset as determined by the properties of the whole film. Nevertheless, it is not clear at this stage if the shift of V_fb is correlated to any change in the physical properties of the hematite films, which we characterized in deeper detail.

We measured the hematite thickness by surface profiler, and found it to be 25 ± 2 nm irrespective of t_ox. SEM inspection did not indicate an obvious difference in morphology between the samples, as shown in Fig. S2.† Investigation by AFM led to the conclusion that the topography of the samples is not affected appreciably by prolonging t_ox, as shown in Fig. S3.† The root mean square roughness, R_q, was found to vary only very slightly from 2.3 ± 0.15 nm for t_ox = 0 h to 2.32 ± 0.18 nm for t_ox = 12 h, which justifies the use of the same value of contact area for all the samples.

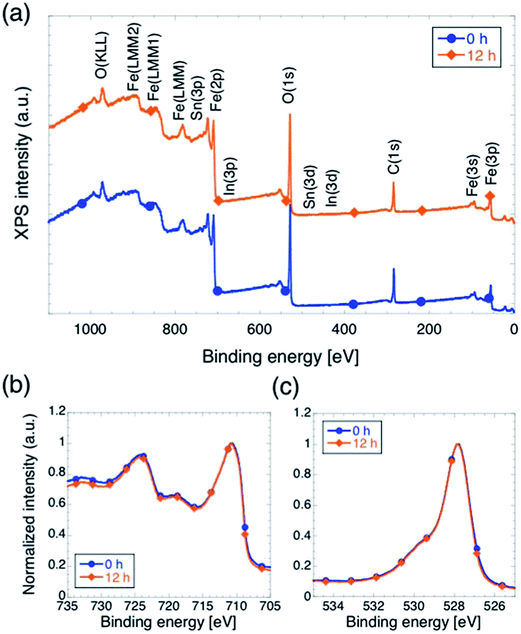
We carried out XPS measurements on sample with t_ox equal to 0 and 12, in order to perform analysis of chemical composition and electronic states of the surface of the films, and the results are summarized in Fig. 4. First, we notice that no peaks appear in the survey scans (panel a) at energies corresponding to peaks indicating the presence of In or Sn, which is a further, direct confirmation that neither In nor Sn did not diffuse up to the hematite surface. Second, the normalized XPS Fe(2p) and O(1s) signals (panels b and c respectively) are practically identical in shape, indicating that surface composition of the sample and oxidation state of the iron within a few nm from the surface are not affected by changing t_ox.

Fig. 4 XPS characterization for hematite films on ITO with t_ox = 0 h and t_ox = 12 h. (a) Survey scans with peaks identification. The curves are shifted on the vertical axis for ease of visualization. Clearly, no In or Sn is detected. (b). Normalized intensity profiles of Fe(2p) peaks. (c) Normalized intensity profiles of O(1s) peaks.

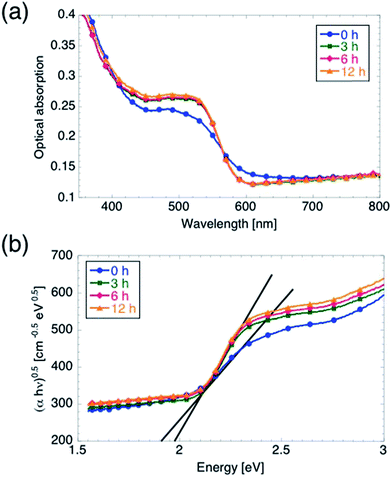
We characterized the optical properties of the films using spectrophotometry, and the results are summarized in Fig. 5. It is worth mentioning that the use of the integrating sphere accessory to perform these measurements enabled us to directly measure the sum of scattered (including reflected) light and transmitted light, from which we obtained the absorption Abs = 1 − (Sca + Tr). The onset of optical absorption between 630 and 600 nm indicates that the oxidation process is complete even for t_ox = 0 h, i.e. when ramping up the temperature to 350 °C and starting the cool-down immediately afterwards. The absorption profile of the 0 h sample, however, differs slightly from the other spectra. In particular, the absorption is lower for wavelengths between 420 and 560 nm, whereas it is slightly higher between 560 and 640 nm. Inspection of the Tauc plots in Fig. 5b reveals that E_G increases from 1.9 to 1.98 eV upon increasing t_ox from 0 to 3 hours, while further increasing t_ox leaves E_G unmodified. We believe, however, that the observed discrepancy in optical absorption between the 0 h samples and the other samples cannot account for the observed difference in V_onset, for the following reasons. First, an increase in number of absorbed photons (with no other changes in the electrochemical properties of the film) should lead to an increased j_max rather than a shift in V_onset.¹⁵ Second, the optical absorption is not affected by further increasing t_ox from 3 hours to 6 or 12 hours, although V_onset is shifted further cathodically. On the other hand, the slightly lower value of j_max measured on the 0 h sample as compared to the other samples (for which j_max is the same within a 5% margin) can be attributed to the lower optical absorption between 420 and 560 nm observed for the 0 h sample.

Fig. 5 Optical characterization of hematite films. (a) Optical absorption as function of wavelength. (b) Bandgap energy determination from Tauc analysis performed assuming an indirect bandgap in hematite. The bandgap energy E_G increases from 1.90 to 1.98 eV between the 0 h sample and the other samples.

Complete conversion of Fe into hematite was confirmed in a previous work⁵⁶ by XRD measurements performed on samples at least 4 times thicker than those used here. It is thus reasonable to assume than the same holds for the ultra-thin films employed in this study. In spite of several attempts, we did not manage to obtain significant XRD data on these 25 nm thick films. Therefore, we resorted to TEM characterization in order to investigate the properties of the films in terms of crystallinity and grain boundaries. The results are summarized in Fig. 6. While all the films are polycrystalline as expected, we did observe clear changes in the sample at the nanoscale. In particular, the crystallite size increases distinctly with increasing t_ox. For the lowest t_ox, the average crystallite size is of the order of 10 nm or smaller. Since the film thickness is 25 nm there are several crystallites in the TEM field of view, which makes it somewhat difficult to interpret the images and in particular to perform quantitative analysis of the crystallite size distribution. Nonetheless, it is qualitatively clear that the crystallites grow with increasing t_ox. For example, panel (d) (t_ox = 12 h) shows crystallites that are significantly larger in size than the film thickness (several tens of nm).

Fig. 6 TEM images of hematite films with t_ox = 0 h (a), 3 h (b), 6 h (c) and 12 h (d). Panels (b) and (d) also include insets showing high resolution images.

In view of the information obtained from the TEM analysis, we propose the following qualitative explanation for the shift of V_fb, and therefore of V_onset. The increase of grain size for increasing t_ox determines a decrease in density of grain boundaries in hematite. These grain boundaries are typically associated with potential drops that reduce the efficiency of charge transport within the film.²¹ Therefore, by reducing the density of grain boundaries we also reduce the extent of the potential drops that are detrimental for the charge transport within hematite. In other words, a stronger band bending in hematite is obtained by increasing t_ox. As a consequence, a larger potential is needed in order to reach the condition of zero band bending in hematite, which is V_fb by definition. Therefore, V_fb shifts towards lower, or towards more cathodic potentials. We observe that such mechanism is consistent with all data extracted from the EIS measurements, in particular with the decrease in bulk trapping resistance R_trap recorded under illumination. Moreover, we highlight that the proposed mechanism for the shift of V_fb, and thus of V_onset, is consistent with the similar values of j_max measured at highly anodic applied potentials. In this regime, in fact, the mechanism limiting the photocurrent in hematite photoanodes is the number of photons absorbed, rather than the charge transport within the film or the OER kinetics at the surface.¹⁵

Conclusions

In conclusion, in this work we systematically studied the correlation between the OER V_onset and V_fb of hematite based photoelectrodes. We addressed the question if the OER onset potential V_onset on hematite can be lowered by lowering the flat band potential V_fb of the material, and if this can be achieved without post-fabrication treatments. To this end, we employed a model system based on hematite ultra-thin films, and we determined how V_onset and V_fb are affected by the oxidation time during fabrication of the photoanodes. We demonstrated a cathodic shift of V_onset of 200 mV on increasing t_ox from 0 to 12 hours, without any further surface treatment. A combination of AFM, XPS characterization and EIS measurements under illumination indicated that increasing t_ox did not affect the electrochemical properties of the hematite/electrolyte interface. EIS also pointed to increased charge transport efficiency within hematite for prolonged t_ox. Mott–Schottky analysis revealed a quantitative correlation between the cathodic shift of V_onset and a shift of V_fb in the same direction. The fact that the difference between V_onset and V_fb is independent of t_ox offered further confirmation that varying the oxidation time did not affect the kinetics of the OER. From TEM analysis we proposed that the mechanism responsible for the shift of V_fb hematite, and therefore for the shift of the OER V_onset, is the improved quality of the films in terms of increased grain size and thus of reduced density of grain boundaries, leading to an increase in band bending in the semiconductor. The results presented here point at the possibility of enhancing the performance of hematite in terms of lowering V_onset by improving the intrinsic properties of the semiconductor, which we expect to be compatible with further strategies towards the same goal such as introduction of underlayers, addition of electrocatalysts, or other surface coatings and post-fabrication treatments. Furthermore, the concepts presented in the Introduction regarding the energetics of a semiconductor/electrolyte interface can be applied not only to hematite, but much more generically to both n-type and p-type semiconductors. Therefore, the approach of shifting V_fb can readily be applied to any semiconductor-based photoelectrodes, i.e. not only lowering V_fb for n-type semiconductors used in oxidation half-cell reactions, but also increasing V_fb for p-type semiconductors employed for reduction half-cell reactions.

Acknowledgements

BI, BW, and IZ thank Formas (project numbers 219-2011-959 and 229-2009-772) for financial support. AH acknowledges support from the Swedish Research Council. BI thanks the Areas of Advance for Material Science and for Nanotechnology at Chalmers University of Technology supporting his external research stay at UNSW. Dr. Yunhau Ng and Prof. Rose Amal from the School of Chemical Engineering (UNSW) are gratefully acknowledged for providing the potentiostat for the PEC measurements performed at UNSW. GC and HZ acknowledge support from the Australian Government through the Australian Renewable Energy Agency (ARENA). The Australian Government, through ARENA, is supporting Australian research and development in solar photovoltaic and solar thermal technologies to help solar power become cost competitive with other energy sources. The views expressed herein are not necessarily the views of the Australian Government, and the Australian Government does not accept responsibility for any information or advice contained herein.

References

1. M. Grätzel, Nature, 2001, 414, 338–344.
2. Y. Tachibana, L. Vayssieres and J. R. Durrant, Nat. Photonics, 2012, 6, 511–518.
3. T. Bak, J. Nowotny, M. Rekas and C. C. Sorrell, Int. J. Hydrogen Energy, 2010, 27, 991–1022.
4. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
5. M. D. Hernández-Alonso, F. Fresno, S. Suárez and J. M. Coronado, Energy Environ. Sci., 2009, 2, 1231.
6. F. E. Osterloh, Chem. Mater., 2008, 20, 35–54.
7. Z. Li, W. Luo, M. Zhang, J. Feng and Z. Zou, Energy Environ. Sci., 2013, 6, 347.
8. B. Iandolo and A. Hellman, Angew. Chem., Int. Ed. Engl., 2014, 53, 13404–13408.
9. L. R. Yeh and N. Hackerman, J. Electrochem. Soc., 1977, 124, 833.
10. P. C. K. Vesborg and T. F. Jaramillo, RSC Adv., 2012, 2, 7933.
11. A. Murphy, P. Barnes, L. Randeniya, I. Plumb, I. Grey, M. Horne and J. Glasscock, Int. J. Hydrogen Energy, 2006, 31, 1999–2017.
12. J. Brillet, J. Yum, M. Cornuz, T. Hisatomi, R. Solarska, J. Augustynski, M. Graetzel and K. Sivula, Nat. Photonics, 2012, 6, 824–828.
13. L. A. Marusak, R. Messier and W. B. White, J. Phys. Chem. Solids, 1980, 41, 981–984.
14. L. M. Peter, J. Solid State Electrochem., 2012, 17, 315–326.
15. H. Dotan, K. Sivula, M. Grätzel, A. Rothschild and S. C. Warren, Energy Environ. Sci., 2011, 4, 958.
16. A. P. Singh, A. Mettenbörger, P. Golus and S. Mathur, Int. J. Hydrogen Energy, 2012, 37, 13983–13988.
17. G. Rahman and O.-S. Joo, Int. J. Hydrogen Energy, 2012, 37, 13989–13997.
18. R. Franking, L. Li, M. A. Lukowski, F. Meng, Y. Tan, R. J. Hamers and S. Jin, Energy Environ. Sci., 2013, 6, 500.
19. M. Barroso, S. R. Pendlebury, A. J. Cowan and J. R. Durrant, Chem. Sci., 2013, 4, 2724.
20. Photoelectrochemical Hydrogen Production, ed. R. van de Krol and M. Grätzel, Springer US, Boston, MA, 2012, vol. 102.
21. S. C. Warren, K. Voïtchovsky, H. Dotan, C. M. Leroy, M. Cornuz, F. Stellacci, C. Hébert, A. Rothschild and M. Grätzel, Nat. Mater., 2013, 12, 842–849.
22. I. Cesar, K. Sivula and A. Kay, J. Phys. Chem. C, 2008, 772–782.
23. A. Kleiman-Shwarsctein, Y.-S. Hu, A. J. Forman, G. D. Stucky and E. W. McFarland, J. Phys. Chem. C, 2008, 112, 15900–15907.
24. S. Kumari, A. P. Singh, D. Deva, R. Shrivastav, S. Dass and V. R. Satsangi, Int. J. Hydrogen Energy, 2010, 35, 3985–3990.
25. A. Kay, I. Cesar and M. Graetzel, J. Am. Chem. Soc., 2006, 15714–15721.
26. Y. Lin, S. Zhou, S. W. Sheehan and D. Wang, J. Am. Chem. Soc., 2011, 133, 2398–2401.
27. A. Mao, G. Y. Han and J. H. Park, J. Mater. Chem., 2010, 20, 2247.
28. K. Sivula, F. Le Formal and M. Grätzel, ChemSusChem, 2011, 4, 432–449.
29. M. J. Katz, S. C. Riha, N. C. Jeong, A. B. F. Martinson, O. K. Farha and J. T. Hupp, Coord. Chem. Rev., 2012, 256, 2521–2529.
30. L. Badia-Bou, E. Mas-Marza, P. Rodenas, E. M. Barea, F. Fabregat-Santiago, S. Gimenez, E. Peris and J. Bisquert, J. Phys. Chem. C, 2013, 117, 3826–3833.
31. S. D. Tilley, M. Cornuz, K. Sivula and M. Grätzel, Angew. Chem., 2010, 122, 6549–6552.
32. F. Le Formal, K. Sivula and M. Grätzel, J. Phys. Chem. C, 2012, 116, 26707–26720.
33. F. Le Formal, N. Tétreault, M. Cornuz, T. Moehl, M. Grätzel and K. Sivula, Chem. Sci., 2011, 2, 737.
34. T. Hisatomi, F. Le Formal, M. Cornuz, J. Brillet, N. Tétreault, K. Sivula and M. Grätzel, Energy Environ. Sci., 2011, 4, 2512.
35. T. Hisatomi, H. Dotan, M. Stefik, K. Sivula, A. Rothschild, M. Grätzel and N. Mathews, Adv. Mater., 2012, 24, 2699–2702.
36. Y.-S. Hu, A. Kleiman-Shwarsctein, G. D. Stucky and E. W. McFarland, Chem. Commun., 2009, 2652–2654.
37. M. Zhang, W. Luo, N. Zhang, Z. Li, T. Yu and Z. Zou, Electrochem. Commun., 2012, 23, 41–43.
38. D. Cao, W. Luo, J. Feng, X. Zhao, Z. Li and Z. Zou, Energy Environ. Sci., 2014, 7, 752–759.
39. P. Hiralal, S. Saremi-Yarahmadi, B. C. Bayer, H. Wang, S. Hofmann, K. G. Upul Wijayantha and G. A. J. Amaratunga, Sol. Energy Mater. Sol. Cells, 2011, 95, 1819–1825.
40. B. Iandolo, T. J. Antosiewicz, A. Hellman and I. Zorić, Phys. Chem. Chem. Phys., 2013, 15, 4947–4954.
41. A. W. Grant, Q.-H. Hu and B. Kasemo, Nanotechnology, 2004, 15, 1175–1181.
42. R. Synowicki, Thin Solid Films, 1998, 313–314, 394–397.
43. B. Iandolo, B. Wickman, B. Seger, I. Chorkendorff, I. Zorić and A. Hellman, Phys. Chem. Chem. Phys., 2014, 16, 1271–1275.
44. F. Le Formal, M. Grätzel and K. Sivula, Adv. Funct. Mater., 2010, 20, 1099–1107.
45. B. Klahr, S. Gimenez, F. Fabregat-Santiago, T. Hamann and J. Bisquert, J. Am. Chem. Soc., 2012, 134, 4294–4302.
46. J. Bisquert, Phys. Chem. Chem. Phys., 2008, 10, 49–72.
47. Z. Chen, H. N. Dinh and E. Miller, Photoelectrochemical Water Splitting, Springer, New York, NY, 2013.
48. J. Schoonman, J. Electrochem. Soc., 1981, 128, 1154.
49. R. van de Krol, J. Electrochem. Soc., 1997, 144, 1723.
50. J. E. A. M. van den Meerakker, E. A. Meulenkamp and M. Scholten, J. Appl. Phys., 1993, 74, 3282.
51. J. A. Glasscock, P. R. F. Barnes, I. C. Plumb and N. Savvides, J. Phys. Chem. C, 2007, 111, 16477–16488.
52. B. Klahr, S. Gimenez, F. Fabregat-Santiago, J. Bisquert and T. W. Hamann, J. Am. Chem. Soc., 2012, 134, 16693–16700.
53. M. Tomkiewicz, J. Electrochem. Soc., 1979, 126, 1505.
54. M. Radecka, K. Zakrzewska, M. Wierzbicka, A. Gorzkowska and S. Komornicki, Solid State Ionics, 2003, 157, 379–386.
55. R. Beranek and H. Kisch, Electrochem. Commun., 2007, 9, 761–766.
56. B. Iandolo and M. Zäch, Aust. J. Chem., 2012, 65, 633.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra10215d

‡ Current address: Center for Electron Nanoscopy, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark.

---