Understanding the thermal dehydrochlorination reaction of 1-chlorohexane. Revealing the driving bonding pattern at the planar catalytic reaction center†
Abstract
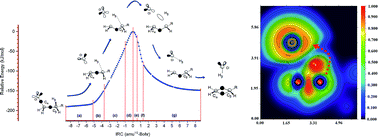
The nature of bonding along the gas-phase thermal decomposition of 1-chlorohexane to produce 1-hexene and hydrogen chloride has been examined at the DFT M05-2X/6-311+G(d,p) level of theory. Based on results both from energetical and topological analysis of the electron localization function (ELF), we propose to rationalize the experimental available results not in terms of a decomposition via a four-membered cyclic transition structure (TS), but properly as a two stage one step reaction mechanism featuring a slightly asynchronous process associated to the catalytic planar reaction center at the TS. In this context, the first electronic stage corresponds to the Cδ+⋯Clδ− bond cleavage, which take place on the activation path earlier the transition structure be reached. There is no evidence of a Cl–C bond at the TS configuration. The second stage, associated to the top of the energy barrier, includes the TS and extends beyond on the deactivation pathway towards the products. The existence of both bonding and nonbonding non covalent interactions (NCI) are also revealed for the first time for the TS configuration.

 Please wait while we load your content...
Please wait while we load your content...